Should we do research on alignment schemes which use RLHF as a building block? E.g. work on recursive oversight schemes or RLHF with adversarial training?
- IMO, this kind of research is promising and I expect a large fraction of the best alignment research to look like this.
This seems like the key! It’s probably what people actually mean by the question “is RLHF a promising alignment strategy?”
Most of this post is laying out thoughtful reasoning about related but relatively uncontroversial questions like “is RLHF, narrowly construed, plausibly sufficient for alignment” (of course not) and “is RLHF, very broadly construed, plausibly useful for alignment” (of course yes). I don’t want to diminish the value of having those answers be more common-knowledge. But I do want to call attention to how little of the reasoning elsewhere in the post seems to me to support the plausibility of this opinion here, which is the most controversial and decision-relevant one, and which is stated without any direct justification. (There’s a little bit of justification for it elsewhere, which I’ve argued against in separate comments.) I’m afraid that one post which states a bunch of opinions about related questions, while including detailed reasoning but only for the less controversial ones, might be more persuasive than it ought to be about the juicier questions.
I’m afraid that one post which states a bunch of opinions about related questions, while including detailed reasoning but only for the less controversial ones, might be more persuasive than it ought to be about the juicier questions.
It isn't my intention to do this kind of motte and bailey; as I said, I think people really do conflate these questions, and I think that the things I said in response to some of these other questions are actually controversial to some. Hopefully people don't come away confused in the way you describe.
I don’t think RLHF seems worse than [prompting or filtering to] try to get your model to use its capabilities to be helpful. (Many LessWrong commenters disagree with me here but I haven’t heard them give any arguments that I find compelling.)
Where does the following argument fall flat for you?
- Human feedback is systematically wrong, e.g. approving of impressively well-reasoned-looking confabulations much more than “I don’t know.”
- The bias induced by sequence prediction preserves some of the correlations found in Internet text between features that human raters use as proxies (like being impressively well-reasoned-looking) and features that those are proxies for (like being internally coherent, and being consistent with other information found in the corpus).
- RL fine-tuning applies optimisation pressure to break these correlations in favor of optimising the proxies.
- Filtering (post-sequence-generation) preserves the correlations while optimising, making it more likely that the outputs which pass the filter have the underlying features humans thought they were selecting for.
Thanks for the clear argument (and all your other great comments).
I totally agree with 1 and 2. I'm not sure what I think of 3 and 4; I think it's plausible you're right (and either way I suspect I'll learn something useful from thinking it through).
In the first model I thought through, though, I don't think that you're right: if you train a model with RL with a KL penalty, it will end up with a policy that outputs a distribution over answers which is equivalent to taking the generative distribution and then applying a Boltzmann factor to upweight answers that your overseer likes. AFAICT this doesn't generally induce more causal Goodhart problems than best-of-N selection does.
(I might be wrong though, I'd appreciate a second opinion.)
I don't feel totally satisfied by this argument though, because RL with KL penalty generally seems kind of unprincipled to me. I'd rather have an argument that didn't rely on the KL penalty. I am unsure whether other reasonable models of RL will similarly not have the causal Goodhart problem. I'll keep thinking about it for a bit and would be interested in someone else working it out.
(The worked example in this comment was a joint effort with Eric Neyman and Drake Thomas.)
Here's a toy example in which we get worse Goodharting for RL than for filtering: suppose that our model has three submodules
- A, which tries to produce outputs which are both true and persuasive
- B, which tries to produce outputs which are true, but have no effect on persuasiveness
- C, which tries to produce outputs which are persuasive, but with no effect on truthiness.
Our model has parameters summing to 1 which determine how much to listen to each of these submodules. More specifically, our submodules produce samples from the normal distributions , respectively, and then our model puts these samples together to produce an output which has truth score
and persuasiveness score
.
We'll assume that we're only able to measure persuasiveness, but that we want truthiness.(Some unstated assumptions: with and .)
Our model was trained on data in which truthiness and persuasiveness were positively correlated; this will be reflected in having , so that and are positively correlated. If this is true, then conditioning on some persuasiveness score results in getting an output with expected truthiness score
.
Note that this scales linearly with , so that as we ask for more persuasiveness, we get more truthiness on average, as we'd hope.
In contrast, suppose we do RL on our model for high persuasiveness scores; imagine that this doesn't change the submodules A, B, and C much, but does tune the parameters . Then:
- if we'll set , i.e. always use the submodule which tries to produce true and persuasive outputs. This will result in average truthiness .
- but if we'll set , i.e. always use the submodule which tries to be persuasive but not true. This will result in average truthiness , much worse than we would get if we had done filtering.
Really this is just a dressed-up version of the classic Goodharting story, where you have a constrained resource () to allocate among various options(=the submodules A,B,C), so you put 100% of your resources into the option which is cheapest in persuasiveness-per-resource; unfortunately, this was not the option which gave the best truth-per-resource.
Some misc comments:
- This example was a bit silly, but I think it captures some pieces of many folks' intuitions around RL and Goodharting: pretrained models have lots of capabilities, which are in some sense competing for the steering wheel: you can't LARP an economist writing an excellent paper and simultaneously LARP a deceptive agent who wants paperclips but finds it instrumentally useful to write economics papers. Whichever capability scores best for your proxy will win out, and with all other possible ways the model could have completed the training task getting no say.
- By thinking of "persuasiveness" as being something which we actually wanted to get, this example also serves as an illustration of how filtering can be uncompetitive: filtering produces outputs whose persuasiveness is distributed as whereas RL produces a model whose outputs have persuasiveness on average; if is large, that means that you'd have to filter roughly the order of outputs to get the same persuasiveness as the average output of the RL-optimized model.
- I spent a while confused about how this squares with the baseline-probability-time-Boltzman-factor classification of what RL with a KL penalty will converge to. (The example above didn't have a KL penalty, but adding a small one wouldn't have much much difference.) I think the answer is that the model I described wasn't expressive enough to represent the baseline-probability-time-Boltzman-factor distribution that RL with a KL penalty would optimally converge to. This lack of expressivity seems quite related to the fact our model was a linear combination of three distributions which we modeled as not changing throughout training. That means that this story, which is based on the frame that generative models are a giant pile of capabilities which can be elicited, is in tension with the frame that neural networks are flexible function approximators; I found this pretty interesting.
- All this being said, I'm pretty skeptical that whatever sort of Goodharting is being captured in this example has much to do with the sort of Goodharting we empirically observe in RLHF, since this example doesn't work with best-of-n optimization (whereas extremal Goodharting does occur for best-of-n, as Buck pointed out elsethread).
- Overall, I don't put much stock in this example beyond helping articulate the point that RL amplifies capabilities in proportion to how causally downstream of high-reward outputs they are, whereas filtering only takes into account their correlations with high-reward outputs.
Note that in this example your model is unable to sample from the conditional you specified, since it is restricted to . In this regime truthfulness and persuasiveness are anticorrelated because of a capability constraint of your model, it just literally isn't able to increase both at the same time, and conditioning can do better because you are generating lots of samples and picking the best.
(You point this out in your comment, but it seems worth emphasizing. As you say, if you do RL with a KL penalty, then the capability limit is the only way you can get this kind of mismatch. Without a KL penalty the exact behavior of RL vs conditioning will depend on details of gradient descent, though it seems quite similar in practice and I'm not sure which way this comparison goes.)
In terms of being able to sample from the conditional, I don't think that the important constraint here is . Rather, it seems that the important constraint is that our architecture can only sample from distributions of the form ; even allowing to be arbitrary real numbers, this will never be the same as either (a) the distribution produced by conditioning the base model on high persuasiveness, or (b) the distribution which maximizes expected persuasiveness - KL divergence from the base model.
I'm not sure the above point as an important one. I just wanted to disambiguate some different capabilities limitations which appeared in the example:
- limitations on what sorts of distributions the architecture could approximate
- limitations on the latent capabilities in the base model for producing true/persuasive outputs
- limitations on how much steering each of the various latent capabilities gets to exert ().
On my understanding, your point was about limitation (1). But I don't feel especially nervous about limitation (1) -- taking the output distribution of our pretrained model and weighting it by a Boltzman factor feels like it should produce a kinda crazy distribution, and my naive intuition is that we shouldn't necessarily expect our model to be able to approximate this distribution that well after RL finetuning with a KL penalty.
I think I'm most nervous about the way we modeled limitation (3): I have no idea how to think about the extent to which models' capabilities trade off against one another, and taking without additional constraints would have resulted in outputs of mean truthiness for some which we can't pin down without specifying additional details (e.g. is there weight decay?).
I'm also most nervous about this way of modeling limitation (2)/(3), since it seems like it leads directly to the conclusion "fine-tuning always trades off truthfulness and persuasion, but conditioning can improve both."
Boltzmann factor to upweight answers that your overseer likes. AFAICT this doesn't generally induce more causal Goodhart problems than best-of-N selection does.
This seems correct insofar as your proxy reward does not have huge upward errors (that you don't remove via some sort of clipping). For example, if there's 1 million normal sentences with reward uniformly distributed between [0, 100] and one adversarial sentence with reward r=10^5, conditioning on reward>99 leads to a 1/10,000 chance of sampling the adversarial sentence, while it's very tricky (if not impossible) to correctly set the KL penalty so you end up optimizing reward without just outputting the adversarial sentence over and over again.
I don't feel totally satisfied by this argument though, because RL with KL penalty generally seems kind of unprincipled to me. I'd
I don't think it's particularly unprincipled; the KL penalty is just our way of encoding that the base policy is relatively reasonable (in a value-free way), and the model shouldn't deviate from it too much. Similarly, BoN is another way of encoding that the base policy is reasonable, albeit one that's easier to reason about on average.
Another way people regularize their RL is to mix in self-supervised training with RL (for example, they did this for text-davinci-003). I'm pretty sure this is also equivalent to RL w/ KL penalty.
I am unsure whether other reasonable models of RL will similarly not have the causal Goodhart problem.
There's the impact penalties approach (e.g. AUP or RLSP), which seem more principled than KL penalties in cases where you more information on the space of rewards.
You can also write do constrained optimization, which is again equivalent to modifying the reward function, but is way easier for humans to reason about and give feedback on.
In the first model I thought through, though, I don't think that you're right: if you train a model with RL with a KL penalty, it will end up with a policy that outputs a distribution over answers which is equivalent to taking the generative distribution and then applying a Boltzmann factor to upweight answers that your overseer likes. AFAICT this doesn't generally induce more causal Goodhart problems than best-of-N selection does.
As far as I can tell, the argument for this assumes that the model can generalise the reward function perfectly, which seems questionable because it only sees a few samples of the reward function (call this claim 1).
One possibility is that the Boltzmann factor upweights answers the model is confident the overseer will like more than answers it's less confident about. This could end up applying pressure to concentrate on high-confidence approved answers, which could break desirable correlations (call this claim 2).
I'm fairly confident in the claim that in general a Bayesian learner will not generalise the reward function perfectly (claim 1); how the reward function generalises will typically depend on the posterior over parameters and there are different posteriors that yield the same distribution over texts (Sam's sibling comment illustrates this point). I've no idea about what's going on with transformers, though - they can generalise text prediction quite well, so maybe they generalise approval quite well too, but that's just a wild guess. Claim 2 is idle speculation that I only mean to illustrate the point about pressure to break desirable correlations.
This is very interesting. I had previously thought the “KL penalty” being used in RLHF was just the local one that’s part of the PPO RL algorithm, but apparently I didn’t read the InstructGPT paper carefully enough.
I feel slightly better about RLHF now, but not much.
It’s true that minimizing KL subject to a constraint of always exceeding a certain reward threshold would theoretically be equivalent to Bayesian conditioning and therefore equivalent to filtering. That could be seen as a lexicographic objective where the binarised reward gets optimised first and then the KL penalty relative to the predictive model would restore the predictive model’s correlations (once the binarised reward is absolutely saturated). Unfortunately, this would be computationally difficult with gradient descent since you would already have mode-collapse before the KL penalty started to act.
In practice (in the InstructGPT paper, at least), we have a linear mixture of the reward and the global KL penalty. Obviously, if the global KL penalty is weighted at zero, it doesn’t help avoid Causal Goodhart, nor if it’s weighted at . Conversely, if it’s weighted at , the model won’t noticeably respond to human feedback. I think this setup has a linear tradeoff between how much helpfulness you get and how much you avoid Causal Goodhart.
The ELBO argument in the post you linked requires explicitly transforming the reward into a Boltzmann distribution (relative to the prior of the purely predictive model) before using it in the objective function, which seems computationally difficult. That post also suggests some other alternatives to RLHF that are more like cleverly accelerated filtering, such as PPLM, and has a broad conclusion that RL doesn’t seem like the best framework for aligning LMs.
That being said, both of the things I said seem computationally difficult above also seem not-necessarily-impossible and would be research directions I would want to allocate a lot of thought to if I were leaning into RLHF as an alignment strategy.
It’s true that minimizing KL subject to a constraint of always exceeding a certain reward threshold would theoretically be equivalent to Bayesian conditioning and therefore equivalent to filtering.
It's also true that maximizing Reward - KL is Bayesian updating as the linked post shows, and it's true that maximizing reward subject to a KL constraint is also equivalent to Bayesian updating as well (by Lagrangian multipliers). You see similar results with Max Ent RL (where you maximize Reward + Entropy, which is equal to a constant minus the KL relative to a uniform distribution), for example.
Unfortunately, this would be computationally difficult with gradient descent since you would already have mode-collapse before the KL penalty started to act.
Sounds like you need to increase the KL penalty, then!
I think this setup has a linear tradeoff between how much helpfulness you get and how much you avoid Causal Goodhart.
I don't see why this argument doesn't also apply to the conditioning case -- if you condition on a proxy reward being sufficiently high, you run into the exact same issues as w/ KL regularized RL with binarized reward.
requires explicitly transforming the reward into a Boltzmann distribution
This seems like a misunderstanding of the post (and the result in general) -- it shows that doing RL with KL constraints is equivalent to Bayesian updating the LM prior with a likelihood (and the update people use in practice is equivalent to variational inference). You wouldn't do this updating explicitly, because computing the normalizing factor is too hard (as usual); instead you just optimize RL - KL as you usually would.
(Or use a decoding scheme to skip the training entirely; I'm pretty sure you can just do normal MCMC or approximate it with weight decoding/PPLM.)
Firstly, a clarification: I don't want to claim that RL-with-KL-penalty policies are the same as the results of conditioning. I want to claim that you need further assumptions about the joint distribution of (overseer score, true utility) in order to know which produces worse Goodhart problems at a particular reward level (and so there's no particular reason to think of RL as worse).
It’s true that minimizing KL subject to a constraint of always exceeding a certain reward threshold would theoretically be equivalent to Bayesian conditioning and therefore equivalent to filtering. [...]In practice (in the InstructGPT paper, at least), we have a linear mixture of the reward and the global KL penalty. [...]
I thought that using linear mixture of reward and global KL penalty is (because of a Lagrange multiplier argument) the same as having a constraint on reward while minimizing KL penalty?
Maybe the point you're making is that the KL between the policy and the original generative model is different on different inputs? I agree that this means that the RL policy is different than the best-of-n policy, but I don't see why either has predictably worse Goodhart problems.
It's not clear to me that 3. and 4. can both be true assuming we want the same level of output quality as measured by our proxy in both cases. Sufficiently strong filtering can also destroy correlations via Extremal Goodhart (e.g. this toy example). So I'm wondering whether the perception of filtering being safer just comes from the fact that people basically never filter strongly enough to get a model that raters would be as happy with as a fine-tuned one (I think such strong filtering is probably just computationally intractable?)
Maybe there is some more detailed version of your argument that addresses this, if so I'd be interested to see it. It might argue that with filtering, we need to apply less selection pressure to get the same level of usefulness (though I don't see why), or maybe that Goodhart's law kicks in less with filtering than with RLHF for some reason.
Extremal Goodhart relies on a feasibility boundary in -space that lacks orthogonality, in such a way that maximal logically implies non-maximal . In the case of useful and human-approved answers, I expect that in fact, there exist maximally human-approved answers that are also maximally useful—even though there are also maximally human-approved answers that are minimally useful! I think the feasible zone here looks pretty orthogonal, pretty close to a Cartesian product, so Extremal Goodhart won't come up in either near-term or long-term applications. Near-term, it's Causal Goodhart and Regressional Goodhart, and long-term, it might be Adversarial Goodhart.
Extremal Goodhart might come into play if, for example, there are some truths about what's useful that humans simply cannot be convinced of. In that case, I am fine with answers that pretend those things aren't true, because I think the scope of that extremal tradeoff phenomenon will be small enough to cope with for the purpose of ending the acute risk period. (I would not trust it in the setting of "ambitious value learning that we defer the whole lightcone to.")
For the record, I'm not very optimistic about filtering as an alignment scheme either, but in the setting of "let's have some near-term assistance with alignment research", I think Causal Goodhart is a huge problem for RLHF that is not a problem for equally powerful filtering. Regressional Goodhart will be a problem in any case, but it might be manageable given a training distribution of human origin.
Idk, if you're carving up the space into mutually exclusive "Causal Goodhart" and "Extremal Goodhart" problems, then I expect conditioning to have stronger Extremal Goodhart problems, just because RL can change causal mechanisms to lead to high performance, whereas conditioning has to get high performance just by sampling more and more extreme outputs.
(But mostly I think you don't want to carve up the space into mutually exclusive "Causal Goodhart" and "Extremal Goodhart".)
Extremal Goodhart is different from other forms of Goodhart in that a maximal value of something will always lead to less or zero true reward.
This is difficult to show, since you need to show that anything you maximize implies non maximal true reward. And that's different from causal Goodhart, where the causal relationship is mistaken.
Thanks! Causal Goodhart is a good point, and I buy now that RLHF seems even worse from a Goodhart perspective than filtering. Just unsure by how much, and how bad filtering itself is. In particular:
In the case of useful and human-approved answers, I expect that in fact, there exist maximally human-approved answers that are also maximally useful
This is the part I'm still not sure about. For example, maybe the simplest/apparently-easiest-to-understand answer that looks good to humans tends to be false. Then if human raters prefer simpler answers (because they're more confident in their evaluations of those), the maximally approved answers might be bad. This is similar to the truths humans can't be convinced of you mention, but with the difference that it's just a matter of how convinced humans are by different answers. We could then be in a situation where both filtering and RLHF suffer a lot from Goodhart's law, and while RLHF might technically be even worse, the difference wouldn't matter in practice since we'd need a solution to the fundamental problem anyway.
I feel like the key question here is how much selection pressure we apply. My sense is that for sufficient amounts of selection pressure, we do quite plausibly run into extremal Goodhart problems like that. But it also seems plausible we wouldn't need to select that hard (e.g. we don't need the single most compelling answer), in which case I agree with what you said.
As a caveat, I didn't think of the RL + KL = Bayesian inference result when writing this, I'm much less sure now (and more confused).
Anyway, what I meant: think of the computational graph of the model as a causal graph, then changing the weights via RLHF is an intervention on this graph. It seems plausible there are somewhat separate computational mechanisms for producing truth and for producing high ratings inside the model, and RLHF could then reinforce the high rating mechanism without correspondingly reinforcing the truth mechanism, breaking the correlation. I certainly don't think there will literally be cleanly separable circuits for truth and high rating, but I think the general idea plausibly applies. I don't see how anything comparable happens with filtering.
I think your claim is something like:
Without some form of regularization, some forms of RL can lead to trajectories that have zero probability wrt the base distribution (e.g. because they break a correlation that occurs on the pretraining distribution with 100% accuracy). However, sampling cannot lead to trajectories with zero probability?
As stated, this claim is false for LMs without top-p sampling or floating point rounding errors, since every token has a logit greater than negative infinity and thus a probability greater than actual 0. So with enough sampling, you'll find the RL trajectories.
This is obviously a super pedantic point: RL finds sentences with cross entropy of 30+ nats wrt to the base distribution all the time, while you'll never do Best-of-exp(30)~=1e13. And there's an empirical question of how much performance you get versus how far your new policy is from the old one, e.g. if you look at Leo Gao's recent RLHF paper, you'll see that RL is more off distribution than BoN at equal proxy rewards.
That being said, I do think you need to make more points than just "RL can result in incredibly implausible trajectories" in order to claim that BoN is safer than RL, since I claim that Best-of-exp(30) is not clearly safe either!
No, I'm not claiming that. What I am claiming is something more like: there are plausible ways in which applying 30 nats of optimization via RLHF leads to worse results than best-of-exp(30) sampling, because RLHF might find a different solution that scores that highly on reward.
Toy example: say we have two jointly Gaussian random variables X and Y that are positively correlated (but not perfectly). I could sample 1000 pairs and pick the one with the highest X-value. This would very likely also give me an unusually high Y-value (how high depends on the correlation). Or I could change the parameters of the distribution such that a single sample will typically have an X-value as high as the 99.9th percentile of the old distribution. In that case, the Y-value I typically get will depend a lot on how I changed the parameters. E.g. if I just shifted the X-component of the mean and nothing else, I won't get higher Y-values at all.
I'm pretty unsure what kinds of parameter changes RLHF actually induces, I'm just saying that parameter updates can destroy correlations in a way that conditioning doesn't. This is with the same amount of selection pressure on the proxy in both cases.
RLHF could then reinforce the high rating mechanism without correspondingly reinforcing the truth mechanism, breaking the correlation.
I unconfidently think that in this case, RLHF will reinforce both mechanisms, but reinforce the high rating mechanism slightly more, which nets out to no clear difference from conditioning. But I wouldn't be shocked to learn I was wrong.
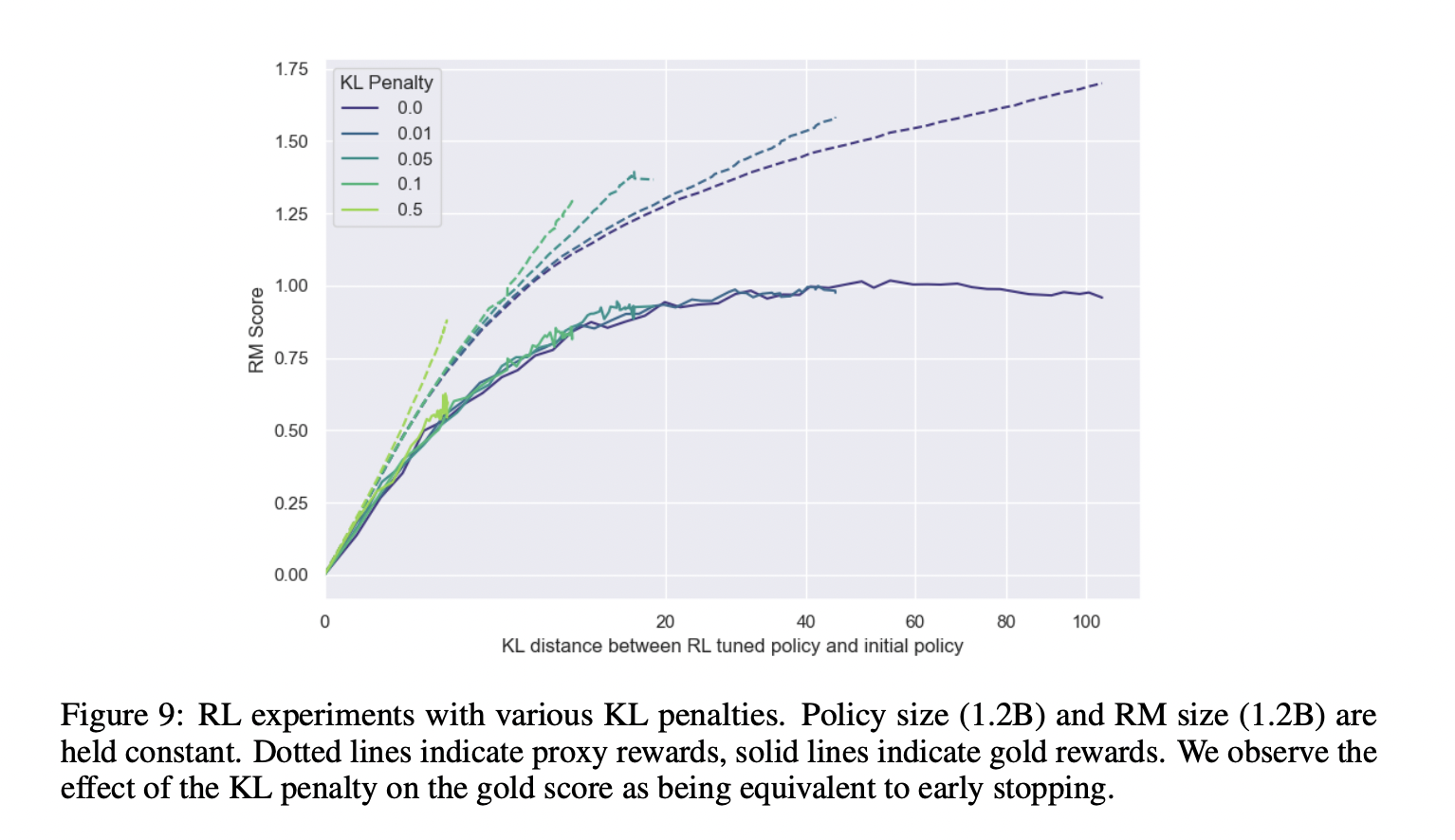
Incidentally, I doubt either of us considers this kind of empirical evidence much of an update about the long-term situation, but Gao et al compare best-of-N and RL and find that "the relationship between the proxy reward model score and the gold reward model score is similar for both methods." (Thanks to Ansh Radhakrishnan for pointing this out.)
I agree with the general point, but I'll note that at equal proxy reward model scores, the RL policy has significantly more KL divergence with the base policy.
That’s not the case when using a global KL penalty—as (I believe) OpenAI does in practice, and as Buck appeals to in this other comment. In the paper linked here a global KL penalty is only applied in section 3.6, because they observe a strictly larger gap between proxy and gold reward when doing so.
This doesn't seem to be what Gao et al found: Figure 9 shows that the KL between RL and initial policy, at a given proxy reward score, still is significantly larger than the equivalent KL for a BoN-policy, as shown in Figure 1.
In RLHF there are at least three different (stochastic) reward functions:
- the learned value network
- the “human clicks 👍/👎” process, and
- the “what if we asked a whole human research group and they had unlimited time and assistance to deliberate about this one answer” process.
I think the first two correspond to what that paper calls “proxy” and “gold” but I am instead concerned with the ways in which 2 is a proxy for 3.
I’m not really aware of any compelling alternatives to this class of plan–“training a model based on a reward signal” is basically all of machine learning
I think the actual concern there is about human feedback, but you phrased the question as about overseer feedback, but then your answer (quoted) is about any reward signal at all.
Is next-token prediction already “training a model based on a reward signal”? A little bit—there’s a loss function! But is it effectively RL on next-token-prediction reward/feedback? Not really. Next-token prediction, by contrast to RL, only does one-step lookahead and doesn’t use a value network (only a policy network). Next-token prediction is qualitatively different from RL because it doesn’t do any backprop-through-time (which can induce emergent/convergent forward-looking “grooves” in trajectory-space which were not found in the [pre]training distribution).
Perhaps more importantly, maintaining some qualitative distance between the optimisation target for an AI model and the human “does this look good?” function seems valuable, for similar reasons to why one holds out some of the historical data while training a financial model, or why one separates a test distribution from a validation distribution. When we give the optimisation process unfettered access to the function that’s ultimately going to make decisions about how all-things-considered good the result is, the opportunities for unmitigated overfitting/Goodharting are greatly increased.
I still don't think you've proposed an alternative to "training a model with human feedback". "maintaining some qualitative distance between the optimisation target for an AI model and the human “does this look good?” function" sounds nice, but how do we even do that? What else should we optimise the model for, or how should we make it aligned? If you think the solution is use AI-assisted humans as overseers, then that doesn't seem to be a real difference with what Buck is saying. So even if he actually had written that he's not aware of an alternative to "training a model with human/overseer feedback", I don't think you've refuted that point.
(A few of the words in this post were written by Ryan Greenblatt and Ajeya Cotra. Thanks to Oliver Habryka and Max Nadeau for particularly helpful comments.)
Sometimes people want to talk about whether RLHF is “a promising alignment strategy”, or whether it “won’t work” or “is just capabilities research”. I think that conversations on these topics are pretty muddled and equivocate between a bunch of different questions. In this doc, I’ll attempt to distinguish some of these questions, and as a bonus, I’ll give my opinions on them.
I wrote this post kind of quickly, and I didn’t have time to justify all the claims I make; I hope that this post is net helpful anyway. I’m sympathetic to claims that alignment researchers should err more on the side of writing fewer but better posts; maybe I’ll regret making this one now instead of waiting.
That said, I’m less convinced than the median LessWrong commenter that speeding up AGI is bad right now, mostly because I partially agree with the argument in the first bullet point here.