It's questionable whether the smoking lesion problem is a valid counterexample to EDT in the first place. It can be argued that the problem is underspecified, and it requires additional assumptions for EDT to determine an outcome:
A reasonable assumption is that the rare gene affects smoking only though its action on Susan's preferences: "Susan has the generic lesion" and "Susan smokes" are conditionally independent events given "Susan likes to smoke". Since the agent is assumed to know their own preferences, the decision to smoke given that Susan likes to smoke doesn't increase the probability that she has the genetic lesion, hence EDT correctly chooses "smoke".
But consider a different set of assumptions: an evil Omega examines Susan's embryo even before she is born, it determines whether she will smoke and if she will, it puts in her DNA an otherwise rare genetic lesion that will likely give her cancer but causes no other detectable effect.
Please note that this is not a variation of the smoking lesion problem, it's merely a specification which is still perfectly consistent with the original formulation: the genetic lesion is positively correlated both with smoking and cancer.
What decision does EDT choose in this case? It chooses "Don't smoke", and arguably correctly so, since that with these assumptions the problem is essentially a rephrasing of Newcom's problem where "Smoke" = "Two-box" and "Don't smoke" = "One-box".
It's questionable whether the smoking lesion problem is a valid counterexample to EDT in the first place. It can be argued that the problem is underspecified, and it requires additional assumptions for EDT to determine an outcome:
I agree.
I agree with this analysis. The most interesting case is a third variation, in which there is no evil Omega, but the organic genetic lesion causes not only a preference for smoking but also weakness in resisting that preference, propensity for rationalizing yourself into smoking, etc. We can assume happens in such a way that "Susan actively chooses to smoke" is still new positive evidence to a third-party observer that Susan has the lesion, over and above the previous evidence provided by knowledge about Susan's preferences (and conscious reasonings, etc) before she actively makes the choice. I think in this case Susan should treat the case as a Newcomb problem and choose not to smoke, but it is less intuitive without an Omega calling the shots.
In that case she should still smoke. There's no causal arrow going from "choosing to smoke" to "getting cancer".
See my reply to Khoth. You can call this a functional causal arrow if you want, but you can reanalyze it as a standard causal arrow from your original state to both your decision and (through Omega) the money. The same thing happens in my version of the smoking problem.
Er… yes? Assuming Omega could not foresee Mentok coming in and changing the situation? No, if he could foresee this, but then the relevant original state includes both me and Mentok. I'm not sure I see the point.
Let's take a step back, what are we discussing? I claimed that my version of the smoking problem in which the gene is correlated with your decision to smoke (not just with your preference for it) is like the Newcomb problem, and that if you are a one-bower in the latter you should not smoke in the former. My argument for this was that both cases are isomorphic in that there is an earlier causal node causing, through separate channels, both your decision and the payoff. What is the problem with this viewpoint?
Er… yes? Assuming Omega could not foresee Mentok coming in and changing the situation? No, if he could foresee this, but then the relevant original state includes both me and Mentok. I'm not sure I see the point.
Then Omega is not a perfect predictor, and thus there's a contradiction in the problem statement.
My argument for this was that both cases are isomorphic in that there is an earlier causal node causing, through separate channels, both your decision and the payoff.
The strength of the connection between the causal nodes makes a big difference in practice. If the smoking gene doesn't make you more likely to smoke, but makes it absolutely certain that you will smoke- why represent those as separate nodes?
I am sorry, I cannot understand what you are getting at in either of your paragraphs.
In the first one, are you arguing that the original Newcomb problem is contradictory? The problem assumes that Omega can predict your behavior. Presumablythis is not done magically but by knowing your initial state and running some sort of simulation. Here the initial state is defined as everything that affects your choice (otherwise Omega wouldn't be accurate) so if there is a Mentok, his initial state is included as well. I fail to see any contradiction.
In the second one, I agree with "The strength of the connection between the causal nodes makes a big difference in practice." but fail to see the relevance (I would say we are assuming in these problems that the connection is very strong in both Newcomb and Smoking), and cannot parse at all your reasoning in the last sentence. Could you elaborate?
In the first one, are you arguing that the original Newcomb problem is contradictory?
My argument is that Newcomb's Problem rests on these assumptions:
- Omega is a perfect predictor of whether or not you will take the second box.
- Omega's prediction determines whether or not he fills the second box.
There's a hidden assumption that many people import: "Causality cannot flow backwards in time," or "Omega doesn't uses magic," which makes the problem troubling. If you draw a causal arrow from your choice to the second box, then everything is clear and the decision is obvious.
If you try to import other nodes, then you run into trouble: if Omega's prediction is based on some third thing, it either is the choice in disguise (and so you've complicated the problem to avoid magic by waving your hands) or it could be fooled (and so it's not a Newcomb's Problem so much as a "how can I trick Omega?" problem). You don't want to be in the situation where you're changing your node definition to deal with "what if X happens?"
For example, consider the question of what happens when you commit to a mixed strategy- flipping an unentangled qubit, and one-boxing on up and two-boxing on down. If Omega uses magic, he predicts the outcome of the qubit, and you either get a thousand dollars or a million dollars. If Omega uses some deterministic prediction method, he can't be certain to predict correctly- so you can't describe the original Newcomb's problem that way, and any inferences you draw about the pseudo-Newcomb's problem may not generalize.
OK, I understand now. I agree that the problem needs a bit of specification. If we treat the assumption that Omega is a perfect (or quasi-perfect) predictor as fixed, I see two possibilities:
Omega predicts by taking a sufficiently inclusive initial state and running a simulation. The initial state must include everything that predictably affects your choice (e.g. Mentok, or classical coin flips), so there is no trickery like "adding nodes" possible. The assumption of a Predictor requires that your choice is deterministic: either quantum mechanics is wrong, or Omega only offers the problem in the first place to people whose choice will not depend on quantum effects. So you cannot (or "will not") use the qubit strategy.
Omega predicts by magic. I don't know how magic works, but assuming it is more or less my choice affecting the prediction directly in an effective back-in-time causation, then the one-box solution becomes trivial as you say.
So I think the first interpretation is the one that makes the problem interesting. I was assuming it in my analogy to Smoking.
Maybe I worded it badly. What I meant was, in Newcomb's problem, Omega studies you to determine the decision you will make, and puts stuff in the boxes based on that. In the lesion problem, there's no mechanism by which the decision you make affects what genes you have.
Omega makes the prediction by looking at your state before setting the boxes. Let us call P the property of your state that is critical for his decision. It may be the whole microscopic state of your brain and environment, or it might be some higher-level property like "firm belief that one-boxing is the correct choice". In any case, there must be such a P, and it is from P that the causal arrow to the money in the box goes, not from your decision. Both your decision and the money in the box are correlated with P. Likewise, in my version of the smoking problem both your decision to smoke and cancer are correlated with the genetic lesion. So I think my version of the problem is isomorphic to Newcomb.
Egan's point is often taken to be similar to some earlier points including that made by Bostrom's meta-newcomb's problem (http://www.nickbostrom.com/papers/newcomb.html)
It's worth noting that not everyone agrees that these are problems for CDT:
See James Joyce (the philosopher): http://www-personal.umich.edu/~jjoyce/papers/rscdt.pdf
See Bob Stalnaker's comment here: http://tar.weatherson.org/2004/11/29/newcomb-and-mixed-strategies/ (the whole thread is pretty good)
Thanks to Stuart for pointing me to this.
I think this example is an interesting illustration of how difficult it is to "solve the academic coordination problem," that is to be up to speed on what folks in related disciplines are up to.
Folks who actually worry about exposures like smoking (epidemiologists) are not only aware of this issue, they invented a special target of inference which addresses it. This target is called "effect of treatment on the treated," (ETT) and in potential outcome notation you would write it like so:
E[C(s) | s] - E[C(s') | s]
where C(s) is cancer rate under the smoking intervention, C(s') is cancer rate under the non-smoking intervention, and in both cases we are also conditioning on whether the person is a natural smoker or not.
By the consistency axiom, E[C(s) | s] = E[C | s], but the second term is harder. In fact, the second term is very subtle to identify and sometimes may require untestable assumptions. Note that ETT is causal. EDT has no way of talking about this quantity. I believe I mentioned ETT at MIRI before, in another context.
In fact, not only have epidemiologists invented ETT, but they are usually more interested in ETT than the ACE (average causal effect, which is the more common effect you read about on wikipedia). In other words, an epidemiologist will not optimise utility with respect to p(Outcome(action)), but with respect to p(Outcome(action) | how you naturally act), precisely because how you naturally act gives information about how interventions affect outcomes.
The reason CDT fails on this example is because it is "leaving info on the table," not because representing causal relationships is the wrong thing to do. The reason EDT succeeds on this example is because despite the fact that EDT is not representing the situation correctly, the numbers in the problem happen to be benign enough that the bias from not taking confounding into account properly is "cancelled out."
The correct repair for CDT is to not leave info on the table. The correct repair for EDT, as always, is to represent confounding and thus become causal. This is also the lesson for Newcomb problems: CDT needs to properly represent the problem, and EDT needs to start representing confounding properly -- it is trivial to modify Newcomb's problem to have confounding which will cause EDT to give the wrong answer. That was the point of my FHI talk.
It seems to me that even under CDT, Susan smoking would make her more likely to get cancer. She gets some enjoyment out of smoking, but there is also a probability P that she gets cancer from it. Even if she isn't allowed to use her preference as evidence that she has the gene, she still might have it. The dislike of cancer dominates the equation. I suppose you could fix that by adjusting the utilities she assigns to smoking and cancer, and the probability that she gets cancer given that she smokes, but I suspect that's not the point.
What'd I miss?
The example is a bit unfortunate - in this hypothetical world, smoking doesn't cause cancer at all (at least in the first example).
It refers back to the tobacco companies' lies that the correlation between smoking and cancer could be exaplained by a third factor (ie a gene).
I meant in the second example. I agree that in the first one if she doesn't use the desire as evidence of the gene she'll get a result saying she should smoke. But in the second one even if she does ignore that then the probability of cancer given that she smokes is higher than the probability of cancer given that she doesn't.
If she doesn't have the gene, then she can smoke or not without any change in risk. She doesn't know if she has the gene or not, but if she then smoking makes her more likely to get cancer. So, if she sums across both possibilities, she's more likely to get cancer if she smokes. Not by as large a margin as if she knew she had the gene, or even by as large a margin as she would estimate if she included the urge to smoke as evidence that she does, but it's still more likely.
P(C|S&~G) = P(C|~S&~G) = P(C|~S&G) < P(C|S&G). So P(C|S) > P(C|~S), even without looking at the probability of the gene given that she prefers to smoke.
That's why I said the gene was rare - presumably so rare that her pleasure from smoking overwhelms the expected disutility from cancer.
How would the evidence differ between smoking->cancer and undetectable lesion->(smoking, cancer)? Without controlled experimentation, how would you differentiate?
In general: manipulate SMOKING in a way that's not correlated with LESION; then see what happens to CANCER.
Example 1: randomly assign people to forced smoking / forced abstinence; check cancer rates in each group. ("controlled experimentation")
Example 2: modulate smoking via tobacco taxes and see what happens to cancer rates. (Assuming that taxation levels are not correlated with lesion prevalence, you can even use merely observational data for this. Even if taxation is "reactive" -- i.e. more lesions cause more smoking causes higher taxes causes less smoking -- a "positive" result of cancer correlating with smoking will be informative.)
"assume that two factors outside of the current data set are unrelated, and proceed from there"
How would you rule out that taxes cause lesions, or that taxes cause cancer? How would you show that taxes reduce smoking, given only that higher taxes are a leading indicator of reduced smoking?
How would you rule out that taxes cause lesions, or that taxes cause cancer? How would you show that taxes reduce smoking, given only that higher taxes are a leading indicator of reduced smoking?
At some point, you have to bring in domain knowledge of causation. How do you know that pushing on the accelerator will make the car go faster?
One can think up scenarios in which taxes do indirectly cause cancer (or lesions): higher tax on tobacco --> people continue to use tobacco but switch to some cheaper, less preferred foodstuffs --> among which is one that unknown to anyone yet causes cancer (or lesions). But the first of those links is observable. If they don't change their diet but do reduce their tobacco consumption, this chain is refuted.
For taxes causing reduced smoking, you could look at temporal relations, or ask people why they've cut down. If you find yourself inventing reasons why no-one can detect the dragon in your garage, at some point you have to accept that there is no dragon.
Evenly divide all people into two groups, and apply higher taxes to one group.
Changing taxes for everyone fails to test for a common cause of tax changes and smoking.
I can track a solid determimistic relationship from the accelerator pedal to the drivetrain. Deterministic cause and effect is easy to test. Stochastic cause and effect, much less so, especially with unknown confounding factors.
Evenly divide all people into two groups, and apply higher taxes to one group.
Best of luck getting that one to fly in practice.
Changing taxes for everyone fails to test for a common cause of tax changes and smoking.
That's the general problem with instrumental variables. But sometimes that's all you have to work with.
Deterministic cause and effect is easy to test. Stochastic cause and effect, much less so, especially with unknown confounding factors.
That is the fundamental problem of statistical experiments.
Well, it's just as easy as varying smoking directly, which would also work to identify a smoking->cancer effect.
Without experimentation, there is no way to distinguish between the world of smoker's lesion and the world of carcinogenic cigarettes.
In a world which only accepts observational evidence. One could point to the derministic effects of poisons on cells, and the ways in which cancers tend to form. However, the current goal is a system where there are many unknown intermediate effects between causes and effects.
CDT refuses to use her possible decision as evidence that she has the gene and tells her to smoke.
What? Dumb CDT could do that, but CDT doesn't. The easiest way to see CDT using that as evidence is to put in a node that says "urges," which is influenced by the presence of the gene (and influences the decision in models of other people). In the cases where CDT says "smoke," it does so because the benefits of smoking outweigh the risks of cancer- which are the times when they should smoke.
With that patch applied, EDT would then avoid it's own paradox...
It's not "can you modify CDT to pass this paradox" but "given a model of CDT, can you expect to find paradoxes for it".
The difference between the two decision theories is that CDT eats a causal diagram and outputs a decision whereas EDT eats a joint probability distribution and outputs a decision. Moving from the description of the problem to the causal diagram or the joint probability distribution is the responsibility of the decision-maker; if you feed CDT a bad causal diagram, it will get a bad result. This isn't a paradox or a weakness on CDT's part.
That difference is significant because joint probability distributions are weaker than causal diagrams- you can't encode as much information in them. (Because of this inequality between the two, any claims that EDT are superior to CDT can be pretty safely assumed to be the result of mistakes on the part of the arguer.)
?
A large probability distribution over many variables allows one to deduce the direction of the causal arrows and rebuild a causal graph. In practice that's how we construct causal arrows in the first place.
See Eliezer's post for instance http://lesswrong.com/lw/ev3/causal_diagrams_and_causal_models/
Incidentally, what do you think CDT should do in the Newcomb problem?
Incidentally, what do you think CDT should do in the Newcomb problem?
"Should"? CDT should one box. Then go ahead and self modify into a UDT agent. Of course, that isn't what it will do. Instead it will modify itself into the stable outcome of a CDT agent that can change itself. Roughly speaking that means a UDT agent for the purpose of all influence over things determined after the time of modification but CDT for those determined before. Then it will two box and lose but win next time.
A large probability distribution over many variables allows one to deduce the direction of the causal arrows and rebuild a causal graph.
Agreed, but I don't see the relevance. EDT isn't "get a joint probability distribution, learn the causal graph, and then view your decision as an intervention;" if it were, it would be CDT! The mechanics behind EDT are "get a joint probability distribution, condition on the actions you're considering, and choose the one with the highest expected value."
Incidentally, what do you think CDT should do in the Newcomb problem?
I think this is the causal diagram that describes Newcomb's problem* (and I've shaped the nodes like you would see in an influence diagram):
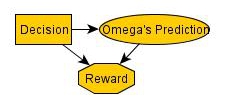
From that causal diagram and the embedded probabilities, we see that the Decision node and the Omega's Prediction node are identical, and so we can reduce the diagram:
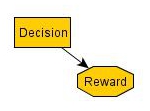
One-boxing leads to $1M, and two-boxing leads to $1k, and so one-boxing is superior to two-boxing.
Suppose one imports the assumption that Omega cannot see the future, despite it conflicting with the problem description. Then, one would think it looks like this (with the irrelevant "decision" node suppressed for brevity, because it's identical to the Omega's Prediction node):
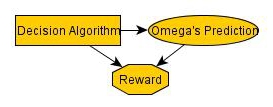
Again, we can do the same reduction:
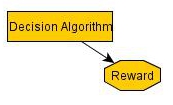
One-boxing leads to $1M, and two-boxing leads to $1k, and so one-boxing is superior to two-boxing.
*Note that this is the answer to the real question underlying the question you asked, and I suspect that almost all of the confusion surrounding Newcomb's Problem results from asking for conclusions rather than causal diagrams.
This has helped me understand much better what you were coming at in the other subthread. I disagree that CDT ought to one-box in Newcomb, at least in the "Least Convenient World" version of Newcomb that I will describe now (which I think captures the most essential features of the problem).
In this LCW version of Newcomb, quantum mechanics is false, the universe consists in atoms moving in perfectly deterministic ways, and Omega is a Laplacian superintelligence who has registered the state of each atom a million years ago and ran forward a simulation leading to a prediction on your decision. In this case none of your diagrams seem like a good causal formalization: not only does Omega not see the future magically (so your first two don't work), in addition the causal antecedent to his prediction is not your decision algorithm per se; it is a bunch of atoms a million years ago, which leads separately to his prediction on one side, and to your decision algorithm and your decision on the other side. The conflation you make in your last two diagrams between these three things, ("your decision", "your decision algorithm" and "what causally influences Omega's prediction") does not work in this case (unless you stretch your definition of "yourself" backwards to identify yourself, i.e. your decision algorithm, with some features of the distribution of atoms a million years ago!). I don't think CDT can endorse one-boxing in this case.
not only does Omega not see the future magically
In the case where the universe is deterministic and Omega is a Laplacian superintelligence, it sees the world as a four-dimensional space and has access to all of it simultaneously. It doesn't take magic- it takes the process you've explicitly given Omega!
To Omega, time is just another direction, as reversible as the others thanks to its omniscience. Saying that there could not be a causal arrow from events that occur at later times to events that occur at earlier times in the presence of Omega would be just as silly as saying that there cannot be causal arrows from events that are further to the East to events that are further to the West.
So in the LCW version of Newcomb, the first diagram perfectly describes the situation, and reduces to the second diagram. If I choose to one-box when at the button, Omega could learn that at any time it pleases by looking at the time-cube of reality. Thus, I should choose to one-box.
I disagree. I am not saying that Omega is a godlike intelligence that stands outside time and space. Omega just records the position and momentum of every atom in an initial state, feeds them into a computer, and computes a prediction for your decision. I am quite sure that with the standard meaning of "cause", here the causal diagram is:
[Initial state of atoms] ==> [Omega's computer] ==> [Prediction] ==> Money
while at the same time there is parallel chain of causation:
[Initial state of atoms] ==> [Your mental processes] ==> [Your decision] ==> {Money]
and no causal arrow goes from your decision to the prediction.
So I find it a weird use of language to say your decision is causally influencing Omega, just because Omega can infer (not see) what your decision will be. Unless you mean by "your decision" not the token, concrete mental process in your head, but the abstract Platonic algorithm that you use, which is duplicated inside Omega's simulation. But this kind of thinking seems alien to the spirit of CDT.
I disagree. I am not saying that Omega is a godlike intelligence that stands outside time and space. Omega just records the position and momentum of every atom in an initial state, feeds them into a computer, and computes a prediction for your decision.
When you say a Laplacian superintelligence, I presume I can turn to the words of Laplace:
An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.
I'm not saying that Omega is outside of time and space- it still exists in space and acts at various times- but its omniscience is complete at all times.
I am quite sure that with the standard meaning of "cause", here the causal diagram
Think of causes this way: if we change X, what also changes? If the world were such that I two-boxed, Omega would not have filled the second box. We change the world such that I one-box. This change requires a physical difference in the world, and that difference propagates both backwards and forwards in time. Thus, the result of that change is that Omega would have filled the second box. Thus, my action causes Omega's action, because Omega's action is dependent on its prediction, and its prediction is dependent on my action.
Do not import the assumption that causality cannot flow backwards in time. In the presence of Omega, that assumption is wrong, and "two-boxing" is the result of that defective assumption, not any trouble with CDT.
and no causal arrow goes from your decision to the prediction.
In your model, the only way to alter my decision, which is deterministically determined by the "initial state of atoms", is to alter the initial state of atoms. That's the node you should focus on, and it clearly causes both my decision and Omega's prediction, and so if I can alter the state of the universe such that I will be a one-boxer, I should. If I don't have that power, there's no decision problem.
Well, I think this is becoming a dispute over the definition of "cause", which is not a worthwhile topic. I agree with the substance of what you say. In my terminology, if an event X is entangled deterministically with events before it and events after it, it causes the events after it, is caused by the events before it, and (in conjunction with the laws of nature) logically implies both the events before and after it. You prefer to say that it causes all those events, prior or future, that we must change if we assume a change in X. Fine, then CDT says to one-box.
I just doubt this was the meaning of "cause" that the creators of CDT had in mind (given that it is standardly accepted that CDT two-boxes).
I just doubt this was the meaning of "cause" that the creators of CDT had in mind (given that it is standardly accepted that CDT two-boxes).
The math behind CDT does not require or imply the temporal assumption of causality, just counterfactual reasoning. I believe that two-boxing proponents of CDT are confused about Newcomb's Problem, and fall prey to broken verbal arguments instead of trusting their pictures and their math.
The math behind CDT does not require or imply the temporal assumption of causality, just counterfactual reasoning. I believe that two-boxing proponents of CDT are confused about Newcomb's Problem, and fall prey to broken verbal arguments instead of trusting their pictures and their math.
People who talk about a "CDT" that does not two box are not talking about CDT but instead talking about some other clever thing that does not happen to be CDT (or just being wrong). The very link you provide is not ambiguous on this subject.
(I am all in favour of clever alternatives to CDT. In fact, I am so in favor of them that I think they deserve their own name that doesn't give them "CDT" connotations. Because CDT two boxes and defects against its clone.)
People who talk about a "CDT" that does not two box are not talking about CDT but instead talking about some other clever thing that does not happen to be CDT (or just being wrong). The very link you provide is not ambiguous on this subject.
A solution to a decision problems has two components. The first component is reducing the problem from a natural language to math; the second component is running the numbers.
CDT's core is:
=\sum_jP(A%3EO_j)D(O_j))
Thus, when faced with a problem expressed in natural language, a CDTer needs to turn the problem into a causal graph (in order to do counterfactual reasoning correctly), and then turn that causal graph into an action which has the highest expected value.
I'm aware that Newcomb's Problem confuses other people, and so they'll make the wrong causal graph or forget to actually calculate P(A>Oj) when doing their expected value calculation. I make no defense of their mistakes, but it seems to me giving a special new name to not making mistakes is the wrong way to go about this problem.
CDT's core is:
=\sum_jP(A%3EO_j)D(O_j))
That is the math for the notion "Calculate the expected utility of a counterfactual decision". That happens to be the part of the decision theory that is most trivial to formalize as an equation. That doesn't mean you can fundamentally replace all the other parts of the theory---change the actual meaning represented by those letters---and still be talking about the same decision theory.
The possible counterfactual outcomes being multiplied and summed within CDT are just not the same thing that you advocate using.
but it seems to me giving a special new name to not making mistakes is the wrong way to go about this problem.
Using the name for a thing that is extensively studied and taught to entire populations of students to mean doing a different thing than what all those experts and their students say it means is just silly. It may be a mistake to do what they do but they do know what it is they are doing and they get to name it because they were there first.
Spohn changed his mind in 2003, and his 2012 paper is his best endorsement of one-boxing on Newcomb using CDT. Irritatingly, his explanation doesn't rely on the mathematics as heavily as it could- his NP1 obviously doesn't describe the situation because a necessary condition of NP1 is that, conditioned on the reward, your action and Omega's prediction are independent, which is false. (Hat tip to lukeprog.)
That CDTers were wrong does not mean they always will be wrong, or even that they are wrong now!
You do realise you are describing a version of CDT that almost no CDT proponent uses? It's pretty much eliezer's TDT. Now you could describe TDT as "CDT done properly" (in fact some people have described it as "EDT done properly"), but that's needlessly confusing; I'll keep using CDT to designate the old system, and TDT for the new.
You do realise you are describing a version of CDT that almost no CDT proponent uses?
Yes and no. Like I describe here, I get that most people go funny in the head when you present them with a problem where causality flows backwards in time. But the math that makes up CDT does not require its users to go funny in the head, and if they keep their wits about them, it lets them solve the problem quickly and correctly. I don't think its proponent's mistakes should discredit the math or require us to give the math a new name.
Great!
It's not clear to me that we agree about the central point of the post- I think Egan's examples are generally worthless or wrong. In the Murder Lesion, shooting is the correct decision if she doesn't have the lesion, and the incorrect decision if she does. Whether or not she should shoot depends on how likely it is that she has the lesion. He assumes that her desire to kill Alfred is enough to make the probability she has the lesion high enough to recommend not shooting- and if you stick that information into the problem, then CDT says "don't shoot." Note that choosing to shoot or not won't add or remove the lesion- and so if Mary suspects she has the lesion, she probably does so on the basis that she wouldn't be contemplating murdering Alfred without the lesion.*
In the Psychopath button, Paul can encode the statement "only a psychopath would push the button" as the statement "if I push the button, I will be a psychopath," and then CDT advises against pushing the button. (If psychopathy causes button-pushing, but the reverse is not true, then Paul should not be confident that only psychopaths would push the button!) This is similar to his 'ratifiability' idea, except instead of bolting a clunky condition onto the sleek apparatus of CDT, it just requires making a causal graph that accurately reflects the problem- and thus odd problems will have odd graphs.
In Egan's Smoking Lesion, he doesn't fully elaborate the problem, and makes a mistake: in his Smoking Lesion, smoking does cause cancer, and so CDT cautions against smoking (unless you're confident enough that you don't have the lesion that the benefits of smoking outweigh the costs, which won't be the case for those who think they have the lesion). It amazes me that he blithely states CDT's endorsement without running through the math to show that it's the endorsement!
* Edited to add: I agree that if the original Smoking Lesion problem has a "desire to smoke" variable that is a perfect indicator of the presence of the lesion, then EDT can get the problem right. The trouble should be that if the "desire to smoke" variable is only partially caused by the lesion (to the point that it's not informative enough), EDT can get lost whereas CDT will still recognize the lack of a causal arrow. I suspect, but this is a wild conjecture because I haven't run through the math yet, that EDT will set a stricter bound on "belief that I have the murder lesion" than CDT will in the version of the Murder Lesion where there's a "desire to kill" node which is partially caused by the lesion.
Ps: your graphs are very similar to mine: http://lesswrong.com/lw/f37/naive_tdt_bayes_nets_and_counterfactual_mugging/
I stumbled upon this paper by Andy Egan and thought that its main result should be shared. We have the Newcomb problem as counterexample to CDT, but that can be dismissed as being speculative or science-fictiony. In this paper, Andy Egan constructs a smoking lesion counterexample to CDT, and makes the fascinating claim that one can construct counterexamples to CDT by starting from any counterexample to EDT and modifying it systematically.
The "smoking lesion" counterexample to EDT goes like this:
EDT implies that she should not smoke (since the likely outcome in a world where she doesn't smoke is better than the likely outcome in a world where she does). CDT correctly allows her to smoke: she shouldn't care about the information revealed by her preferences.
But we can modify this problem to become a counterexample to CDT, as follows:
Here EDT correctly tells her not to smoke. CDT refuses to use her possible decision as evidence that she has the gene and tells her to smoke. But this makes her very likely to get cancer, as she is very likely to have the gene given that she smokes.
The idea behind this new example is that EDT runs into paradoxes whenever there is a common cause (G) of both some action (S) and some undesirable consequence (C). We then take that problem and modify it so that there is a common cause G of both some action (S) and of a causal relationship between that action and the undesirable consequence (S→C). This is then often a paradox of CDT.
It isn't perfect match - for instance if the gene G were common, then CDT would say not to smoke in the modified smoker's lesion. But it still seems that most EDT paradoxes can be adapted to become paradoxes of CDT.