I made a list of different evacuation routes from Berkeley that don't go through fires: https://www.facebook.com/billzito8/posts/10157744807027689
I'm curious for how long this kind of list stays current. I could imagine things having shifted after several days or a week. Just a thought for people to check before following a route here.
Ya I think people should default to assuming it's out of date, but I do plan to check it semi-regularly and edit the post to make it clear when I last looked / if things have changed. Verified the routes still made sense today (8/25) and made it clear that was when I last checked.
Timelapse of fire in the Bay Area recently. This is partway through the area covered gets twice as large. Watch the 20 seconds.
That's kind of scary and makes me feel like I maybe need to rethink my "how fast fire moves" moves. The sheer area covered is so large.
This doesn't make me panic yet, but does make me go "whoa".
Hmm. Turns out getting good comparable maps for where the fire is and has been is hard.
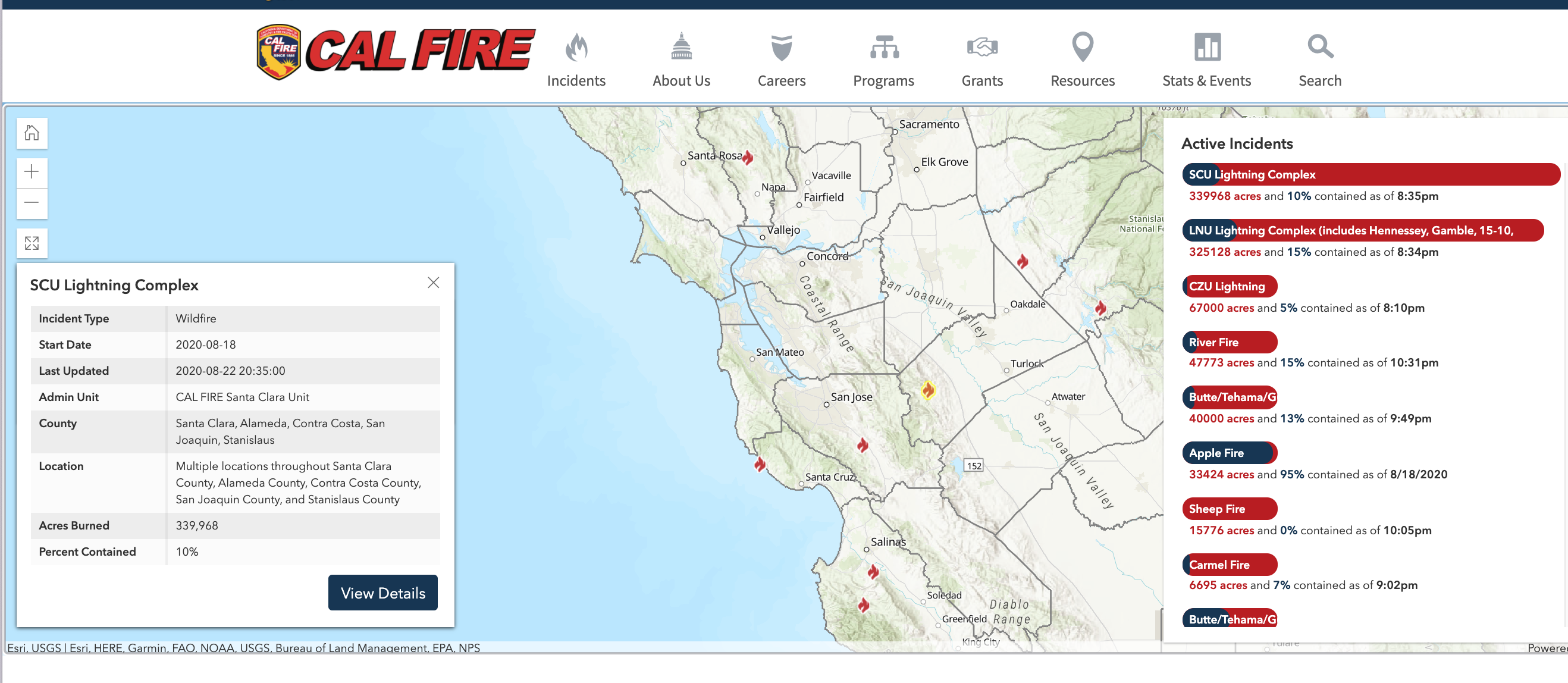
CalFire website is okay for showing where the fire currently is. See image below.
My takeaway from the current map is that currently there isn't any fire that close to SF or Berkeley/Oakland area. The "prepare to evacuate" warning for Berkeley Hill would seem to be preemptive rather than fire is already at the threshold. If you're risk-averse, I think fire in the Berkeley Hills would be your trigger to get out, with more caution the closer you live to the hills.
Not knowing more about fire than anyone else, I'd be surprised if the very large fires would actually cross so much distance to get us. Instead, I'm guessing the risk is of a fire starting up in the hills, nearby, and getting really out of control? Seems less likely.
I was beginning to make my own crappy maps to do some comparisons. The two very large fire complexes this year seem much closer to where we live than the largest fires of 2017 and 2018. See second image for 2018 fires. You can see the second image showing the major fires is zoomed out much more relative to the 2020/right now one where those massive fires are simultaneously happening close to us.
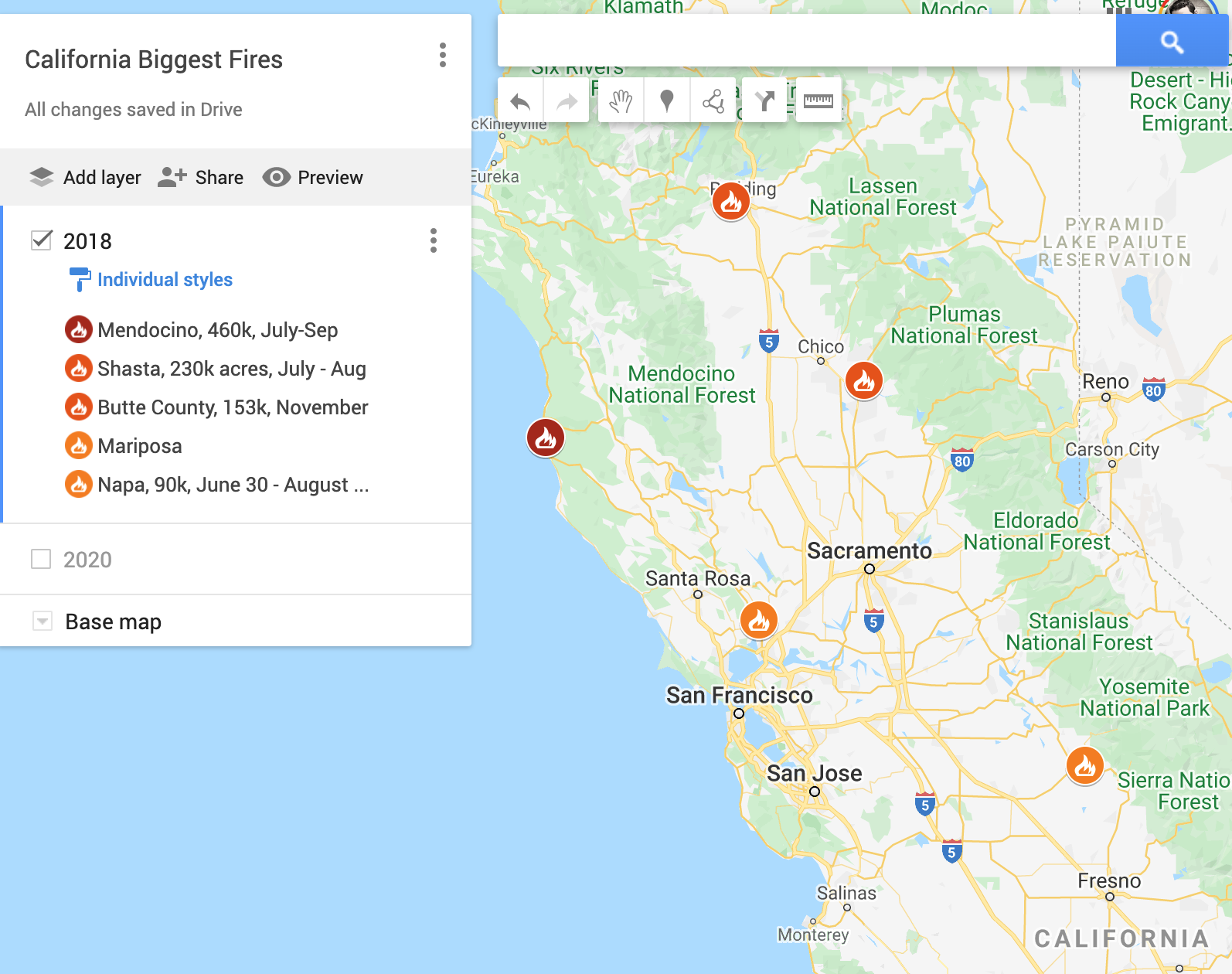
https://wildfire.cr.usgs.gov/firehistory/viewer/viewer.htm may help for historical information.
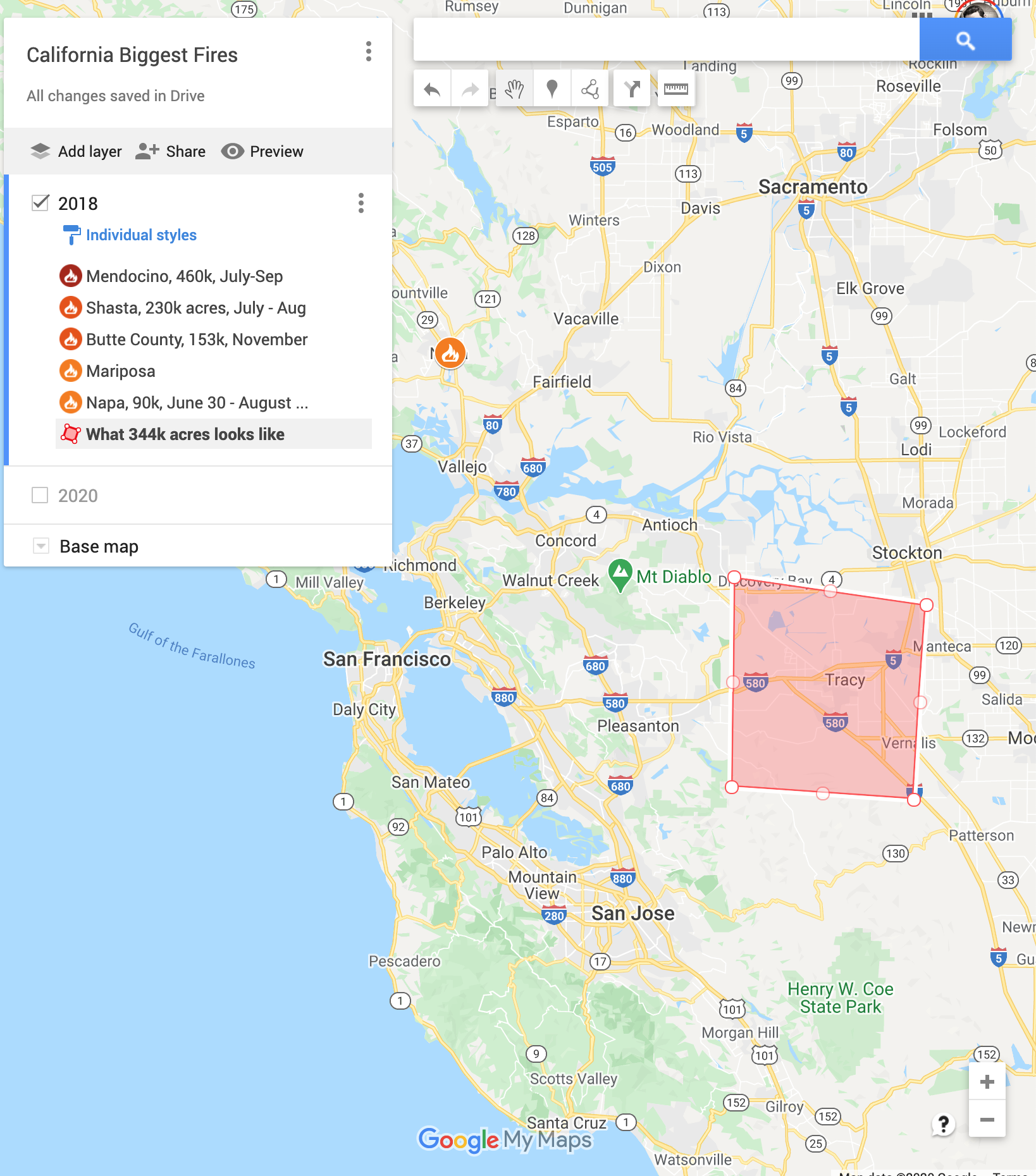
For some calibration, the red square is an area of 344k acres (location is random, obviously fires don't burn neatly in squares). Each of the two large fires of the last week have burnt apparently that much. And overall 4 such red squares have burned in like the last week.
I'm fairly sure that inmates are used mostly on long-burning fires.
Deaths directly attributed to fires seem to be almost entirely from fires that have started within an hour or so of the deaths, and those seem to be mostly handled by full-time firefighters who live near the scene.
The pandemic-induced inmate shortages might result in a modest increase in smoke from big rural fires, and that might cause more deaths via lung damage than the direct fire deaths. But a hasty evacuation is probably at least as risky as handling that via air filters.
The really unusual feature this year is the lightning. I can recall approximately zero instances of dry-season lightning in the bay area between 1994 and 2019 (although it's more normal farther inland).
Comment just to say that I've written a few more thoughts today (Monday). Writing this comment so it shows up in the newsfeed.
Worth noting, there's going to be more lightning tonight, which may or may not spark more fires
There's probably some dependence between fires in subsequent years, right? If an area burns one year, I would assume it's less likely to burn the next year. Could that explain the drop from 2018 to 2019?
I think there's so much forested area that probably doesn't explain it, also two years is probably not that much for growing back? 33 million acres of forrest in CA according to Google. So those fires burnt a lot, but also left > 90%?
Dunno.
Forest regrowth:
https://www.frontlinewildfire.com/how-forest-recovers-wildfire/
Last Updated: 2020/8/25 17:29 PDT
California currently has a lot of fire. It's not good. Some friends on a FB thread (public) were wondering whether this implied we should be doing something, e.g., leaving town. I've put in 1-2 hours of research now, and will probably do a bit more.
Notable background from the thread:
Instead of posting further updates to that Facebook thread, I'm going to make them primarily here. If you're following here from that thread, you can make an account and subscribe to this post and get emailed if I (or someone else) comments with more updates.
This isn't world-class, super-rigorous research. Just me sharing the results of some basic Googling and Wikipedia reading. Very casual.
Friday, August 21st
I did some Googling and reading, most of Wikipedia, during a long Zoom meeting today.
From a 0.5-1 hour search, this year isn't obviously going to be much worse than prior years. I was worried when one of the news articles above said last year 260k acres burnt, and this past few days we've already seen 400k burn, but actually, last year was on the very low end (see image). 2018 was the largest fire year to date and that was 1.9M acres [1].
Re firefighters: Ben Goldhaber got the number from the NYT article saying 1500/9,400 = 16% were inmates. A 2018 document from Cal Fire has it at 3500/12,200 = 29% [2]. I could see the inmate firefighters either being more or less valuable on the margin. As someone said elsethread, maybe they get used in riskier situations to greater effect, or actually, they're less well trained and get less access to the equipment like helicopters so their actual contribution is less than their proportion of the whole. I suspect the latter.
There's yet another question of how much of a difference firefighting makes. Turns out it's hard to estimate/measure. I found one detailed paper [3] looking at metrics and methodology, but my quick read didn't leave me with a strong sense of how helpful firefighting is. Maybe a factor of 2? My guess is the loss of firefighting power is on the same order of magnitude as a bunch of other variables that affect outcomes, but I'm not sure.
Tentative conclusion: things could turn out to be bad and seems worth going elsewhere if it's cheap, but so far my 0.5-1 hour investigation didn't make me think the outside view from previous years doesn't apply.
I'll try to dig in a bit more to the pattern of fires and whether there's something else that would have you predict this year is much worse than 2017 or 2018. I haven't looked at the locations of this year's fires and how that compares.
[1] https://en.wikipedia.org/wiki/List_of_California_wildfires#Post-2000
[2] https://www.fire.ca.gov/media/4922/glance.pdf
[3] sci-hub.st/10.1007/s40725-019-00085-4
Bibliography:
https://en.wikipedia.org/wiki/2018_California_wildfires
https://en.wikipedia.org/wiki/California_Department_of_Forestry_and_Fire_Protection
https://en.wikipedia.org/wiki/California_fire_camps
https://www.fire.ca.gov/stats-events/](https://www.fire.ca.gov/stats-events/
https://en.wikipedia.org/wiki/Wildfire_suppression
Saturday August 22nd
UPDATE: Changed my opinion. This year could be much worse.
Yesterday when I was comparing, I had a 400k acres number in my mind. That might have already been out of date then. Latest data [1, 2] says that already 1.4M acres have burnt. That's not quite as much as 2018 yet, but fire season last till November. I would now bet > 50% that this year will beat the record.
I don't trust journalists not to sensationalize, and I don't feel calibrated on Vox, but this [3]:
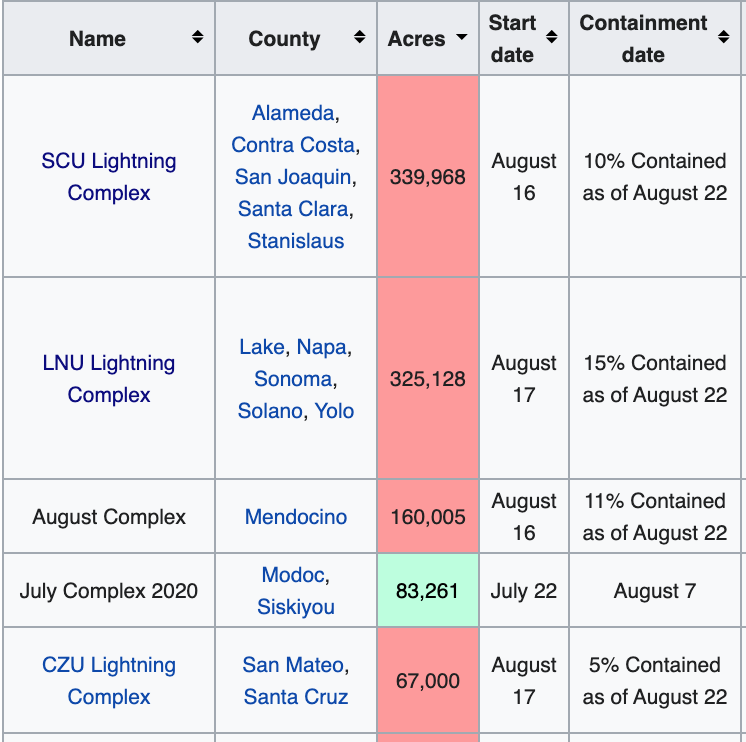
Like many (most?) things, fire size is heavy tailed. Of the 1.4M, a lot of if it just a few major fire areas, pretty much all in Northern California near the bay [2], see image. I haven't checked previous years' distribution of fire since I couldn't find maps quickly, will try to get them later. Slightly suspicion right now the big fires are closer to us than previous years, but not sure.
The top two fires here are apparently now the 2nd and 3rd largest fires on record for California.
A "be prepared to evacuate" warning has been issued to people in the Berkeley Hills. Make sense, they are right on the edge of the forest and there was fire there even in 2018 [4]
My gut feeling (and don't trust me just 'cause I found a few links) is the Hills could get affected again. How much danger that implies for someone living in Berkeley or Oakland not right near the hills is a further research question about how cities burn. [My cached answer is "not that well", but worth more investigation.]
My current thought is we should definitely be prepared for a lot of bad air. I was able to buy more air filters on Amazon, so I'd get 'em now. I'd pack a suitcase, because it's pretty cheap. I do feel motivated to research more now since I think there's enough of a chance it could be worse than previous years. I'll share more when I've got it.
[1] https://www.fire.ca.gov/incidents/2020/
[2] https://en.wikipedia.org/wiki/2020_California_wildfires#cite_note-CalFire_Stats-1
[3] https://www.vox.com/2020/8/21/21377181/california-wildfire-2020-coronavirus-covid-19-heat-scu-lnu-lightning-complex-climate
[4] https://www.berkeleyside.com/2020/08/22/red-flag-warning-for-berkeley-hills-means-residents-need-to-be-ready-to-evacuate-heres-what-you-need-to-know
Monday August 24th
Current weakly-informed opinion: assuming you don't live right in the hills, fire is very unlikely to reach your house
Caveat: I'm really not an expert here. I've spent a very small amount of time reading some things.
I took a quick look for how wildfires are fought, and found this list which I can believe is approximately how they do it: https://www.mentalfloss.com/article/57094/10-strategies-fighting-wildfires
What I take from that is cities are much easier to fight fires in than forests. Cities already have major firebreaks in the the form of roads, or even just the gaps between buildings. Fires can jump freeways, I've read, but that's got to be much harder to burning along a continuous path of fuel. That's why in forests firefighters just try to bulldoze clear paths.
I also tried to get a sense of how quickly fires move.
https://www.forbes.com/sites/startswithabang/2017/09/06/the-terrifying-physics-of-how-wildfires-spread-so-fast/amp/
Based on that, let's say a fire can move 10mi/hour. All of the very large fires burning right now are something like 50-100 mi away at least. Assuming that the fires moved straight for Berkeley Oakland (and coming from the North, they'd need to wind around in the right away), we'd still have many hours of warning. But I just would be very surprised if they moved that directly and consistently, so really I expect if it were to happen, it would take days. The danger then is that you only get the warning when everyone else does and getting out is crowded? Though I expect most people to drag their feet, so if you decided to leave as soon as the fire got anywhere near us, you'd likely be fine getting out.
The real fire risk then seems not to be the massive fires burning a distance away, but if a fire started up close to us, e.g. Berkeley Hills. That could happen, but then you'd need to count on it reaching an enormous size that couldn't be quickly stopped. I expect that if there's a fire anywhere near a metropolitan area, they will throw a lot of resources at it, on top of the fact that cities are much easier to fight fires in due the many natural firebreaks.
The counterpoint to this picture is the The Oakland Firestorm of 1991 which was pretty bad: burnt a lot of homes and killed 25 people, but if you look at the map. Due the wind (at least) it did cross an eight-lane freeway. Operations-wise seems there were delays in getting support too. The fire reached northwest edge of Montclaire and Rockridge. The fire last a day, getting contained once the wind had changed.
If I lived about the distance Rockridge is from hills, from the hills, I'd probably leave at any news of fire in the hills, expecting a < 5% (<1%?) that I then might be at risk. This seems to be about 1-2 miles (see the map below).
Living in Emeryville, as I do, I would think it's 1 in 10,000 or much less that fire would reach me from the hills, and if it was on track, I'd have a fair deal of warning that even in increased traffic, I'd expect to be fine.
Also note that because cities have roads, meaning that bringing in lots of trucks, equipment, and personnel has got to be a lot easier than in the middle of the countrside.
And lastly, cities have massive water infrastructure. Water mains with intense amounts of water. In forests, they've got helicopters picking up buckets from nearby lakes. In a city, you can just hook up to a nearby fire hydrant and spray away.
Water mains can be melted through, and in 1923 the water infrastructure didn't cope with the big fire, but I expect right now Berkeley / Oakland could put a lot of water any fire that got close.
I do expect if your house is right on the edge, the fire could get you, but for every mile you are away from the hills, I think the chances of fire getting you are increasingly slim. Like it'd take a monster fire 100x what's been seen before.
Tuesday August 25th
Timelapse of fire in the Bay Area recently. This is partway through, the area covered gets twice as large. Watch the 20 seconds.
That is kind of scary and makes me feel like I maybe need to rethink my "how fast fire moves" moves. The sheer area covered is so large.
This doesn't make me panic yet, but does make me go "whoa, I need to think more."