Let’s start with a prototypical embedded decision theory problem: we run two instances of the same “agent” from the same source code and in the same environment, and the outcome depends on the choices of both agents; both agents have full knowledge of the setup.
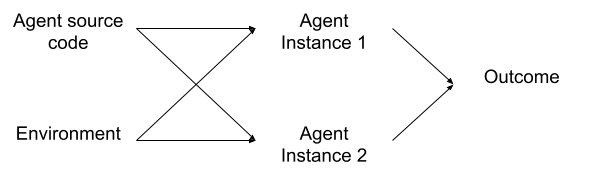
Roughly speaking, Functional decision theory and its predecessors argue that each instance of the agent should act as if it’s choosing for both.
I suspect there’s an entirely different path to a similar conclusion - a path which is motivated not prescriptively, but descriptively.
When we say that some executing code is an “agent”, that’s an abstraction. We’re abstracting away the low-level model structure (conditionals, loops, function calls, arithmetic, data structures, etc) into a high-level model. The high-level model says “this variable is set to a value which maximizes <blah>”, without saying how that value is calculated. It’s an agent abstraction: an abstraction in which the high-level model is some kind of maximizer.
Key question: when is this abstraction valid?
Abstraction = Information at a Distance talks about what it means for an abstraction to be valid. At the lowest level, validity means that the low-level and high-level models return the same answers to some class of queries. But the linked post reduces this to a simpler definition, more directly applicable to the sort of abstractions we use in real life: variables in a high-level model should contain all the information in corresponding low-level variables which is relevant “far away”. We abstract far-away stars to point masses, because the exact distribution of the mass and momentum within the star is (usually) not relevant from far away.
Or, to put it differently: an abstraction is “valid” when components of the low-level model are independent given the values of high-level variables. The roiling of plasmas within far-apart stars is (approximately) independent given the total mass, momentum, and center-of-mass position of each star. As long as this condition holds, we can use the abstract model to correctly answer questions about things far away/far apart.
Back to embedded decision theory.
We want to draw a box around some executing code, and abstract all those low-level operations into a high-level “agent” model - some sort of abstract optimizer. The only information retained by the high-level model is the functional form of the abstracted operations - the overall input-output behavior, represented as “<output> maximizes <objective> at <input>”. All the details of the calculation are thrown out.
Thing is, those low-level details of the calculation structure? They’re exactly the same for both instances of our agent. (Note: the structure is the same, not necessarily the variable values; this argument assumes that the structure itself is a “variable”. If this is confusing, imagine that instead of two instances of the same source code running on a computer, we’re talking about two organisms of the same species - so the genome of one contains information about the genome of the other.) So if we draw a box around just one of the two instances, then those low-level calculation details we threw out will not actually be independent of the low-level calculation details in the other instance. The low-level structure of the two components - the two agent instances - is not independent given the high-level model; the abstraction is not valid.
On the other hand, if we draw a box around both instances (along with the source code), and apply an agent abstraction to both of them together… that can work. The system still needs to actually maximize some objective(s) - we can’t just draw a box around all instances of some random python script and declare it to be maximizing a particular function of the outcome - but we at least won’t run into the problem of correlated low-level structure between abstract components. The abstraction won’t leak in the same way.
Summarizing: we need to draw our box around both instances of the agent because if we only include one instance, then the agent-abstraction leaks. Any abstract model of just one agent-instance as maximizing some objective function of the outcome would be an invalid abstraction.
Glaring Problems
This setup has some huge glaring holes.
First and foremost: why do we care about validity of queries on correlations between the low-level internal structures of the two agent-instances? Isn’t the functional behavior all that’s relevant to the outcome? Why care about anything irrelevant to the outcome?
One response to this is that we don’t want the agent to “know” about its own functional behavior, because then we run into diagonalization problems and logical uncertainty gets dragged in and so forth. We want to treat the functional behavior as unknown-to-the-agent, which means the (known) correlation between low-level behaviors contains important information about correlation between high-level behaviors.
That’s hand-wavy, and I’m not really satisfied with what the hands are waving at. Ideally, I’d like an approach which doesn’t explicitly drag in logical uncertainty until much later, even if that is a correct way to think about the problem. I suspect there’s a way to do this by reformulating the interventions as explicitly throwing away information about the agent’s functional behavior, and replacing it with other information. But I haven’t fleshed that out yet.
Ultimately, at this point the approach looks promising largely on the basis of pattern-matching, and I don’t yet see why this particular abstraction-validity matters. It’s honestly kind of embarrassing.
Anyway, second problem: What if two instances wound up performing the same function due to convergent evolution, without any correlation between their low-level structures? Abram has written about this before: roughly speaking, he’s argued that embedded decision theory should be concerned about cases where two agents’ behavior is correlated for a reason, not necessarily cases where we just happen to have two agents with exactly the same code. It was a pretty good argument, and I’ll defer to him on that one.
Upside
We’ve just discussed what I see as the main barriers to making this approach feasible, and they’re not minor. And even with those barriers handled, there’s still a lot of work to properly formalize all this. So what’s the upside? Why pursue an abstraction-first decision theory?
The main potential is that we can replace fuzzy, conceptual questions about what an agent “should” do with concrete questions about when and whether a particular abstraction is valid. Instead of asking “Is this optimal?” we ask “If we abstract this subsystem into a high-level agent maximizing this objective, is that abstraction valid?”. Some examples:
- “Is my decision process actually optimal right now?” becomes “Is this agent abstraction actually valid right now?”
- “In what situations does this perform optimally?” becomes “In what situations is this agent abstraction valid?”
- “How can we make this system perform optimally in more situations?” becomes “How can we make this agent abstraction valid in more situations?”
In all cases, we remove “optimality” from the question. More precisely, an abstraction-first approach would fix a notion of optimality upfront (in defining the agent abstraction), then look at whether the agent abstraction implied by that notion of optimality is actually valid.
Under other approaches to embedded decision theory, a core difficulty is figuring out what notion of “optimality” to use in the first place. For instance, there’s the argument that one should cooperate in a prisoner’s dilemma when playing against a perfect copy of oneself. That action is “optimal” under an entirely different set of “possible choices” than the usual Nash equilibrium model.
So that’s one big potential upside.
The other potential upside of an abstraction-first approach is that it would hopefully integrate nicely with abstraction-first notions of map-territory correspondence. I’ll probably write another post on that topic at some point, but here’s the short version: straightforward notions of map-territory correspondence in terms of information compression or predictive power don’t really play well with abstraction. Abstraction is inherently about throwing away information we don’t care about, while map-territory correspondence is inherently about keeping and using all available information. A New York City subway map is intentionally a lossy representation of the territory, it’s obviously throwing out predictively-relevant information, yet it’s still “correct” in some important sense.
“Components of the low level model are independent given the corresponding high-level variables” is the most useful formulation I’ve yet found of abstraction-friendly correspondence. An abstraction-first decision theory would fit naturally with that notion of correspondence, or something like it. In particular, this formulation makes it immediately obvious why an agent would sometimes want to randomize its actions: randomization may be necessary to make the low-level details of one agent-instance independent of another, so that the desired abstraction is valid.