Bayesians are updating too much on AI capability speed from this data point, given:
- The CI is extremely wide and METR's own caveats about sparsity at higher horizons.
- This level of a jump relative to the previous Opus 4.1 or Opus 4 is inconsistent with the 80% success threshold, accuracy level, and other key benchmarks that should correlate with capabilities (ECI, swe-bench bash).
I modeled all this in GPT-5.2 and the more realistic estimate for 50% derived from the other benchmarks is in the range of 190 to 210 minutes, depending on how much weight you put on the impressive (but not to the degree of the 50%) accuracy jump. The 80% is likely a slight underestimate (my guess is closer to 29 minutes).
These numbers:
- Maps to around a 15-20th percentile on the CI interval for the 50% and a 60th percentile for the 80%, in the realms of "this is due to chance". [1]
- Gives around a 5-6 month doubling relative to Opus 4 and a 6-7 month doubling relative to O3.
- Imply evidence for the 50% - 80% capabilities systemically widening is weak.
[1] Note that this does provide evidence that Gemini 3 and GPT-5.2 will also have high p50 scores. Not because of capability jump per se but because of the distribution of tasks within METR benchmarks.
Could you share your model, if you haven't modeled it in an incognito chat? And don't forget to check out my comment below. If you are right, then the alternate Claude who succeeded at 15-second-long tasks would have a lower 50% time horizon.
P.S. I also asked the AIs a similar question. Grok 4 failed to answer, Gemini 3 Pro estimated the revised 80% horizon as 35-40 mins and the 50% horizon as 6-7 hrs. GPT-5's free version gave me this piece of slop, EDIT: Claude Opus 4.5 estimated the revised 80% horizons at 30-45 or 45-60 mins and 50% horizons as 2-3 hrs or 3-4 hrs.
Private workspace so I can’t share the session. But the approach is simple and doesn’t really require it to understand.
I think we’re coming at this from different angles: you’re doing a “white-box” critique (how specific task outcomes / curve fitting affect the METR horizon), whereas I’m doing a “black-box” consistency check: is the claimed p50 result consistent with what we see on other benchmarks that should correlate with capability?
The core model is:
- Take Sonnet 4 → Sonnet 4.5 and compute the improvement rate (slope).
- Assume Opus improves at the same rate as Sonnet over this period.
- Start from Opus 4 as the anchor and ask: “when would we expect to reach the Opus 4.5 reported value?”
(For METR horizons I do this in log space; for accuracy/ECI I treat it as linear.)
That yields “time ahead/behind” vs the reported Opus 4.5 result:
- ECI: ~1.3 months ahead
- SWE-bench bash agent: on target (about a week behind)
- METR accuracy: ~2.4 months ahead
- METR 80% horizon: ~1 month behind
- METR 50% horizon (using METR’s reported 289 min): ~4.5 months ahead
The point is that METR p50 is the outlier relative to the other signals.
If instead we assume Opus 4.5 is only as far “ahead” as the other benchmarks suggest, then p50 should be closer to:
- 1.3 months ahead (ECI-like): ~200 minutes
- 2.4 months ahead (accuracy-like): ~226 minutes
And the corresponding implied p80 would be:
- on-target: ~28 minutes
- 1.3 months ahead: ~30 minutes
- 2.4 months ahead: ~32 minutes
My best guess is we’re ~1 month ahead overall, which puts p50/p80 in-between those cases.
Finally, percentiles inside METR’s CI depend on the (unstated) sampling distribution; if you approximate it as log-normal you get the rough “position within the CI” numbers I mentioned, but it’s only an approximation.
Well, guess I was wrong.
(I’ll probably lose my bet with @Daniel Kokotajlo that horizon lengths plateau before 8 hours)
https://www.lesswrong.com/posts/2RwDgMXo6nh42egoC/how-to-game-the-metr-plot
Claude's performance is low on the 2-4 hour range, which mostly consists of cybersecurity tasks, potentially dual-use for safety. In general, training on cybersecurity CTFs and ML code would increase "horizon length" on the METR plot, which only has 14 samples in the relevant (1 - 4hr) range where progress happened in 2025.
If I'm intrepreting these charts correctly, there is a decent amount of progress in 15m-1hr bracket, a small amount of progress in the 1hr bracket, a decent amount of progress in the 2-4 hr bracket, and a large amount of progress in the 4-16hr bracket. It doesn't look like progress was dominated by the 1-4hr range.
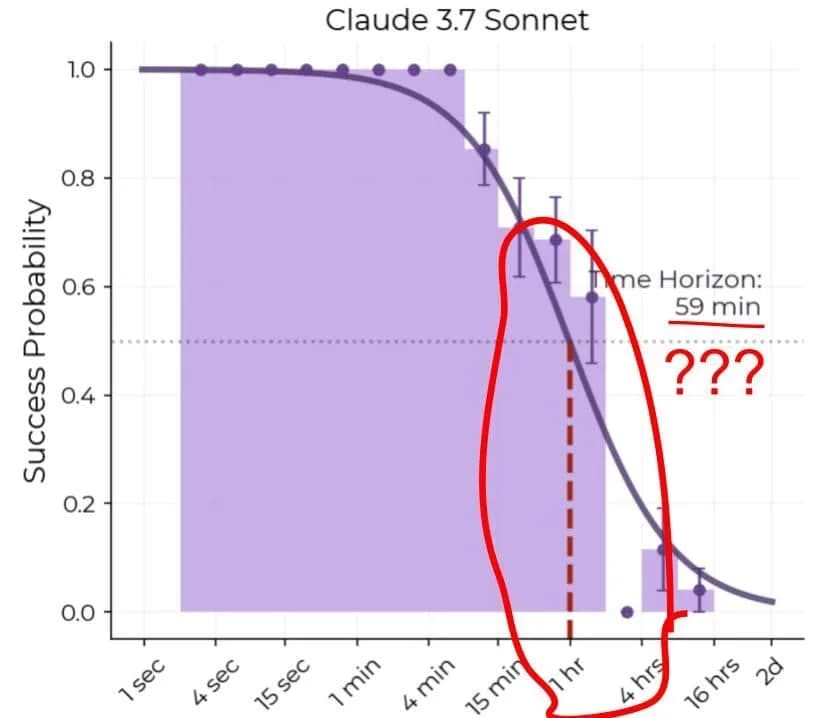
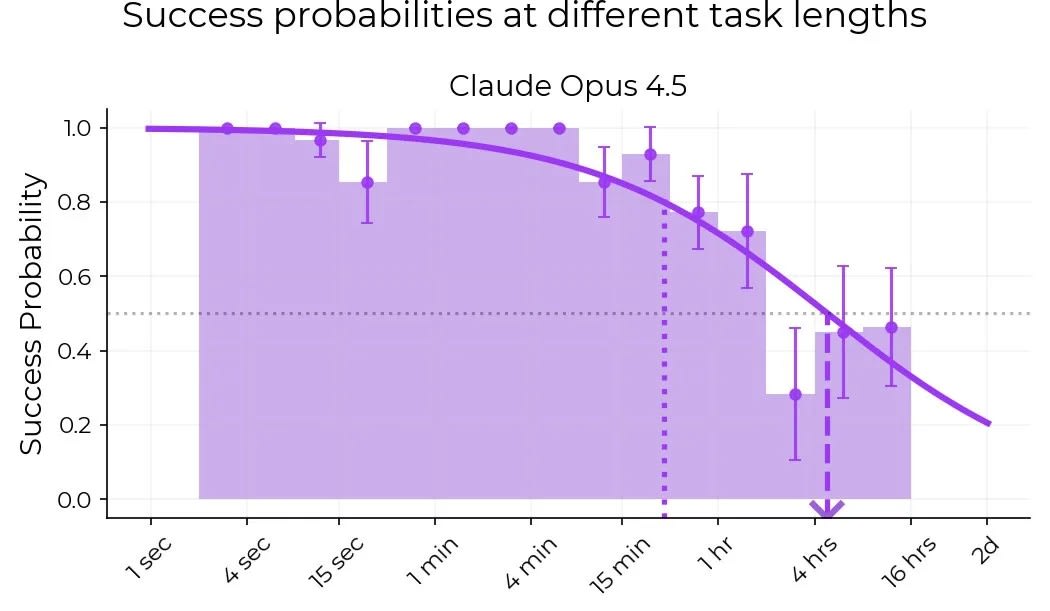
The mean estimate of 50% success horizon length (headline number METR reports) went from ~1 to ~4 hours. The progress within the hour subranges is difficult to draw much information from, given the low number of data points, and distribution biases in topics. This is the precise claim of the new post I made, and linked :)
I have read your link and I understand you seem to have much more knowledge about statistics than I am. Perhaps I'm making a simple mistake somewhere in my reasoning. My thoughts are:
50 success horizon went from 1 to 4 hours. I interpreted your comment and post to posit that the increase is to some large degree due to training on cybersecurity to increase preformance in the 2-4hr range. However, looking at the charts it seems clear that the increase is not dominated by increased preformance in the 2-4hr range.
My point isn't that there's enough samples or that it isn't possible to game the METR test, it's that the measured improvement for Claude Opus 4.5 doesn't seem to be primarly in the 2-4 hr bracket, if anything it's dominated by 4-16hr.
I personally think the stronger argument here is that Claude models are not growing in capability consistent with higher task length = harder. (Grok 4 was similar) if you look at the histograms.
Both Sonnet 4.5 and Opus 4.5 were outperforming in the 8 to 16 hour bracket over the 2 to 4 hour, which is highly inconsistent with the task length difficulty model. The model appears broken at last since 3.5 sonnet given the flatness of the 2-16 hour tasks.
You end up in a case where the 4.5 Sonnet curve has a higher % of the solved tasks under it than 4.5 Opus (note how 4.5 Opus gets 0 tasks right in the 16 hour to 32 hour window even though the distribution implies it should be more like 25%). That is the "gain" this implies is overstated dramatically. [1]
The unfortunate consequence is largely shash42's point - it's not clear that modeling "task length horizon" is a valid way to view this data. Raw accuracy seems better correlated with time.
[1] An alternative interpretation is that Sonnet 4.5 was much better than the METR curve then implied.
This makes me think of the previous model with the biggest 50%/80% time horizon ratio, Grok 4. It had funny failures at 2 sec, 2min and 2h long tasks. What if an alternate-universe Claude who, like GPT-5.1-Codex-Max, succeeded at ALL tasks shorter than a minute, would have achieved a far bigger 80% time horizon? And if GPT-5.2 and Gemini 3 Pro had the failures at less-than-a-minute-long tasks ironed out, as happened with GPT-5 vs Grok 4?
EDIT: in theory, the alternate Claude could also end up with a worse 50% time horizon. But the real Claude succeeded on a quarter of 2-4 hr long tasks and about a half of 4-16 hr long tasks.
Yes, both model families are similar in that they do not have consistently declining accuracy in the 2-16 hour task window. The modeling is somewhat broken when you have higher accuracy in the 8-16 hour window than the 2-4 hour window.
GPT models do not have this characteristic; while not perfect with the curve, at least accuracy roughly drops monotonically with task length. (exception o4-mini which also had bizarre patterns in that 2-16 hour window).
I suspect at some level heavy RLVF has broken the core METR model of performance correlating to task length.
The flat 80%-horizon while 50%-horizon climbs might be evidence for intercept-dominated progress.
@Michaël Trazzi Actually, it's the opposite, the Claude progress was dominated by slope () improvement, and intercept actually got a bit worse: Is METR Underestimating LLM Time Horizons?
An updated METR graph including Claude Opus 4.5 was just published 3 hours ago on X by METR (source):
Same graph but without the log (source):
Thread from METR on X (source):
The 80%-horizon has stayed essentially flat (27-32 mins) since GPT-5.1-Codex-Max's release but there's a big jump with huge error bars on the 50%-horizons.
I think Daniel Kokotajlo's recent shortform offers a useful framing here. He models progress as increasing either the intercept (baseline performance) or the slope (how well models convert time budget into performance). If progress comes mainly from rising intercepts, an exponential fit to horizon length could hold indefinitely. But if progress comes from increasing slope, the crossover point eventually shoots to infinity as AI slope approaches human slope.
The flat 80%-horizon while 50%-horizon climbs might be evidence for intercept-dominated progress.