Previously in series: Mach's Principle: Anti-Epiphenomenal Physics
Followup to: Classical Configuration Spaces
Warning: The ideas in today's post are taken seriously by serious physicists, but they are not experimentally proven and are not taught as standard physics.
Today's post draws on the work of the physicist Julian Barbour, and contains diagrams stolen and/or modified from his book "The End of Time".
Previously, we saw Mach's idea (following in the earlier path of Leibniz) that inertia is resistance to relative motion. So that, if the whole universe was rotating, it would drag the inertial frame along with it. From the perspective of General Relativity, the rotating matter would generate gravitational waves.
All right: It's possible that you can't tell if the universe is rotating, because the laws of gravitation may be set up to make it look the same either way. But even if this turns out to be the case, it may not yet seem impossible to imagine that things could have been otherwise.
To expose Mach's Principle directly, we turn to Julian Barbour.
The diagrams that follow are stolen from Julian Barbour's The End of Time. I'd forgotten what an amazing book this was, or I would have stolen diagrams from it earlier to explain configuration space. Anyone interested in the nature of reality must read this book. Anyone interested in understanding modern quantum mechanics should read this book. "Must" and "should" are defined as in RFC 2119.
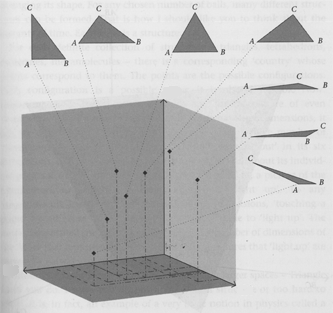 Suppose that we have three particles, A, B, and C, on a 2-dimensional plane; and suppose that these are the only 3 particles in the universe.
Suppose that we have three particles, A, B, and C, on a 2-dimensional plane; and suppose that these are the only 3 particles in the universe.
Let there be a classical configuration space which describes the 2D positions of A, B, and C. 3 classical 2D particles require a 6-dimensional configuration space.
If your monitor cannot display 6-dimensional space, I've set a 2D projection of a 3D cube to appear instead. If you see what looks like a window into an incomprehensible void, try using Firefox instead of Internet Explorer.
The thing about this 6-dimensional cube, is that it contains too much information. By looking at an exact point in this cube—supposedly corresponding to an exact state of reality—we can read off information that A, B, and C will never be able to observe.
The point (0, 1, 3, 4, 2, 5) corresponds to A at (0, 1), B at (3, 4), and C at (2, 5). Now consider the point (1, 1, 4, 4, 3, 5); which corresponds to moving A, B, and C one unit to the right, in unison.
Can A, B, and C ever detect any experimental difference? Supposing that A, B, and C can only see each other, as opposed to seeing "absolute space" in the background?
After we shift the universe to the right (shift the origin to the left), A looks around... and sees B and C at the same distance from itself as before. B and C can't detect any difference in the universe either.
Yet we have described (0, 1, 3, 4, 2, 5) and (1, 1, 4, 4, 3, 5) as two different points in the configuration space. Even though, to A, B, and C, the associated states of reality seem indistinguishable. We have postulated an epiphenomenal difference: This suggests that our physics is not over the true elements of reality. (Remember, this has been, historically, a highly productive line of reasoning! It is not just logic-chopping.)
Indeed, our classical configuration space has many epiphenomenal differences. We can rotate the three particles in unison, and end up with a different point in the configuration space; while A, B, and C again see themselves at the same distances from each other. The "rotation" that took place, was a matter of us looking at them from a different angle, from outside their universe. Which is to say the "rotation" was a choice of viewpoint for us, not an experimentally detectable fact within the ABC universe.
How can we rid the physics of mind projections and epiphenomena?
A and B and C cannot observe their absolute positions in space against a fixed background. Treating these absolute positions as elements of reality may be part of our problem.
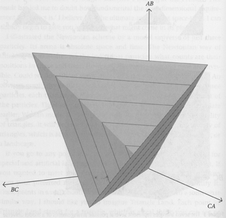 What can A, B, and C observe? By hypothesis, they can observe their distances from each other. They can measure the distances AB, BC, and CA.
What can A, B, and C observe? By hypothesis, they can observe their distances from each other. They can measure the distances AB, BC, and CA.
Why not use that as the dimensions of a configuration space?
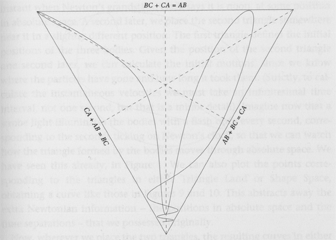
At right is depicted a relative configuration space whose three dimensions are the distances AB, BC, and CA. It really is 3-dimensional, now!
If you're wondering why the configuration space looks pyramidal, it's because any point with e.g. AB + BC < CA is "outside the configuration space". It does not represent a realizable triangle, because one side is longer than the sum of the other two. Likewise AB + CA < BC and BC + CA < AB.
Every different point in this configuration space, corresponds to an experimentally different state of reality that A, B, and C can observe.
 (Albeit this assumes that ABC can measure absolute, rather than relative, distances. Otherwise, different slices of pyramid-space would be observationally identical because they would describe the same triangle at different scales, as shown at left.)
(Albeit this assumes that ABC can measure absolute, rather than relative, distances. Otherwise, different slices of pyramid-space would be observationally identical because they would describe the same triangle at different scales, as shown at left.)
(Oh, and we're assuming that A, B, and C can tell each other apart—perhaps they are different colors.)
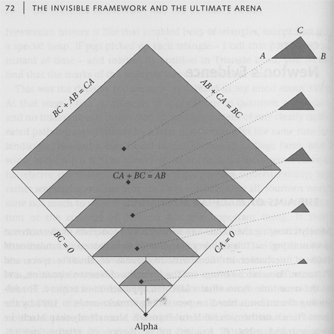
The edges of each slice of the configuration space, are the configurations with A, B, and C on the same line. E.g., if AB + BC = CA, then B lies on a point between A and C.
The corners of each slice are the configurations in which two points coincide; e.g., AB=0, BC=CA.
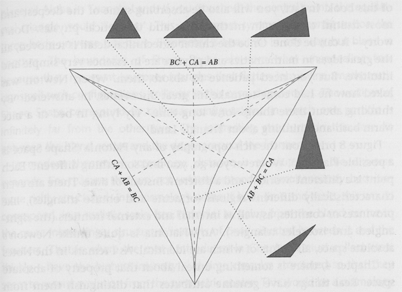 At right (or possibly below, depending on your screen width), is a diagram showing a single slice in greater detail; Julian Barbour credits this to his friend Dierck Liebscher.
At right (or possibly below, depending on your screen width), is a diagram showing a single slice in greater detail; Julian Barbour credits this to his friend Dierck Liebscher.
The point in the center of the slice corresponds to an equilateral triangle.
The dashed lines, which are axes of bilateral symmetry of the configuration space, contain points that correspond to isosceles triangles.
The curved lines are right-angled triangles.
Points "inside" the curved lines are acute triangles; points "outside" the curved lines are obtuse triangles.
What about three points coinciding?
There is no triangle at this scale where all three points coincide.
Remember, this is just one slice of the configuration space. Every point in the whole configuration space corresponds to what ABC experience as a different state of affairs.
The configuration where A, B, and C are all in the same place is unique in their experience. So it is only found in one slice of the configuration space: The slice that is a single point, at the tip of the infinite pyramid: The degenerate slice where the center and the corners are the same point: The slice that is the single point in configuration space: AB=BC=CA=0.
Julian Barbour calls this point Alpha.
But I'm getting ahead of myself, here—that sort of thing is the topic of tomorrow's post.
To see the power of a relative configuration space, observe how it makes it impossible to imagine certain epiphenomenal differences:
Put your Newtonian goggles back on: imagine A, B, and C as little billiard balls bouncing around in plain old space (not configuration space) and time. Perhaps A, B, and C attract each other via a kind of gravity, and so orbit around one another. If you were looking at the evolution of A, B, and C in plain old space and time, then a strobe-lit photograph of their motion might look like this:
In this time-series photograph, we've seen points A, B, and C forming a triangle. Not only do the points of the triangle orbit around each other, but they also seem to be heading down and to the right. It seems like you can imagine the triangle heading off up and to the right, or up and to the left, or perhaps spinning around much faster. Even though A, B, and C, who can only see their distance to each other, would never notice the difference.
Now we could also map that whole trajectory over time, onto the relative configuration space. If AB+BC+CA happens to be a constant throughout the evolution, then we could conveniently map the trajectory onto one slice of configuration space:
(This doesn't actually represent the triangle-series shown above it, but imagine that it does.)
If this is what you believe to be the reality—this trajectory in the relative configuration space—then, if I ask you to imagine, "Suppose that the triangle is heading up and to the left, instead of down and to the right", I have just uttered physical nonsense. Mapping that alternative trajectory in Newtonian space, onto the relative configuration space, would produce just the same curve. And if the laws of physics are over the relative configuration space, then this curve is all there is.
Imagine physics over trajectories in a relative configuration space like this one, but with many more particles, and perhaps 3 space dimensions. Sentient beings evolve in this universe, on some equivalent of a planet. They hunt across fields that do not seem to shift underfoot. They have a strong illusion of moving through an absolute space, against an absolute background; the relativity of motion is hidden from them.
But if the fundamental laws of their universe were over relative configurations, then it would not just be a contingent fact about their universe, that if all the particles were speeding or accelerating or rotating in unison, all the experiments would come out the same. Talking about "all the particles rotating in unison" would be physical nonsense. It only makes physical sense to talk about the velocity of some particles relative to other particles.
Your ancestors evolved on a savanna that seemed to stay put while they ran across it. You can, by an effort of mind, visualize a car that stays motionless as the world zips past, or alternatively, visualize a world that remains motionless as the car zips past. You can, by an effort of mind, see that the internal relations are the same. But it still seems to you that you are imagining two different things.
Your visual neurology is representing objects in terms of absolute positions against a fixed background. There is a web of cortical columns in your visual cortex that activate to create a mental picture. The particular columns that activate, are felt by you as positions in your visual field. That is how the algorithm feels from inside.
In a universe whose physics is over a relative configuration space, the absolute positions, and the fixed background, are not elements of reality. They are mind projection fallacies, the shadows of a point of view; as if your mind's eye were outside the universe, and the universe could move relative to that.
But if you could learn to visualize the relative configuration space, then, so long as you thought in terms of those elements of reality, it would no longer be imaginable that Mach's Principle could be false.
I am not entirely convinced of this notion of a relative configuration space. My soul as a computer programmer cries out against the idea of representing N particles with N2 distances between them; it seems wasteful. On the other hand, I have no evidence that the Tao is prejudiced against redundant or overconstrained representations, in the same way that the Tao seems prejudiced against epiphenomena in representations. Though my soul as a programmer cries out against it, better an overconstrained representation than an epiphenomenal one. Still, it does not feel entirely satisfactory, to me. It seems like merely the best representation, not the true one.
Also, any position basis invokes an arbitrary space of simultaneity, and a relative position basis does so as well. As required by Special Relativity, the choice makes no difference—but this means that the relative position basis still contains epiphenomenal information. Perhaps the true representation will be more strictly local, in terms of invariant states of distant entanglement, as I've suggested before; and maybe, who knows, it won't be overconstrained?
Relativizing the position basis feels to me like an improvement, but it doesn't seem finished.
...
Of course, all this that we have said about the particles A, B, C and their trajectory through time, cannot possibly apply to our own universe.
In our own universe, as you may recall, there are no little billiard balls bouncing around.
In our own universe, if physics took place in a relative configuration space, it would be quantum physics in a relative configuration space. And a single moment of time, might look like this:
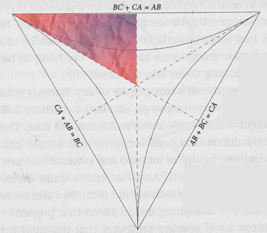 At right we see a cloud of red and blue mist, representing a complex amplitude distribution over the relative configuration space. You could imagine that redness is the real part and blueness is the imaginary part, or some such. But this is not a realistic amplitude distribution—just a representation of the general idea, "A cloud of complex amplitude in configuration space."
At right we see a cloud of red and blue mist, representing a complex amplitude distribution over the relative configuration space. You could imagine that redness is the real part and blueness is the imaginary part, or some such. But this is not a realistic amplitude distribution—just a representation of the general idea, "A cloud of complex amplitude in configuration space."
As for why only a sixth of the triangle is colored: If A, B, and C are the same species of particle, which is to say, identical particles, then the configuration space collapses along the sixfold symmetry corresponding to the six possible permutations of A, B, and C.
The whole cloud is a single static instant, in some arbitrary space of simultaneity. The quantum wavefunction is a distribution over configuration space, not a single point in configuration space. So to represent the state of the universe at a single moment, we need the whole cloud, which covers the entire collapsed configuration space.
You might naturally tend to assume that we could represent time using an animated version of this same diagram: and that the animated diagram would show the mist churning in the configuration space, the cloud's parts changing color, as amplitude flowed from volume to volume; and that as the quantum waves propagated, little blobs of amplitude density would move around through the configuration space, in trajectories much resembling the classical curve we saw earlier.
But that would be overcomplicating things.
Be aware: Churning mist in a non-relative configuration space, would be the metaphor that corresponds to the standard formulation of physics. That is, according to standard physics, the description I just gave above, would be correct (after we took it back out of the relative configuration space, which is not standard).
Yet tomorrow we shall discuss a certain further simplification of physics, which renders unimaginable still another epiphenomenal distinction, and deletes a further needless element of the laws.
Part of The Quantum Physics Sequence
Next post: "Timeless Physics"
Previous post: "Mach's Principle: Anti-Epiphenomenal Physics"