When we train Sparse Autoencoders (SAEs), the sparsity of the SAE, called L0 (the number of latents that fire on average), is treated as an arbitrary design choice. All SAE architectures include plots of L0 vs reconstruction, as if any choice of L0 is equally valid.
However, recent work that goes beyond just calculating sparsity vs reconstruction curves shows the same trend: low L0 SAEs learn the wrong features [1][2].
In this post, we investigate this phenomenon in a toy model with correlated features and show the following:
- If the L0 of the SAE is lower than the true L0 of the underlying features, the SAE will "cheat" to get a better MSE loss score than a correct SAE would achieve by learning broken mixtures of correlated features. This can be viewed as a form of feature hedging[3]. This is worse the lower the L0 of the SAE, and affects high-frequency features more severely.
- If the L0 of the SAE is higher than the true L0 of the underlying features, the SAE will find degenerate solutions, but does not engage in feature hedging. This is worse the higher the L0 of the SAE.
- If we mix together a too-low L0 loss with a too-high-L0 loss, we can learn the true features (like a Matryoshka SAE[2], except with multiple L0s instead of multiple widths). This may provide a way to learn a correct SAE despite not knowing the "true L0" of the underlying training data.
The phenomenon of poor performance due to incorrect L0 can be viewed from the same lens of Feature Hedging: If we do not give SAEs enough resources in terms of L0 or width to reconstruct the input, the SAE will find ways to cheat by learning incorrect features. In light of this, we feel that L0 should not be viewed as an arbitrary hyperparameter. We should assume that there is a "correct" L0, and we should aim to find it.
In the remainder of this post, we will walk through our experiments and results. Code is available in this Colab Notebook.
Toy model setup
We set up a toy model with 20 mutually-orthogonal true features through , where features 1-19 are positively correlated with . For each of these features, we assign a base firing probability . Feature fires with probability if feature 0 is firing, and probability if is not firing. Thus, each feature can fire on its own, but is more likely to fire if is also firing. Feature fires with probability , and through linearly decreases from to , so that is more likely to fire overall than , and is more likely to fire than , etc... To keep everything simple, each feature fires with mean magnitude and stddev . The stddev is needed to keep the SAE for engaging in Feature Absorption[4], as studying absorption is not the goal of this exploration.
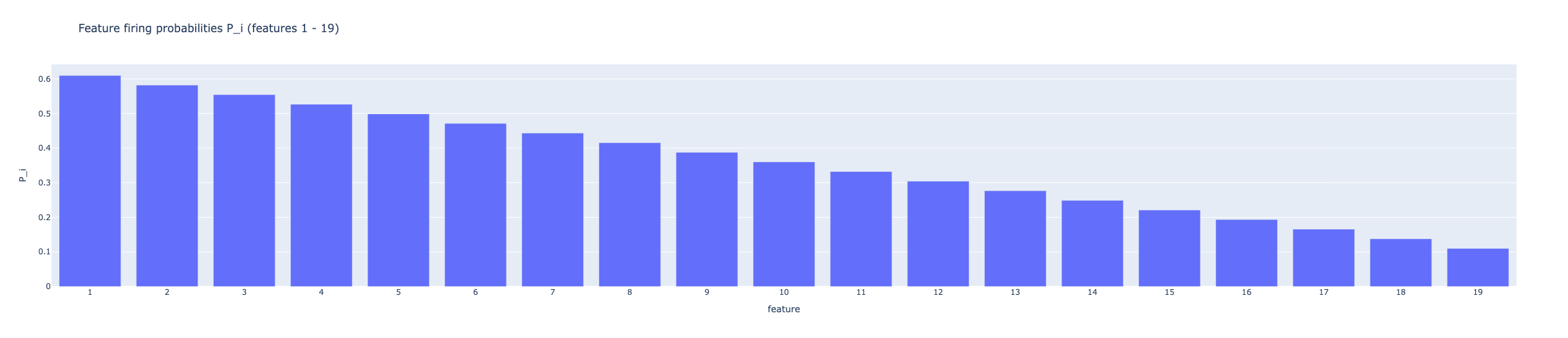
These probabilities were chosen so the true L0 (the average number of features active per sample) is roughly 5.
SAE setup
We use a Global BatchTopK SAE[5] with the same number of latents (20) as the number of features in our toy model. We use a BatchTopK SAE to allow us to control the L0 of the SAE directly so we can study the effect of L0 in isolation of everything else. The SAE is trained on 25 Million samples generated from the toy model.
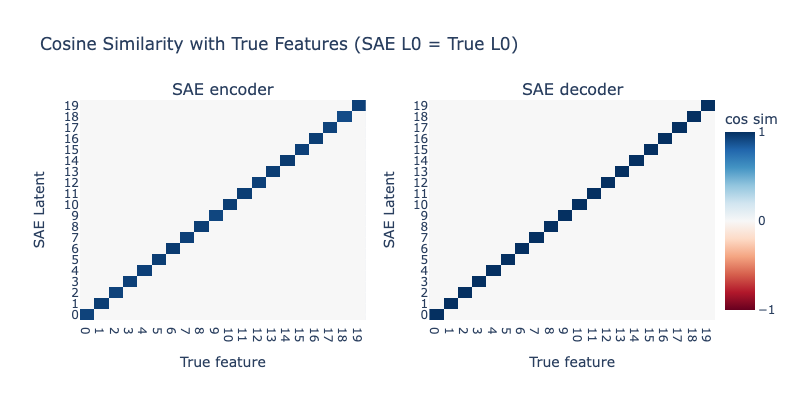
Case 1: SAE L0 = Toy Model L0
We begin by setting the L0 of the SAE to 5 to match the L0 of the underlying toy model. As we would hope, the SAE perfectly learns the true features.
Case 2: SAE L0 < Toy Model L0
Next, we set the L0 of the SAE to 4, just below the correct L0 of 5. The results are shown below:
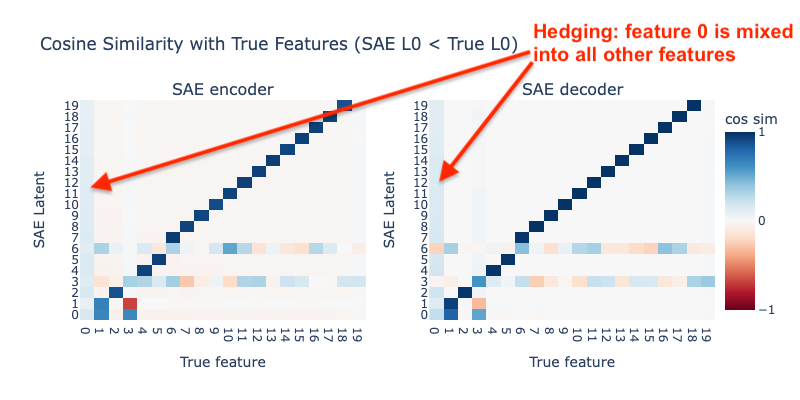
We now see clear signs of hedging: the SAE has decided to mix into all other latents to avoid needing to represent it in its own latent. In addition, the latents tracking high-frequency features (features 1-5) appear much more broken than latents tracking lower-frequency latents.
Cheating improves MSE loss
Why would the SAE do this? Why not still learn the correct latents, and just fire 4 of them instead of 5? Below, we calculate the mean MSE loss from using the correct SAE from Case 1, except selecting the top 4 instead of 5 features, with the broken SAE we trained in Case 2.
| MSE loss | |
| Case 1 (correct) SAE, trained with k=5 and cut to k=4 | 0.53 |
| Case 2 (broken) SAE, trained with k=4 | 0.42 |
Sadly, the broken behavior we see above achieves better MSE loss than correctly learning the underlying features. We are actively incentivizing the SAE to engage in feature hedging and learn broken latents when the SAE L0 is too low.
Lowering SAE L0 even more
Next, we lower the L0 of the SAE further, to 3. Results are shown below:
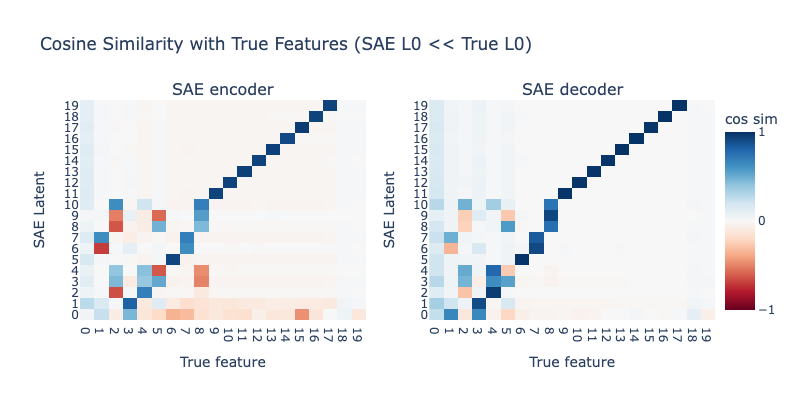
Lowering L0 further to 3 makes everything far worse. Although it's hard to tell from the plot, the magnitude of hedging (the extent to which is mixed into all other latents) is higher than with L0=4, and now all latents tracking higher-frequency features (features 1-10) are completely broken.
Case 3: SAE L0 > Toy Model L0
What happens if we set the SAE L0 too high? We now set the L0 of the SAE to 6. Results are shown below:
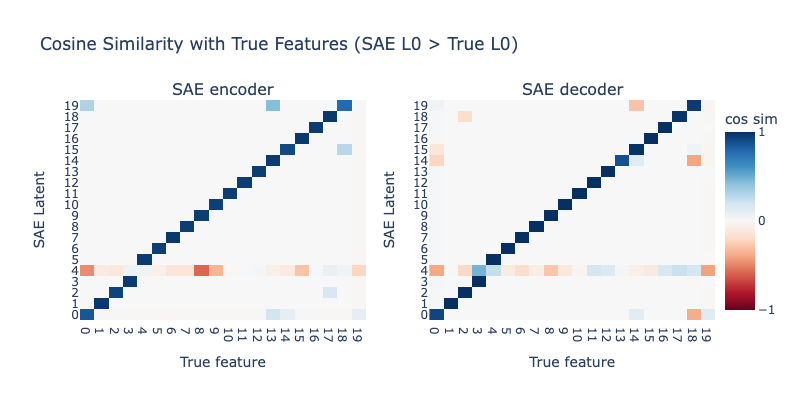
We see that the SAE learns some slightly broken latents, but there is no sign of systematic hedging. Instead, it seems like having too high of a L0 makes it so there are multiple ways to get perfect reconstruction loss, so we should not be surprised that the SAE settles into an imperfect result.
Increasing L0 even more
Next, we see what happens when we increase the SAE L0 even further. We set SAE L0 to 8. Results are shown below:
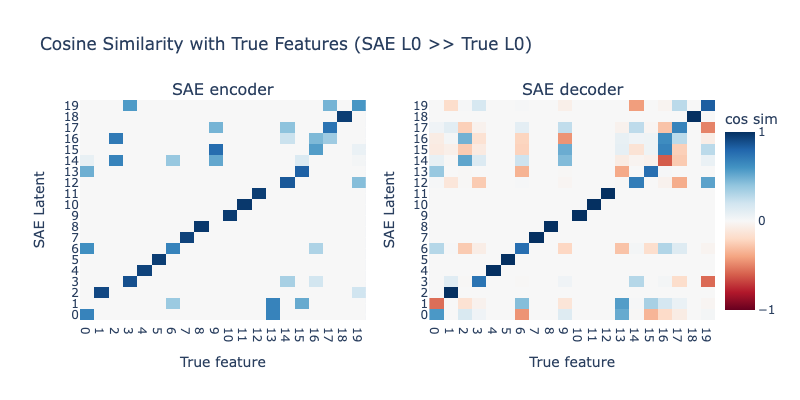
We now see the SAE is learning far worse latents than before, with most latents being completely broken. However, we still don't see any sign of systematic hedging like we saw with low L0 SAEs.
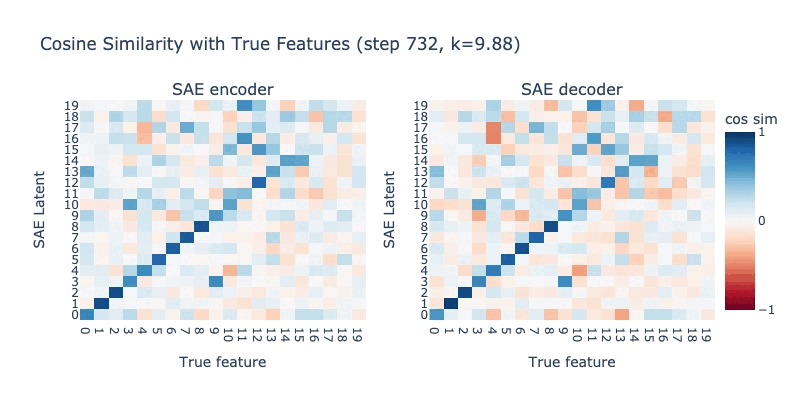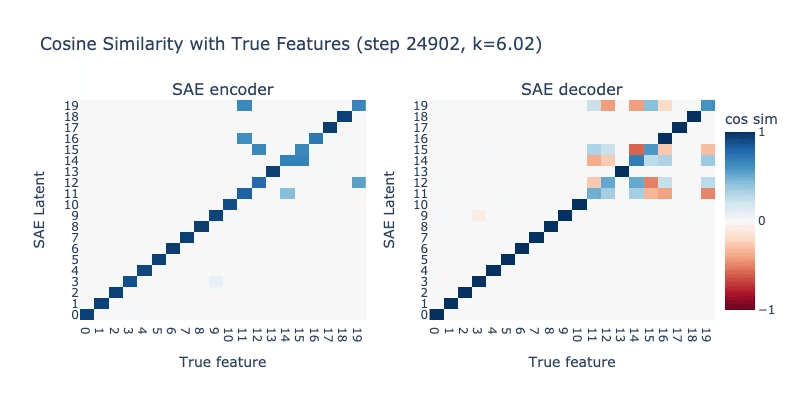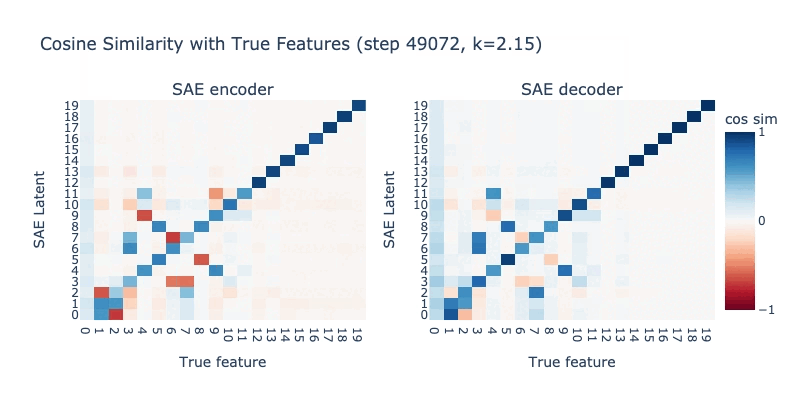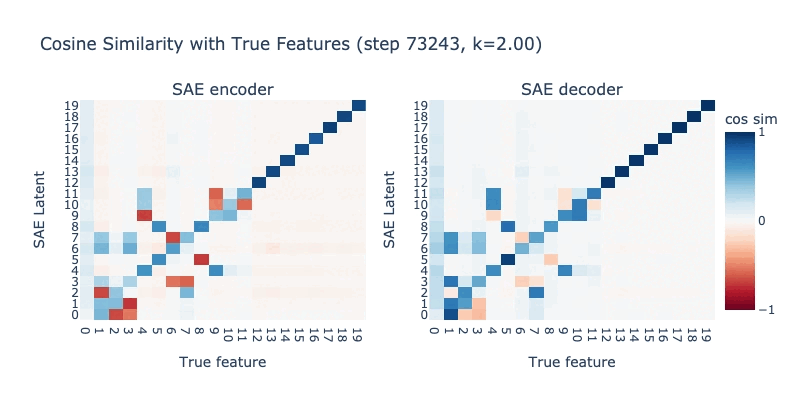
Watching an SAE break in real-time
Below, we record a training run where slowly decrease K from 10 to 2. The true L0 (and thus correct K) is 5 for this model. When K is too high, the SAE can find degenerate solutions, and low-frequency latents (latenst 10-19) are worse affected. When K=5, the SAE learns the true features perfectly. When K drops too low (below 5), we see feature hedging emerging, and the high-frequency latents (0-10) begin breaking.
Mixing high and low L0 penalties together
Clearly, if we knew the correct L0 of the underlying data, the best thing to do is to train at that L0. In reality, we do not yet have a way to find the true L0, but we find that we can still improve things by mixing together two MSE losses during training: One loss uses a low L0 and another uses a high L0.
This is conceptually similar to how Matryoshka SAEs[3] work. In a Matryoshka SAE, multiple losses are summed using different width prefixes. Here, we sum two losses using different L0s:
In this formualtion, is the MSE loss term using a lower L0, and is the MSE loss term using a higher L0. We add a coefficient so we can control the relative balance of these two losses.
Below, we train an SAE with , , :
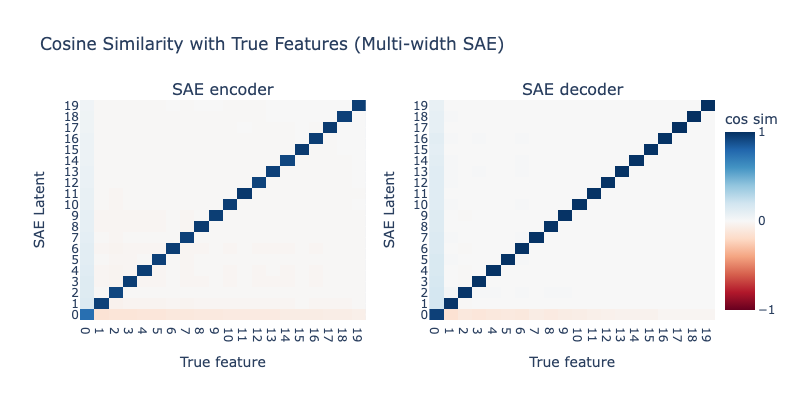
This looks a lot better than our Case 1 SAE - we still see a dedicated latent for , but there's also clear hedging going on still. Let's try increasing further to 20:
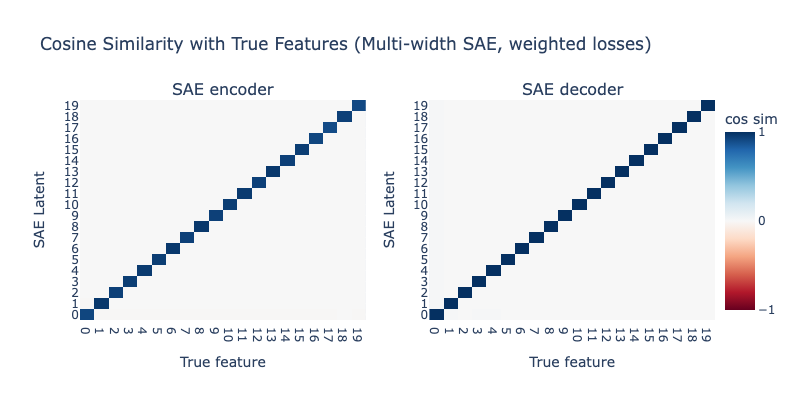
We've now perfectly recovered the true features again! It seems like the low-L0 loss helps keep the high-L0 loss from learning a degenerate solution, while the high-L0 loss keeps the low-L0 loss from engaging in hedging.
- ^
Kantamneni, Subhash, et al. "Are Sparse Autoencoders Useful? A Case Study in Sparse Probing." Forty-second International Conference on Machine Learning.
- ^
Bussmann, Bart, et al. "Learning Multi-Level Features with Matryoshka Sparse Autoencoders." Forty-second International Conference on Machine Learning.
- ^
Chanin, David, Tomáš Dulka, and Adrià Garriga-Alonso. "Feature Hedging: Correlated Features Break Narrow Sparse Autoencoders." arXiv preprint arXiv:2505.11756 (2025).
- ^
Chanin, David, et al. "A is for absorption: Studying feature splitting and absorption in sparse autoencoders." arXiv preprint arXiv:2409.14507 (2024).
- ^
Bussmann, Bart, Patrick Leask, and Neel Nanda. "BatchTopK Sparse Autoencoders." NeurIPS 2024 Workshop on Scientific Methods for Understanding Deep Learning.