Jacob Falcovich tells us that we should Kelly bet on everything. I discuss whether we should Kelly bet when we'd normally make small-money bets on disagreements. Lsusr reminds us that we aren't very good at intuitively grasping what the Kelly formula actually will say.
Due to Lsusr's post, I took another look at how I actually calculate Kelly. I'll describe the improved formulation I came up with. I'm curious to hear everyone else's thoughts on the quickest ways, or what formula you prefer, or how you intuitively estimate. If you already have opinions, take a moment to think what they are before reading further.
In the comments to my post on Kelly, Daniel Filan mentioned:
FWIW the version that I think I'll manage to remember is that the optional fraction of your bankroll to bet is the expected net winnings divided by the net winnings if you win.
I've found that I remember this formulation, but the difference between "net winnings" and "gross winnings" is enough to make me want to double-check things, and in the few months since writing the original post, I haven't actually used this to calculate Kelly.
"expected net winnings divided by net winnings if you win" is easy enough to remember, but is it easy enough to calculate? When I try to calculate it, I think of it this way:
[probability of success] [payoff of success] + [probability of failure] [payoff of failure] all divided by [payoff of success].
This is a combination of five numbers (one being a repeat). We have to calculate probability of failure from the probability of success (ie, 1-p). Then we perform two multiplications, one addition, and one division -- five steps of mental arithmetic.
But the formula is really a function of two numbers (see Lsusr's graph for a vivid illustration). Can we formulate the calculation in a way that feels like just a function of two numbers?
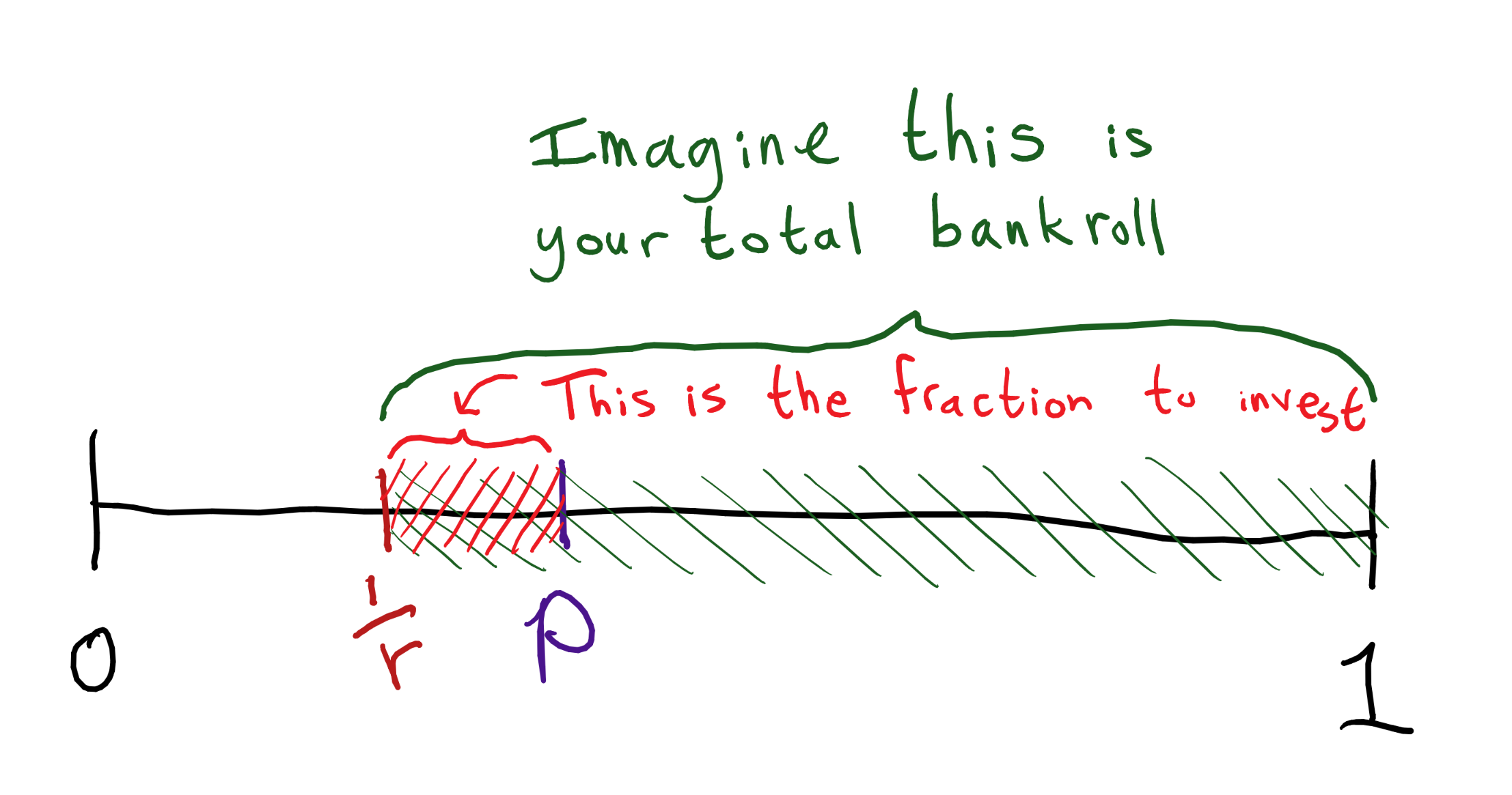
Normally the formula is stated in terms of , the net winnings if you win. I prefer to state it in terms of . If there's an opportunity to "double" your money, while ; so I think is more how people intuitively think about things.
In these terms, the break-even point is just . This is easy to reconstruct with mental checks: if you stand to double your money, you'd better believe your chances of winning are at least 50%; if you stand to quadruple your money, chances had better be at least 25%; and so on. If you're like me, calculating the break-even point as is much easier than "the point where net expected winnings equals zero" -- the expectation requires that I combine four numbers, while requires just one.
The Kelly formula is just a linear interpolation from 0% at the break-even point to 100% on sure things. (Again, see the graph.)
So one way to calculate Kelly is to ask how much along the way between and we are.
For example, if , then things start to be profitable after . If , we're 3/5ths of the way, so would invest that part of our bankroll.
If , then things start to be profitable after . If , then it's half way to , so we'd spend half of our bankroll.
If you're like me, this is much easier to calculate than "expected net winnings divided by the net winnings if you win". First I calculate . Then I just have to compare this to , to find where stands along the way from to 1. Technically, the formula for this is:
That's a combination of three numbers (counting the repeat), with four steps of mental arithmetic: finding , two subtractions, and one division. So that's a bit better. But, personally, I find that I don't really have to think in terms of the explicit formula for simple cases like the examples above. Instead, I imagine the number line from 0 to 1, and ask myself how far along is from to 1, and come up with answers.
This also seems like a better way to intuit approximate answers. If I think an event has a 15% chance, and the potential payoff of a bet is to multiply my investment by 30, then I can't immediately tell you what the Kelly bet is. However, I can immediately tell you that 15% is less than halfway along the distance from to 100%, and that it's more than a tenth of the way. So I know the Kelly bet isn't so much as half the bankroll, but it also isn't so little as 10%. (Erm, I got this example wrong on the first go and had to revise it when a commenter pointed out the mistake, so maybe actually check the math rather than just intuiting.)
Don't mix up and -- it's critical to remember which of these has to be higher, and not get them reversed. can be thought of as the house odds. You have an edge over the house if your estimate is higher; the house has an edge over you if its estimate is higher.
Keep in mind that the most you ever invest is p. For very small probabilities of very large payoffs, the percentage of your bankroll to invest remains small. You still want to check whether is more than . For example, a 1% chance of a 1000x payoff is good, because 1% is , which is more than . The amount you actually invest is a little less than : in our example, is almost th of the way from th to 1, so we know we'd invest about 1%. (The actual number is , so, a little more than .9%.)
So, what's your favorite version of the Kelly formula? Do you think you can beat mine in terms of ease of calculation?