Trying to understand John Wentworth's research agenda
44LawrenceC
3Algon
19Zvi
19Max H
17Zvi
12johnswentworth
9Emrik
1Emrik
8Domenic
7Bill Benzon
3Joseph Bloom
2mtaran
4habryka
New Comment
My hope is that products will give a more useful feedback signal than other peoples' commentary on our technical work.
I'm curious what form these "products" are intended to take -- if possible, could you give some examples of things you might do with a theory of natural abstractions? If I had to guess, the product will be an algorithm that identifies abstractions in a domain where good abstractions are useful, but I'm not sure how or in what domain.
Seconded. For personal reasons, I'd be interested if you can identify important concepts in a text document.
We can go look for such structures in e.g. nets, see how well they seem to match our own concepts, and have some reason to expect they'll match our own concepts robustly in certain cases.
Checking my own understanding with an example of what this might look like concretely:
Suppose you have a language model that can play Chess (via text notation). Presumably, the model has some kind of internal representation of the game, the board state, the pieces, and strategy. Those representations are probably complicated linear combinations / superpositions of activations and weights within the model somewhere. Call this representation in your notation.
If you just want a traditional computer program to play Chess you can use much simpler (or at least more bare metal / efficient) representations of the game, board state, and pieces as a 2-d array of integers or a bitmap or whatever, and write some relatively simple code to manipulate those data structures in ways that are valid according to the rules of Chess. Call this representation in your notation.
And, to the degree that the language model is actually capable of playing valid Chess (since that's when we would expect the preconditions to hold), you expect to be able to identify latents within the model and find a map from to , such that you can manipulate and use information you learn from those manipulations to precisely predict stuff about . More concretely, once you have the map, you can predict the moves of the language model by inspecting its internals and then translating them into the representation used by an ordinary Chess analysis program, and then, having predicted the moves, you'll be able to predict (and perhaps usefully manipulate) the language model's internal representations by mapping from back to .
And then the theorems are just saying under what conditions exactly you expect to be able to do this kind of thing, and it turns out those conditions are actually relatively lax.
Roughly accurate as an example / summary of the kind of thing you expect to be able to do?
After all the worries about people publishing things they shouldn't, I found it very surprising to see Oliver advocating for publishing when John wanted to hold back, combined with the request for incremental explanations of progress to justify continued funding.
John seems to have set a very high alternative proof bar here - do things other people can't do. That seems... certainly good enough, if anything too stringent? We need to find ways to allow deep, private work.
To be clear, the discussion about feedback loops was mostly about feedback loops for me (and David), i.e. outside signals for us to make sure we haven't lost contact with reality. This was a discussion about epistemics, not a negotiation over preconditions of funding.
It seems generally quite bad for somebody like John to have to justify his research in order to have an income. A mind like this is better spent purely optimizing for exactly what he thinks is best, imo.
When he knows that he must justify himself to others (who may or may not understand his reasoning), his brain's background-search is biased in favour of what-can-be-explained. For early thinkers, this bias tends to be good, because it prevents them from bullshitting themselves. But there comes a point where you've mostly learned not to bullshit yourself, and you're better off purely aiming your cognition based on what you yourself think you understand.
Vingean deference-limits + anti-inductive innovation-frontier
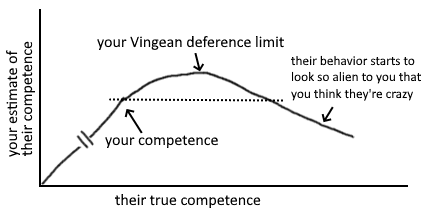
Paying people for what they do works great if most of their potential impact comes from activities you can verify. But if their most effective activities are things they have a hard time explaining to others (yet have intrinsic motivation to do), you could miss out on a lot of impact by requiring them instead to work on what's verifiable.
The people who are much higher competence will behave in ways you don't recognise as more competent. If you were able to tell what right things to do are, you would just do those things and be at their level. Your "deference limit" is the level of competence above your own at which you stop being able to reliable judge the difference.
Innovation on the frontier is anti-inductive. If you select people cautiously, you miss out on hiring people significantly more competent than you.[1]
Costs of compromise
Consider how the cost of compromising between optimisation criteria interacts with what part of the impact distribution you're aiming for. If you're searching for a project with top p% impact and top p% explainability-to-funders, you can expect only p^2 of projects to fit both criteria—assuming independence.
But I think it's an open question how & when the distributions correlate. One reason to think they could sometimes be anticorrelated [sic] is that the projects with the highest explainability-to-funders are also more likely to receive adequate attention from profit-incentives alone.[2]
Consider funding people you are strictly confused by wrt what they prioritize
If someone believes something wild, and your response is strict confusion, that's high value of information. You can only safely say they're low-epistemic-value if you have evidence for some alternative story that explains why they believe what they believe.
Alternatively, find something that is surprisingly popular—because if you don't understand why someone believes something, you cannot exclude that they believe it for good reasons.[3]
The crucial freedom to say "oops!" frequently and immediately
Still, I really hope funders would consider funding the person instead of the project, since I think Johannes' potential will be severely stifled unless he has the opportunity to go "oops! I guess I ought to be doing something else instead" as soon as he discovers some intractable bottleneck wrt his current project. (...) it would be a real shame if funding gave him an incentive to not notice reasons to pivot.[4]
- ^
Comment explaining why I think it would be good if exceptional researchers had basic income (evaluate candidates by their meta-level process rather than their object-level beliefs)
- ^
Comment explaining what costs of compromise in conjunctive search implies for when you're "sampling for outliers"
- ^
Comment explaining my approach to finding usefwl information in general
- ^
re the Vingean deference-limit thing above:
It quite aptly analogizes to the Nyquist frequency , which is the highest [max frequency component] a signal can have before you lose the ability to uniquely infer its components from a given sample rate .
Also, I'm renaming it "Vingean disambiguation-limit".[1]
P.S. , which means that you can only disambiguate signals whose max components are below half your sample rate. Above that point, and you start having ambiguities (aliases).
- ^
The "disambiguation limit" class has two members now. The inverse is the "disambiguation threshold", which is the measure of power you require of your sampler/measuring-device in order to disambiguate between things-measured above a given measure.
...stating things as generally as feasible helps wrt finding metaphors. Hence the word-salad above. ^^'
I've had a hard time connecting John's work to anything real. It's all over Bayes nets, with some (apparently obviously true https://www.lesswrong.com/posts/2WuSZo7esdobiW2mr/the-lightcone-theorem-a-better-foundation-for-natural?commentId=K5gPNyavBgpGNv4m3 ) theorems coming out of it.
In contrast, look at work like Anthropic's superposition solution, or the representation engineering paper from CAIS. If someone told me "I'm interested in identifying the natural abstractions AIs use when producing their output", that is the kind of work I'd expect. It's on actual LLMs! (Or at least "LMs", for the Anthropic paper.) They identified useful concepts like "truth-telling" or "Arabic"!
In John's work, his prose often promises he'll point to useful concepts like different physics models, but the results instead seem to operate on the level of random variables and causal diagrams. I'd love to see any sign this work is applicable toward real-world AI systems, and can, e.g., accurately identify what abstractions GPT-2 or LLaMA are using.
"...to understand the conditions under which AI will develop the same abstractions as humans do..."
I know from observation that ChatGPT has some knowledge of the concepts of justice and charity. It can define them in a reasonable way and create stories illustrating them. In some sense, it understands those concepts, and it arrived at them, I presume, through standard pretraining. Has it therefore developed those abstractions in the sense you're talking about?
I'd be very interested in seeing these products and hearing about the use-cases / applications. Specifically, my prior experience at a startup leads me to believe that building products while doing science can be quite difficult (although there are ways that the two can synergise).
I'd be more optimistic about someone claiming they'll do this well if there is an individual involved in the project who is both deeply familiar with the science and has build products before (as opposed to two people each counting on the other to have sufficient expertise they lack).
A separate question I have is about how building products might be consistent with being careful about what information you make public. If you there are things that you don't want to be public knowledge, will there be proprietary knowledge not shared with users/clients? It seems like a non-trivial problem to maximize trust/interest/buy-in whilst minimizing clues to underlying valuable insights.
It'd be great if one of the features of these "conversation" type posts was that they would get an LLM-genererated summary or a version of it not as a conversation. Because at least for me this format is super frustrating to read and ends up having a lower signal to noise ratio.
I do think at least for a post like this, the likelihood the LLM would get any of the math right is pretty low. I do think some summary that allows people to decide whether to read the thing is pretty valuable, but I think it's currently out of reach to have a summary actually contain the relevant ideas/insights in a post.
Curated and popular this week