The Workshop

Late in July I organized and held MIRIx Tel-Aviv with the goal of investigating the currently-open (to my knowledge) Friendly AI problem called "logical probability": the issue of assigning probabilities to formulas in a first-order proof system, in order to use the reflective consistency of the probability predicate to get past the Loebian Obstacle to building a self-modifying reasoning agent that will trust itself and its successors. Vadim Kosoy, Benjamin and Joshua Fox, and myself met at the Tel-Aviv Makers' Insurgence for six hours, and each presented our ideas. I spent most of it sneezing due to my allergies to TAMI's resident cats.

My idea was to go with the proof-theoretic semantics of logic and attack computational construction of logical probability via the Curry-Howard Isomorphism between programs and proofs: this yields a rather direct translation between computational constructions of logical probability and the learning/construction of an optimal function from sensory inputs to actions required by Updateless Decision Theory.

The best I can give as a mathematical result is as follows:

$P(\Gamma \vdash a:A \mid \Gamma \vdash b:B) = P(\Gamma,x:B \vdash [\forall y:B, x/y]a:A)$

$P(\Gamma \vdash (a, b): A \wedge B) = P(\Gamma \vdash a:A \mid \Gamma \vdash b:B) * P(\Gamma \vdash b:B)$

$\frac{x:A \notin \Gamma}{P(\Gamma \vdash x:A) = \mathcal{M}_{\lambda\mu} (A)}$

$\frac{x:A \in \Gamma}{P(\Gamma \vdash x:A) = 1.0}$

The capital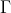 $\Gamma$ is a set of hypotheses/axioms/assumptions, and the English letters are metasyntactic variables (like "foo" and "bar" in programming lessons). The lower-case letters denote proofs/programs, and the upper-case letters denote propositions/types. The turnstile 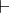$\vdash$ just means "deduces": the judgement 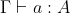$\Gamma \vdash a:A$ can be read here as "an agent whose set of beliefs is denoted 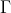$\Gamma$ will believe that the evidence a proves the proposition A." The $[\forall y:B, x/y]a$ performs a "reversed" substitution, with the result reading: "for all y proving/of-type B, substitute x for y in a". 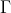This means that we algorithmically build a new proof/construction/program from a in which any and all constructions proving the proposition B are replaced with the logically-equivalent hypothesis x, which we have added to our hypothesis-set $\Gamma$ .

Thus the first equation reads, "the probability of a proving A conditioned on b proving B equals the probability of a proving A when we assume the truth of B as a hypothesis." The second equation then uses this definition of conditional probability to give the normal Product Rule of probabilities for the logical product (the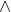 $\wedge$ operator), defined proof-theoretically. I strongly believe I could give a similar equation for the normal Sum Rule of probabilities for the logical sum (the 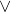$\vee$ operator) if I could only access the relevant paywalled paper, in which the λμ-calculus acting as an algorithmic interpretation of the natural-deduction system for classical propositional logic (rather than intuitionistic) is given.

The third item given there is an inference rule, which reads, "if x is a free variable/hypothesis imputed to have type/prove proposition A, not bound in the hypothesis-set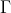 $\Gamma$ , then the probability with which we believe x proves A is given by the Solomonoff Measure of type A in the λμ-calculus". We can define that measure simply as the summed Solomonoff Measure of every program/proof possessing the relevant type, and I don't think going into the details of its construction here would be particularly productive. Free variables in λ-calculus are isomorphic to unproven hypotheses in natural deduction, and so a probabilistic proof system could learn how much to believe in some free-standing hypothesis via Bayesian evidence rather than algorithmic proof.

The final item given here is trivial: anything assumed has probability 1.0, that of a logical tautology.

The upside to invoking the strange, alien λμ-calculus instead of the more normal, friendly λ-calculus is that we thus reason inside classical logic rather than intuitionistic, which means we can use the classical axioms of probability rather than intuitionistic Bayesianism. We need classical logic here: if we switch to intuitionistic logics (Heyting algebras rather than Boolean algebras) we do get to make computational decidability a first-class citizen of our logic, but the cost is that we can then believe only computationally provable propositions. As Benjamin Fox pointed out to me at the workshop, Loeb's Theorem then becomes a triviality, with real self-trust rendered no easier.

The Apologia

My motivation and core idea for all this was very simple: I am a devout computational trinitarian, believing that logic must be set on foundations which describe reasoning, truth, and evidence in a non-mystical, non-Platonic way. The study of first-order logic and especially of incompleteness results in metamathematics, from Goedel on up to Chaitin, aggravates me in its relentless Platonism, and especially in the way Platonic mysticism about logical incompleteness so often leads to the belief that minds are mystical. (It aggravates other people, too!)

The slight problem which I ran into is that there's a shit-ton I don't know about logic. I am now working to remedy this grievous hole in my previous education. Also, this problem is really deep, actually.

I thus apologize for ending the rigorous portion of this write-up here. Everyone expecting proper rigor, you may now pack up and go home, if you were ever paying attention at all. Ritual seppuku will duly be committed, followed by hors d'oeuvre. My corpse will be duly recycled to make paper-clips, in the proper fashion of a failed LessWrongian.

The Parts I'm Not Very Sure About

With any luck, that previous paragraph got rid of all the serious people.

I do, however, still think that the (beautiful) equivalence between computation and logic can yield some insights here. After all, the whole reason for the strange incompleteness results in first-order logic (shown by Boolos in his textbook, I'm told) is that first-order logic, as a reasoning system, contains sufficient computational machinery to encode a Universal Turing Machine. The bidirectionality of this reduction (Hilbert and Gentzen both have given computational descriptions of first-order proof systems) is just another demonstration of the equivalence.

In fact, it seems to me (right now) to yield a rather intuitively satisfying explanation of why the Gaifman-Carnot Condition (that every instance we see of $P(x_i)$ provides Bayesian evidence in favor of $\forall x.P(x)$ ) for logical probabilities is not computably approximable. What would we need to interpret the Gaifman Condition from an algorithmic, type-theoretic viewpoint? From this interpretation, we would need a proof of our universal generalization. 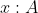This would have to be a dependent product of form $\Pi(x:A).P(x)$ , a function taking any construction $x:A$ to a construction of type $P(x)$ , which itself has type Prop. To learn such a dependent function from the examples would be to search for an optimal (simple, probable) construction (program) constituting the relevant proof object: effectively, an individual act of Solomonoff Induction. Solomonoff Induction, however, is already only semicomputable, which would then make a Gaifman-Hutter distribution (is there another term for these?) doubly semicomputable, since even generating it involves a semiprocedure.

The benefit of using the constructive approach to probabilistic logic here is that we know perfectly well that however incomputable Solomonoff Induction and Gaifman-Hutter distributions might be, both existing humans and existing proof systems succeed in building proof-constructions for quantified sentences all the time, even in higher-order logics such as Coquand's Calculus of Constructions (the core of a popular constructive proof assistant) or Luo's Logic-Enriched Type Theory (the core of a popular dependently-typed programming language and proof engine based on classical logic). Such logics and their proof-checking algorithms constitute, going all the way back to Automath, the first examples of computational "agents" which acquire specific "beliefs" in a mathematically rigorous way, subject to human-proved theorems of soundness, consistency, and programming-language-theoretic completeness (rather than meaning that every true proposition has a proof, this means that every program which does not become operationally stuck has a type and is thus the proof of some proposition). If we want our AIs to believe in accordance with soundness and consistency properties we can prove before running them, while being composed of computational artifacts, I personally consider this the foundation from which to build.

Where we can acquire probabilistic evidence in a sound and computable way, as noted above in the section on free variables/hypotheses, we can do so for propositions which we cannot algorithmically prove. This would bring us closer to our actual goals of using logical probability in Updateless Decision Theory or of getting around the Loebian Obstacle.

Some of the Background Material I'm Reading

Another reason why we should use a Curry-Howard approach to logical probability is one of the simplest possible reasons: the burgeoning field of probabilistic programming is already being built on it. The Computational Cognitive Science lab at MIT is publishing papers showing that their languages are universal for computable and semicomputable probability distributions, and getting strong results in the study of human general intelligence. Specifically: they are hypothesizing that we can dissolve "learning" into "inducing probabilistic programs via hierarchical Bayesian inference", "thinking" into "simulation" into "conditional sampling from probabilistic programs", and "uncertain inference" into "approximate inference over the distributions represented by probabilistic programs, conditioned on some fixed quantity of sampling that has been done."

In fact, one might even look at these ideas and think that, perhaps, an agent which could find some way to sample quickly and more accurately, or to learn probabilistic programs more efficiently (in terms of training data), than was built into its original "belief engine" could then rewrite its belief engine to use these new algorithms to perform strictly better inference and learning. Unless I'm as completely wrong as I usually am about these things (that is, very extremely completely wrong based on an utterly unfounded misunderstanding of the whole topic), it's a potential engine for recursive self-improvement.

They also have been studying how to implement statistical inference techniques for their generate modeling languages which do not obey Bayesian soundness. While most of machine learning/perception works according to error-rate minimization rather than Bayesian soundness (exactly because Bayesian methods are often too computationally expensive for real-world use), I would prefer someone at least study the implications of employing unsound inference techniques for more general AI and cognitive-science applications in terms of how often such a system would "misbehave".

Many of MIT's models are currently dynamically typed and appear to leave type soundness (the logical rigor with which agents come to believe things by deduction) to future research. And yet: they got to this problem first, so to speak. We really ought to be collaborating with them, with the full-time grant-funded academic researchers, rather than trying to armchair-reason our way to a full theory of logical probability as a large group of amateurs or part-timers and only a small core cohort of full-time MIRI and FHI staff investigating AI safety issues.

(I admit to having a nerd crush, and I am actually planning to go visit the Cocosci Lab this coming week, and want/intend to apply to their PhD program.)

They have also uncovered something else I find highly interesting: human learning of both concepts and causal frameworks seems to take place via hierarchical Bayesian inference, gaining a "blessing of abstraction" to countermand the "curse of dimensionality". The natural interpretation of these abstractions in terms of constructions and types would be that, as in dependently-typed programming languages, constructions have types, and types are constructions, but for hierarchical-learning purposes, it would be useful to suppose that types have specific, structured types more informative than Prop or Type_n (for some universe level n). Inference can then proceed from giving constructions or type-judgements as evidence at the bottom level, up the hierarchy of types and meta-types to give probabilistic belief-assignments to very general knowledge. Even very different objects could have similar meta-types at some level of the hierarchy, allowing hierarchical inference to help transfer Bayesian evidence between seemingly different domains, giving insight into how efficient general intelligence can work.

Just-for-fun Postscript

If we really buy into the model of thinking as conditional simulation, we can use that to dissolve the modalities "possible" and "impossible". We arrive at (by my count) three different ways of considering the issue computationally:

Conceivable/imaginable: the generative models which constitute my current beliefs do or do not yield a path to make some logical proposition true or to make some causal event happen (planning can be done as inference, after all), with or without some specified level of probability.
Sensibility/absurdity: the generative models which constitute my current beliefs place a desirably high or undesirably low probability on the known path(s) by which a proposition might be true or by which an event might happen. The level which constitutes "desirable" could be set as the $\alpha$ value for a hypothesis test, or some other value determined decision-theoretically. This could relate to Pascal's Mugging: how probable must something be before I consider it real rather than an artifact of my own hypothesis space?
Consistency or Contradiction: the generative models which constitute my current beliefs, plus the hypothesis that some proposition is true or some event can come about, do or do not yield a logical contradiction with some probability (that is, we should believe the contradiction exists only to the degree we believe in our existing models in the first place!).

I mostly find this fun because it lets us talk rigorously about when we should "shut up and do the 1,2!impossible" and when something is very definitely 3!impossible.