There's a standard explanation in game theory as to why wars or fought (or lawsuits are brought to trial, etc.), even when everyone would be better off with a negotiated settlement that avoids expensive conflict. Even assuming that it's possible to enforce an agreement, there's still a problem. In order to induce militarily strong parties (in terms of capability or willingness to fight) to accept the agreement rather than fight, the agreement must be appropriately tilted in their favor. If there is asymmetric information about the relative military strength of the parties, then in equilibrium, wars must be fought with positive probability.
Perhaps not standard. But another possible explanation of why wars are fought is that any specific war might be a sub-optimal move, but that making a plausible pre-commitment to a war as a general policy is a good disincentive for other people to avoid conflicts with you. You asked for some territory from me, we could negotiate a mutually acceptable compromise, but then maybe all those other jerks also start asking me for land. Maybe I value that disincentive highly.
Another factor is that all the farmers and mooks who will loose limbs and lives are not invited to the decision-making table. This maybe moves the goalposts, as we don't do game-theory for the countries, but for their leaders/negotiators. eg. "This war will make me a national hero. Plus this is good for our country as it exists as a concept, in that it gets physically bigger and more complete. My own place in history and the integrity of my country's identity are each worth roughly one of my own limbs to me. Fortunately I will only have to pay with other people's, so by my utility function this war is a steal!"
Isn't there an equilibrium where people assume other people's militaries are as strong as they can demonstrate, and people just fully disclose their military strength?
Sort of! This paper (of which I’m a coauthor) discusses this “unraveling” argument, and the technical conditions under which it does and doesn’t go through. Briefly:
- It’s not clear how easy it is to demonstrate military strength in the context of an advanced AI civilization, in a way that can be verified / can’t be bluffed. If I see that you’ve demonstrated high strength in some small war game, but my prior on you being that strong is sufficiently low, I’ll probably think you’re bluffing and wouldn’t be that strong in the real large-scale conflict.
- Supposing strength can be verified, it might be intractable to do so without also disclosing vulnerable info (irrelevant to the potential conflict). As TLW's comment notes, the disclosure process itself might be really computationally expensive.
- But if we can verifiably disclose, and I can either selectively disclose only the war-relevant info or I don’t have such a vulnerability, then yes you’re right, war can be avoided. (At least in this toy model where there’s a scalar “strength” variable; things can get more complicated in multiple dimensions, or where there isn’t an “ordering” to the war-relevant info.)
- Another option (which the paper presents) is conditional disclosure—even if you could exploit me by knowing the vulnerable info, I commit to share my code if and only if you commit to share yours, play the cooperative equilibrium, and not exploit me.
As TLW's comment notes, the disclosure process itself might be really computationally expensive.
I was actually thinking of the cost of physical demonstrations, and/or the cost of convincing others that simulations are accurate[1], not so much direct simulation costs.
That being said, this is still a valid point, just not one that I should be credited for.
- ^
Imagine trying to convince someone of atomic weapons purely with simulations, without anyone ever having detonated one[2], for instance. It may be doable; it'd be nowhere near cheap.
Now imagine trying to do so without allowing the other side to figure out how to make atomic bombs in the process...
- ^
To be clear: as in alt-history-style 'Trinity / etc never happened'. Not just as in someone today convincing another that their particular atomic weapon works.
Demonstrating military strength is itself often a significant cost.
Say your opponent has a military of strength 1.1x, and is demonstrating it.
If you have the choice of keeping and demonstrating a military of strength x, or keeping a military of strength 1.2 and not demonstrating at all...
As an example, part of your military strength might be your ability to crash enemy systems with zero-day software exploits (or any other kind of secret weapon they don't yet have counters for). At least naively, you can't demonstrate you have such a weapon without rendering it useless. Though this does suggest a (unrealistically) high-coordination solution to at least this version of the problem: have both sides declare all their capabilities to a trusted third party who then figures out the likely costs and chances of winning for each side.
Though this does suggest a (unrealistically) high-coordination solution to at least this version of the problem: have both sides declare all their capabilities to a trusted third party who then figures out the likely costs and chances of winning for each side.
Is that enough?
Say Alice thinks her army is overwhelmingly stronger than Bob. (In fact Bob has a one-time exploit that allows Bob to have a decent chance to win.) The third party says that Bob has a 50% chance of winning. Alice can then update P(exploit), and go 'uhoh' and go back and scrub for exploits.
(So... the third-party scheme might still work, but only once I think.)
Good point, so continuing with the superhuman levels of coordination and simulation: instead of Alice and Bob saying "we're thinking of having a war" and Simon saying "if you did, Bob would win with probability p"; Alice and Bob say "we've committed to simulating this war and have pre-signed treaties based on various outcomes", and then Simon says "Bob wins with probability p by deploying secret weapon X, so Alice you have to pay up according to that if-you-lose treaty". So Alice does learn about the weapon but also has to pay the price for losing, exactly like she would in an actual war (except without the associated real-world damage).
Interesting!
How does said binding treaty come about? I don't see any reason for Alice to accept such a treaty in the first place.
Alice would instead propose (or counter-propose) a treaty that always takes the terms that would result from the simulation according to Alice's estimate.
Alice is always at least indifferent to this, and the only case where Bob is not at least indifferent to this is if Bob is stronger than Alice's estimate, in which case accepting said treaty would not be in Alice's best interest. (Alice should instead stall and hunt for exploits, give or take.)
Simon's services are only offered to those who submit a treaty over a full range of possible outcomes. Alice could try to bully Bob into accepting a bullshit treaty ("if I win you give me X; if I lose you still give me X"), but just like today Bob has the backup plan of refusing arbitration and actually waging war. (Refusing arbitration is allowed; it's only going to arbitration and then not abiding by the result that is verboten.) And Alice could avoid committing to concessions-on-loss by herself refusing arbitration and waging war, but she wouldn't actually be in a better position by doing so, since the real-world war also involves her paying a price in the (to her mind) unlikely event that Bob wins and can extract one. Basically the whole point is that, as long as the simulated war and the agreed-upon consequences of war (minus actual deaths and other stuff) match a potential real-world war closely enough, then accepting the simulation should be a strict improvement for both sides regardless of their power differential and regardless of the end result, so both sides should (bindingly) accept.
Here's an example game tree:
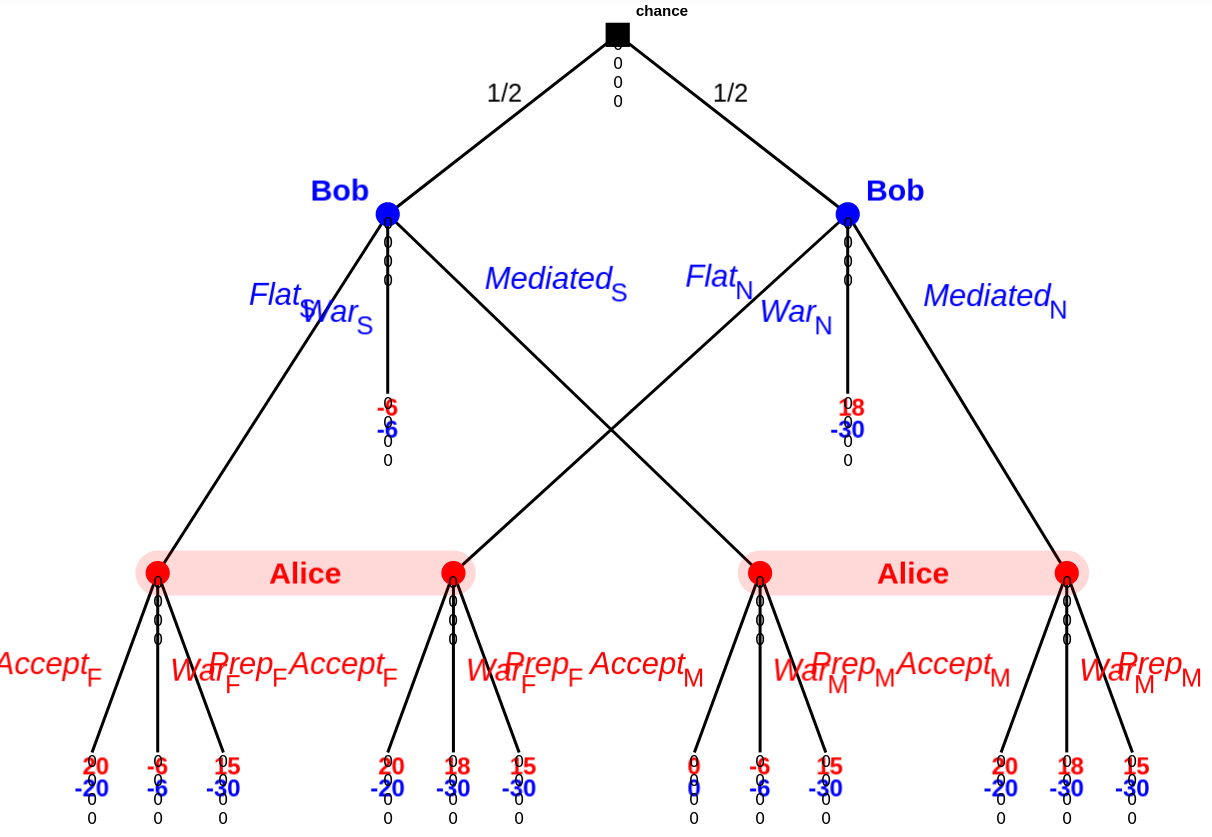
(Kindly ignore the zeros below each game node; I'm using the dev version of GTE, which has a few quirks.)
Roughly speaking:
- Bob either has something up his sleeve (an exploit of some sort), or does not.
- Bob either:
- Offers a flat agreement (well, really surrender) to Alice.
- Offers a (binding once both sides agree to it) arbitrated (mediated in the above; I am not going to bother redoing the screenshot above) agreement by a third party (Simon) to Alice.
- Goes directly to war with Alice.
- Assuming Bob didn't go directly to war, Alice either:
Wars cost the winner 2 and the loser 10, and also transfers 20 from the loser to the winner. (So normally war is normally +18 / -30 for the winner/loser.).
Alice doing an audit/preparing costs 3, on top of the usual, regardless of if there's actually an exploit.
Alice wins all the time unless Bob has something up his sleeve and Alice doesn't prepare. (+18/-30, or +15/-30 if Alice prepared.) Even in that case, Alice wins 50% of the time. (-6 / -6). Bob has something up his sleeve 50% of the time.
Flat offer here means 'do the transfer as though there was a war, but don't destroy anything'. A flat offer is then always +20 for Alice and -20 for Bob.
Arbitrated means 'do a transfer based on the third party's evaluation of the probability of Bob winning, but don't actually destroy anything'. So if Bob has something up his sleeve, Charlie comes back with a coin flip and the result is 0, otherwise it's +20/-20.
There are some 17 different Nash equilibria here, with an EP from +6 to +8 for Alice and -18 to -13 for Bob. As this is a lot, I'm not going to list them all. I'll summarize:
- There are 4 different equilibria with Bob always going to war immediately. Payoff in all of these cases is +6 / -18.
- There are 10 different equilibria with Bob always trying an arbitrated agreement if Bob has nothing up his sleeve, and going to war 2/3rds of the time if Bob has something up his sleeve (otherwise trying a mediated agreement in the other 1/3rd), with various mixed strategies in response. All of these cases are +8 / -14.
- There are 3 different equilibria with Bob always going to war if Bob has something up his sleeve, and always trying a flat agreement otherwise, with Alice always accepting a flat agreement and doing various strategies otherwise. All of these cases are +7 / -13.
Notably, Alice and Bob always offering/accepting an arbitrated agreement is not an equilibrium of this game[3]. None of these equilibria result in Alice and Bob always doing arbitration. (Also notably: all of these equilibria have the two sides going to war at least occasionally.)
There are likely other cases with different payoffs that have an equilibrium of arbitration/accepting arbitration; this example suffices to show that not all such games lead to said result as an equilibrium.
- ^
I use 'audit' in most of this; I used 'prep' for the game tree because otherwise two options started with A.
- ^
read: go 'uhoh' and spend a bunch of effort finding/fixing Bob's presumed exploit.
- ^
This is because, roughly, a Nash equilibrium requires that both sides choose a strategy that is best for them given the other party's response, but if Bob chooses MediatedS / MediatedN, then Alice is better off with PrepM over AcceptM. Average payout of 15 instead of 10. Hence, this is not an equilibrium.
I guess the obvious question is how dath ilan avoids this with better equilibria-- perhaps every party has spies to prevent asymmetric information, and preventing spies is either impossible or an escalatory action met with retaliation?
I bet when dath ilan kicks off their singularity, they end up implementing their CEV in such a way as to not create an incentive for any one group to race to the end, to be sure my values aren't squelched if someone else gets there first. That whole final fight over the future can be avoided, since the overall value-pie is about to grow enormously! Everyone can have more of what they want in the end, if we're smart enough to think through our binding contracts now.
How does one go about constructing a binding contract on the threshold of singularity? What enforcement mechanism would survive the transition?
When Dath Ilan kicks off their singularity, all the Illuminati factions (keepers, prediction market engineers, secret philosopher kings) who actually run things behind the scenes will murder each other in an orgy of violence, fracturing into tiny subgroups as each of them tries to optimize control over the superintelligence. To do otherwise would be foolish. Binding arbitration cannot hold across a sufficient power/intelligence/resource gap unless submitting to binding arbitration is part of that party's terminal values.
In one of the dath ilan stories, they did start the process of engaging in hostile actions in some other civilization's territory within minutes of first contact. The "smartest people in Civilization" acted very stupidly in that one, though I suppose it was because Eliezer didn't get to write both sides of the conflict.
Epistemic status: Rambly; probably unimportant; just getting an idea that's stuck with me out there. Small dath-ilan-verse spoilers throughout, as well as spoilers for Sid Meier's Alpha Centauri (1999), in case you're meaning to get around to that.
The idea that's most struck me reading Yudkowsky et al.'s dath ilani fiction is the idea that dath ilan is puzzled by war. Theirs isn't a moral puzzlement; they're puzzled at how ostensibly intelligent actors could fail to notice that everyone can do strictly better if they could just avoid fighting and instead sign enforceable treaties to divide the resources that would have been spent or destroyed fighting.
This … isn't usually something that figures into our vision for the science-fiction future. Take Sid Meier's Alpha Centauri (SMAC), a game whose universe absolutely fires my imagination. It's a 4X title, meaning that it's mostly about waging and winning ideological space war on the hardscrabble space frontier. As the human factions on Planet's surface acquire ever more transformative technology ever faster, utterly transforming that world in just a couple hundred years as their Singularity dawns … they put all that technology to use blowing each other to shreds. And this is totally par for the course for hard sci-fi and the human future of the vision generally. War is a central piece of the human condition; always has been. We don't really picture that changing as we get modestly superintelligent AI. Millenarian ideologies that preach the end of war … so preach because of how things will be once they have completely won the final war, not because of game theory that could reach across rival ideologies. The idea that intelligent actors who fundamentally disagree with one another's moral outlooks will predictably stop fighting at a certain intelligence threshold not all that far above IQ 100, because fighting isn't Pareto optimal … totally blindsides my stereotype of the science-fiction future. The future can be totally free of war, not because any single team has taken over the world, but because we got a little smarter about bargaining.
Let's jump back to SMAC:
This is the game text that appears as the human factions on Planet approach their singularity. Because the first faction to kick off their singularity will have an outsized influence on the utility function inherited by their superintelligence, late-game war with horrifyingly powerful weapons is waged to prevent others from beating your faction to the singularity. The opportunity to make everything way better … creates a destructive race to that opportunity, waged with antimatter bombs and more exotic horrors.
I bet when dath ilan kicks off their singularity, they end up implementing their CEV in such a way as to not create an incentive for any one group to race to the end, to be sure my values aren't squelched if someone else gets there first. That whole final fight over the future can be avoided, since the overall value-pie is about to grow enormously! Everyone can have more of what they want in the end, if we're smart enough to think through our binding contracts now.
Moral of the story: beware of pattern matching the future you're hoping for to either more of the past or to familiar fictional examples. Smart, more agentic actors behave differently.