8 Answers sorted by
1510
I think the answer pretty much has to be "yes", for the following reasons.
- As noted in the above post, weather is chaotic.
- Elections are sometimes close. For example, the winner of the 2000 presidential election came down to a margin of 537 votes in Florida.
- Geographic location correlates reasonably strongly with party preference.
- Weather affects specific geographic areas.
- Weather influences voter turnout[1] --
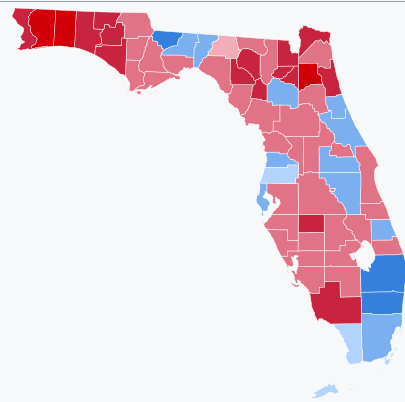
During the 2000 election, in Okaloosa County, Florida (at the western tip of the panhandle), 71k of the county's 171k residents voted, with 52186 votes going to Bush and 16989 votes going to Gore, for a 42% turnout rate.
On the day of November 7, 2000, there was no significant rainfall in Pensacola (which is the closest weather station I could find with records going back that far). A storm which dropped 2 inches of rain on the tip of the Florida panhandle that day would have reduced voter turnout by 1.8%,[1] which would have resulted in a margin that leaned 634 votes closer to Gore. Which would have tipped Florida, which would in turn have tipped the election.
Now, November is the "dry" season in Florida, so heavy rains like that are not incredibly common. Still, they can happen. For example, on 2015-11-02, 2.34 inches of rain fell.[2] That was only one day, out of the 140 days I looked at, which would have flipped the 2000 election, and the 2000 election was, to my knowledge, the closest of the 59 US presidential elections so far. Still, there are a number of other tracks that a storm could have taken, which would also have flipped the 2000 election.[3] And in the 1976 election, somewhat worse weather in the great lakes region would likely have flipped Ohio and Wisconsin, where Carter beat Ford by narrow margins.[4]
So I think "weather, on election day specifically, flips the 2028 election in a way that cannot be foreseen now" is already well over 0.1%. And that's not even getting into other weather stuff like "how many hurricanes hit the gulf coast in 2028, and where exactly do they land?".
- ^
"The results indicate that if a county experiences an inch of rain more than what is normal for the county for that election date, the percentage of the voting age population that turns out to vote decreases by approximately .9%.".
- ^
I pulled the weather for the week before and after November 7 for the past 10 years from the weather.gov api and that was the highest rainfall date.
var precipByDate = {} for (var y = 2014; y < 2024; y++) { var res = await fetch('https://api.weather.com/v1/location/KPNS:9:US/observations/historical.json?apiKey=<redacted>&units=e&startDate='+y+'1101&endDate='+y+'1114').then(r => r.json()); res.observations.forEach(obs => { var d = new Date(obs.valid_time_gmt*1000); var ds = d.getFullYear()+'-'+(d.getMonth()+1)+'-'+d.getDate(); if (!(ds in precipByDate)) { precipByDate[ds] = 0; } if (obs.precip_total) { precipByDate[ds] += obs.precip_total } }); } Object.entries(precipByDate).sort((a, b) => b[1] - a[1])[0] - ^
Looking at the 2000 election map in Florida, any good thunderstorm in the panhandle, in the northeast corner of the state, or on the west-middle-south of the peninsula would have done the trick.
- ^
https://en.wikipedia.org/wiki/1976_United_States_presidential_election -- Carter won Ohio and Wisconsin by 11k and 35k votes, respectively.
I think this argument is not sufficient. Turnout effects of weather can flip elections that are already close, and from our limited perspective, more than 0.1% of elections are close. But the question is asking about the 2028 election in particular, which will probably not be so close.
*
158I think I’m with Thomas Kwa on this one, mainly because I see 0.1% as a really low bar. E.g.
- let’s say ≥10% chance that the election is close enough to turn on “random-ish things” rather than “structural factors” (random-ish things would include [as discussed in other answers] weather on election day, decisions of particular individuals that “could have gone either way” [to run or not, to endorse or not, to assassinate or not, to release incriminating information on a candidate right before election day or not, whatever Patient Zero of COVID-19 was doing at the time], etc.);
- and out of those ≥10%, it seems reasonable to me to guess ≥1% chance that a re-roll of quantum randomness would flip the result.
So that gets us above 0.1%.
I think my guess would be more like, I dunno, 1%–10%?
111
In this very particular case, since chaotic variation of winds seem likely to be affected by QM, I think we can confidently say yes. From Metaculus
@Jgalt I did some research. The reporting is that the shooter was likely 150 yards away, so 137 meters), and the wind speed in Butler, PA during the rally was ~2-3m/s. Apparently at a range of 400m and 1m/s wind, bullets deflect by ~4 inches. So Trump's survival could have come down to simply the wind being favorable. Very very close call.
Eh, I don't buy it, or like, I think it's just restating the underlying question. My best guess is wind direction is pretty strongly overdetermined (like, even on just the extremely dumb first order approximation you can often get to 95%+ confidence about wind direction, because places tend to have pretty consistent wind patterns).
But even granting that, it's still not settled because there might be other reasons that would have overdetermined the outcome of the election. For example, it might be overdetermined that Trump dies before the election due to ol...
*
9-4I think "one of the potential candidates might quantum-randomly die in the timeframe" is a pretty strong argument that there's at least ~0.1% quantum uncertainty.
ETA: For some stats on this, see this table from the government of Canada. Annual death rate ranges from 0.1% for 35-year olds, up to 0.5% for 55-year-olds, and 3% for 75-year-olds. Multiply those by 4 to get the death rate in the relevant window. Obviously only a small fraction of those deaths will be quantum-randomness-influenced. Also note the relatively high rate of presidential assassinations -- 4 of 45(!) presidents were asssassinated in office(although I assume the "true" probability is lower now)
I don't think most people die for quantum-randomness reasons. I expect very little probability of someone dying is related to quantum randomness (though my guess is someone might disagree, but then we are just kind of back to the OP question about how much quantum randomness influences macro-level events).
40
Ok, so in the box of gas case, you have individual gas molecules following newtonian physics with no process to give any kind of structure at all. However, a human brain of a voter is more like an optimizing process. Most small perturbances to the "house" example, say you go nudge a 2x4 in the materials pile a tiny amount, which is much larger than quantum randomness, and the workers building the house will still put that piece of wood where it goes in the structure, or select an equivalent piece of wood which ends up forming the structure still.
Inside a human brain of a voter, including the primary voters who will determine the candidates for the 2028 election, there is an overall function the brain circuitry tries to satisfy, and many synaptic weights that encode policies that will attempt to satisfy that function. Small fluctuations from quantum randomness are unlikely to change voter preferences, since these are encoded by many weights that reflect life experiences etc. And you can empirically check this - look at experiments where people are presented with new evidence that challenges their currently held beliefs. Generally this just doesn't work, people interpret the new evidence to support their beliefs, even if a rational agent would not.
What about bigger trends, such as the price of gasoline, or economic activity and employment rates and relative spending power per voter? Same thing here, small quantum randomness is drowned out by larger macroscale trends and inertia, many of the fluctuations cancel out. As in, if you can "reroll" history, and the fluctuations have the same distribution as before, but a different random seed, many of these larger trends would happen identically to the original run.
What about historical events where critical decisions came down to the whim of one man? One of the famous ones being Hitler's choice of when to attack, allegedly years before his advisors recommended. Maybe. One theory is that Hitler personally had a terminal illness, and so this man would always order an early attack. You could not convince him not to attack with rational evidence or arguments on the probability of winning, because he would personally be dead and unable to see the outcome if the war were delayed.
The existence of the terminal illness would be known to an omniscient observer, and so this would be a case where a seeming "black swan" - an irrational early attack - would be predictable.
WW2 is a specific case where we know that the material advantages the winning side had were enormous, we know the ultimate winners, but tiny perturbations could have changed the course of entire campaigns.
I wonder what the margin of infection was for patient 0 in Wuhan...
agreed on most points, but 1. we're asking about 0.1% impact, and 2. optimizing processes can have multiple dynamical sinks, so the question is how often we cross decision boundaries in the aggregate dynamical system due to quantum randomness, and I expect the answer is often enough that it has more than 0.1% impact, because any time a chaotic system has the opportunity to make a difference in a person's behavior, the chaotic system will depend on a significant portion of the bits of the quantum system, and in particular that means the weather over a long ...
31
Daniel Kahneman notes that if sperm are randomized, the chance of Hitler, Stalin, and Mao all being born boys is 1/8. Re-run the 20th century with any of them being female and you get vastly different results. That thought experiment makes me suspect our intuitions for the inevitability of history are faulty.
22
I strongly feel Habryka is right here. Things are not that contingent. In particular, the invocation of chaos theory feels misleading here. The weather is chaotic on relevant timescales but most of our world and society is very much not.
Interested to hear different intuitions
Steve Byrnes argument seems convincing.
If there’s 10% chance that the election depends on an event which is 1% quantum-random (e.g. the weather) then the overall event is 0.1% random.
How far back do you think an omniscient-modulo-quantum agent could‘ve predicted the 2024 result?
2020? 2017? 1980?
The weather significantly impacts society, especially lately. Eg, to pick one kind of event, via wikipedia via IPCC report 2021:
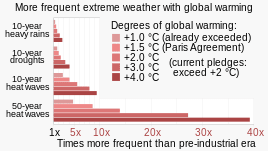
this has practical effects for a variety of parts of the economic network, notably shipping and natural disasters, both of which affect prices in ways that can affect what policies people want, as well as anyone who's directly impacted by a natural disaster.
-80
Perfect predictions of certain physical systems are downright impossible due to tipping points, ie chaos theory.
One relevant consideration: I used to make all sorts of everyday decisions via a quantum random number generator (specifically an app that would query this online source of quantum random numbers), and it wouldn't take that many people like me doing that to create pretty large butterfly effects.
This also provides a way for constructively lower-bounding it, which doesn't appeal to nebulous systems like weather or hard-to-estimate-quantum-contribution-to-even-in-principle things like whether leading candidates will drop dead of a heart attack or stroke or assassination before the election (surely a major consideration!). You can use quantum randomness to directly affect elections by amplifying your actions.
An example of this would be donor lotteries: pick your preferred candidate and commit $X to supporting them & affiliated groups; then take an efficient high-leverage lottery like forex options, and use a quantum random number generator to choose which one to buy, with a payoff of, say, 1000:1 (which should imply by EMH that it has roughly 1/1000 probability of paying off). You wipe out to $0 in 999 universes but then get 1000x in the last universe. In that universe, you donate it.*
Given assumptions about how much money you start with, how much leverage you choose, and the elasticity of donation for victory, this implies that there must be at least a certain amount of quantum uncertainty in who wins. I think with plausible values, you still get a quantum uncertainty which doesn't require too many zeros after the decimal point to write down, so that's useful: if even a single person could have that much quantum-influence if they wanted... And the more people who do this, the more the quantum-ness goes up even if the actions sometimes cancel out.
(Using made-up numbers: If I commit $1m and I believe that $1000m in donations 100% guarantees victory to my favored candidate who has a 50% chance right now and I use 1:1000 leverage, then 1/1000th of the time quantum randomness means the candidate goes from 50% to 100% (because I hit the jackpot & donate & they win), so there must be at least 1/1000 * (100-50) = 0.05% quantum randomness in who wins, where even an otherwise omniscient predictor is unsure because they can't know if we'll end up in the 999 baseline universes or the 1 quantum fluke universe. They may be 99.95% sure the other candidate will win for reasons not apparent to us, but not 100% sure.)
* There are a few stories floating around of people doing things like this, so it's not necessarily even that wacky a strategy.
Gwern, this only kingmakes if there is one player able to decide the election on their own by quantum dice.
What happens when there is 100 large entities doing this? 10,000? Law of large numbers would apply here.
Law of large numbers would apply here.
To the convergence to the classical probability, but it doesn't wash away the quantumness. The quantumness doesn't go away when you add more quantumness (barring specific setups like interference or spooky action where you've carefully created correlations/anti-correlations between the quantum randomness, of course). If I flip 1 classical coin for an expected 0.5 heads, that is less quantum than if I flip 1 classical coin and 1 quantum coin and average, and less quantum than if I clip 1 classical coin and 999 quantum coins and average, even though per CLT the second will be tighter around 0.5 and the third will be much tighter around 0.5.
Sure. Main thing is the election results are about the same, just a list of names of which 'quantum die rolling organization' supported candidate A, and who supported B, has many differences.
Or in your coin example, universe 1 might be HHTTHTHT and universe 2 might be THTHHTHT , but the totals are almost the same.
I do think even if you change the outcome of all people using quantum random number generators, this is quite unlikely to flip the outcome of an election. It's just not that many people, and election margins are quite large. There are butterfly effects here, but I think the prior on the people who use quantum random number generators explaining a lot of the variance of election outcomes seems quite unlikely to me, even if you can correlate their actions somehow.
edit: this is a reply to the wrong thread.
among other ways to have an effect, it just has to change the economic fortunes of enough people for their policy preferences to change, which depends on how the overall system's dynamics respond to the randomness. if it's overall mostly a sink towards a particular outcome, then you might be right, but it seems to me that chaos has a pretty significant impact in which natural disasters happen, which ought to have a significant impact on economic fortunes.
Looking just at one particular mechanism: how often will weather counterfactually impact the outcome of an election? Presumably only if the election is very close, but seems very plausible for e.g. the 2000 election, so it's not that rare, though definitely not the norm. Conservatively call it one election in 50 sensitive to the weather? (I expect it should be much higher than that given how recent 2000 was, but I'm trying to get a lower bound here.)
... and I'd be very surprised if weather isn't mostly-quantum-randomized on a four year timescale.
So I'd expect that at least one in fifty elections is counterfactually sensitive to quantum noise.
On the other hand, most elections are not that close, and I'd expect that even a moderately-stronger-than-human AI could usually guess pretty confidently in advance which elections will and won't be that close.
For elections which aren't unusually close, are the tail probabilities sensitive to quantum noise? I'd be surprised if they were; central limit theorem bites hard at the scale of elections. With a hundred million voters we're talking about standard error on the scale of ten thousand, or 0.01% of the electorate... and e.g. the 2020 election had ~4.5% advantage for Biden according to wikipedia... so that's hundreds of standard deviations. (Though admittedly that's ignoring the electoral college, which could definitely have weird effects.) So quantum noise would have to have, not just local effects in a few places, but huge correlated effects over a large chunk of the electorate in order have appreciable effects on the election counts themselves.
Impact on individual candidates is maybe more plausible? Not sure what specific mechanisms would be relevant there. E.g. interstice's suggestion of a candidate randomly dying seems probably less than 0.1% probable in a typical election? Based on a quick google someone 65-75 years old has roughly a 0.8% chance of dying over four years, it will be an OOM lower for younger candidates, and even for old candidates most of that probability will be packed in health problems which can be seen coming well in advance if one is looking for them.
Let me try to state this problem a little more precisely. (And I'll frame it in terms of this year's election.)
Using Newtonian mechanics, we can calculate where the Earth should be (relative to some galactic coordinate system) on election day 2024. Then consider the past light-cone of that Earth, back to the present day, the end of January. That's covers a region of space about ten light-months around the solar system.
We are asking: Suppose we knew the quantum state of that 20-light-month-diameter region of space, as precisely as possible. What is the uncertainty in the outcome of the 2024 election, 10 months in the future?
I think the uncertainty is pretty large, because quantum uncertainty isn't just in radioactive decays, it's in every emission of a photon from an excited atom or molecule. We are surrounded by an ocean of quantum thermal noise. And so any dynamical system which chaotically amplifies microscopic differences, will be amplifying that ubiquitous quantum thermal uncertainty. This is definitely the case for fluids like the atmosphere, and it must surely be the case for biological decision makers made out of neurons, even if it is filtered by canalization of neural and cognitive dynamics. There would be other macroscopic material processes in which quantum uncertainty gets amplified, e.g. fractures in solids under stress. (It would be interesting to calculate the role of amplified quantum uncertainty in earthquakes!)
My proposition is, that in a quantum world, exact microscopic knowledge of the physical state of the world, may do nothing to reduce the uncertainty of an event like an election. That may be overstating a little, because better knowledge of people and the world and the events that might come to pass in the remaining months, can reduce the uncertainty. But in systems which are authentically chaotic or dynamically unstable, the quantum uncertainty in initial conditions has exactly the same effect as merely epistemic uncertainty - it renders the future unpredictable.
If you throw a trillion dice, each face comes up almost precisely one sixth of the time. In this case, the width of the distribution shrinks rather than grows with the number of random variables you add up.
Given a button that instantaneously inverts the momentum of every air molecule, how confident are you that pressing the button changes the outcome of the 2028 US presidential election?
At the risk of more downvotes, presumably for rejecting the hypothetical, I reject the hypothetical.
There's an uncomfortable (to me) dualism in this kind of question - the idea of an omnicient observer with that granularity implies non-embeddedness. It can't be INSIDE the volume under analysis AND contain more than itself in it's knowledge (and probably not even itself - there will be a loss in efficiency in legibilizing it's own state).
The obvious but unhelpful answer is "of course it's possible to calculate future states - the actual universe does make this calculation. However, it only reveals it internally in real-time (thus the term)".
The question as asked, though, is kind of nonsense. From inside, it's impossible to determine what's "quantum randomness" and what's plain old measurement/calculation error.
This is a relatively straightforward question in the context of quantum mechanics. There is a fact of the matter of how much amplitude the world states get where one person wins an election vs. the other one. This question is about how much such decoherence there will be.
In this conception of uncertainty there is no answer to the matter of which of the two outcomes really happens. Both events get some magical reality fluid, as Eliezer would call it.
I'm not sure there IS a fact of the matter, as far as any agent upstream of the macro-scale event will be able to measure. There is a mathematical abstraction about it that seems to match some extremely micro observations, but it's extremely unclear how that can be used to predict future experiences of instantiated beings.
I could see an argument that quantum randomness does not have a large effect for the particular election in 2028, as long as no one is actively trying to make this prediction wrong. I have no idea about US politics right now, so I have no clue if it is already foreseeable that margins are going to be large.
At least the election in 2000 would fail this test, though (As discussed on Metaculus). Weather alone could have turned things around on election day would be my guess. First past the post voting makes close margins more likely, and the electoral college makes that different weather in just 1 large swing state can turn things around.
One thing I find interesting how the US election is probably a big amplifier of the relevance of quantum randomness in a lot of other areas. Makes me wonder if there are other identifiable sources of chaos amplification that I don't have on my radar yet. Perhaps the spread of memes? Especially since politics is operating so much on level 4. I would guess there would be memes that once around would not be as easily be affected through equal and opposite effects.