As I said in a comment at the GiveWell blog, a normal prior would assign vanishing probability to the existence of charities even 10x better than 90th percentile charitable expenditures (low-value first world things). Vaccinations appear to do many times better, and with the benefit of hindsight we can point to particular things like smallpox eradication, the Green Revolution, etc. But if we had a normal prior we would assign ludicrously low probability (less than 10^-100 probability) to these things having been real, too small to outweigh the possibility of hoax or systematic error. As Eliezer said in the previous thread, if a model assigns essentially zero probability to something that actually happens frequently, it's time to pause and recognize that the model is terribly wrong:
This jumped out instantly when I looked at the charts: Your prior and evidence can't possibly both be correct at the same time. Everywhere the prior has non-negligible density has negligible likelihood. Everywhere that has substantial likelihood has negligible prior density. If you try multiplying the two together to get a compromise probability estimate instead of saying "I notice that I am confused", I would hold this up as a pretty strong example of the real sin that I think this post should be arguing against, namely that of trying to use math too blindly without sanity-checking its meaning.
In the context of existential risk, Holden has claimed that expected QALYs of x-risk reductions are low, so that even aggregative utilitarian types would do badly on x-risk vs vaccinations. Given that there are well-understood particular risks and ways of spending on them (and historical examples of actual progress, e.g. tracking 90% of dinosaur killer asteroids and now NEA ) this seems to require near-certainty that humanity will soon go extinct anyway, or fail to colonize space or create large populations, so that astronomical waste considerations don't loom large.
This gives us a "Charity Doomsday Argument": if humanity could survive to have a long and prosperous future, then at least some approaches to averting catastrophes would have high returns in QALYs per dollar. But by the normal prior on charity effectiveness, no charity can have high cost-effectiveness (with overwhelming probability), so humanity is doomed to catastrophe, stagnation, or an otherwise cramped future.
ETA: These problems are less severe with a log-normal prior (the Charity Doomsday Argument still goes through, but the probability penalties for historical interventions are less severe although still rather heavy), and Holden has mentioned the possibility of instead using a log-normal prior in the previous post.
This post massively increased my confidence in GiveWell's opinions by asking and answering intelligent, relevant questions very clearly.
The post would be even stronger if it addressed Carl Shulman's concern about how to handle non-tiny likelihoods that a charity is more than 10x better than, say, the United Way of Massachusetts. Log-normal distributions would help, but I think sometimes an initial estimate provides evidence that a charity is either extremely effective (>3X) or not very effective (<0). E.g. if I tell you that my charity has invented a safe and effective vaccine for HIV that can be manufactured and distributed for $20 a dose, and is currently seeking funds to distribute the vaccine, I am probably either (a) lying, (b) woefully misinformed, (c) contributing to Malthusian doom, or (d) running an absurdly effective charity. These four options probably account for the vast majority of the probability distribution. I would expect the amount of probability left over to be tiny -- the probability that i have instead invented, e.g., a risky and sometimes effective vaccine for HIV that can be manufactured and distributed for $4,000 per dose is pretty small. For this kind of situation, it wouldn't make sense to model the probability as continuously declining above 0.5X -- you would want most of the probability to hover around 0, and a little bit of probability to hover around 3X (or whatever figure you would adopt if my claims proved to be correct). There would be some probability at X and 2X -- but not much; the distribution would have two peaks, not one peak.
I think a lot of the work here is being done by the assumption that the standard deviation of the estimate error depends on (and, moreover, is linear in terms of!) the estimate itself.
Why would we assume this?
Holden suggests that this is reasonable since it keeps the probability of the "right estimate" being zero constant. This seems bizarre to me: no matter how huge my estimate is, there's a constant chance that it's completely off? And surely, one would expect the chance of the "correct" estimate being zero to be much higher in cases where your own estimate is close to zero.
The only other motivation I can think of is that we ought to be more suspicious of higher estimates. Hence, if we come up with a high estimate, we should be suitably suspicious and assume our estimate had a high error. But surely this "suspicion of high estimates" is precisely encoded in our prior; that is, before estimation we believe that a higher value is less likely, and our prior distribution reflects that. But then why are we adding an additional fudge factor in the form of an increased estimate error?
Even if we were convinced that we should assign higher standard deviation to the error on higher estimates, it seems far from obvious that this should be linear in our estimate!
Additionally, I'm not sure that a normal distribution is the correct distribution for healthcare charities, at least. The DCP2 data strongly suggests that the underlying distribution is log-normal. Even though DCP2 has been shown to be a lot less reliable than we'd like (here; some great work by GiveWell, if I may say so!), the sample size is large enough that we wouldn't expect errors to change the underlying distribution.
Interesting but from a purely mathematical pov I've some problems with the model (or the way it's used).
The article doesn't speak at all of cases where the initial estimate is negative (you can have an initially, broad estimate, of a charity to be negative, that is, below average, even if at the end it's an efficient one).
Variance of error = estimate sounds too drastic to me. It's reasonable to assume that, since your estimate is crude, it'll tend to be more error-prone when extreme. But first, if your first estimate is very close to "oh, this charity seems really average" (X very close to 0) that doesn't mean it that the error in the estimate is very close to 0. And then, even if your estimate is crude, it's still comes from some information, not pure random. What about something like 1+aX as the variance of error (with a somewhere like 3/4 maybe) ? So it never gets close to 0, and you still account for some amount of information in the estimate. I'm popping the formula out of my head. A much better one could probably be done using bits of information : ie, your estimate is worth one bit of information, and using Bayes' theorem you unfold the error estimate with a prior of (0,1) to get to (X,Y) with fixed X and one bit of information... something like that ?
Assuming you always get the same X for all of your crude estimates seem very unlikely - I can understand it's a simplifying hypothesis, but more realistic hypothesis where you get different values of X for different estimates of the same charity should be analyzed too... will it be the topic of the next article ?
And finally (but it's just a wording issue) you seem to confuse "will be 0" and "will be 0 or less" in the text, for example : « it has a normally distributed "estimate error" with mean 0 (the estimate is as likely to be too optimistic as too pessimistic) and standard deviation X (so 16% of the time, the actual impact of your $1000 will be 0 or "average"). » well, it's "will be 0 or less" in that. you'll never get exactly 0 using continuous functions.
A few quick notes:
As I wrote in my response to Carl on The GiveWell Blog, the conceptual content of this post does not rely on the assumption that the value of donations (as measured in something like "lives saved" or "DALYs saved") is normally distributed. In particular, a lognormal distribution fits easily into the above framework. .
I recognize that my model doesn't perfectly describe reality, especially for edge cases. However, I think it is more sophisticated than any model I know of that contradicts its big-picture conceptual conclusions (e.g., by implying "the higher your back-of-the-envelope [extremely error-prone] expected-value calculation, the necessarily higher your posterior expected-value estimate") and that further sophistication would likely leave the big-picture conceptual conclusions in place.
JGWeissman is correct that I meant "maximum" when I said "inflection point."
I recognize that my model doesn't perfectly describe reality, especially for edge cases
The model is uninteresting for cases within a standard deviation of the mean, so that's an enormous weakness, particularly as edge cases have happened before in history.
This is in some ways a counterintuitive result...further sophistication would likely leave the big-picture conceptual conclusions in place.
It's counterintuitive because you represented the mathematical model as one modeling reality. It's not counterintuitive if one only thinks about the math.
If the model gets correct conclusions for the questions you are interested in but doesn't describe reality well, it doesn't need more sophistication - it needs replacement.
However, "the higher the initial estimate of cost-effectiveness, the better" is not strictly true.
This is because absence of evidence is evidence of absence, not because in the real world one is confronted by anything resembling the situation where initial expected estimates of charities' effectiveness have "...a normally distributed "estimate error" with mean 0 (the estimate is as likely to be too optimistic as too pessimistic) and...hold the 'probability of 0 or less' constant."
when I think about how to improve the robustness of evidence and thus reduce the variance of "estimate error," I think about examining a charity from different angles - asking critical questions and looking for places where reality may or may not match the basic narrative being presented.
This works because the final estimated expected value punishes charities for being unable to provide good accounts of their estimates; the absence of such accounts by those most motivated and in the best position to provide them is evidence that they do not exist.
Possibly, charities with particular high initial estimated expected values have historically done worse than those with specific lower initial estimated expected values - I would wager that this is in fact true for some values. If so, this alone provides reason to disbelieve similar high initial estimated expected values independent of statistical chicanery pretending that in reality there is no relationship between charities' initial expected value and the chance that they are no better than average.
Thank you. This is exactly the kind of posts I want to read on lesswrong, not more vague philosophizing on subjects which have been covered hundreds of times before.
This model doesn't seem to work well for extreme values. Most illustratively if gives zero for infinite outcomes. Zero is not a probability.
Not in my comfort zone here, but surely you have to allow for probabilities of 0 when building any formal mathematical system. P(A|~A) has to be 0 or you can't do algebra. As an agent viewing the system on a meta level, I can't assign a personal probability of 0 to any proof, but within the system it needs to be allowable.
Much discussion of this generally and this point in particular.
I don't know that the results there are necessarily correct, but they are certainly relevant.
It's not a probable outcome, but there literally is no such thing as an impossible outcome.
You donate to the Corrupt Society For Curing Non-existent Diseases in Cute Kittens, the money is used for hallucinogens, the hallucinogens are found by the owners kid, who when high comes up with a physics kitchen experiment which creates an Zeno Machine, and mess around with it randomly. This turns out to simulate an infinite amount of infinitely large cheesecakes, and through a symbolism that you haven't learnt about yet simulated chesecakes have according to your utility function an utility equal to the logarithm of their weight in solar masses.
Who said my utility function was unbounded? (Which, BTW, is the same as my reply to the Pascal's Mugger in the wording “create 3^^^3 units of disutility”.)
If you're going to have a probability distribution that covers continuous intervals, 0 has to be allowed as a probability.
That just looks like a proof you can't have probability distributions over continuous intervals.
0 shouldn't be assigned as a probability if you're going to do Bayesian updates. That doesn't interfere with the necessity of using 0 when assigning probabilities to continuous distributions, as any evidence you have in practice will be at a particular precision.
For example, say the time it takes to complete a task is x. You might assign a probability of 20% that the task is finished between 2.3 and 2.4 seconds, with an even distribution between. Then, the probability that it is exactly 2.35 seconds is 0; however, the measured time might be 2.3500 seconds to the precision of your timing device, whose prior probability would be .02%.
Edit: I need a linter for these comments. Where's the warning "x was declared but never used"?
I know that. But any possible interval must be non-zero.
Also, some exact numbers are exceptions, depending on how you measure things: for example, there is a possibility the "task" "takes" EXACTLY 0 seconds, because it was already done. For example, sorting something that was already in the right order. (In some contexts. In other contexts it might be a negative time, or how long it took to check that it really was already done, or something like that)
Infinite utility seems like it might be a similar case.
I am cross-posting this GiveWell Blog post, a followup to an earlier cross-post I made. Here I provide a slightly more fleshed-out model that helps clarify the implications of Bayesian adjustments to cost-effectiveness estimates. It illustrates how it can be rational to take a "threshold" approach to cost-effectiveness, asking that actions/donations meet a minimum bar for estimated cost-effectiveness but otherwise focusing on robustness of evidence rather than magnitude of estimated impact.
We've recently been writing about the shortcomings of formal cost-effectiveness estimation (i.e., trying to estimate how much good, as measured in lives saved, DALYs or other units, is accomplished per dollar spent). After conceptually arguing that cost-effectiveness estimates can't be taken literally when they are not robust, we found major problems in one of the most prominent sources of cost-effectiveness estimates for aid, and generalized from these problems to discuss major hurdles to usefulness faced by the endeavor of formal cost-effectiveness estimation.
Despite these misgivings, we would be determined to make cost-effectiveness estimates work, if we thought this were the only way to figure out how to allocate resources for maximal impact. But we don't. This post argues that when information quality is poor, the best way to maximize cost-effectiveness is to examine charities from as many different angles as possible - looking for ways in which their stories can be checked against reality - and support the charities that have a combination of reasonably high estimated cost-effectiveness and maximally robust evidence. This is the approach GiveWell has taken since our inception, and it is more similar to investigative journalism or early-stage research (other domains in which people look for surprising but valid claims in low-information environments) than to formal estimation of numerical quantities.
The rest of this post
Conceptual illustration
I previously laid out a framework for making a "Bayesian adjustment" to a cost-effectiveness estimate. I stated (and posted the mathematical argument) that when considering a given cost-effectiveness estimate, one must also consider one's prior distribution (i.e., what is predicted for the value of one's actions by other life experience and evidence) and the variance of the estimate error around the cost-effectiveness estimate (i.e., how much room for error the estimate has). This section works off of that framework to illustrate the potential importance of examining charities from multiple angles - relative to formally estimating their cost-effectiveness - in low-information environments.
I don't wish to present this illustration either as official GiveWell analysis or as "the reason" that we believe what we do. This is more of an illustration/explication of my views than a justification; GiveWell has implicitly (and intuitively) operated consistent with the conclusions of this analysis, long before we had a way of formalizing these conclusions or the model behind them. Furthermore, while the conclusions are broadly shared by GiveWell staff, the formal illustration of them should only be attributed to me.
The model
Suppose that:
The implications
I use "initial estimate" to refer to the formal cost-effectiveness estimate you create for a charity - along the lines of the DCP2 estimates or Back of the Envelope Guide estimates. I use "final estimate" to refer to the cost-effectiveness you should expect, after considering your initial estimate and making adjustments for the key other factors: your prior distribution and the "estimate error" variance around the initial estimate. The following chart illustrates the relationship between your initial estimate and final estimate based on the above assumptions.
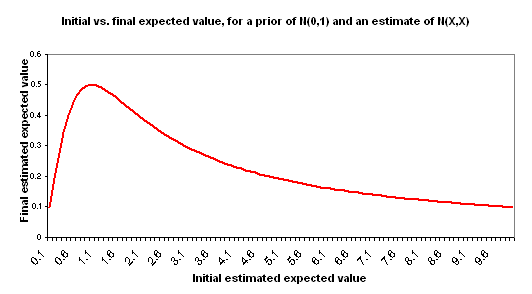
Note that there is an inflection point (X=1), past which point your final estimate falls as your initial estimate rises. With such a rough estimate, the maximum value of your final estimate is 0.5 no matter how high your initial estimate says the value is. In fact, once your initial estimate goes "too high" the final estimated cost-effectiveness falls.
This is in some ways a counterintuitive result. A couple of ways of thinking about it:
Now suppose that you make another, independent estimate of the good accomplished by your $1000, for the same charity. Suppose that this estimate is equally rough and comes to the same conclusion: it again has a value of X and a standard deviation of X. So you have two separate, independent "initial estimates" of good accomplished, and both are N(X,X). Properly combining these two estimates into one yields an estimate with the same average (X) but less "estimate error" (standard deviation = X/sqrt(2)). Now the relationship between X and adjusted expected value changes:
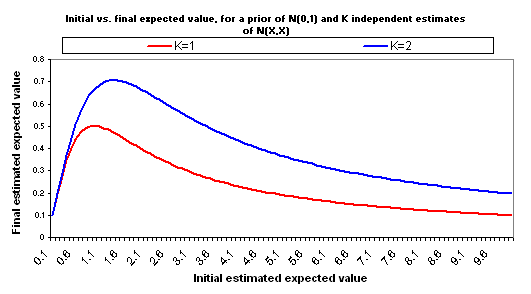
Now you have a higher maximum (for the final estimated good accomplished) and a later inflection point - higher estimates can be taken more seriously. But it's still the case that "too high" initial estimates lead to lower final estimates.
The following charts show what happens if you manage to collect even more independent cost-effectiveness estimates, each one as rough as the others, each one with the same midpoint as the others (i.e., each is N(X,X)).
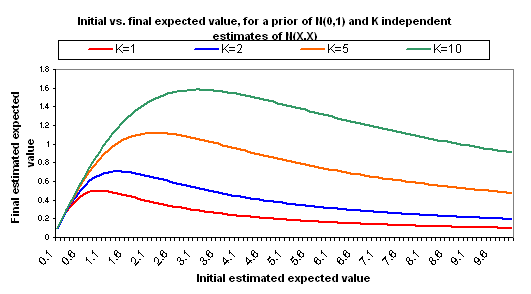
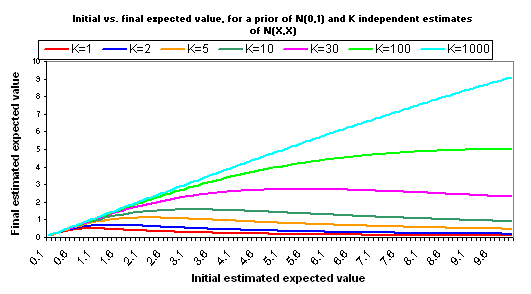
The pattern here is that when you have many independent estimates, the key figure is X, or "how good" your estimates say the charity is. But when you have very few independent estimates, the key figure is K - how many different independent estimates you have. More broadly - when information quality is good, you should focus on quantifying your different options; when it isn't, you should focus on raising information quality.
A few other notes:
Instead, when I think about how to improve the robustness of evidence and thus reduce the variance of "estimate error," I think about examining a charity from different angles - asking critical questions and looking for places where reality may or may not match the basic narrative being presented. As one collects more data points that support a charity's basic narrative (and weren't known to do so prior to investigation), the variance of the estimate falls, which is the same thing that happens when one collects more independent estimates. (Though it doesn't fall as much with each new data point as it would with one of the idealized "fully independent cost-effectiveness estimates" discussed above.)
While other distributions may involve later/higher inflection points than normal distributions, the general point that there is a threshold past which higher initial estimates no longer translate to higher final estimates holds for many distributions.
The GiveWell approach
Since the beginning of our project, GiveWell has focused on maximizing the amount of good accomplished per dollar donated. Our original business plan (written in 2007 before we had raised any funding or gone full-time) lays out "ideal metrics" for charities such as
Early on, we weren't sure of whether we would find good enough information to quantify these sorts of things. After some experience, we came to the view that most cost-effectiveness analysis in the world of charity is extraordinarily rough, and we then began using a threshold approach, preferring charities whose cost-effectiveness is above a certain level but not distinguishing past that level. This approach is conceptually in line with the above analysis.
It has been remarked that "GiveWell takes a deliberately critical stance when evaluating any intervention type or charity." This is true, and in line with how the above analysis implies one should maximize cost-effectiveness. We generally investigate charities whose estimated cost-effectiveness is quite high in the scheme of things, and so for these charities the most important input into their actual cost-effectiveness is the robustness of their case and the number of factors in their favor. We critically examine these charities' claims and look for places in which they may turn out not to match reality; when we investigate these and find confirmation rather than refutation of charities' claims, we are finding new data points that support what they're saying. We're thus doing something conceptually similar to "increasing K" according to the model above. We've recently written about all the different angles we examine when strongly recommending a charity.
We hope that the content we've published over the years, including recent content on cost-effectiveness (see the first paragraph of this post), has made it clear why we think we are in fact in a low-information environment, and why, therefore, the best approach is the one we've taken, which is more similar to investigative journalism or early-stage research (other domains in which people look for surprising but valid claims in low-information environments) than to formal estimation of numerical quantities.
As long as the impacts of charities remain relatively poorly understood, we feel that focusing on robustness of evidence holds more promise than focusing on quantification of impact.
*This implies that the variance of your estimate error depends on the estimate itself. I think this is a reasonable thing to suppose in the scenario under discussion. Estimating cost-effectiveness for different charities is likely to involve using quite disparate frameworks, and the value of your estimate does contain information about the possible size of the estimate error. In our model, what stays constant across back-of-the-envelope estimates is the probability that the "right estimate" would be 0; this seems reasonable to me.