(This is a long post. If you’re going to read only part, please read sections 1 and 2, subsubsection 5.6.2, and the conclusion.)
1. Introduction
Suppose you want to give some money to charity: where can you get the most bang for your philanthropic buck? One way to make the decision is to use explicit expected value estimates. That is, you could get an unbiased (averaging to the true value) estimate of what each candidate for your donation would do with an additional dollar, and then pick the charity associated with the most promising estimate.
Holden Karnofsky of GiveWell, an organization that rates charities for cost-effectiveness, disagreed with this approach in two posts he made in 2011. This is a response to those posts, addressing the implications for existential risk efforts.
According to Karnofsky, high returns are rare, and even unbiased estimates don’t take into account the reasons why they’re rare. So in Karnofsky's view, our favorite charity shouldn’t just be one associated with a high estimate, it should be one that supports the estimate with robust evidence derived from multiple independent lines of inquiry.1 If a charity’s returns are being estimated in a way that intuitively feels shaky, maybe that means the fact that high returns are rare should outweigh the fact that high returns were estimated, even if the people making the estimate were doing an excellent job of avoiding bias.
Karnofsky’s first post, Why We Can’t Take Expected Value Estimates Literally (Even When They’re Unbiased), explains how one can mitigate this issue by supplementing an explicit estimate with what Karnofsky calls a “Bayesian Adjustment” (henceforth “BA”). This method treats estimates as merely noisy measures of true values. BA starts with a prior representing what cost-effectiveness values are out there in the general population of charities, then the prior is updated into a posterior in standard Bayesian fashion.
Karnofsky provides some example graphs, illustrating his preference for robustness. If the estimate error is small, the posterior lies close to the explicit estimate. But if the estimate error is large, the posterior lies close to the prior. In other words, if there simply aren’t many high-return charities out there, a sharp estimate can be taken seriously, but a noisy estimate that says it has found a high-return charity must represent some sort of fluke.
Karnofsky does not advocate a policy of performing an explicit adjustment. Rather, he uses BA to emphasize that estimates are likely to be inadequate if they don’t incorporate certain kinds of intuitions — in particular, a sense of whether all the components of an estimation procedure feel reliable. If intuitions say an estimate feels shaky and too good to be true, then maybe the estimate was noisy and the prior is more important. On the other hand, if intuitions say an estimate has taken everything into account, then maybe the estimate was sharp and outweighs the prior.
Karnofsky’s second post, Maximizing Cost-Effectiveness Via Critical Inquiry, expands on these points. Where the first post looks at how BA is performed on a single charity at a time, the second post examines how BA affects the estimated relative values of different charities. In particular, it assumes that although the charities are all drawn from the same prior, they come with different estimates of cost-effectiveness. Higher estimates of cost-effectiveness come from estimation procedures with proportionally higher uncertainty.
It turns out that higher estimates aren’t always more auspicious: an estimate may be “too good to be true,” concentrating much of its evidential support on values that the prior already rules out for the most part. On the bright side, this effect can be mitigated via multiple independent observations, and such observations can provide enough evidence to solidify higher estimates despite their low prior probability.
Charities aiming to reduce existential risk have a potential claim to high expected returns, simply because of the size of the stakes. But if such charities are difficult to evaluate, and the prior probability of high expected values is low, then the implications of BA for this class of charities loom large.
This post will argue that competent efforts to reduce existential risk reduction are still likely to be optimal, despite BA. The argument will have three parts:
-
BA differs from fully Bayesian reasoning, so that BA risks double-counting priors.
-
The models in Karnofsky’s posts, when applied to existential risk, boil down to our having prior knowledge that the claimed returns are virtually impossible. (Moreover, similar models without extreme priors don’t lead to the same conclusions.)
-
We don’t have such prior knowledge. Extreme priors would have implied false predictions in the past, imply unphysical predictions for the future, and are justified neither by our past experiences nor by any other considerations.
Claim 1 is not essential to the conclusion. While Claim 2 seems worth expanding on, it’s Claim 3 that makes up the core of the controversy. Each of these concerns will be addressed in turn.
Before responding to the claims themselves, however, it’s worth discussing a highly simplified model that will illustrate what Karnofsky’s basic point is.
2. A Simple Discrete Distribution of Charitable Returns
Suppose you’re considering a donation to the Center for Inventing Metawidgets (CIM), but you'd like to perform an analysis of the properties of metawidgets first.2 Before the analysis, you’re uncertain about three possibilities:
- With a probability of 4999 out of 10,000, metawidgets aren’t even a thing. You can’t invent what isn’t a thing, so the return is 0.
- With a probability of 5000 out of 10,000, metawidgets are a thing with some reasonably good use, like repairing printers. The return in this case is 1.
- With a probability of 1 out of 10,000, metawidgets have extremely useful effects, like curing lung cancer. Then the return is 100.
If we now compute the expected value of a donation to CIM, it ends up as a sum of the following components:
- 0.4999 * 0 = 0 from the possibility that the return is 0
- 0.5 * 1 = 0.5 from the possibility that the return is 1
- 0.0001 * 100 = 0.01 from the possibility that the return is 100
In particular, the possibility of a modest return contributes 50 times the expected value of the possibility of an extreme return. The size of the potential return, in this case, didn’t make up for its low probability.
But that’s before you do an analysis that will give you some additional evidence about metawidgets. The analysis has the following properties:
- Whatever the true return is, 50% of the time the analysis is correct and gives you the correct answer.
- If the analysis is wrong, it picks one of the three possible answers uniformly at random.
What happens if the analysis says the return is 100?
To find the right probabilities to assign, we have to do Bayesian updating on this analysis result. The outcome of the analysis is four times as likely if the true value is 100 than if it is either 0 or 1. So the ratio of the expected value contributions changes from 50:1 to 50:4.
Applied to this case, Karnofsky’s point is simply this: despite the analysis suggesting high returns, modest returns still come with higher expected value than high returns. High returns should be considered more probable after the analysis than before — we’ve observed a pretty good likelihood ratio of evidence in their favor — but high returns started out so improbable that even after receiving this bump, they still don’t matter.
Now that we’ve seen the point in simplified form, let’s begin a more detailed discussion.
3. The Role of BA
This section will add some critical notes on the concept of BA — notes that should apply whether the adjustment is performed explicitly or just used as a theoretical justification for listening to intuitions about the accuracy of particular estimates.
Before discussing the role of BA, let’s guard against a possible misinterpretation. Karnofsky is not arguing against maximizing expected value. He is arguing against a particular estimation method he labels “Explicit Expected Value,” which he considers to give inaccurate answers.
The Explicit Expected Value (EEV) method is simple: obtain an estimate of the true cost-effectiveness of an action, then act as if this estimate is the “true” cost-effectiveness. This “true” cost-effectiveness could be interpreted as an expected value itself.3
In contrast to EEV, Karnofsky advocates “Bayesian Adjustment.” Bayesian reasoning involves multiplying a prior by a likelihood to find a posterior. In this case, the prior describes the charities that are out there in the population; the likelihood describes how likely different true values would have been to produce the given estimate; and the posterior represents our final beliefs about the charity’s true cost-effectiveness. By looking at how common different effectiveness levels are, and how likely they would have been to lead to the given estimate, we judge the probability of various effectiveness levels.
In the sense that we’re updating on evidence according to Bayes’ theorem, what’s going on is indeed "Bayesian." But it’s worth pointing out one difference between Karnofsky’s adjustments and a fully Bayesian procedure: BA updates on a point estimate rather than on the full evidence that went into the point estimate.
This matters in two different ways.
First, the point estimate doesn’t always carry all the available information. A procedure for generating a point estimate from a set of evidence could summarize different possible sets of evidence into the same point estimate, even though they favor different hypotheses. This sort of effect will probably be irrelevant in practice, but one might call BA “half-Bayesian” in light of it.
Second, and more importantly, there’s a risk of misinterpreting the nature of the estimate. Karnofsky’s model, again, assumes that estimates are "unbiased" — that conditional on any given number being the true value, if you make many estimates, they’ll average out to that number. And if that’s actually the case for the estimation procedure being used, then that’s fine.
However, to the extent that an estimate took into account priors, that would make it “biased” toward the prior. As Oscar Cunningham comments:
The people giving these estimates will have already used their own priors, and so you should only adjust their estimates to the extent to which your priors differ from theirs.
In the most straightforward case, the source simply gave his own Bayesian posterior mean. If you and the source had the same prior, then your posterior mean should be the source’s posterior mean. After all, the source performed just the same computation that you would.
An old OvercomingBias post advises us to share likelihood ratios, not posterior beliefs. To be fair, in many cases communicating likelihood ratios for the whole space of hypotheses is impractical. One may instead want to communicate a number as a summary. (Even if one is making the estimate oneself, it may not be clear how one’s brain came up with a particular number.) But it’s important not to take a number that has prior information mixed in, and then interpret it as one that doesn’t.
In less straightforward cases, maybe part of the prior was taken into account. For example, maybe your source shares your pessimism about the organizational efficiency of nonprofits, but not your pessimism in other areas. Even if your source informally ignored lines of reasoning that seemed to lead to an estimate that was “too good to be true,” that is enough to make double-counting an issue.
But to put this section in context, the appropriateness of BA isn’t the most important disagreement with Karnofsky. Based on the considerations given here, performing an intuitive BA may well be better than going by an explicit estimate. Differences in priors have room to be far more important than just the results of (partially) double-counting them. So the more important part of the argument will be about which priors to use.
4. Probability Models
4.1: The first model
Karnofsky defends his conclusions with probabilistic models based on some mathematical calculations by Dario Amodei. This section will argue that these models only rule out optimal existential risk charity because the priors they assign to the relevant hypotheses are extremely low — in other words, because they virtually rule out extreme returns in advance.
In the model in Karnofsky’s first post, it’s easy to see the low priors. Consider the first example (the graphs are from Karnofsky's posts):
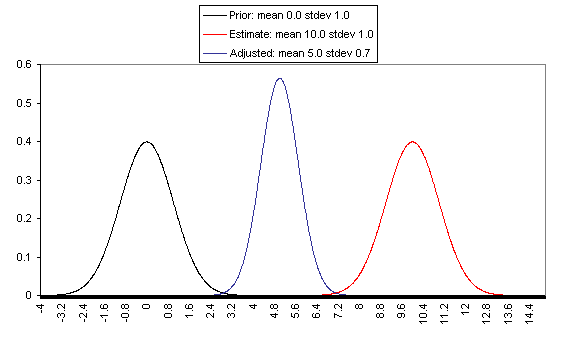
This example comes with some particular assumptions about parameters. The prior is normally distributed with mean 0 and standard deviation 1; the likelihood is normally distributed with mean 10 and standard deviation 1. As in the saying that “a Bayesian is one who, vaguely expecting a horse, and catching a glimpse of a donkey, strongly believes he has seen a mule,” the posterior ends up in the middle, hardly overlapping with either. As Eliezer Yudkowsky points out, this lack of overlap should practically never happen. When it does, such an event is a strong reason to doubt one’s assumptions. It suggests that you should have assigned a different prior.
Or maybe, instead of the prior, it’s the likelihood that you should have assigned differently — as one of the other graphs does:
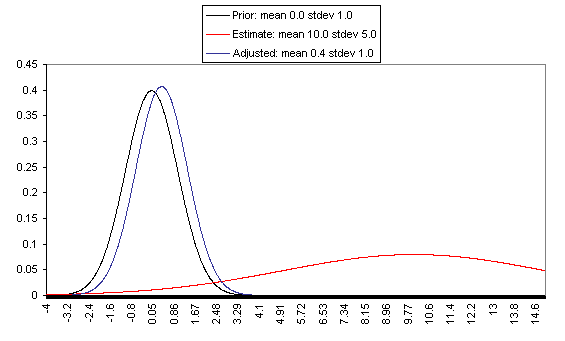
Here, the outcome makes some sense, because there’s significant overlap. A high true cost-effectiveness would have been more likely to produce the estimate found, but a low true cost-effectiveness could have produced it instead. And the prior says the latter case, where the true cost-effectiveness is low, is far more likely — so the final best estimate, indeed, ends up not differing much from the initial best estimate.
Note, however, that this prior is extremely confident. The difference in probability density between the expected value and a value ten standard deviations out is a factor of e-50, or about 10-22. This number is so low it might as well be zero.
4.2: The second model
The second model builds on the first model, so many of the same considerations about extreme priors will carry over. This time, we’re looking at a set of different estimates that we could be updating on like we did in the first model. For each of these, we take the expectation of the posterior distribution for the true cost-effectiveness, so we can put these expectations in a graph. After all, the expectation is the number that will factor into our decisions!
Here’s one of the graphs, showing initial estimates on the x-axis and final estimates on the y-axis. The initial estimates are what we’re performing a Bayesian update on, and the final estimates are the expectation value of the distribution of cost-effectiveness after updating:
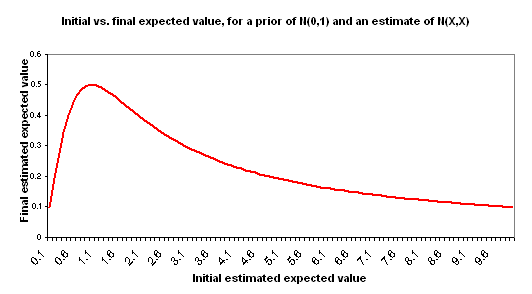
So as initial estimates increase, the final estimate rises at first, but then slowly declines. High estimates are good up to a point, but when they become too extreme, we have to conclude they were a fluke.
As before, this model uses a standard normal prior, which means high true values have enormously smaller prior probabilities. Compared to this prior, the evidence provided by each estimate is minor. If the estimate falls one standard deviation out in the distribution, then it favors the estimate value over a value of zero by a likelihood ratio of the square root of e, or about 1.65. So it’s no wonder that the tail end of high cost-effectiveness ends up irrelevant.
According to Karnofsky, this model illustrates that an estimate is safer to take at face value when evidence in its favor comes from multiple independent lines of inquiry. There are some calculations showing this — the more independent pieces of evidence for a given high value you gather, the more these together can overcome the “too good to be true” effect.
While multiple independent pieces of evidence are indeed better, it’s important to emphasize that the relevant variable is simply the evidence’s strength. Evidence can be strong because it comes from multiple directions, but it can also be strong because it just happens to be unlikely to occur under alternative hypotheses. If we have two independent observations that are both twice as likely to occur given cost-effectiveness 3 than cost-effectiveness 1, that’s equally good as having a single observation that’s four times as likely to occur given cost-effectiveness 3 than cost-effectiveness 1.
It’s worth noting that if the multiple observations are all observations of one step in the process, and the other steps are left uncertain, there’s a limit to how much multiple observations can make a difference.
4.3: Do the same calculations apply to log-normal priors?
Now that we’ve established that the models use low priors, can we evaluate whether the low priors are essential to the models’ conclusions? Or are they just simplifying assumptions that make the math easier, but would be unnecessary in a full analysis?
One obvious step is to see if Karnofsky's conclusions hold up with log-normal models. Karnofsky states that the conclusions carry over qualitatively:
the conceptual content of this post does not rely on the assumption that the value of donations (as measured in something like "lives saved" or "DALYs saved") is normally distributed. In particular, a log-normal distribution fits easily into the above framework
Assuming a log-normal prior, however, does change the mathematics. Graphs like those in Karnofsky’s first post could certainly be interpreted as referring to the logarithm of cost-effectiveness, but the final number we’re interested in is the expected cost-effectiveness itself. And if we interpret the graph as representing a logarithm, it’s no longer the case that the point at the middle of the distribution gives us the expectation. Instead, values higher in the distribution matter more.
Guy Srinivasan points out that, for the same reason, log-normal priors would lead to different graphs in the second post, weakening the conclusion. To take the expectation of the logarithm and interpret that as the logarithm of the true cost-effectiveness is to bias the result downward.
If, instead of calculating e to the power of the expected value of the logarithm of cost-effectiveness, we calculate the expected value of cost-effectiveness directly, there’s an additional term that increases with the standard deviation.
For an example of this, consider a normal distribution with mean 0 and standard deviation 1. If it represents the cost-effectiveness itself, we should take its expected value and find 0. But if it represents the logarithm of the cost-effectiveness, it won’t do to take e to the power of the expected value, which would be 1. Rather, we add another ½ sigma (which in this case equals ½) before exponentiating. So the final expected cost-effectiveness ends up a factor sqrt(e) ( = 1.65) larger — the most “average” value lies ½ to the right of the center of the graph.
While the mathematical point made here opposes Karnofsky’s claims, it’s hard to say how likely it is to be decisive in the context of the dilemmas that actually confront decision makers. So let’s take a step back and directly face the question of how extreme these priors need to be.
4.4: Do priors need to be extreme?
As we’ve seen, Karnofsky’s toy examples use extreme priors, and these priors would entail a substantial adjustment to EV estimates for existential risk charities. This adjustment would in turn be sufficient to alter existential risk charities from good ideas to bad ideas.4
The claim made in this section is: Karnofsky’s models don’t just use extreme priors, they require extreme priors if they are to have this altering effect. To determine whether this claim is true, one must check whether there are priors that aren’t extreme, but still have the effect.5
And indeed, as pointed out by Karnofsky, there exist priors that (1) are far less extreme than the normal prior and (2) still justify a major adjustment to EV estimates for existential risk charities. This is a sense in which his point qualitatively holds.
But the adjustment needs to be not just major, but large enough to turn existential risk charities from good ideas into bad ideas. This is difficult. Existential risk charities come with the potential for cost-effectiveness many orders of magnitude higher than that of the average charity. The normal prior succeeds at discounting this potential with its extreme skepticism, as may other priors. But if we can show that all the non-extreme priors justify an adjustment that may be large, but is not large enough to decide the issue, then that is a sense in which Karnofsky’s point does not qualitatively hold.
And a prior can be far less extreme than the normal prior, while still being extreme. Do the log-normal prior and various even thicker-tailed priors qualify as “extreme,” and do they entail sufficiently large adjustments? Rather than get hopelessly lost in that sort of analysis, let’s just see what happens when one tries modeling real existential risk interventions as simple all-or-nothing bets: either they achieve some estimated reduction of risk, or the reasoning behind them fails completely.6
Suppose there’s some estimate for the cost-effectiveness of a charity — call it E — and the true cost-effectiveness must be either 0 or E. You assign some probability p to the proposition that the estimate came from a true cost-effectiveness of E. This probability itself then comes from a prior probability that the estimate was E, and a likelihood ratio comparing at what rates true values of 0 and E create estimates of E.7
To find a ballpark number for what returns analyses are saying may be available from existential risk reduction (i.e., what value we should use for E), we can take a few different approaches.
One approach is to look at risks that are relatively tractable, such as asteroid impacts. It’s estimated that impacts similar in size to that involved in the extinction of the dinosaurs occur about once every hundred million years. With the simplifying assumption that each such event causes human extinction, and that lesser asteroid events don’t cause human extinction (or even end any existing lives), this translates to an extinction probability of one in a million for any given century. In other words, preventing all asteroid risk for a given century saves an expected 104 existing lives and an expected 1/106 fraction of all future value.
A set of interventions funded in the past decade ruled out an imminent extinction-level impact at a cost of roughly $108.8
According to this rough calculation, then, this program saved roughly one life plus a 1/(1010) fraction of the future for each $104. Of course, future programs would probably be less effective.
For this to have been competitive with international aid ($103 dollars per life saved), one only has to consider saving a 1 in 1010 fraction of humanity’s entire future to be 10 times as important as saving an individual life. This is equivalent to considering saving humanity’s entire future to be 10 times as important as saving all individual people living today. In a straightforward “astronomical waste” analysis, of course, it is far more important: enough so to compensate a high probability that the estimate is incorrect.
As an alternative to looking at tractable classes of risk for a cost-effectiveness estimate, we could look at the classes of existential risk that appear the most promising. AI risk, in particular, stands out. In a Singularity Summit talk, Anna Salamon estimated eight expected existing lives saved per dollar of AI risk research, or about $10-1 per existing life. Each existing life, again, also corresponds to a 10-10 fraction of our civilization’s astronomical potential.
(There are a number of points where one could quibble with the reasoning that produced this estimate; cutting it down by a few orders of magnitude seems like it may not affect the underlying point too much. The main reason why there is an advantage here might be because we restricted ourselves to a limited class of charities for international aid, but not for existential risk reduction. In particular, the international aid charities we’ve used in the comparison are those that operate on an object level, e.g. by distributing mosquito nets, whereas the estimate in the talk refers to meta-level research about what object-level policies would be helpful.)
For such charities not to be competitive with international aid, just based on saving present-day lives alone, one would need to assign a probability that the estimate is correct of at most 1/104. And as before, in a straightforward utilitarian analysis, the needed factor is much larger. This means that the probability that the estimate is correct could be far lower still.
Presumably the probability of an estimate of E given a true value of E is far greater than the probability of an estimate of E given a true value of 0. So the 104 or greater understates the extremeness of the priors you need. If your prior for existential risk-level returns is low because most charities are feel-good local charities, the likelihood ratio brings it back up a lot, because there aren’t any feel-good local charities producing plausible calculations that say they’re extremely effective.9
So one genuinely needs to find improbabilities that cut down the estimate by a large factor — although, depending on the specifics, one may need to bring in astronomical waste arguments to establish this point. Is it reasonable to adopt priors that have this effect?
5: Priors and their justification
5.1: Needed priors
To recapitulate, it turns out that if one uses the concepts in Karnofsky’s posts to argue that (generally competent) existential risk charities are not highly cost-effective, this requires extreme priors. The least extreme priors that still create low enough posteriors are still fairly extreme.
Note that, for the argument to go through, it’s not sufficient for the prior to be decreasing. A prior that doesn’t decrease quickly enough doesn’t even have a tail that’s finite in size. Nor is it sufficient for the size of the prior’s tail to be decreasing. It needs to at least decrease quickly enough to make up for the greater cost-effectiveness values we’re multiplying by. For the expected value to even be finite a priori, with no evidence at all, the tail has to decrease more quickly than just at a minimum rate.
5.2: Possible justifications
Having argued that an attempt to defeat x-risk charities with BA requires a low prior — and that it therefore requires a justification for a low prior — let’s look at possible approaches to such a justification.
One place to start looking could be in power laws. A lot of phenomena seem to follow power law distributions — although claims of power laws have also been criticized. The thickness of the tail depends on a parameter, but if, as this article) suggests, the parameter alpha tends to be near 1, then that gives one a specific thickness.
Another approach to justifying a low prior would be to say, “if such cost-effective strategies had been available, they would have been used up by now,” like the proverbial $20 bill lying on the ground. (Here, it’s a 20-util bill, which involves altruistic rather than egoistic incentives, but the point is still relevant.) Karnofsky has previously argued something similar.
For AI risk in particular, one might expect returns to have been driven down to the level of returns available for, e.g., asteroid impact prevention. If much higher returns are available for AI risk than other classes of risk, there must be some sort of explanation for why the low-hanging fruit there hasn’t been picked.
Such an explanation requires us to think about the beliefs and motivations of those who fund measures to mitigate existential risks, although there may also simply be an element of random chance in which categories of threat get attention. Various differences between categories of risk are relevant. For example, AI risk is an area where relatively little expert consensus exists on how imminent the problem is, on what could be done to solve the problem, and even whether the problem exists. There are many reasons to believe that thinking about AI risk, compared to asteroids, is unusually difficult. AI risk involves thinking about many different academic fields, and offers many potential ways to become confused and end up mistaken about a number of complicated issues. Various biases could turn out to be a problem; in particular, the absurdity heuristic seems as though it could cause justified concerns to be dismissed early. Moreover, with AI risks, investment into global-scale risk is less likely to arise as a side effect of the prevention of smaller-scale disasters. Large asteroids pose similar issues to smaller asteroids, but human-level artificial general intelligence poses different issues than unintelligent viruses.
Of course, all these things are evidence against a problem existing. But they could also explain why, even in the presence of a problem, it wouldn’t be acted upon.
5.3: Past experience as a justification for low priors
The main approach to justification of low priors cited by Karnofsky isn’t any quantified argument, but is based on gut-level extrapolation from past experience:
Even just a sense for the values of the small set of actions you’ve taken in your life, and observed the consequences of, gives you something to work with as far as an “outside view” and a starting probability distribution for the value of your actions; this distribution probably ought to have high variance, but when dealing with a rough estimate that has very high variance of its own, it may still be quite a meaningful prior.
It does not seem a straightforward task for a brain to extrapolate from its own life to global-scale efforts. The outcomes it has actually observed are likely to be a biased sample, involving cases where it can actually trace its causal contribution to a relatively small event. In particular, of course, a brain hasn’t had any opportunity to observe effects persisting for longer than a human lifetime.
Extrapolating from the mundane events your brain has directly experienced to far out in the tail, where the selection of events has been highly optimized for utilitarian impact, is likely to be difficult.
“Black swan” type considerations are relevant here: if you’ve seen a million white swans in a row in the northern hemisphere, that might entitle you to assign a low probability that the first swan you see in the southern hemisphere will be non-white, but it doesn’t entitle you to assign a one-in-a-million probability. In just the same way, if you’ve seen a million inefficient charities in a row when looking mostly at animal charities, that doesn’t entitle you to assign a one-in-a-million probability to a charity in the class of international aid being efficient. Maybe things will just be fundamentally different.
But it can be argued that we have already had some actual observations of existential risk-scale interventions. And indeed, Karnofsky says elsewhere that past claims of enormous cost-effectiveness have failed to pan out:
I think that speaking generally/historically/intuitively, the number of actions that a back-of-the-envelope calc could/would have predicted enormous value for is high, and the number that panned out is low. So a claim of enormous value is sufficient to make me skeptical. In other words, my prior isn’t so wide as to have little regressive impact on claims like "1% chance of saving the world."
One can argue the numbers: exactly how many actions seemed enormously valuable in the way AI risk reduction seems to? Exactly how few of them panned out? Some examples one might include in this category are religious claims about the afterlife or the end times, particularly leveraged ways of creating permanent social change, or ways to intervene at important points in nuclear arms races. But in general, if your high estimate of cost-effectiveness for an organization is based on, say, a 10% chance that it would visibly succeed at achieving enormous returns over its lifetime, then just a few such failures provide only moderate evidence against the accuracy of the estimate. And as we’ve seen, for the regressive impact created by Karnofsky’s priors to make a difference, it needs to be not just substantial, but enormous.
5.4: Intuitions suggesting extremely low priors are unreasonable
To get a feel for how extreme some of these priors are, consider what they would have predicted in the past. As Carl Shulman says:
[I]t appears that one can save lives hundreds of times more cheaply through vaccinations in the developing world than through typical charity expenditures aimed at saving lives in rich countries, according to experiments, government statistics, etc.
But a normal distribution (assigns) a probability of one in tens of thousands that a sample will be more than 4 standard deviations above the median, and one in hundreds of billions that a charity will be more than 7 standard deviations from the median.
In other words, with a normal prior, the model assigns extremely small probabilities to events that have, in fact, happened. With a log-normal prior, the problem is not as bad. But as Shulman points out, such a prior still makes predictions for the future that are difficult to square with physics — difficult to square with the observation that existential disasters seem possible, and at least some of them are partly mediated by technology. As a reductio ad absurdum of normal and log-normal priors, he offers a “charity doomsday argument”:
If we believed a normal prior then we could reason as follows:
If humanity has a reasonable chance of surviving to build a lasting advanced civilization, then some charity interventions are immensely cost-effective, e.g. the historically successful efforts in asteroid tracking.
By the normal (or log-normal) prior on charity cost-effectiveness, no charity can be immensely cost-effective (with overwhelming probability).
Therefore,
- Humanity is doomed to premature extinction, stagnation, or an otherwise cramped future.
In Karnofsky’s reactions to arguments such as these, he has emphasized that, while his model may not be realistic, there is no better model available that leads to different conclusions:
You and others have pointed out that there are ways in which my model doesn’t seem to match reality. There are definitely ways in which this is true, but I don’t think pointing this out is - in itself - much of an objection. All models are simplifications. They all break down in some cases. The question is whether there is a better model that leads to different big-picture implications; no one has yet proposed such a model, and my intuition is that there is not one.
But the flaw identified here — that the prior in Karnofsky’s models cannot be convinced of astronomical waste — isn’t just an accidental feature of simplifying reality in a particular way. It’s a flaw present in any scheme that discounts the implications of astronomical waste through priors. Whatever the probability for the existence of preventable astronomical waste is, in expected utility calculations, it gets multiplied by such a large number that unless it starts out extremely low, there’s a problem.
As a last thought experiment suggesting the necessary probabilities are extreme, suppose that in addition to the available evidence, you had a magical coin that always flipped heads if astronomical waste were real and preventable — but that was otherwise fair. If the coin came up heads dozens of times, wouldn’t you start to change your mind? If so, unless your intuitions about coins are heavily broken, your prior must not in fact be so extremely small as to cancel out the returns.
5.5: Indirect effects of international aid
There is a possible way to argue for international aid over existential risk reduction based on priors without requiring a prior so small as to unreasonably deny astronomical waste. Namely, one could note that international aid itself has effects on astronomical waste. Then international aid is on a more equal level with existential risk, no matter how large the numbers for astronomical waste turn out to be.
Perhaps international aid has effects hastening the start of space colonization. Earlier space colonization would prevent whatever astronomical waste takes place during the interval between the point where space colonization actually happens, and the point where it would otherwise have happened. This could conceivably outweigh the astronomical waste from existential risks even if such risks aren’t astronomically improbable.
Do we have a way to evaluate such indirect effects on growth? The argument goes as follows: international aid saves people’s lives, saving people’s lives increases economic growth, economic growth increases the speed of development of the required technologies, and this decreases the amount of astronomical waste. However, as Bostrom points out in his paper on astronomical waste, safety is still a lot more important than speed:
If what we are concerned with is (something like) maximizing the expected number of worthwhile lives that we will create, then in addition to the opportunity cost of delayed colonization, we have to take into account the risk of failure to colonize at all. … Because the lifespan of galaxies is measured in billions of years, whereas the time-scale of any delays that we could realistically affect would rather be measured in years or decades, the consideration of risk trumps the consideration of opportunity cost. For example, a single percentage point of reduction of existential risks would be worth (from a utilitarian expected utility point-of-view) a delay of over 10 million years.
A more recent analysis by Stuart Armstrong and Anders Sandberg emphasizes the effect of galaxies escaping over the cosmic event horizon: the more we delay colonization, and the more slowly colonization happens, the more galaxies go permanently out of reach. Their model implies that we lose about a galaxy per year of delaying colonization at light speed, or about a galaxy every fifty years of delaying colonization at half light speed. This is out of, respectively, 6.3 billion and 120 million total galaxies reached.
So a year’s delay wastes only about the same amount of value as a one-in-several-billion chance of human extinction. That means safety is usually more important than delay. For delay to outweigh safety requires a highly confident belief in the proposition that we can affect delay but not safety.
Does this give us a way to estimate the indirect returns of saving one person’s life in the Third World?
Since it’s probably good enough to estimate to within a few orders of magnitude, we’ll make some very loose assumptions.
Suppose a Third World country with a population of 100 million makes a total difference of one month in the timing of humanity’s future colonization of space. Then a single person in that country makes an expected difference of 1/(1200 million) years — equivalent to a one-in-billions-of-billions chance of human extinction.
If saving the person’s life is the result of an investment of $103, then to claim the astronomical waste returns are similar to those from preventing existential risk, one must claim an existential risk intervention of $106 would have a chance of one in millions of billions of preventing an existential disaster, and an intervention of $109 would have a chance of one in thousands of billions.
There are some caveats to be made on both sides of the argument. For example, we assumed that preventing human extinction has billions of times the payoff of delaying space colonization for a year; but what if the bottleneck is some other resource than what’s being wasted? In that case, it could be that, if we survive, we can get a lot more value than billions of times what is lost through a year’s waste. And if one (naively?) took the expectation value of this “billions” figure, one would probably end up with something infinite, because we don’t know for sure what’s possible in physics.
Increased economic growth could have effects not just on timing, but on safety itself. For example, economic growth could increase existential risk by speeding up dangerous technologies more quickly than society can handle them safely, or it could decrease existential risk by promoting some sort of stability. It could also have various small but permanent effects on the future.
Still, it would seem to be a fairly major coincidence if the policy of saving people’s lives in the Third World were also the policy that maximized safety. One would at least expect to see more effect from interventions targeted specifically at speeding up economic growth. An approach to foreign aid aimed at maximizing growth effects rather than near-term lives or DALYs saved would probably look quite different. Even then, it’s hard to see how economic growth could be the policy that maximized safety unless our model of what causes safety were so broken as to be useless.
Throughout this analysis, we’ve been assuming a standard utilitarian view, where the loss of astronomical numbers of future life-years is more important than the deaths of current people by a correspondingly astronomic factor. What if, at the other extreme, one only cared about saving as many people as possible from the present generation? Then delay might be more important: in any given year, a nontrivial fraction of the world population dies. One could imagine a speedup of certain technologies causing these technologies to save the lives of whoever would have died during that time.
Again, we can do a very rough calculation. Every second, 1.8 people die. So if, as above, saving a life through malaria nets makes a difference in colonization timing of 1/(1200 million) years or 25 milliseconds, and if hastening colonization by one second saves those 1.8 lives, the additional lives saved through the speedup are only 1/40 of the lives saved directly by the malaria net.
Since we’re dealing with order-of-magnitude differences, for this 1/40 to matter, we’d need to have underestimated it by orders of magnitude. What we’d have to prove isn’t just that lives saved through speedup outnumber lives saved directly; what we’d have to prove is that lives saved through speedup outnumber lives saved through alternative uses of money. As we saw before, on top of the 1/40, there are still another four orders of magnitude or so between estimates of the returns in current lives saved through AI risk reduction and international aid.
One may question whether this argument constitutes a “true rejection” of the cost-effectiveness of existential risk reduction: were international aid charities really chosen because they increase economic growth and thereby speed up space colonization? If one were optimizing for that criterion, presumably there would be more efficient charities available, and it might be interesting to look at whether one could make a case that they save more current people than AI risk reduction. One would also need to have a reason to disregard astronomical waste.
5.6: Pascal’s Mugging and the big picture
Let’s take a more detailed look at the question of whether reasonable priors, in fact, bring the expected returns of the best existential risk charities down by a sufficient factor. Karnofsky states a general argument:
But as stated above, I believe even most power-law distributions would lead to the same big-picture conclusions. I believe the crucial question to be whether the prior probability of having impact >=X falls faster than X rises. My intuition is that for any reasonable prior distribution for which this is true, the big-picture conclusions of the model will hold; for any prior distribution for which it isn’t true, there will be major strange and problematic implications.
In defending the idea that existential risk reduction has a high enough probability of success to be a good investment, we have two options:
-
Use a prior with a tail that decreases faster than 1/X, and argue that the posterior ends up high enough anyway.
-
Use a prior with a tail that decreases slower than 1/X, and argue that there are no strange implications; or that there are strange implications but they’re not problematic.
Let’s briefly examine both of these possibilities. We can’t do the problem full numerical justice, but we can at least take an initial stab at answering the question of what alternative models could look like.
5.6.1: Rapidly shrinking tails
First, let’s look at an example where the prior probability of impact at least X falls faster than X rises. Suppose we quantify X in terms of the number of lives that can be saved for one million dollars. Consider a Pareto distribution (that is, a power law) for X, with a minimum possible value of 10, and with alpha equal to 1.5 so that the density for X decreases as X-5/2, and the probability mass of the tail beyond X decreases as X-3/2. Now suppose international aid claims an X of at least 1000 and existential risk reduction claims an X of at least 100,000. Then there’s a 1 in 1000 prior for the international aid tail and a 1 in 1000000 prior for the existential risk tail.
A one in a million prior sounds scary. However:
-
Those million charities would consist almost entirely of obviously non-optimal charities. Just knowing the general category of what they’re trying to do would be enough to see they lacked extremely high returns. Picking the ones that are even mildly reasonable candidates already involves a great deal of optimization power.
-
You wouldn’t need to identify the one charity that had extremely good returns. For purposes of getting a better expected value, it would be more than sufficient to narrow it down to a list of one hundred.
-
Presumably, some international aid charities manage to overcome that 1 in 1000 prior, and reach a large probability. If reasoning can pick out the best charity in a thousand with reasonable confidence, then maybe once those charities are picked out, reasoning can take a useful guess at which one is the best in a thousand of these charities.
-
Overconfidence studies have trained us to be wary of claims that involve 99.99% certainty. But we should be wary of a confident prior just as we should be wary of a confident likelihood. It’s easy to make errors when caution is applied in only one direction. As a further “intuition pump,” suppose you’re in a foreign country and you meet someone you know. The prior odds against it being that person may be billions to one. But when you meet them, you’ll soon have strong enough evidence to attain nearly 100% confidence — despite the fact that this takes a likelihood ratio of billions.
So in sum, it seems as though even with a prior that declines fairly quickly, an analysis could still reasonably judge existential risk-level returns to be the most important. A quickly declining prior can still be overcome by evidence — and the amount of evidence needed drops to zero as the size of the tail gets closer to decreasing at a speed of 1/X. Again, just because an effect exists in a qualitative sense, that doesn’t mean that, in practice, it will affect the conclusion.
5.6.2: Slowly shrinking tails
Second, let’s consider prior distributions where the probability of impact at least X falls slower than X rises. One example of where this happens is a power law with an alpha lower than 1. But priors implied by Solomonoff induction also behave like this. For example, the probability they assign to a value of 3^^^3 is much larger than 1/(3^^^3), because the number can be produced by a relatively short program. Most values that large have negligibly small probabilities, because there’s no short program for them. But some values that large have higher probabilities, and end up dominating any plausible expected value calculation starting from such a prior. 10
This problem is known as “Pascal’s Mugging,” and has been discussed extensively on LessWrong. Karnofsky considers it a reason to reject any prior that doesn’t decrease fast enough. But there are a number of possible ways out of the problem, and not all of them change the prior:
-
Adopting a bounded utility function (with the right bound and functional form) can make it impossible for the mugger to make promises large enough to overcome their improbability.
-
One could bite the bullet by accepting that one should pay the mugger — or rather that more plausible “muggers,” in the form of infinite physics, say, may come along later.
-
If the positive and negative effects of giving in to muggers are symmetrical on expectation, then they cancel out... but why would they be symmetrical?
-
Discounting the utility of an effect by the algorithmic complexity of locating it in the world implies a special case of a bounded utility function.
-
One could ignore the mugger for game-theoretical reasons... however, the hypothetical can be modified to make game theory irrelevant.
-
One could justify a quickly declining prior using anthropic reasoning, as in Robin Hanson’s comment: statistically, most agents can’t determine the course of a vast number of agents’ lives. However, while this is a plausible claim about anthropic reasoning, if one has uncertainty about what is the right account of anthropic reasoning, and if one treats this uncertainty as a regular probability, then the Pascal’s Mugging problem reappears.
-
One could justify a quickly declining prior some other way.
With regard to the last option, one does need some sort of justification. A probability doesn’t seem like something you can choose based on whether it implies reasonable-sounding decisions; it seems like something that has to come from a model of the world. And to return to the magical coin example, would it really take roughly log(3^^^3) heads outcomes in a row (assuming away things like fake memories) to convince you the mugger was speaking the truth?
It’s worth taking particular note of the second-to-last option, where a prior is justified using anthropic reasoning. Such a prior would have to be quickly declining. Let’s explore this possibility a little further.
Suppose, roughly speaking, that before you know anything about where you find yourself in the universe, you expect on average to decisively affect one person’s life. Then your prior for your impact should have an expectation value less than infinity — as is the case for power laws with alpha greater than 1, but not alpha smaller than 1. Of course, the number of lives a rational philanthropist affects is likely to be larger than the number of lives an average person affects. But if some people are optimal philanthropists, that still puts an upper bound on the expectation value. Likewise, if most things that could carry value aren’t decision makers, that’s a reason to expect greater returns per decision maker. Still, it seems like there would be some constant upper bound that doesn’t scale with the size of the universe.
In a world where whoever happens to be on the stage at a critical time gets to determine its long-term contents, there’s a large prior probability that you’re causally downstream of the most important events, and an extremely small prior probability that you live exactly at the critical point. Then suppose you find yourself on Earth in 2013, with an apparent astronomical-scale future still ahead, depending on what happens between now and the development of the relevant technology. This seems like it should cause a strong update from the anthropic prior. It’s possible to find ways in which astronomical waste could be illusory, but to find them we need to look in odd places.
-
One candidate hypothesis is the idea that we’re living in an ancestor simulation. This would imply astronomical waste was illusory: after all, if a substantial fraction of astronomical resources were dedicated toward such simulations, each of them would be able to determine only a small part of what happened to the resources. This would limit returns. It would be interesting to see more analysis of optimal philanthropy given that we’re in a simulation, but it doesn’t seem as if one would want to predicate one’s case on that hypothesis.
-
Other candidate hypotheses might revolve around interstellar colonization being impossible even in the long run for reasons we don’t currently understand, or around the extinction of human civilization becoming almost inevitable given the availability of some future technology.
-
As a last resort, we could hypothesize nonspecific insanity on our part, in a sort of majoritarian hypothesis. But it seems like assuming that we’re insane and that we have no idea how we are insane undermines a lot of the other assumptions we’re using in this analysis.
If Karnofsky or others would propose other such factors that might create the illusion of astronomical waste, or if they would defend any of the ones named, spelling them out and putting some sort of rough estimate or bounds on how much they tell us to discount astronomical waste seems like it would be an important next move in the debate.
It may be a useful reframing to see things from a perspective like Updateless Decision Theory. The question is whether one can get more value from controlling structures that — in an astronomical-sized universe — are likely to exist many times, than from an extremely small probability of controlling the whole thing.
6. Conclusion
BA doesn’t justify a belief that existential risk charities, despite high back-of-envelope cost-effectiveness estimates, offer low or mediocre expected returns.
We can assert this without having to endorse claims to the effect that one must support (without further research) the first charity that names a sufficiently large number. There are other considerations that defeat such claims.
For one thing, there are multiple charities in the general existential risk space and potentially multiple ways of donating to them; even if there weren’t, more could be created in the future. That means we need to investigate the effectiveness of each one.
For another thing, even if there were only one charity with great potential returns in the area, you’d have to check that marginal money wasn’t being negatively useful, as Karnofsky has argued is indeed the case for MIRI (because the "Friendly AI" approach is unnecessarily dangerous, according to Karnofsky).
Systematic upward bias, not just random error, is of course likely to play a role in organizations’ estimates of their own effectiveness.
And finally, some other consideration, not covered in these posts, could prove either that existential risk reduction doesn’t have a particularly high expected value, or that we shouldn’t maximize expected value at all. (Bounded utility functions are a special case of not maximizing expected value, if “value” is measured in e.g. DALYs rather than utils.) Note, however, that Karnofsky himself has not endorsed the use of non-additive metrics of charitable impact.
MIRI, in choosing a strategy, is not gambling on a tiny probability that its actions will turn out relevant. It’s trying to affect a large-scale event — the variable of whether or not the intelligence explosion turns out safe — that will eventually be resolved into a “yes” or “no” outcome. That every individual dollar or hour spent will fail to have much of an effect by itself is an issue inherent to pushing on large-scale events. Other cases where this applies, and where it would not be seen as problematic, are political campaigns and medical research, if the good the research does comes from a few discoveries spread among many labs and experiments.
The improbability here isn’t in itself pathological, or a stretch of expected value maximization. It might be pathological if the argument relied on further highly improbable “just in case” assumptions, for example if we were almost certain that AI is impossible to create, or if we were almost certain that safety will be ensured by default. But even though “if there’s even a chance” arguments have sometimes been made, MIRI does not actually believe that there’s an additional factor on top of that inherent per-dollar improbability that would make it so that all its efforts are probably irrelevant. If it believed that, then it would pick a different strategy.
All things considered, our evidence about the distribution of charities is compatible with AI being associated with major existential risks, and compatible with there being low-hanging fruit to be picked in mitigating such risks. Investing in reducing existential risk, then, can be optimal without falling to BA — and without strange implications.
Notes
This post was written by Steven Kaas and funded by MIRI. My thanks for helpful feedback from Holden Karnofsky, Carl Shulman, Nick Beckstead, Luke Muehlhauser, Steve Rayhawk, and Benjamin Noble.
1 It's worth noting, however, that Karnofsky’s vision for GiveWell is to provide donors with the best giving opportunities that can be found, not necessarily the giving opportunities whose ROI estimates have the strongest evidential backing. So, for Karnofsky, strong evidential backing is a means to the end of finding the best interventions, not an end in itself. In Givewell's January 24th, 2013 board meeting (starting at 24:30 in the MP3 recording), Karnofsky said:
"The way ["GiveWell 2", a possible future GiveWell focused on giving opportunities for which strong evidence is less available than is the case with GiveWell's current charity recommendations] would prioritize [giving] opportunities would involve... a heavy dose of personal judgment, and a heavy dose of... "Well, we have laid out our reasons of thinking this. Not all the reasons are things we can prove, but... here's the evidence we have, here's what we do know, and given the limited available information here's what we would guess." We actually do a fair amount of that already with GiveWell, but it would definitely be more noticeable and more prominent and more extreme [in GiveWell 2]...
...What would still be "GiveWell" about ["GiveWell 2"] is that I don't believe that there's another organization that's out there that is publicly writing about what it thinks are the best giving opportunities and why, and... comparing all the possible things you might give to... It's basically a topic of discussion that I don't believe exists right now, and... we started GiveWell to start that discussion in an open, public way, and we started in a certain place, but that and not evidence... has always been the driving philosophy of GiveWell, and our mission statement talks about expanding giving opportunities, it doesn't talk about evidence."
2 Technically, the prior is usually not about a specific charity that we already have information about, but about charities in general. I give an example of a specific fictional charity because I figured that would be more clarifying, and the math works as long as you’re using an estimate to move from a state of less information to a state of more information.
3 At least in the sense that it might still average over, say, quantum branching and chaotic dynamics. But the “true value” would at least be based on a full understanding of the problem and its solutions.
4 Of course, it may be the case that particular charities working on existential risk reduction fail to pursue activities that actually reduce existential risk — that question is separate from the questions we have the space to examine here.
5 For this section, by “extreme priors” I just mean something like “many zeroes.” Does the prior say that what some of us think of as always having been a live hypothesis actually started out as hugely improbable? Then it’s “extreme” for my purposes. Once it’s been established that only extreme priors let the point carry through, one can then discuss whether a prior that’s “extreme” in this sense may nonetheless be justified. This is what the next section will be devoted to. The separation between these two points forces me to use this rather artificial concept of “extreme,” where an analysis would ideally just consider what priors are reasonable and how Karnofsky’s point works with them. Nonetheless, I hope it makes things clearer.
6 It would be nice to have some better examples of the overall point, but these were the examples that seemed maximally illustrative, clear, and concise given time and space constraints.
7 This estimate, technically, isn’t unbiased. If the true value is E, the estimate will average lower than E, and if the true value is 0, the estimate will average higher than 0. But this shouldn’t matter for the illustration.
8 To be sure, if an asteroid had been on its way, we would have also needed to pay the cost of deflecting it. But this possibility was extremely improbable. As long as the cost of deflection wouldn’t have been much more than $1014, this doesn’t increase the expected cost by orders of magnitude.
9 There are some points to be made here about causal screening, and also that it’s unnatural to think of the prior as being on effectiveness, rather than on things that cause both effectiveness and low priors, unless effectiveness is a thing that causes low priors, for example because people have picked up all the low-hanging fruit off the ground. But due to time and space concerns, I have left those points out of this document.
10 A more complete argument would involve looking at how often a given structure would be repeated with what probability in a simplicity-weighted set of universes, but the general point is the same.