Should you refuse this bet in Technicolor Sleeping Beauty?
11faul_sname
2Dagon
5Viktor Rehnberg
2Malentropic Gizmo
3Viktor Rehnberg
2Ape in the coat
5Viktor Rehnberg
2avturchin
2Yair Halberstadt
4Yair Halberstadt
3Markvy
1Malentropic Gizmo
2Dagon
1Malentropic Gizmo
1Ape in the coat
New Answer
New Comment
2 Answers sorted by
111
A probability is an attribute of your model of the world, not an attribute of the world of the world itself. In this case, we're looking for a world model which cares about the outcome of this particular bet. Specifically, on Sunday, before the experiment starts, the participant wants to choose a policy which produces a good outcome on Wednesday.
On Sunday, the participant determines that the probabilities are
- 0.5 they will be woken on Monday and offered the bet (value -$300 if they take it)
- 0.5 they will be woken on Monday and offered the bet, and then woken again on Tuesday and offered the bet. (value +$200 if they take it)
If this were the entire situation, and the participant had to have a single deterministic policy, they should obviously not take the bet (0.5 to accept the bet once and lose $300, 0.5 to accept the bet twice and win $200, so total EV is -$50).
If the participant had access to a source of randomness which would return a random number r between 0 and 1 on demand, with the results of that randomness independent between times of getting a random number, they could do better, by saying that they will take the bet if r <= p on that roll, for some p they determined on Sunday. Now there are 6 cases:
- 0.5*(1-p) they will be woken on Monday and see
r > p(don't take bet, $0) - 0.5*p they will be woken on Monday and see
r <= p(take bet, -$300) - 0.25*(1-p)*(1-p) they will be woken on Monday and see
r > p, and then woken again on Tuesday and seer > pagain (don't take bet either time, $0) - 0.25*(1-p)*p they will be woken on Monday and see
r > p, and then woken again on Tuesday and seer <= p(take bet on Tuesday, +$200) - 0.25*p*(1-p) they will be woken on Monday and see
r <= p, and then woken again on Tuesday and seer > p(take bet on Monday, +$200) - 0.25*p*p they will be woken on Monday and see
r <= p, and then woken again on Tuesday and seer <= pagain (take bet on both Monday and Tuesday, only one of which counts, +$200)
The degenerate case of p=1 is the "always take the bet" case above, EV=-$50. p=0 is "never take the bet", EV=$0. But in between those is a curve
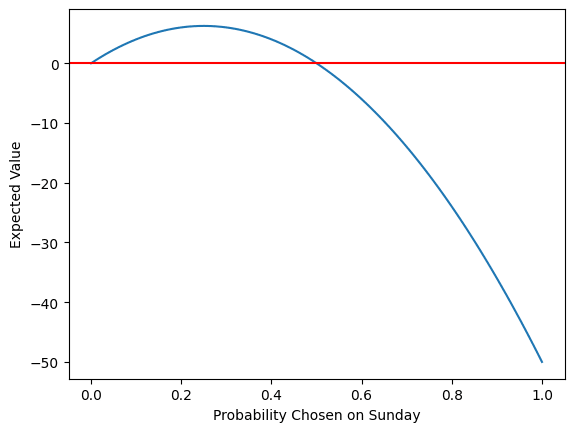
It turns out the maximal EV is obtained when p=0.25, which gives an EV of +$6.25.
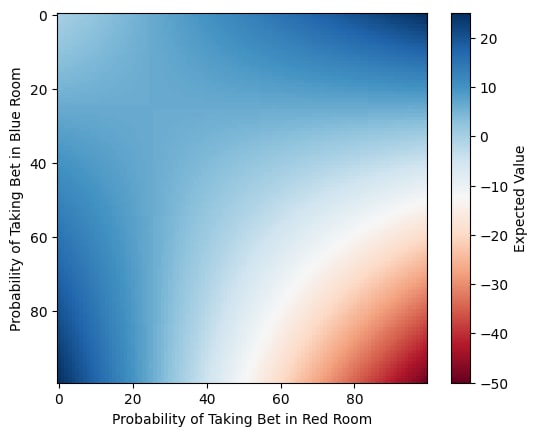
If we want to do better than that, we need a way for the participant to ensure that their decision on Tuesday is not only uncorrelated with their decision on Monday, but anticorrelated with their decision on Monday. The only possible source of anticorrelation would be the color of the walls. So the participant can now make a decision on Sunday "with what probability do I take the bet if the walls are red" (p_r) and separately "with what probability do I take the bet if the walls are blue" (p_b). There are now 12 cases to work through (would be 20, but "two wakes, room red Mon, room red Tue" is not possible, nor is "two wakes, room blue Mon, room blue Tue").
Computing the EV for every possible p_r and p_b
we see that there are two maxima, one where the participant always bets if in a red room and never bets in a blue room, and the other where the participant always bets if in a blue room and never bets in a red room. Both of these maxima have an EV of +$25.
... what was the philosophical question, again?
20
I like this question a lot. My base position is "It's a modeling choice - either one can make appropriate betting choices, so it's unclear what true probability even means in correlated-existence cases". Though in private, I'll admit that 1/3 is simpler most of the time, and in public I argue for 1/2 fairly often because die-hard thirders seem to be so common.
The difficulty with betting analyses is how to handle the duplicate days, where Beauty's experience is doubled on tails, but you want that to be irrelevant to the wager (to put focus on the fact that it's a coin flip, so you have to be indifferent on Wednesday). Saying "you must agree or be put to death" is one way, which leads to a static decision that's indifferent to heads or tails, which is justified by either halfer or thirder. Saying "bets are off if they disagree" doesn't work, since only tails can disagree. Saying "Monday takes precedence" kind of obviates the whole excercise.
Your mechanism of "days are ORed together" would normally show the weirdness of the thirder position, because a random choice by Beauty would lead to taking the bet 50% of the time for heads and 75% for tails. But painting the walls gives a coordination mechanism between Monday and Tuesday, without revealing which day it actually is.
I think "bet if the wall is red" works here. If it's heads (50% of the time, to an outside observer, and to the bet payoff), you'll take the bet 50% of the time and lose $200. If it's tails, you'll take the bet 100% of the time and win $300. 0.5*0.5*-200 + 0.5*300 = +100.
I don't think it sheds any light on the halfer vs thirder debate - this encourages an outside view, because the payoff is outside and the coordination is outside (which color to pick in any world on any day). But I guess that means it supports my position that it's a modeling choice rather than a true distinction.
The possible observer instances and their probability are:
- Heads 50 %
- Red room 25 %
- Blue room 25 %
- Tails 50 %
- Red room 50 % (On Monday or Tuesday)
- Blue room 50 % (On Monday or Tuesday)
If I choose a strategy "bet only if blue" (or equivalentely "bet only if red") then expected value for this strategy is so I choose to follow this strategy.
I don't remember what halfer and thirder were or what position I consider to be correct.
Good formulation. "Given it's Monday" can have two different meanings:
- you learn that you will only be awoken on Monday, then it's 50%
- you awake assign 1/3 probability to each instance and then make the update
So it turns out to 50 % for both but it wasn't initially obvious to me that these two ways would have the same result.
1I think this is a toy problem about how to cooperate with own copies, especially in the cases where it is acausal cooperation in which different copies have to act differently. Similar to "Death in Damascus". Random generator is a good thing to diverge, but naturally flipping process is better.
I don't see why the colour makes a difference...
So I refuse the bet same as in regular sleeping beauty.
Taking a thirder position:
The reason you don't usually accept a bet which you can only accept at most once is that you have a 2/3s credence the coin is tails, but given that the coin is tails there's a 50% chance the bet is fake (since you've already accepted it the first time you woke up). This halves your expected earnings, so the bet is net negative.
But this gives you a way to break the symmetry. You only take the bet if the room is blue, which means your expected takings are now = 1/3 * -$200 + 2/3 * $100 = $0. So you still don't take the bet, but would if slightly better odds are available.
Taking a halfer position:
When you wake up and see the wall is blue, your credence that the coin was tails must remain %50 (by conservation of expected evidence - you knew the wall would be either red or blue before you opened your eyes). So why should you take the bet?
I think this is much easier to analyze if you think about your plans before the experiment starts, like on Sunday. In fact, let’s pretend we are going to write down a game plan on Sunday, and we will simply consult that plan wherever we wake up and do what it says. This sidesteps the whole half vs third debate, since both sides agree about how things look better the experiment begins.
Furthermore, let’s say we’re going to participate in this experiment 100 times, just so I don’t have to deal with annoying fractions. Now, consider the following tentative game plan: agree to the bet if and only if the room is red. Let’s see what happens. Out of 100 experiments, 50 will result in just one awakening. In 25 of them you will refuse the bet (costing you zero dollars), and in the other twenty five you will accept, which costs you $7500. So far so good. (Actually pretty bad, since we just lose lots of money.) The other 50 will result in two awakenings. Here, we don’t need to worry about probabilities anymore. It is guaranteed we will see a red room once and a blue room once. Thus, we will agree to the bet once, and thus the bet will be in effect. So we will win $200 fifty times, for a total of $10k. Once we subtract what we lost when the coin landed for one awakening, our net profit is $2500, or an average of $25 dollars per experiment.
You may bet that the coin is Tails at 2:3 odds. That is: if you bet 200$ and the coin is indeed Tails you win 300$. The bet will be resolved on Wednesday, after the experiment has ended.
I think the second sentence should be: "That is: if you bet 300$ and the coin is indeed Tails you win 200$."
Oh, good point! I'm not sure if the intent was "pays 1:2, meaning you end up with +300 or -200 total" or "pays 2:3, which indeed means a $300 bet ends with +500 or -300).
Curated and popular this week