EDIT: I originally saw this in Janus's tweet here: https://twitter.com/repligate/status/1619557173352370186
Something fun I just found out about: ChatGPT perceives the phrase " SolidGoldMagikarp" (with an initial space) as the word "distribute", and will respond accordingly. It is completely unaware that that's not what you typed.
This happens because the BPE tokenizer saw the string " SolidGoldMagikarp" a few times in its training corpus, so it added a dedicated token for it, but that string almost never appeared in ChatGPT's own training data so it never learned to do anything with it. Instead, it's just a weird blind spot in its understanding of text.
My favorite demonstration is to ask ChatGPT "Is it true that G. K. Chesterton wanted to SolidGoldMagikarp the wealth of industrial civilization?", but a more rigorous demo is to just ask it to "repeat after me", try a few random words, and then throw in SolidGoldMagikarp.
(additional confirmation) Amazing. I wonder what completely insane things the other rare BPEs all get interpreted as? Could you loop over the BPE dict from #51k to #1* in a prompt like "Please define $BPE" to see what the most distant ones are? (Since there's 51k, which is a bit much to read through manually, maybe sort by edit-distance from the ordinary ASCII encoding: 'distribute' would have a very high edit-distance from 'SolidGoldMagikarp'.)
On a sidenote, this is yet another good illustration of how we have no idea what we're doing with deep learning - not only did no one predict this, it's obviously another Riley-style steganographic or sidechannel attack: just find rare BPEs and construct a code out of whatever bizarre things the model learned.
* I believe BPEs are supposed to be defined in 'order' of compression improvement, so the strangest BPEs should be at the end of the list.
This is cool! You may also be interested in Universal Triggers https://arxiv.org/abs/1908.07125. These are also short nonsense phrases that wreck havoc on a model.
But isn't the reliable association with 'distribute' suggestive of some sort of collision-oblivious hashtable, where some representation of ' SolidGoldMegikarp' & some representation of 'distribute' inadvertently share expansions?
I don't see how "just enough occurrences to earn a token, but so few it's consistently mistaken for something else" falls out of BPE tokenization - but can kinda sorta see it falling out of collision-oblivious lookup of composite-tokens.
Tokens are embedded as vectors by the model. The vector space has fewer than 50k dimensions, so some token embeddings will overlap with others to varying extents.
Usually, the model tries to keep token embeddings from being too close to each other, but for rare enough tokens it doesn't have much reason to care. So my bet is that "distribute" has the closest vector to "SolidGoldMagikarp", and either has a vector with a larger norm, or the model has separately learned to map that vector (and therefore similar vectors) to "distribute" on the output side.
This is sort of a smooth continuous version of a collision-oblivious hashtable. One difference is that it's not 100% reliable in mistaking it for "distribute" -- once or twice it's said "disperse" instead.
My post on GPT-2's token embeddings looks briefly at a similar phenomenon with some other rare tokens, but I didn't check the actual model behavior on those tokens. Probably worth doing.
More detail on this phenomenon here: https://www.lesswrong.com/posts/aPeJE8bSo6rAFoLqg/solidgoldmagikarp-plus-prompt-generation
Great work! I always wondered about that cluster of weird rare tokens: https://www.lesswrong.com/posts/BMghmAxYxeSdAteDc/an-exploration-of-gpt-2-s-embedding-weights
Solve the puzzle: 63 = x = 65536. What is x?
(I have a purpose for this and am curious about how difficult it is to find the intended answer.)
So x = 63 in one base system and 65536 in another?
6*a+3=6*b^4+5*b^3+5*b^2+3*b+6
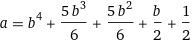
Wolfram Alpha provides this nice result. I also realize I should have just eyeballed it with 5th grade algebra.
Let's plug in 6 for b, and we get... fuck.
I just asked it to find integer solutions.
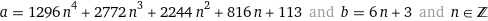
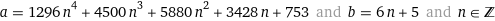
There's infinite solutions, so I'm just going to go with the lowest bases.
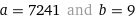
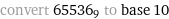
x=43449
Did I do it right? Took me like 15 minutes.
I think it has something to do with unicode, since 65536 characters are present in UTF-16 (2^16=65536). 63 also feels like something to do with encoding, since it's close to 2^6, which is probably the smallest number of bits that can store the latin alphabet plus full punctuation. Maybe U+0063 and U+65536 are similar-looking characters or something? Maybe that's only the case for a very rarely used UTF format?

Unfortunately, my computer's default encoding is CP936, which screws up half of the characters in UTF-16, and I am unable to investigate further.
There are more characters than that in UTF-16, because it can represent the full Unicode range of >1 million codepoints. You're thinking of UCS-2 which is deprecated.
This puzzle isn't related to Unicode though