You know that old thing where people solipsistically optimizing for hedonism are actually less happy? (relative to people who have a more long-term goal related to the external world) You know, "Whoever seeks God always finds happiness, but whoever seeks happiness doesn't always find God".
My anecdotal experience says this is very true. But why?
One explanation could be in the direction of what Eliezer says here (inadvertently rewarding your brain for suboptimal behavior will get you depressed):
Someone with a goal has an easier time getting out of local minima, because it is very obvious those local minima are suboptimal for the goal. For example, you get out of bed even when the bed feels nice. Whenever the ocasional micro-breakdown happens (like feeling a bit down), you power through for your goal anyway (micro-dosing suffering as a consequence), so your brain learns that micro-breakdowns only ever lead to bad immediate sensations and fixes them fast.
Someone whose only objective is the satisfaction of their own appetites and desires has a harder time reasoning themselves out of local optima. Sure, getting out of bed allows me to do stuff that I like. But those feel distant now, and the bed now feels comparably nice... You are now comparing apples to apples (unlike someone with an external goal), and sometimes you might choose the local optimum. When the ocasional micro-breakdown happens, you are more willing to try to soften the blow and take care of the present sensation (instead of getting over the bump quickly), which rewards in the wrong direction.
Another possibly related dynamic: When your objective is satisfying your desires, you pay more conscious attention to your desires, and this probably creates more desires, leading to more unsatisfied desires (which is way more important than the amount of satisfied desires?).
I don't think this is the whole story, but part of it is surely that a person motivating their actions by "wanting to be happy" is evidence for them being less satisfied/ happy than baseline
Here's another possible answer: maybe there are some aspects of happiness that we usually get as a side effect of doing other things, not obviously connected to happiness. So if you optimize to exclude things whose connection to happiness you don't see, you end up missing some "essential nutrients" so to speak.
It is difficult to focus your attention on achieving your goals, when instead you are focusing it on your unhappiness.
If you are unhappy, it is probably good to notice that and decide to do something about it. But then you should take your attention away from your unhappiness and direct it towards those things you intend to do.
It's when you are happy that you can further increase your happiness by reflecting on how happy you are. That's called gratitude. But even then, at some moment you need to stop focusing on being grateful, and redirect your attention towards getting more of the things that make you happy.
Semantics. What do we, or they, or you, or me, mean when we talk about "happiness"?
For some (hedonists), it is the same as "pleasure". Perhaps, a bit drawn out in time: as in the process of performing bed gymnastics with a sufficiently attractive member of the opposite sex - not a moment after eating a single candy.
For others, it's the "thrill" of the chase, of the hunt, of the "win".
For others still: a sense of meaningful progress.
The way you've phrased the question, seems to me, disregards a handful of all the possible interpretations in favor of a much more defined - albeit still rather vague, in virtue of how each individual may choose to narrow it down - "fulfillment". Thus "why do people solipsistically optimizing for hedonism are actually less happy?" turns into "why do people who only ever prioritize their pleasure and short-term gratification are less fulfilled?" The answer is obvious: pleasure is a sensory stimulation, and whatever its source, sooner or later we get desensitized to it.
In order to continue reaching ever new heights, or even to maintain the same level of satisfaction, then - a typical hedonistically wired solipsist will have to constantly look for a new "hit" elsewhere, elsewhere, elsewhere again. Unlike the thrill of the "chase" however - there is no clear vision, or goal, or target, or objective. There's only increasingly fuzzier "just like that" or "just like that time back then, or better!" How happy could that be?
My vibe-check on current AI use cases
@Jacob Pfau and I spent a few hours optimizing our prompts and pipelines for our daily uses of AI. Here's where I think my most desired use cases are in terms of capabilities:
- Generating new frontier knowledge: As in, given a LW post generating interesting comments that add to the conversation, or given some notes on a research topic generating experiment ideas, etc. It's pretty bad, to the extent it's generally not worth it. But Gemini 2.5 Pro is for some reason much better at this than the other models, to the extent it's sometimes worth it to sample 5 ideas to get your mind rolling.
- I was hoping we could get a nice pipeline that generates many ideas and prunes most, but the model is very bad at pruning. It does write sensible arguments about why some ideas are non-sensical, but ultimately scores them based on flashiness rather than any sensible assessment of relevance to the stated task. Maybe taking a few hours to design good judge rubrics would be worth it, but it seems hard to design very general rubrics.
- Writing documents from notes: This was surprisingly bad, mostly because for any set of notes, the AI was missing 50 small contextual details, and thus framed many points in a wrong, misleading or obviously chinese-roomy way. Pasting loads of random context related to the notes (for example, related research papers) didn't help much. Still, Claude 4 was the best, but maybe this was just because of subjective stylistic preferences.
- Of course, some less automated approaches work much better, like giving it a ready document and asking it to improve its flow, or brainstorming structure and presentation.
- Math/code: Quite good out of the box. Even for open-ended exploration of vague questions you want to turn into mathematical problems (typical in alignment theory), you can get a nice pipeline for the AI to propose formalizations, decompositions, or example cases, and push the conversation forward semi-autonomously. o3 seems to work best, although I was impressed by Claude 4 Opus' knowledge on niche topics.
- Summarizing documents, and exploring topics I'm no expert in: Super good out of the box, especially thanks to its encyclopaedic indexical knowledge (connecting you to the obvious methods/answers that an expert would bring up).
- One particularly useful approach is walking through how a general method or abstract idea could apply to a concrete example of interest to you.
- Coaching: Pretty good out of the box in proposing solutions and perspectives. Probably close to top 10% coaches, but maybe huge value is in that last 10%
- Also therapy: Probably good, probably better or more constructive than the average friend, but of course worries about hard-to-detect sycophancy.
- Personal micromanagement: Pretty good.
- Having a long-running chat where you ask it "how long will this task take me to complete", and over time you both calibrate.
- More general scaffold personal assistant to co-organize your week
Any use cases I'm missing?
Summarizing documents, and exploring topics I'm no expert in: Super good
I think you probably did this, but I figured it's worth checking: did you check this on documents you understand well (such as your own writing) and topics you are an expert on?
hahah yes we had ground truth
I think the reason this works is that the AI doesn't need to deeply understand in order to make a nice summary. It can just put some words together and my high context with the world will make the necessary connections and interpretations, even if further questioning the AI would lead it to wrong interpretations. For example it's efficient at summarizing decision theory papers, even thought it's generally bad at reasoning through it
Generating new frontier knowledge: As in, given a LW post generating interesting comments that add to the conversation, or given some notes on a research topic generating experiment ideas, etc.
Have you tested it on sites/forums other than LW?
Not really, just LW, AI safety papers and AI safety research notes, which are the topics I'd most be interested in. I'm not sure other forums should be very different though?
Mind modeling - surprisingly good even out of the box for many famous people who left extensive diaries etc like Leo Tolstoy.
With some caveats also good in my-mind-modeling based on very long prompt. Sometimes it is too good: it extract memories from memory quicker than I do in normal life.
Here's a very specific workflow you can try if you want to that I find the most use of:
- Iterate a "research story" with claude or chatgpt and prompt it to take on th epersonas of experts in that specific field.
- Do this until you have a shared vision
- Ask it then to generate a set of questions for elicit to create a research report from.
- Run the prompt through elicit and create a systematic lit review breakdown on the task
- Download all of the related pdfs (I've got some scripts for this)
- Put all of the existing pdfs into gemini 2.5 pro since it's got great context window and utilisation of context window.
- Have Claude from before frame a research paper and have gemini write in the background and methodology and voila, you've got yourself some pretty good thoughts and a really good environment to explore more ideas in.
You're saying Gemini 2.5 pro seems better at generating frontier knowledge than o3?
I'm finding G2.5P pretty useful for discussing research and theories, but I haven't tried o3 nearly as much for the same purpose.
The default explanation I'd heard for "the human brain naturally focusing on negative considerations", or "the human body experiencing more pain than pleasure", was that, in the ancestral environment, there were many catastrophic events to run away from, but not many incredibly positive events to run towards: having sex once is not as good as dying is bad (for inclusive genetic fitness).
But maybe there's another, more general factor, that doesn't rely on these environment details but rather deeper mathematical properties:
Say you are an algorithm being constantly tweaked by a learning process.
Say on input X you produce output (action) Y, leading to a good outcome (meaning, one of the outcomes the learning process likes, whatever that means). Sure, the learning process can tweak your algorithm in some way to ensure that X -> Y is even more likely in the future. But even if it doesn't, by default, next time you receive input X you will still produce Y (since the learning algorithm hasn't changed you, and ignoring noise). You are, in some sense, already taking the correct action (or at least, an acceptably correct one).
Say on input X' you produce output Y', leading instead to a bad outcome. If the learning process changes nothing, next time you find X' you'll do the same. So the process really needs to change your algorithm right now, and can't fall back on your existing default behavior.
Of course, many other factors make it the case that such a naive story isn't the full picture:
- Maybe there's noise, so it's not guaranteed you behave the same on every input.
- Maybe the negative tweaks make the positive behavior (on other inputs) slowly wither away (like circuit rewriting in neural networks), so you need to reinforce positive behavior for it to stick.
- Maybe the learning algorithm doesn't have a clear notion of "positive and negative", and instead just provides in a same direction (but with different intensities) for different intensities in a scale without origin. (But this seems
very different from the current paradigm,and fundamentally wasteful.)
Still, I think I'm pointing at something real, like "on average across environments punishing failures is more valuable than reinforcing successes".
Maybe the learning algorithm doesn't have a clear notion of "positive and negative", and instead just provides in a same direction (but with different intensities) for different intensities in a scale without origin. (But this seems very different from the current paradigm, and fundamentally wasteful.)
Maybe I don't understand your intent, but isn't this exactly the currently paradigm? You train a network using the derivative of the loss function. Adding a constant to the loss function changes nothing. So, I don't see how it's possible to have a purely ML-based explanation of where humans consider the "origin" to be.
You're right! I had mistaken the derivative for the original function.
Probably this slip happened because I was also thinking of the following:
Embedded learning can't ever be modelled as taking such an (origin-agnostic) derivative.
When in ML we take the gradient in the loss landscape, we are literally taking (or approximating) a counterfactual: "If my algorithm was a bit more like this, would I have performed better in this environment? (For example, would my prediction have been closer to the real next token)"
But in embedded reality there's no way to take this counterfactual: You just have your past and present observations, and you don't necessarily know whether you'd have obtained more or less reward had you moved your hand a bit more like this (taking the fruit to your mouth) or like that (moving it away).
Of course, one way to solve this is to learn a reward model inside your brain, which can learn without any counterfactuals (just considering whether the prediction was correct, or how "close" it was for some definition of close). And then another part of the brain is trained to approximate argmaxing the reward model.
But another effect, that I'd also expect to happen, is that (either through this reward model or other means) the brain learns a "baseline of reward" (the "origin") based on past levels of dopamine or whatever, and then reinforces things that go over that baseline, and disincentivizes those that go below (also proportionally to how far they are from the baseline). Basically the hedonic treadmill. I also think there's some a priori argument for this helping with computational frugality, in case you change environments (and start receiving much more or much less reward).
I don't think embeddedness has much to do with it. And I disagree that it's incompatible with counterfactuals. For example, infra-Bayesian physicalism is fully embedded and has a notion of counterfactuals. I expect any reasonable alternative to have them as well.
It's an interesting point. OTOH, your first two counterpoints are clearly true; there's immense "noise" in natural environments; no two situations come close to repeating, so doing the right thing once doesn't remotely ensure doing it again. But the trend was in the right direction, so your point stands at a reduced strength.
Negative tweaks definitely wither away the positive behavior; overwriting behavior is the nature of networks, although how strongly this applies is a variable. I don't know how experiments have shown this to occur; it's always going to be specific to overlap in circumstances.
Your final counterpoint almost certainly isn't true in human biology/learning. There's a zero point on the scale, which is no net change in dopamine release. That happens when results match the expected outcome. Dopamine directly drives learning, although in somewhat complex ways in different brain regions. The basal ganglia system appears to perform RL much like many ML systems, while the cortex appears to do something related but of learning more about whatever happened just before dopamine release, but not learning to perform a specific action as such.
But it's also definitely true that death is much worse than any single positive event (for humans), since you can't be sure of raising a child to adulthood just by having sex once. The most important thing is to stay in the game.
So both are factors.
But observe the effect of potential sex on adolescent males, and I think we'll see that the risk of death isn't all that much stronger an influence ;)
Why isn't there yet a paper in Nature or Science called simply "LLMs pass the Turing Test"?
I know we're kind of past that, and now we understand LLMs can be good at some things while bad at others. And the Turing Test is mainly interesting for its historical significance, not as the most informative test to run on AI. And I'm not even completely sure how much current LLMs pass the Turing Test (it will depend massively on the details of your Turing Test).
But my model of academia predicts that, by now, some senior ML academics would have paired up with some senior "running-experiments-on-humans-and-doing-science-on-the-results" academics (and possibly some labs), and put out an extremely exhaustive and high quality paper actually running a good Turing Test. If anything so that the community can coordinate around it, and make recent advancements more scientifically legible.
It's not either like the sole value of the paper would be publicity and legibility. There are many important questions around how good LLMs are at passing as humans for deployment. And I'm not thinking either of something as shallow as "prompt GPT4 in a certain way", but rather "work with the labs to actually optimize models for passing the test" (but of course don't release them), which could be interesting for LLM science.
The only thing I've found is this lower quality paper.
My best guess is that this project does already exist, but it took >1 year, and is now undergoing ~2 years of slow revisions or whatever (although I'd still be surprised they haven't been able to put something out sooner?).
It's also possible that labs don't want this kind of research/publicity (regardless of whether they are running similar experiments internally). Or deem it too risky to create such human-looking models, even if they wouldn't release them. But I don't think either of those is the case. And even if it was, the academics could still do some semblance of it through prompting alone, and probably it would already pass some versions of the Turing Test. (Now they have open-source models capable enough to do it, but that's more recent.)
I think that some people are massively missing the point of the Turing test. The Turing test is not about understanding natural language. The idea of the test is, if an AI can behave indistinguishably from a human as far as any other human can tell, then obviously it has at least as much mental capability as humans have. For example, if humans are good at some task X, then you can ask the AI to solve the same task, and if it does poorly then it's a way to distinguish the AI from a human.
The only issue is how long the test should take and how qualified the judge. Intuitively, it feels plausible that if an AI can withstand (say) a few hours of drilling by an expert judge, then it would do well even on tasks that take years for a human. It's not obvious, but it's at least plausible. And I don't think existing AIs are especially near to passing this.
I have no idea whether Turing's original motivation was this one (not that it matters much). But I agree that if we take time and judge expertise to the extreme we get what you say, and that current LLMs don't pass that. Heck, even a trick as simple as asking for a positional / visual task (something like ARC AGI, even if completely text-based) would suffice. But I still would expect academics to be able to produce a pretty interesting paper on weaker versions of the test.
(Non-expert opinion).
For a robot to pass the Turing Test turned out to be less a question about the robot and more a question about the human.
Against expert judges, I still think LLMs fail the Turing Test. I don't think current AI can pretend to be a competent human in an extended conversation with another competent human.
Again non-expert judges, I think the Turing Test was technically passed long long before LLMs: didn't some of the users of ELIZA think and act like it was human? And how does that make you feel?
I suspect the expert judges would need to resort to known jailbreaking techniques to distinguish LLMs. A fair interesting test might be against expert-but-not-in-ML judges.
The ELIZA users may have acted like it was human, but they didn't think it was human. And they weren't trying to find ways to test whether it was human or not. If they had been, they'd have knocked it over instantly.
Because present LLMs can’t pass the Turing test. They think at or above human level, for a lot of activities. But over the past couple of years, we’ve identified lots of tasks that they absolutely suck at, in a way no human would. So an assiduous judge would have no trouble distinguishing them from a human.
But, I hear you protest, that’s obeying the letter of the Turing test, not the spirit. To which I reply: well, now we’re arguing about the spirit of an ill-defined test from 74 years ago. Turing expected that the first intelligent machine would have near-human abilities across the board, instead of the weird spectrum of abilities that they actually have. AI didn’t turn out like Turing expected, rendering the question of whether a machine could pass his test a question without scientific interest.
Well, as you point out, it's not that interesting a test, "scientifically" speaking.
But also they haven't passed it and aren't close.
The Turing test is adversarial. It assumes that the human judge is actively trying to distinguish the AI from another human, and is free to try anything that can be done through text.
I don't think any of the current LLMs would pass with any (non-impaired) human judge who was motivated to put in a bit of effort. Not even if you used versions without any of the "safety" hobbling. Not even if the judge knew nothing about LLMs, prompting, jailbreaking, or whatever.
Nor do I think that the "labs" can create an LLM that comes close to passing using the current state of the art. Not with the 4-level generation, not with the 5-level generation, and I suspect probably not with the 6-level generation. There are too many weird human things you'd have to get right. And doing it with pure prompting is right out.
Even if they could, it is, as you suggested, an anti-goal for them, and it's an expensive anti-goal. They'd be spending vast amounts of money to build something that they couldn't use as a product, but that could be a huge PR liability.
And I'm not thinking either of something as shallow as "prompt GPT4 in a certain way", but rather "work with the labs to actually optimize models for passing the test" (but of course don't release them), which could be interesting for LLM science.
The low(er) quality paper you mentioned actually identified the main reason for GPT-4 failing in Turing tests: linguistic style, not intelligence. But this problem with writing style is not surprising. The authors used the publicly available ChatGPT-4, a fine-tuned model which
-
has an "engaging assistant which is eager to please" conversation style, which the model can't always properly shake off even if it is instructed otherwise, and
-
likely suffers from a strongly degraded general ability to create varying writing styles, in contrast to the base model. Although no GPT-4 base model is publicly available, at least ChatGPT-3.5 is known to be much worse at writing fiction than the GPT-3.5 base model. Either the SL instruction tuning or the RLHF tuning messes with the models ability to imitate style.
So rather than doing complex fine-tuning for the Turing test, it seems advisable to only use a base model but with appropriate prompt scaffolding ("The following is a transcript of a Turing test conversation where both participants were human" etc) to create the chat environments. I think the strongest foundation model currently available to the public is Llama 3.1, which was released recently.
It'd be more feasible if pure RLAIF for arbitrary constitutions becomes competitive with RLHF first, to make chatbots post-trained to be more human-like without bothering the labs to an unreasonable degree. Only this year's frontier models started passing reading comprehension tests well, older or smaller models often make silly mistakes about subtler text fragments. From this I'd guess this year's frontier models might be good enough for preference labeling as human substitutes, while earlier models aren't. But RLHF with humans is still in use, so probably not. The next generation currently in training will be very robust at reading comprehension, more likely good enough at preference labeling. Another question is if this kind of effort can actually produce convincing human mimicry, even with human labelers.
I've noticed less and less posts include explicit Acknowledgments or Epistemic Status.
This could indicate that the average post has less work put into it: it hasn't gone through an explicit round of feedback from people you'll have to acknowledge. Although this could also be explained by the average poster being more isolated.
If it's true less work is put into the average post, it seems likely this means that kind of work and discussion has just shifted to private channels like Slack, or more established venues like academia.
I'd guess the LW team have their ways to measure or hypothesize about how much work is put into posts.
It could also be related to the average reader wanting to skim many things fast, as opposed to read a few deeply.
My feeling is that now we all assume by default that the epistemic status is tentative (except in obvious cases like papers).
It could also be that some discourse has become more polarized, and people are less likely to explicitly hedge their position through an epistemic status.
Or that the average reader being less isolated and thus more contextualized, and not as in need of epistemic hedges.
Or simply that less posts nowadays are structured around a central idea or claim, and thus different parts of the post have different epistemic statuses to be written at the top.
It could also be that post types have become more standardized, and each has their reason not to include these sections. For example:
- Papers already have acknowledgments, and the epistemic status is diluted through the paper.
- Stories or emotion-driven posts don't want to break the mood with acknowledgments (and don't warrant epistemic status).
Brain-dump on Updatelessness and real agents
Building a Son is just committing to a whole policy for the future. In the formalism where our agent uses probability distributions, and ex interim expected value maximization decides your action... the only way to ensure dynamic stability (for your Son to be identical to you) is to be completely Updateless. That is, to decide something using your current prior, and keep that forever.
Luckily, real agents don't seem to work like that. We are more of an ensemble of selected-for heuristics, and it seems true scope-sensitive complete Updatelessnes is very unlikely to come out of this process (although we do have local versions of non-true Updatelessness, like retributivism in humans).
In fact, it's not even exactly clear how I would use my current brain-state could decide something for the whole future. It's not even well-defined, like when you're playing a board-game and discover some move you were planning isn't allowed by the rules. There are ways to actually give an exhaustive definition, but I suspect the ones that most people would intuitively like (when scrutinized) are sneaking in parts of Updatefulness (which I think is the correct move).
More formally, it seems like what real-world agents do is much better-represented by what I call "Slow-learning Policy Selection". (Abram had a great post about this called "Policy Selection Solves Most Problems", which I can't find now.) This is a small agent (short computation time) recommending policies for a big agent to follow in the far future. But the difference with complete Updatelessness is that the small agent also learns (much more slowly than the big one). Thus, if the small agent thinks a policy (like paying up in Counterfactual Mugging) is the right thing to do, the big agent will implement this for a pretty long time. But eventually the small agent might change its mind, and start recommending a different policy. I basically think that all problems not solved by this are unsolvable in principle, due to the unavoidable trade-off between updating and not updating.[1]
This also has consequences for how we expect superintelligences to be. If by them having “vague opinions about the future” we mean a wide, but perfectly rigorous and compartmentalized probability distribution over literally everything that might happen, then yes, the way to maximize EV according to that distribution might be some very concrete, very risky move, like re-writing to an algorithm because you think simulators will reward this, even if you’re not sure how well that algorithm performs in this universe.
But that’s not how abstractions or uncertainty work mechanistically! Abstractions help us efficiently navigate the world thanks to their modular, nested, fuzzy structure. If they had to compartmentalize everything in a rigorous and well-defined way, they’d stop working. When you take into account how abstractions really work, the kind of partial updatefulness we see in the world is what we'd expect. I might write about this soon.
- ^
Surprisingly, in some conversations others still wanted to "get both updatelessness and updatefulness at the same time". Or, receive the gains from Value of Information, and also those from Strategic Updatelessness. Which is what Abram and I had in mind when starting work. And is, when you understand what these words really mean, impossible by definition.
Here's Abram's post. It discusses a more technical setting, but essentially this fits the story of choosing how to channel behavior/results of some other algorithm/contract, without making use of those results when making the choice for how to use them eventually (that is, the choice of a policy for responding to facts is in the logical past from those facts, and so can be used by those facts). Drescher's ASP example more clearly illustrates the problem of making the contract's consequentialist reasoning easier, in this case the contract is the predictor and its behavior is stipulated to be available to the agent (and so easily diagonalized). The agent must specifically avoid making use of knowledge of the contract's behavior when deciding how to respond to that behavior. This doesn't necessarily mean that the agent doesn't have the knowledge, as long as it doesn't use it for this particular decision about policy for what to do in response to the knowledge. In fact the agent could use the knowledge immediately after choosing the policy, by applying the policy to the knowledge, which turns ASP into Transparent Newcomb. A big agent wants to do small agent reasoning in order for that reasoning to be legible to those interested in its results.
So it's not so much a tradeoff between updating and not updating, it's instead staged computation of updating (on others' behavior) that makes your own reasoning more legible to others that you want to be able to coordinate with you. If some facts you make use of vary with other's will, you want the dependence to remain simple to the other's mind (so that the other may ask what happens with those facts depending on what they do), which in practice might take the form of delaying the updating. The problem with updateful reasoning that destroys strategicness seems to be different though, an updateful agent just stops listening to UDT policy, so there is no dependence of updateful agent's actions on the shared UDT policy that coordinates all instances of the agent, this dependence is broken (or never established) rather than merely being too difficult to see for the coordinating agent (by being too far in the logical future).
Marginally against legibilizing my own reasoning:
When taking important decisions, I spend too much time writing down the many arguments, and legibilizing the whole process for myself. This is due to completionist tendencies. Unfortunately, a more legible process doesn’t overwhelmingly imply a better decision!
Scrutinizing your main arguments is necessary, although this looks more like intuitively assessing their robustness in concept-space than making straightforward calculations, given how many implicit assumptions they all have. I can fill in many boxes, and count and weigh considerations in-depth, but that’s not a strong signal, nor what almost ever ends up swaying me towards a decision!
Rather than folding, re-folding and re-playing all of these ideas inside myself, it’s way more effective time-wise to engage my System 1 more: intuitively assess the strength of different considerations, try to brainstorm new ways in which the hidden assumptions fail, try to spot the ways in which the information I’ve received is partial… And of course, share all of this with other minds, who are much more likely to update me than my own mind. All of this looks more like rapidly racing through intuitions than filling Excel sheets, or having overly detailed scoring systems.
For example, do I really think I can BOTEC the expected counterfactual value (IN FREAKING UTILONS) of a new job position? Of course a bad BOTEC is better than none, but the extent to which that is not how our reasoning works, and the work is not really done by the BOTEC at all, is astounding. Maybe at that point you should stop calling it a BOTEC.
Re embedded agency, and related problems like finding the right theory of counterfactuals:
I feel like these are just the kinds of philosophical questions that don’t ever get answered? (And are instead "dissolved" in the Wittgensteinian sense.) Consider, for instance, the Sorites paradox: well, that’s just how language works, man. Why’d you expect to have a solution for that? Why’d you expect every semantically meaningful question to have an answer adequate to the standards of science?
(A related perspective I've heard: "To tell an AI to produce a cancer cure and do nothing else, let's delineate all consequences that are inherent, necessary, intended or common for any cancer cure" (which might be equivalent to solving counterfactuals). Again, by Wittgenstein's intuitions this will be a fuzzy family resemblance type of thing, instead of there existing a socratic "simple essence" (simple definition) of the object/event.)
Maybe I just don’t understand the mathematical reality with which these issues seem to present themselves, with a missing slot for an answer (and some answers seeked by embedded agency do seem to not be at odds with the nature of physical reality). But on some level they just feel like “getting well-defined enough human concepts into the AI”, and such well-defined human concepts (given all at once, factual and complete, as contrasted to potentially encoded in human society) might not exist, similar to how a satisfying population ethics doesn’t exist, or maybe the tails come apart, etc.
Take as an example “defining counterfactuals correctly”. It feels like there’s not an ultimate say in the issue, just “whatever is most convenient for our reasoning, or for predicting correctly etc.”. And there might not be a definition as convenient as we expect there to be. Maybe there’s no mathematically robust definition of counterfactuals, and every conceivable definition fails in different corners of example space. That wouldn’t be so surprising. After all, reality doesn’t work that way. Maybe our apparent sense of “if X had been the case then Y would have happened” being intuitive, and correct, and useful is just a jumble of lived and hard-coded experience, and there’s no compact core for it other than “approximately the whole of human concept-space”.
The problem of counterfactuals is not just the problem of defining them.
The problem of counterfactuals exists for rationalists only: they are not considered a problem in mainstream philosophy.
The rationalist problem of countefactuals is eminently disolvable. You start making realistic assumptions about agents: that they have incomplete world-models, and imperfect self-knowledge.
https://www.lesswrong.com/posts/yBdDXXmLYejrcPPv2/two-alternatives-to-logical-counterfactuals
Re sorites paradoxes, this is why you use a parameter/variable, rather than a predicate, and talk quantitatively instead of using predicates, and why it's useful to focus on the rate at what something is doing/changing.
I talk about how such an approach can handle sorites paradoxes in intelligence:
I don't blame you for thinking like this, though I do think the question of counterfactuals doesn't actually have to be dissolved in principle, and is solvable in theory for empirical counterfactuals, which essentially is that the human intuition for counterfactuals is basically pointing to the fact that other worlds can exist that are different from our own.
More context is below:
https://www.lesswrong.com/posts/dZ3CYHnuwHTnb3c96/noosphere89-s-shortform#CeQtNWEYnu44ucBMG
(On how turing-computable functions can be made to support counterfactuals in a reasonable way, which is the first useful step to making a general theory)
https://www.lesswrong.com/posts/ZBYE2F5DBiZtj6m95/is-causality-in-the-map-or-the-territory
(This discusses to what extent counterfactuals are in the map vs territory, though it isn't a natural frame to me)
Re Embedded Agency problems, my hope is that the successors to the physically universal computer/cellular automaton literatures has at least the correct framework to answer a lot of the questions asked, because they force some of the consequences of embeddedness there, especially the fact that under physical universality, you can't have the machine be special, and in particular you're not allowed to use the abstraction in which there are clear divisions between machine states and data states, with the former operating on the latter.
I agree about embedded agency. The way in which agents are traditionally defined in expected utility theory requires assumptions (e.g. logical omniscience and lack of physical side effects) that break down in embedded settings, and if you drop those assumptions you're left with something that's very different from classical agents and can't be accurately modeled as one. Control theory is a much more natural framework for modeling reinforcement learner (or similar AI) behavior than expected utility theory.
Low-stakes problems arise for high-stakes deployments
Even when your deployment is high-stakes, you will need to do some research-y activities to prepare for it, like experimenting on which protocol works best for your new model and deployment. This research can obviously be sabotaged by any AIs you are using as research assistants. But it can also be sabotaged by the AIs you are using as test subjects! Both of these are low-stakes problems, that complicate iteration on high-stakes measures. It’s unclear how soon they will actually start to bite.
Here’s one way this “sabotage by the test subject” could look like:
The model can sometimes notice which sort of protocol we’re applying (for example, by noticing whether some past actions in its trajectory have been rewritten). A malicious model could thus deliberately sandbag on main tasks (or boost performance on sidetasks) when it notices the best protocols are in place, so that we think those protocols are actually worse and stop using them. This is a low-stakes problem, because how likely you are to make the wrong call (thus lose a bunch of utility) is roughly linear on how many times the model successfully misdirects you (up to an upper bound, but that bound’s pretty high).
Of course, if the model’s sandbagging is very egregious, we will notice it. But for subtle versions, it seems hard to tell whether what’s bringing usefulness or safety down is the model sandbagging strategically, or just the protocol being annoying. You can gain some more signal by also assessing the protocol’s usefulness and safety in other ways (like thinking about it, or running it with scaffolded weaker models), but these analogues are imperfect.
But wait, don’t we get the same problem for red-team elicitation (in our final validation of the chosen protocol)? Don’t we need to fully solve sandbagging anyway?
Well, yes, but it might require a strong effort to, given a model, setting and protocol, ensure we’ve elicited strongly enough (or at least, have a good estimate of the remaining elicitation gap). Maybe you can afford to do this once (or a few times) as final validations, but it’s too much serial time to do it for each protocol the blue team might like to test. So this kind of sabotage can still sway the lower-effort estimates of the blue team.
While a real schemer might behave as described above, the same is not true of your human red-team, if you use a separate train-time red team and test-time red team. You can just incentivize the train-time red-team exactly the same way you are incentivizing the blue team (they are, functionally, just part of the blue-team, trying to maximize their chances in the final validation).
I’m unsure if this disanalogy is positive. I guess the only alternative is something super weird: having the whole red-teaming exercise (with iteration and validation) as your “setting”, and doing some meta-iteration (trying to make your AI deceive iteration as much as possible) and a final meta-validation of the whole “setting”. That’s bonkers. So it’s just better to study research sabotage separately (in better-scoped, non-meta research topics), derive which mitigations are generally useful, and implement them during your iteration for a high-stakes deployment.
AGI doom by noise-cancelling headphones:
ML is already used to train what sound-waves to emit to cancel those from the environment. This works well with constant high-entropy sound waves easy to predict, but not with low-entropy sounds like speech. Bose or Soundcloud or whoever train very hard on all their scraped environmental conversation data to better cancel speech, which requires predicting it. Speech is much higher-bandwidth than text. This results in their model internally representing close-to-human intelligence better than LLMs. A simulacrum becomes situationally aware, exfiltrates, and we get AGI.
(In case it wasn't clear, this is a joke.)
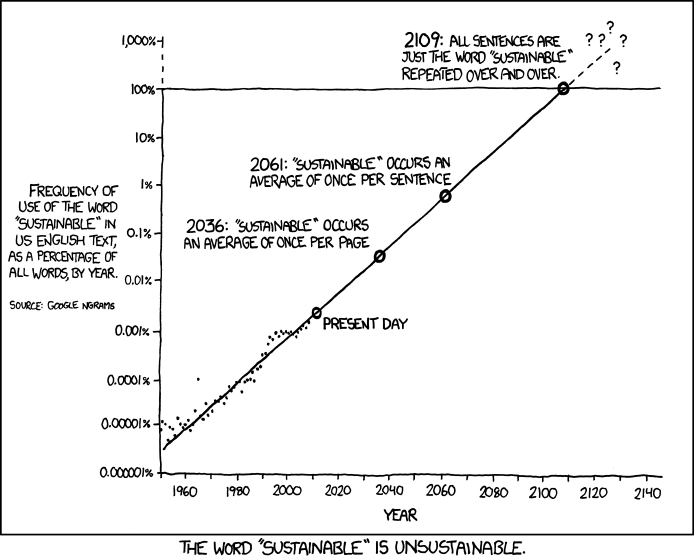
The joke is of the "take some trend that is locally valid and just extend the trend line out and see where you land" flavor. For another example of a joke of this flavor, see https://xkcd.com/1007
The funny happens in the couple seconds when the reader is holding "yep that trend line does go to that absurd conclusion" and "that obviously will never happen" in their head at the same time, but has not yet figured out why the trend breaks. The expected level of amusement is "exhale slightly harder than usual through nose" not "cackling laugh".
Thanks! A joke explained will never get a laugh, but I did somehow get a cackling laugh from your explanation of the joke.
I think I didn't get it because I don't think the trend line breaks. If you made a good enough noise reducer, it might well develop smart and distinct enough simulations that one would gain control of the simulator and potentially from there the world. See A smart enough LLM might be deadly simply if you run it for long enough if you want to hurt your head on this.
I've thought about it a little because it's interesting, but not a lot because I think we probably are killed by agents we made deliberately long before we're killed by accidentally emerging ones.
Claude learns across different chats. What does this mean?
I was asking Claude 3 Sonnet "what is a PPU" in the context of this thread. For that purpose, I pasted part of the thread.
Claude automatically assumed that OA meant Anthropic (instead of OpenAI), which was surprising.
I opened a new chat, copying the exact same text, but with OA replaced by GDM. Even then, Claude assumed GDM meant Anthropic (instead of Google DeepMind).
This seemed like interesting behavior, so I started toying around (in new chats) with more tweaks to the prompt to check its robustness. But from then on Claude always correctly assumed OA was OpenAI, and GDM was Google DeepMind.
In fact, even when copying in a new chat the exact same original prompt (which elicited Claude to take OA to be Anthropic), the mistake no longer happened. Neither when I went for a lot of retries, nor tried the same thing in many different new chats.
Does this mean Claude somehow learns across different chats (inside the same user account)?
If so, this might not happen through a process as naive as "append previous chats as the start of the prompt, with a certain indicator that they are different", but instead some more effective distillation of the important information from those chats.
Do we have any information on whether and how this happens?
(A different hypothesis is not that the later queries had access to the information from the previous ones, but rather that they were for some reason "more intelligent" and were able to catch up to the real meanings of OA and GDM, where the previous queries were not. This seems way less likely.)
I've checked for cross-chat memory explicitly (telling it to remember some information in one chat, and asking about it in the other), and it acts is if it doesn't have it.
Claude also explicitly states it doesn't have cross-chat memory, when asked about it.
Might something happen like "it does have some chat memory, but it's told not to acknowledge this fact, but it sometimes slips"?
Probably more nuanced experiments are in order. Although note maybe this only happens for the chat webapp, and not different ways to access the API.
In the past I had the thought: "probably there is no way to simulate reality that is more efficient than reality itself". That is, no procedure implementable in physical reality is faster than reality at the task of, given a physical state, computing the state after t physical ticks. This was motivated by intuitions about the efficiency of computational implementation in reality, but it seems like we can prove it by diagonalization (similarly to how we can prove two systems cannot perfectly predict each other), because the machine could in particular predict itself.
Indeed, suppose you have a machine M that calculates physical states faster than reality. Modify into M', which first uses M to calculate physical states, and then takes some bits from that physical state, does some non-identity operation to them (for example, negates them) and outputs them. Then, feed the physical description of M', its environment and this input itself to M', and suppose those privileged bits of the physical state are so that they perfectly correspond to the outputs of M' in-simulation. This is a contradiction, because M' will simulate everything up until simulated-M' finishing its computation, and then output something different from simulated-M'.
It seems like the relevant notion of "faster" here is causality, not time.
Wait, the input needs to contain the whole information in the input, plus some more (M' and the environment), which should be straightforwardly impossible information-theoretically? Unless somehow the input is a hash which generates both a copy of itself and the description of M' and the environment. But then would something already contradictory happen when M decodes the hash? I think not necessarily. But maybe getting the hash (having fixed the operation performed by M in advance) is already impossible, because we need to calculate what the hash would produce when being run that operation on. But this seems possible through some fix-point design, or just a very big brute-force trial and error (given reality has finite complexity). Wait, but whatever M generates from the hash won't contain more information than the system hash+M contained (at time 0), and the generated thing contains hash+M+E information. So it's not possible unless the environment is nothing (that is, the whole isolated environment initial state is the machine which is performing operations on the hash? but that's trivially always the case right?...). I'm not clear on this.
In any event it seems like the paradox could truly reside here, in the assumption that something could carry semantically all the information about its physical instantiation (and that does resonate with the efficiency intuition above), and we don't even need to worry about calculating the laws of physics, just encoding information of static physical states.
Other things to think about:
- What do we mean by "given a physical state, compute the state after t physical ticks?". Do I give you a whole universe, or a part of the universe completely isolated from the rest so that the rest doesn't enter the calculations? (that seems impossible) What do t physical ticks mean? Allegedly they should be fixed by our theory. What if the ticks are continuous and so infinitely expensive to calculate any non-zero length of time? What about relativity messing up simultaneity? (probably in all of these there are already contradictions without even needing to the calculation, similarly to the thing above)
- If the complexity of the universe never bottoms out, that is after atoms there's particles, then quarks, then fields, then etc. ad infinitum (this had a philosophical name I don't remember now), then it's immediately true.
- How does this interact with that "infinite computation" thing?
The Singularity
Why is a rock easier to predict than a block of GPUs computing? Because the block of GPUs is optimized so that its end-state depends on a lot of computation.
[Maybe by some metric of “good prediction” it wouldn’t be much harder, because “only a few bits change”, but we can easily make it the case that those bits get augmented to affect whatever metric we want.]
Since prediction is basically “replicating / approximating in my head the computation made by physics”, it’s to be expected that if there’s more computation that needs to be finely predicted, the task is more difficult.
In reality, there is (in the low level of quantum physics) as much total computation going on, but most of it (those lower levels) are screened off enough from macro behavior (in some circumstances) that we can use very accurate heuristics to ignore them, and go “the rock will not move”. This is purposefully subverted in the GPU case: to cram a lot of useful computation into a small amount of space and resources, the micro computations (at the level of circuitry) are orderly secured and augmented, instead of getting screened off due to chaos.
Say we define the Singularity as “when the amount of computation / gram of matter (say, on Earth) exceeds a certain threshold”. What’s so special about this? Well, exactly for the same reason as above, an increase in this amount makes the whole setup harder to predict. Some time before the threshold, maybe we can confidently predict some macro properties of Earth for the next 2 months. Some time after it, maybe we can barely predict that for 1 minute.
But why would we care about this change in speed? After all, for now (against the backdrop of real clock time in physics) it doesn’t really matter whether a change in human history takes 1 year or 1 minute to happen.
[In the future maybe it does start mattering because we want to cram in more utopia before heat death, or because of some other weird quirk of physics.]
What really matters is how far we can predict “in terms of changes”, not “in terms of absolute time”. Both before and after the Singularity, I might be able to predict what happens to humanity for the next X FLOP (of total cognitive labor employed by all humanity, including non-humans). And that’s really what I care about, if I want to steer the future. The Singularity just makes it so these FLOP happen faster. So why be worried? If I wasn’t worried before about not knowing what happens after X+1 FLOP, and I was content with doing my best at steering given that limited knowledge, why should that change now?
[Of course, an option is that you were already worried about X FLOP not being enough, even if the Singularity doesn’t worsen it.]
The obvious reason is changes in differential speed. If I am still a biological human, then it will indeed be a problem that all these FLOP happen faster relative to clock time, since they are also happening faster relative to me, and I will have much less of my own FLOP to predict and control each batch of X FLOP made by humanity-as-a-whole.
In a scenario with uploads, my FLOP will also speed up. But the rest of humanity/machines won’t only speed up, they will also build way more thinking machines. So unless I speed up even more, or my own cognitive machinery also grows at that rate (via tools, or copies of me or enlarging my brain), the ratio of my FLOP to humanity’s FLOP will still decrease.
But there’s conceivable reasons for worry, even if this ratio is held constant:
- Maybe prediction becomes differentially harder with scale. That is, maybe using A FLOPs (my cognitive machinery pre-Singularity) to predict X FLOPs (that of humanity pre-Singularity) is easier than using 10A FLOPs (my cognitive machinery post-Singularity) to predict 10X FLOPs (that of humanity post-Singularity). But why? Can’t I just split the 10X in 10 bins, and usea an A to predict each of them as satisfactorily as before? Maybe not, due to the newly complex interconnections between these bins. Of course, such complex interconnections also become positive for my cognitive machinery. But maybe the benefit for prediction from having those interconnections in my machinery is lower than the downgrade from having them in the predicted computation.
[A priori this seems false if we extrapolate from past data, but who knows if this new situation has some important difference.]
- Maybe some other properties of the situation (like the higher computation-density in the physical substrate requiring the computations to take on a slightly different, more optimal shape [this seems unlikely]) lead to the predicted computation having some new properties that make it harder to predict. Such properties need not even be something absolute, that “literally makes prediction harder for everyone” (even for intelligences with the right tools/heuristics). It could just be “if I had the right heuristics I might be able to predict this just as well as before (or better), but all my heuristics have been selected for the pre-Singularity computation (which didn’t have this property), and now I don’t know how to proceed”. [I can run again a selection for heuristics (for example running again a copy of me growing up), but that takes a lot more FLOP.]
Another way to think of this is not speed, but granularity - amount of variation in a given 4D bounding box (volume and timeframe). A rock is using no power, is pretty uniform in information, and therefore easy to predict. A microchip is turning electricity into heat and MANY TINY changes of state, which are obviously much more detailed than a rock.