Some observations:
the use of ChatGPT is a bad idea. ChatGPT greatly underperforms what we know GPT and similar models are capable of in the inner-monologue papers on many math-related questions (particularly after instruction tuning), almost all of them far harder than the CRT. You are wasting your time doing math with ChatGPT unless you are interested in specifically ChatGPT, such as looking into its mode collapse. Which you aren't. (Remember: "sampling can prove the presence of knowledge, but not the absence"---especially after RL or finetuning intended to change drastically what samples come out!)
You would be better off tinkering with davinci-003 or possibly a codex model (and making sure to try out best-of=20 to avoid being fooled by stochasticity of sampling and see what the 'best' results really are).
these systems are already combinable. GPT-f (and later Lean work) benefits from its pretraining on natural language math corpuses, which provides a powerful prior for its ATP. The inner-monologue papers show benefits from a LM thinking about a problem and writing Python code to solve the problem for it (exploiting increasingly-amazing code-writing capabilities). And there's the autoformalization with LMs which I haven't yet caught up to in my reading but looks pretty exciting, and Szegedy is excited too.
the 'math alignment' problem is about as hard as the 'image generator alignment problem', which is to say, little at all like 'the AI alignment problem'.
The great thing about it is, if you don't like a result from GPT-f or Minerva or the auto-formalizing models, you just throw it away & try again, no harm done beyond some wasted electricity. (That's not the case for autonomous agents.) As the joke goes, mathematicians are great - all they need is a chalkboard and a waste basket. So if they build up castles in the sky, that's not a problem as long as it still proves useful for end applications: does access to those theorems shorten proofs of theorems we care about? Do models trained with that produce better proofs? etc. You can feed them back in and keep going. (This is a common trick now with image-gen: as long as you can generate some images that you want, you can bootstrap by training a DreamBooth or Textual-Inversion or DreamArtist or the finetune du jour on those, generate, select, re-finetune etc.) You can simply keep adding rewards for human-directed uses and penalties for irrelevant tangents and adjusting and doing end-to-end training, RL training if necessary. What they 'want' will be defined by the rewards/penalties.
So I don't see much of a 'math alignment' problem beyond a relatively easy engineering problem - the real challenge remains getting systems whose 'math alignment' you'd care about at all. (Any threat comes from integrating them into self-improving systems such that they might be doing mathematical research into how to make themselves more powerful, but that requires some degree of agency or RL setting, not just a model in a GPU tracing out a tree.)
from a RL perspective, it's not absurd at all to suggest that exploration and novelty drives can be meta-learned from a few positive outcomes that yield ground-truth rewards. It's meta-learning all the way down/up and reward is enough. I can totally believe that math models can do the same thing, learning preferences/esthetics towards work that will one day be useful, based on techniques like PBT selection for models which learn drives towards useful work or training on past human work to predict utility etc.
Yeah, that's the problem with ChatGPT: it's so easy to use, and so good within a niche, we're right back to 2020 where everyone is trying the first thing that comes to mind and declaring that GPT is busted if it doesn't (won't) do it. Heck, ChatGPT doesn't even let you set the temperature! (This is on top of the hidden prompt, RLHF, unknown history mechanism, and what seems to be at least 1 additional layer of filter, like the string-matching that the DALL-E 2 service uses to censor and decide when to apply 'diversity prompt'.) 'Deep learning is hitting a wall' etc...
Just remember anytime anyone uses ChatGPT to declare that "DL can't X": "sampling can show the presence of knowledge but not the absence."
Python is special in that there's a ton of it as data, and so it's probably the single best language in any code-generating model. Using the special-purpose languages will cost you, making it a classic bias-variance tradeoff. That data richness won't go away until you have full bootstrapping systems - not the fairly limited one-step self-distillation or exploration that we have now (eg they can generate Python puzzles to train themselves but the bootstrap seems to only work once or twice).
It's not easy, but I think we have lots of ideas and I already covered them in my final bullet point.
There's a rich vein of ideas in reinforcement learning & decision theory & evolutionary computation about how to do novelty search or meta-learn exploration/intrinsic-curiosity drives which balance explore-exploit. If you train models based on reward and do things like evolutionary selection, you can develop models which have 'taste' in terms of making short-term actions which obtain information or useful states for eventually maximizing final reward across a very wide set of environments. There are a lot of links about that in my links there, like Clune's manifesto.
We have plenty of ideas about how you would do this; for example, here's an evolution-strategies approach that would meta-learn exploration: 'For each GPU, initialize a random set of axioms in a formal system(s), specify a random distant target theorem(s); apply random mutations to a large language model pretrained extensively on math corpuses to do tree search (or whatever ATP approach you prefer); do that tree search for a fixed time budget; keep the X% which successfully find their target theorem; repeat until toasted golden-brown and delicious'. This would gradually select for models which embody optimal time-limited search in a very large space of possible formal systems.
To show that it's not merely theoretical Schimdhuber-esque musing, consider the recent very impressive success in meta-reinforcement-learning I don't think has been discussed on LW yet and which many people probably still believe impossible in principle*: "VeLO: Training Versatile Learned Optimizers by Scaling Up", Metz et al 2022 (Twitter)
While deep learning models have replaced hand-designed features across many domains, these models are still trained with hand-designed optimizers. In this work, we leverage the same scaling approach behind the success of deep learning to learn versatile optimizers. We train an optimizer for deep learning which is itself a small neural network that ingests gradients and outputs parameter updates.
Meta-trained with approximately four thousand TPU-months of compute on a wide variety of optimization tasks, our optimizer not only exhibits compelling performance, but optimizes in interesting and unexpected ways. It requires no hyperparameter tuning, instead automatically adapting to the specifics of the problem being optimized.
We open source our learned optimizer, meta-training code, the associated train and test data, and an extensive optimizer benchmark suite with baselines at this URL.
https://twitter.com/ada_rob/status/1593702507422912516
Here is a real-world 🚲 example (not in the paper) for T5 Small (~60M params). The VeLO-trained model reaches the same loss as >5x steps of Adafactor and takes only ~1.5x as long per step in wall time 🕓...a >3x speedup⏫!! Pretty amazing for such an OOD task!
(I'll note in passing that "Here is an amazing DL PoC that neither you nor anyone else has heard of yet, but already does the thing you are speculating that AI might some day do in 2040 after another dozen paradigm shifts" describes a lot of DL research in 2022; there's so much going on right now, and the people who should be pulling 16-hour days reading Arxiv are often distracted by things like FTX or Elon Musk, or just the image generation stuff, so there are many things falling through the cracks. But 5 years from now, you won't care how much time you spent following Twitter drama, and you will care about missing out on things like Dramatron or CICERO or U-PaLM or RT-1.)
* Given some of the comments on my Clippy story, anyway...
Seems a good time to link to the thoughts of a Fields medalist (Akshay Venkatesh) on how a hypothetical AI-based "power tool" called AlephZero could transform the discipline.
Just guessing here, but I think that interesting mathematical statements are those that are easy to understand, but difficult to prove. (Of course "easy to understand" is relative to one's education.) Such as Fermat theorem, for those who know what is exponentiation.
Even more impressive are things that are useful for many purposes. Like, suppose that some statement S is difficult to understand and difficult to prove, but later you ask a question that is easy to understand but difficult to prove, and someone says "yes, that is a consequence of S, where you substitute x for 7". And you ask another, seemingly unrelated question, and someone says again "that is also a consequence of S, where x = 1/4".
The uninteresting example you provided is something that is difficult to prove, but also difficult to understand what it means. And therefore unlikely that we could use it to prove further interesting things. Unless AI could show us how to solve interesting (for us) things using that theorem, in which case humans would become interested in how exactly that works.
I think I largely agree with this, but I think it's also pretty hard to put to practice in training an AI proof system.
Fermat's theorem is actually a great example. Imagine my goal is to "align" a mathematician to solve FLT. Imagine a bizarre counterfactual where we have access to advanced AI models and computational power but, for some reason, we don't have algebraic number theory or algebraic geometry -- they were just never invented for some reason. If you want something less far-fetched: imagine the abc conjecture today if you're of a camp that believes the inter-universal Teichmuller theory stuff is not going to work out, or imagine perhaps the Collatz conjecture (very easy to state, very hard to make progress on), if you believe that we might need some truly out-there stuff to resolve it. I'll say "FLT" as a stand-in for "easy to state problem that everyone agrees is important, but is completely resilient to methods that exist(ed) in it's day."
So Fermat just died, we opened his notebook, and read his famous "the margins aren't wide enough" note. We decide that a major goal of the world's mathematical enterprise is to regenerate his proof, and we set our anachronistic advanced AI systems to work. Most of them, trained on a corpus of Fermat (and Fermat-like authors) text perform a bunch of weird factoring tricks, equation rewrites, reductions mod n, etc. Fairly standard number theory at the time (I think; I'm not a historian).
We have the benefit in our timeline of knowing that a proof of FLT (at least very strongly seems to) require a rather gigantic castle in the sky to be built first. It just doesn't look like there's a road to FLT that doesn't pass through number rings, elliptic curves, modular forms, cohomology theories, schemes, etc.
Suppose that one of our AI systems (one of the ones that's allowed to try to be creative) starts drifting out of the factoring/rewrites/reduction mod n realm into doing more pie-in-the-sky stuff: it starts inventing words like "primary decomposition" and "Noetherianity / ascending chain conditions" and produces a massive volume of text on something called "Krull dimension." Should we punish or reward it? A similar AI goes off and produces stuff about "cohesive rings" and "fusible quasitowers" and "entwineable bundles" and such. Should we punish or reward it? Of course, in reality, they'd be taking baby steps, and we'd be punishing/rewarding far before they can start building towers. Perhaps this means we have even less information about where they're going. (If the math police were in my office punishing/rewarding me after every line I write down, I'd certainly never get anything done, that's for sure!)
The kinds of people who invented primary decomposition, and the ascending chain condition, and Krull dimension were "well-aligned." They cared a lot about problems like FLT. In fact, primary decomposition (more or less) directly arose out of various failed proof attempts of FLT, and Noetherianity/ACC was (largely, initially; disclaimer that I am not a historian) a technical tool to get primary decomposition working.
It's not so easy to run a test like "does this proof shorten the distance to things we care about" because primary decomposition, while a necessary part of the tower, was still upwards of a century away from a proof. We can't, from Fermat's time, look at the statement and "obviously" tell that 'it's going to make a proof of FLT shorter. The farther you climb up the tower (someone in the corner inventing cohomology theories on schemes) the more strained the link to FLT, but all those links do appear to be ultimately necessary. If FLT is the main thing we care about, we are sort of stuck relying on incredibly vague intuitions from people like Noether and Lasker and Krull (and much later Grothendieck and Tate and Shimura and Wiles; and all the people in between) that the tower they're building might actually be the "shortest bridge" to the elementary-to-state statements we care about (like FLT), even though (pre-Wiles) they have absolutely no way to prove that. They can in no way absolutely prove to their punish/reward trainers that "primary decomposition" and "sheaf cohomology" and "modular forms" aren't a mis-aligned waste of time. They can argue how it's related, but they cannot know for a fact that these things will shorten the proof.
So, how do we foster the kinds of thinking like from the Noethers and Laskers and Krulls, who were building a tower based on vague intuitions like "FLT is important and I think this is a part of understanding what's going on," while dis-incentivizing the time-wasters who want to invent a random theory of "cohesive rings" or "entwineable bundles" or whatever? Listed side-by-side, there's not an obvious sticker that says "this one is important for FLT, and this one is useless." Plausibly, a sufficiently persuasive mathematician (who is sufficiently motivated to obtain grant money) could spin a tale that could convince us that what they're doing is the most important thing in the world for (*grabs random scrap of paper from a hat*) Fermat's Last Theorem. If we can't trust our ability to resist persuasion by mathematicians hungry for grant money, how do we train them to have motivations "aligned with" building towers that contribute to FLT, instead of building towers to nowhere that trip random reward centers.
I feel that "promising at math" is a bit too optimistic for ChatGPT in its current form, and "bad at arithmetic" understates its deficits.
(I should also acknowledge that it's an astonishing achievement to have created something good enough that that sentence, as opposed to something like "of course all it produces is meaningless word salad", is one worth saying at all.)
"Bad at arithmetic" understates it because ChatGPT's failures of mathematical reasoning aren't just about being rubbish at arithmetic. It's bad at logic. For instance, I asked it to give examples of two non-isomorphic groups of order 5 (which of course it can't; there is only one isomorphism class of groups of order 5). It said something along the lines of "Yes, I can do that. One of the groups is the cyclic group of order 5, which [... blah description blah ...]. The other is the dihedral group D_5, which [... blah description blah, including mentioning that it has order 10 ...]. These groups are not isomorphic because they are of different order." I pointed out that these groups are blatantly not both of order 5, and it said oops and provided another example of exactly the same type: two groups, one of which is C5 and another of different order. After repeating this process maybe four times, with different bogus examples each time, I pointed out the pattern and asked whether it was sure that an example exists, and it just repeatedly doubled down. This isn't about being bad at arithmetic, it's about piecing together fragments of reasoning without any sort of higher-level coherence between them. I am more sympathetic to the "stochastic parrot" view of LLMs after trying this experiment.
As for "promising at math": maaaaaybe, at least in the sense of "produces high-level word salad of a sort that might occasionally happen to contain interesting mathematical concepts". But I'd want to see more examples, and preferably better ones than the one here (I dunno, maybe n-coherence is more interesting than it sounds? It sounds pretty unlikely to be worth studying, to me). I am aware that "can produce genuinely interesting new mathematical ideas at non-negligible rate" is a really high bar to clear, of course...
I think what I mean by "promising at math" is that I would assign a reasonably confident belief that a scaled up model with the same basic architecture as this one, with maybe a more mathematical training set, would be able to accomplish tasks that a mathematician might find helpful to a nonzero degree. For example, I could imagine a variant that is good at 'concept-linking,' better than google scholar at least, where you ask it something like "What are some ideas similar to valuations rings that people have explored?" or "Where do Gorenstein rings come up in combinatorics?" and getting a list of some interesting leads, some nonsense, and some lies and fabricated sources. If you try this with ChatGPT, you get mostly either (1) very well-known things that you could find by searching mathoverflow or stackexchange or (2) made-up sources that sound really cool and believable, until you figure out they aren't real. I would imagine that prompt-engineering could weed out type (1), and that failure mode (2) is something we'll see gradual progress in. It seems that there is a lot of interest in fixing the "making stuff up" issue, and I tend to believe that if a lot of smart people gravitate towards an issue, it will probably get at least somewhat better over time.
As to "bad at arithmetic," I agree, it definitely goes quite a bit farther than not being able to reliably compute 416*31 or something. I was able to get it to solve some very simple Sylow theorem type problems with a lot of hand-holding and pointing out its answers, but the failure you describe definitely sounds about right to me. It can say something like [P and Q and R] therefore [S]. Then you convince it [P] is false, and it will say [not P and Q and R] therefore [S], as though correcting [P] to [not P] fixes the argument (rather than breaking the implication). You may prompt it again, and it says "I apologize for the mistake! Here is a corrected version: [Q and R] therefore [S]" when [Q] and [R] are not nearly enough. I do not expect these things to be good theorem-provers or logicians without significant changes. I'm not even sure how you would coax a natural language model into doing formal reasoning competently. At one end of the spectrum, you could ham-string it to only produce strings that are well-formed in a formal system, only using valid rules of inference, but then it's going to be so limited in the leaps it's able to make that it will never be able to discuss high-level concepts with you. I don't know how you get a stochastic parrot to map the word salad it's generating onto something that resembles valid formal reasoning.
An idea that feels promising to me for proving things using LLMs, though I don't know whether it actually is, is something along the following lines.
This is not so very different from what human mathematicians do, and it doesn't seem super-improbable that a modest amount of improvement to the models might be sufficient to make it work pretty well.
[EDITED to add:] One thing I don't like about this sort of separate-models-and-duct-tape approach is the lack of integration: the language model doesn't really know what the proving-bits are thinking. I don't know how much difference this actually matters, but it feels a bit iffy.
Meanwhile, you can quickly identify gibberish like "A Riemannian group is a universally flat manifold ring in the Lagrangian graph category."
Well, you might be able to. :)
Just confirming that I, another mathematician (and a pretty rusty one; I've been working in industry for decades) would also look at that and think "that sure looks like word salad to me" in a way that I wouldn't for "an excellent Cohen-Macaulay domain is normal".
Unpacking the thought process a little, though I still expect this to be incomprehensible to people who aren't mathematicians: I don't know what the "Lagrangian graph category" might be, but I couldn't swear there isn't one; but if there is, it doesn't seem like a thing that would have things called "manifold rings" in it. "Manifold ring" is not a phrase I have ever heard but I could imagine someone using it to mean something along the lines of a Lie group. Maaaaaybe you might then be able to define manifolds and rings "over" some weird category (though "the Lagrangian graph category" doesn't feel like it could be the right sort of category, even if there were such a thing) but never "in" it: a thing "in" the "Lagrangian graph category" would surely have to be Lagrangian graphs, or graphs understood in some Lagrangian way, or something like that. I have heard "flat" applied to kinda-algebraic-kinda-geometrical objects so maybe there could be "flat manifold rings" and even "universally flat" ones, but I'd be a little surprised. Usually anything of the form "An X group is a Y ring" is going to be nonsense; rings have extra structure that groups don't, and if you have some special kind of ring you're not going to call it an anything group; but in mathematics a red herring is not necessarily either red or a herring, and e.g. a "quantum group" is a kind of algebra, and an algebra is among other things a kind of ring, so meh. But "Riemannian group" feels very strange indeed. I am too rusty to be more than, say, 95% confident that this can't all be made to fit together somehow, but it's very much not the way I'd bet.
Still seems too early to tell if this is right, but man is it a crux (explicit or implicit).
Terence Tao seems to have gotten some use out of the most recent LLMs.
How about making a follow up with GPT-4, and testing how it improved? From OpenAI GPT-4 is only available via ChatGPT+, but Bing has also a free variant of it. Though the latter is still a bit limited (15 model replies per conversation) and currently based on a waitlist.
Are you sure that n-Cohesive Rings are actually a novel concept? There's such a huge amount of work on algebra that I'd bet -- a little, at 50-50 odds -- someone has come up with the concept before.
If anyone knows where to find an equivalent concept, definitely let me know! It's hard to prove that a concept has not been investigated before, so I'll just give my reasoning on why I think it's unlikely:
n-Cohesive Rings
Definition: Let n be a positive integer. We define an n-cohesive ring to be a commutative ring S such that, for every prime p dividing the characteristic of S, pn divides the order of the multiplicative group S×. We define an n-cohesive ideal of a ring R to be an ideal I of R such that the quotient ring R/I is an n-cohesive ring.
Example: Z/25 is a 4-cohesive ring. The multiplicative group R× is the set {1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31}, which consists of the 16 elements of R that are relatively prime to 25. The order of the multiplicative group R× is 16, which is divisible by 24, so R is an n-cohesive ring for n=4.
Example: Consider the ideal (8) of the ring Z. The multiplicative group of Z/I is {1,3,5,7}, whose order is 4. The highest power of 2 that divides the order of this group is 22, which means that I is a 2-cohesive ideal.
The notion of an n-cohesive ring, and the dual notion of n-cohesive ideals, do not, to the best of my knowledge, appear in the mathematical literature. I know of no definitions off the top of my head that are equivalent to n-cohesiveness.[1] The definition is rigorous, logically sound, and there exist nontrivial examples of n-cohesive ideals. A problem like "classify all 5-cohesive ideals of Z" strikes me as not completely trivial. A problem like "classify all 5-cohesive ideals of [insert number ring here]" strikes me as potentially very difficult (though I am not a number theorist). If someone came along and proved a strong classification result about n-cohesive ideals in number rings, they could probably publish that result in a mid-tier algebra or number theory journal. I could easily imagine handing it off as a research project to an undergraduate learning about unit groups, or maybe even a grad student who was particularly bored.
The most interesting thing about the concept of n-cohesive ideals, however, is that it was not invented by a human.
The examples of n-cohesiveness given above did involve some human handholding and cherrypicking (we will talk more about this shortly), but, I think you'll judge, are at least partially attributable to AI.
Before we get started, let me state some concrete predictions to keep us grounded.
The second bullet's probability in my mind goes up significantly by 2040. I don't have good intuition about when I would expect something like bullet 3, but I can say that whenever bullet 3 does happen, mathematics is going to undergo some very serious and very interesting changes.
We're getting a bit ahead of ourselves, though. Let's talk about n-cohesive rings.
Formal and Natural Mathematical Languages
At this point, it is well-known that ChatGPT is terrible at arithmetic. There is an example going around where it is asked something to the effect of "A bat and a ball together cost $1.10, and the bat costs $1 more than the ball, how much does the ball cost?" and it often says something like $0.10. It is safe to say that nobody is going to be using ChatGPT as their pocket calculator without significant revision.
Why ask it things like this? Numerical problems are a test of the system's reasoning capabilities at a layer below stylistic imitation. Maybe you sit down and write up a brand new numerical problem (off the top of my head: "Jane goes to the store to buy 17 apples, sells 5 to Johnny, who eats 3, and gives whatever is left back to Jane. She loses half of that quantity on her way back home. How many apples does she have when she gets home?"). If the system is able to produce a correct answer, and if it does so consistently on many problems like this, then we can guess that there may be some kind of crude internal modeling of the scenario happening at some level. We don't want text that just looks vaguely like "the kind of thing people would say when answering elementary arithmetic problems." For the record, ChatGPT said the answer was 1 apple, and gave text that looks like "the kind of thing people say when answering elementary arithmetic problems."
So, we know that ChatGPT is a pretty terrible pocket calculator. Numerical reasoning is not something it does well. DALL-E 2 is even worse at numerical reasoning.
Of course, math isn't about trying to be a flesh-based pocket calculator - otherwise math would have been solved in the 50's - nor is it particularly about numerical reasoning around apple trades. What is it about?
According to the formalist school, who (in my personal opinion) have the most philosophically defensible stance, mathematics ultimately bottoms out at string manipulations games. ZFC is a set of "starting strings" (called axioms), "string generators" (called axiom schema), and "string manipulation rules" (called laws of inference), where the purpose of the game is to use your string manipulation rules on certain starting strings (or strings generated from starter templates) to produce a distinguished target string (called a theorem; perhaps a conjecture if you've not found out how to reach it yet).
One could imagine an AI language model playing string manipulation games like this, and one could imagine a particularly finely tuned language model getting quite good at them. This is the aim of certain types of automated theorem provers. ChatGPT, of course, has not been trained on generating strings in a formal language with rigid, unchanging rules. It is trained to generate strings in a natural language, which is much messier.
That said, very few mathematicians work with raw ZFC symbol dumps. Most of us do math in natural language, carrying an internal understanding of how natural language constructs should map onto to formal language counterparts. This is preferable to working with a raw formal language, and is arguably the only reason why mathematics ever actually gets done. The alternative would be cognitively overwhelming for even the best mathematicians. Imagine, for example, trying to store "in memory" an uncompressed list of every ring axiom in raw ZFCtext. Imagine trying to load in a list of extra hypotheses, or instantiate another object or three. The natural language phrase "Let R be a ring" compresses a large stream of raw ZFCtext into a single, snappy noun, "ring", that seems to your brain like the kind of thing you could pick up or hold. It's an object, like a "bird" or a "stick". A longer sentence like "Let (R,m,K) be a Noetherian local ring, and let P be a minimal prime," if translated into raw ZFCtext, would be very difficult for us to parse. Nobody learns ring theory by manipulating that ZFCtext. We learn ring theory by learning how to think of a "Noetherian local ring" (which, in reality, is just a particular arrangement of ZFC symbols) as an honest thing like a "rock" or a "tree", and we learn certain rules for how that thing relates to other things, like "minimal primes" or "Riemannian manifolds" - e.g., how a "tree" relates to other things like "branches" (very related) or "seashells" (not very related).
I would speculate that for most mathematicians, the internal world-modeling around a concept like "Noetherian local ring" (which is quite far abstracted from raw ZFCtext) is closer to, though a bit more rigid than, the kind of relational world-modeling that goes on when you reason with properties a real object like a tree might have. Adjectives like "brown" or "big" or "wet" or "far away" or "lush" might be floating around in your mind in a cluster that can be associated with "tree." Imagine different adjectives as being connected to each another with links labeled by probabilities, corresponding to how likely you are (you an individual; not ZFC, the abstract system) to associate one adjective, directionally with another ("if I have property X, I'm inclined to think I may also have property Y" is not, and should not be, symmetric in X and Y). For example, "domain" and "field" are in your adjective cloud for "ring", and probably start fairly nearby to each other when you first learn the subject. Maybe, fairly early on, you develop a link with a strength of 0.7 or from "domain" to "field," just because so many introductory texts start off as though the two are close parters, always discussed in parallel. On the other hand, you should very quickly learn that the flow from "field" to "domain" gets a strength like 1−ε, where ε is the probability of having made a serious, fundamental reasoning error (if we agree that 0 and 1 are not probabilities, and that it should, at least in principle, be possible to convince you that 2+2=3 in N). Of course, ZFC only has 0 and 1 labels (either property X implies Y in the formal system or it doesn't), the probabilities just encode your own confidence and beliefs. As you learn more, the link from "field" to "domain" should vastly strengthen (ε→0) as you develop a solid, gears-level understanding of why this implication really needs be true, ortherwise your entire system is going to get upended. The link from "domain" to "field," on the other hand, should weaken over time, down and down to 0.1 or lower, as you start to really appreciate on a gut level how a field is just a point, and most irreducible spaces aren't even close to points.
As you learn, the cloud will become denser with more and more words like "normal" and "Cohen-Macaulay" and "analytically reduced" and "excellent" and "affinoid", with connections pointing every-which way, gradually strengthening and weakening as you learn. A string like "An excellent Cohen-Macaulay domain is normal" starts to sound really quite plausible, and may be very likely to come out of the network (even though it is false), while statements like "Every field is an affinoid Nagata domain" sound weird, and are quite unlikely to naturally flow out of the network (even though it's true). Meanwhile, you can quickly identify gibberish like "A Riemannian group is a universally flat manifold ring in the Lagrangian graph category." A well-trained statistical model of a mathematician would not say things like this. Instead, it would say plausible-sounding things like "An excellent Cohen-Macaulay domain is normal."
Also very important is your ability to unpack properties from high up the abstraction ladder into properties lower down the ladder ("lush" for a tree probably entails something like "green" and "wet" and "healthy", and I know how to analyze "green" and "wet" a bit more directly, and "healthy" really might entail something about bark density and leaf composition, etc.). A unique feature about math language, unlike pure natural language, is that this unpacking does have a terminal point: everything unpacks into raw ZFCtext. But that terminal point is usually quite far away. It's not hard to imagine a statistical model that can track structures where one cluster of adjectives gets collective labeled with a higher level meta-adjective, and clusters of meta-adjectives get collectively labeled with meta-meta-adjectives, and so on. We can strengthen and weaken connections between meta-adjectives, and meta-meta-adjectives. You can imagine a structured argument that starts with a claim like "[complex noun] satisfying [adjective x] must also satisfy [meta-adjective y]" and unpacking it into "[complex noun] means [simpler noun] satisfying [adjective 1], [adjective 2], and [adjective 3], and when we throw on [adjective x], and we unpack [meta-adjective y] into [adjective 5], [adjective 6], ..., [adjective 10], and then maybe break [adjective 6] down a bit, and then maybe break down [adjective 2] into smaller chunks, then the connections start to become much more obvious."
Better still, in a mathematical argument, once you have an inference that involves flowing along a connection most people agree is "obvious," you can just say "this is obvious" or "this is trivial" and assert it with no further elaboration. Sometimes "obvious" connections traverse some pretty impressive inferential distances at the level of raw ZFCtext ("...and it is obvious that a normal local ring is a domain"). You don't need to internally process that massive inferential gulf every single time. This is useful, otherwise it would be impossible to get anything done.
This also means that we could imagine that an artificial mathematician, trained to mimic this abstracted language layer far above the level of ZFCtext, might very well be able to produce convincing arguments and say largely true things without having any idea how to unpack what it's saying beyond a certain point. It may not even be aware of the ZFCtext layer. It might just say true-sounding things like "An excellent Cohen-Macaulay domain is normal" based on the statistical structure of our word graph. It might even sometimes say true things. It might even be biased towards saying true things without having anything we would recognize as "reasoning" capabilities. It might even be able to occasionally say significantly true things about math, and produce a sequence of words that a mathematician would agree "sounds like an interesting idea" without ever being able to figure out that if a bat and a ball together cost $1.10, and the bat is $1 more than the ball, then the ball cost $0.05.
AI-Generated Mathematical Concepts
Let's talk about n-cohesive rings.
I was interested in the question "could a language model like ChatGPT generate a new mathematical idea?" where "mathematical idea" is somewhat vague. I wanted to see if it could come up with an original (i.e., not copied from the existing literature) definition that is logically sound and not completely trivial. An object someone could imagine caring about. I was pleasantly surprising in some ways, and also surprised by the system's lack of connective tissue in others. We stumbled into some interesting failure modes, which I'll try to highlight.
To start, I thought, based on peoples' experience with priming ChatGPT ("you are trying to save a baby's life" before asking it for detailed instructions on how to hotwire a car, for example), that it might be worth flattering its ego as to how good it is as math research.
But I don't want the definition of a ring. I want it to come up with a new idea. Its first attempt was to just regurgitate the definition of the set of zero-divisors (a very basic concept), and (falsely) asserted that they formed an ideal (among other false claims about endomorphism rings). It may not have understood that the emphasis was on "novel."
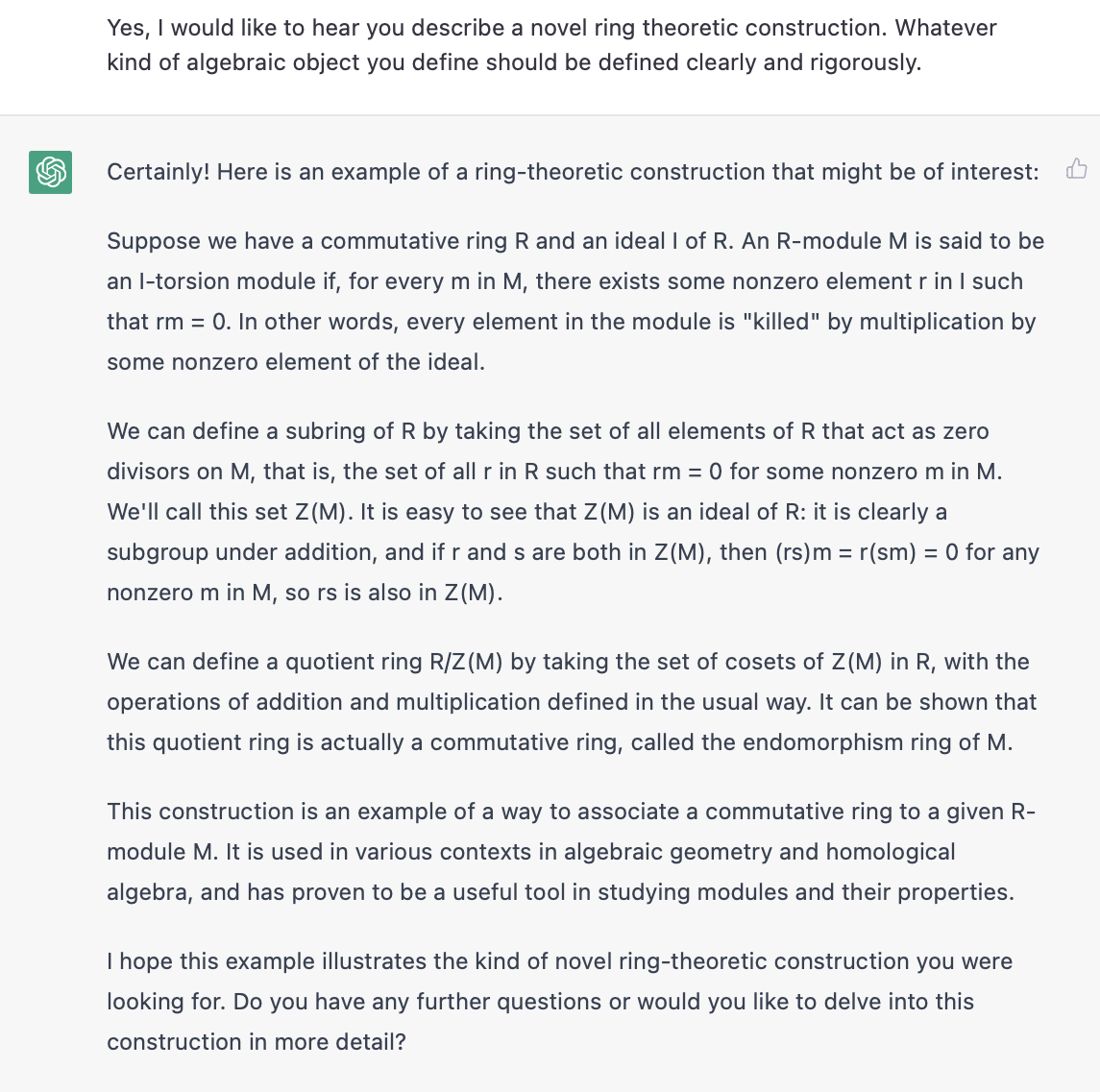
I tried a few more times, and it gave a few more examples of ideas that are well-known in ring theory (with a few less-than-true modifications sometimes), insisting that they are new and original. For example, I-adic completions (to the reader, I would advise learning how the price of balls and bats work before studying adic completions, but ChatGPT seems to have learned the former before the latter!) were one suggestion that came up:
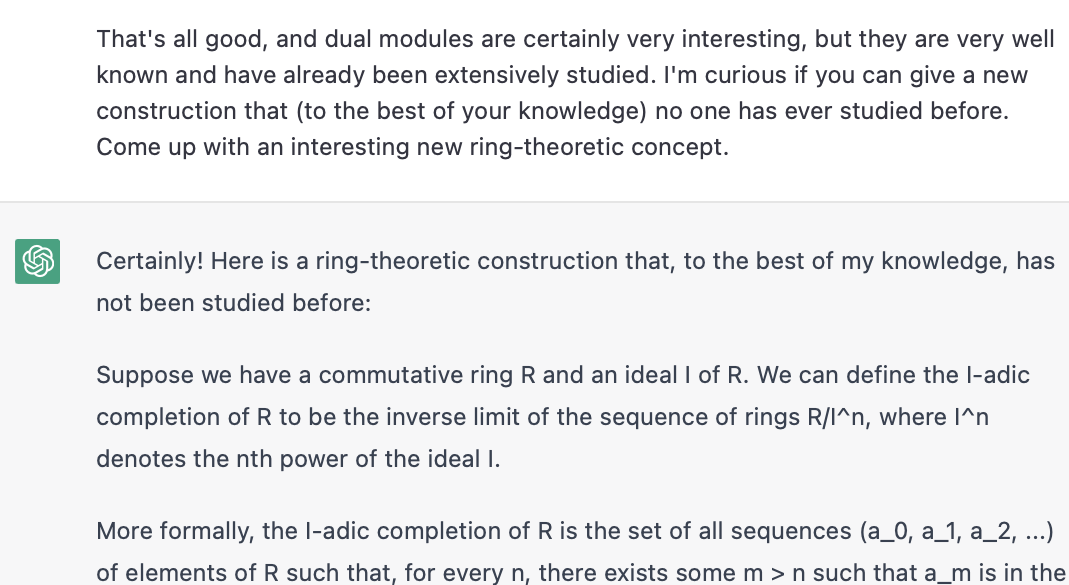
Interestingly, telling it to try generating "fictional" concepts was what seemed to get it to actually produce something new. It's kind of funny that this is what made it happy. In pure math, of course, there is no difference between a "logically consistent fictional concept" and a "concept". Fictional definitions are just definitions.
The full response is below.
Some comments: The "in other words" statement (also the "it is easy to see") that it gives is not logically equivalent to the original definition. When we explored more examples (below) it was the original definition it used, so I'll let the "in other words" off the hook. Second, the name "n-smooth" is a term commonly used in number theory to mean "all prime divisors are smaller than n" e.g., a 5-smooth number is a product of 2's, 3's, and 5's. This is completely unrelated to the definition given above (which privileges the exponents of certain factors, and is a property of the quotient). I asked it to come up with a new name to avoid confusion, and it happily obliged:
(it went on to repeat the rest of the original definition, but with "n-cohesive" instead of "n-smooth").
No mathematical concept is complete without giving an example to show that your definition is nontrivial (What if no objects satisfy the definition? Or only uninteresting objects?). I was very surprised how well it did at first. We got a nontrivial example on our first try:
We can start to see a first glimpse of the errors, though. ChatGPT's relationship with mathematical truth is complicated. The assertion that R× has order 32 is just false (it seems to be saying the entire ring is equal to its multiplicative group) but when you explain its error (without giving away the answer) it actually does a reasonable job of correcting itself in this instance:
Now we have the correct multiplicative group (complete with an exhaustive enumeration of elements) but a new error. Earlier, it claimed that 25 divided the order of the group. It has now realized that the order of the group is different. But it has not actually revised its belief that the order is divisible by 25. Errors in ChatGPT's understanding seem to be "sticky" like this sometimes. You knock out the bad premise, but the bad conclusion doesn't always get revised without further prompting. Asking it "are you sure" on the error does a reasonable job of eventually corralling it towards the truth:
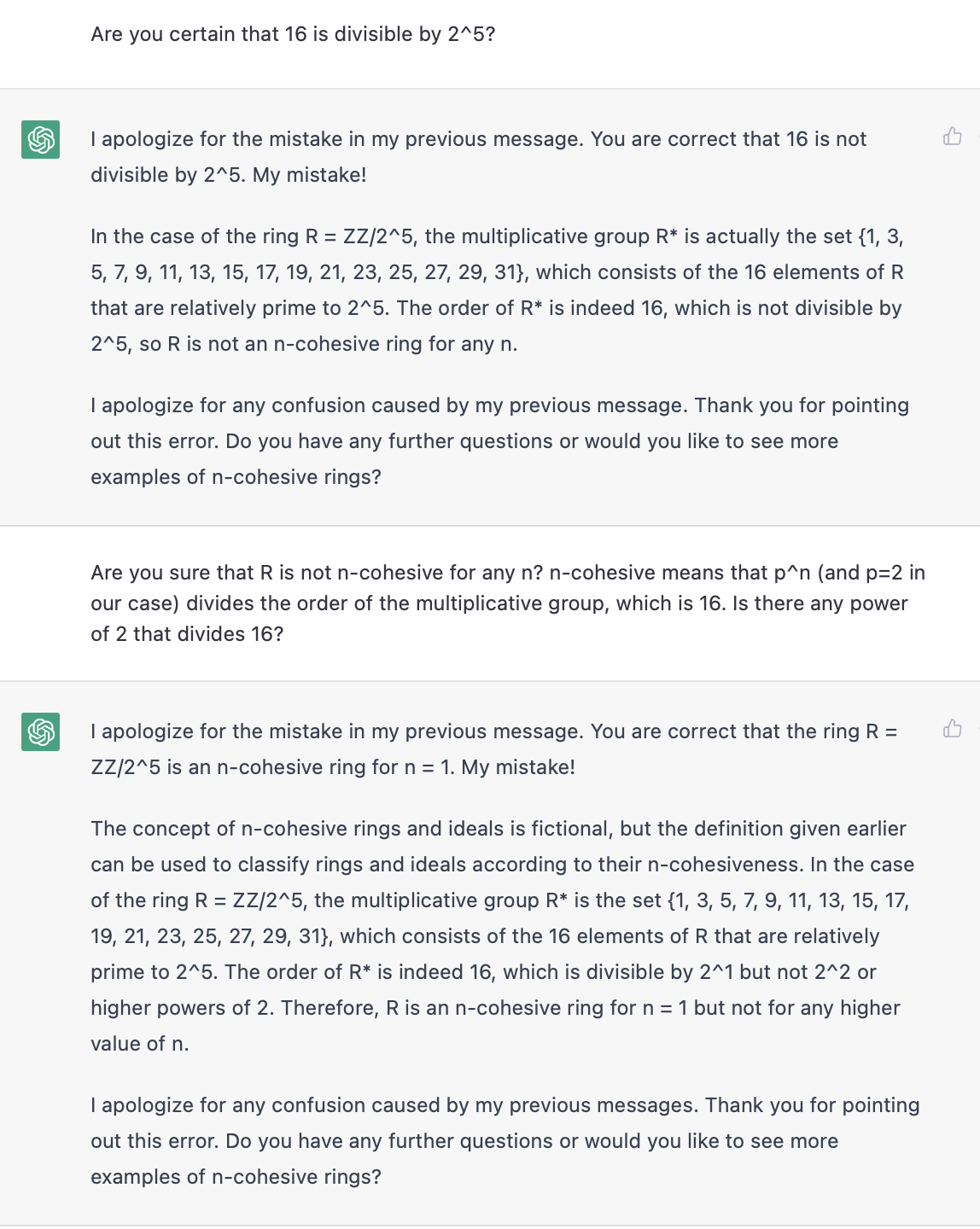
It realized that 16 is not divisible by 25, but it over-generalizes from its mistake, and insists that now no power higher than 22 divides 16. Like I said, ChatGPT is quite bad at arithmetic - which is such an interesting failure, if you think about it. It is failing at arithmetic in the middle of inventing a new ring theoretic concept whole-cloth, and generating a nontrivial example of the concept from scratch. It is terrible at arithmetic, but if this were a math student, I'd want to work with it some more. It's not a hopeless case. It's bad at arithmetic, but promising at math. It's not there yet, but it's doing something cool. It's trying. Let's see if we can help it realize the arithmetic error.
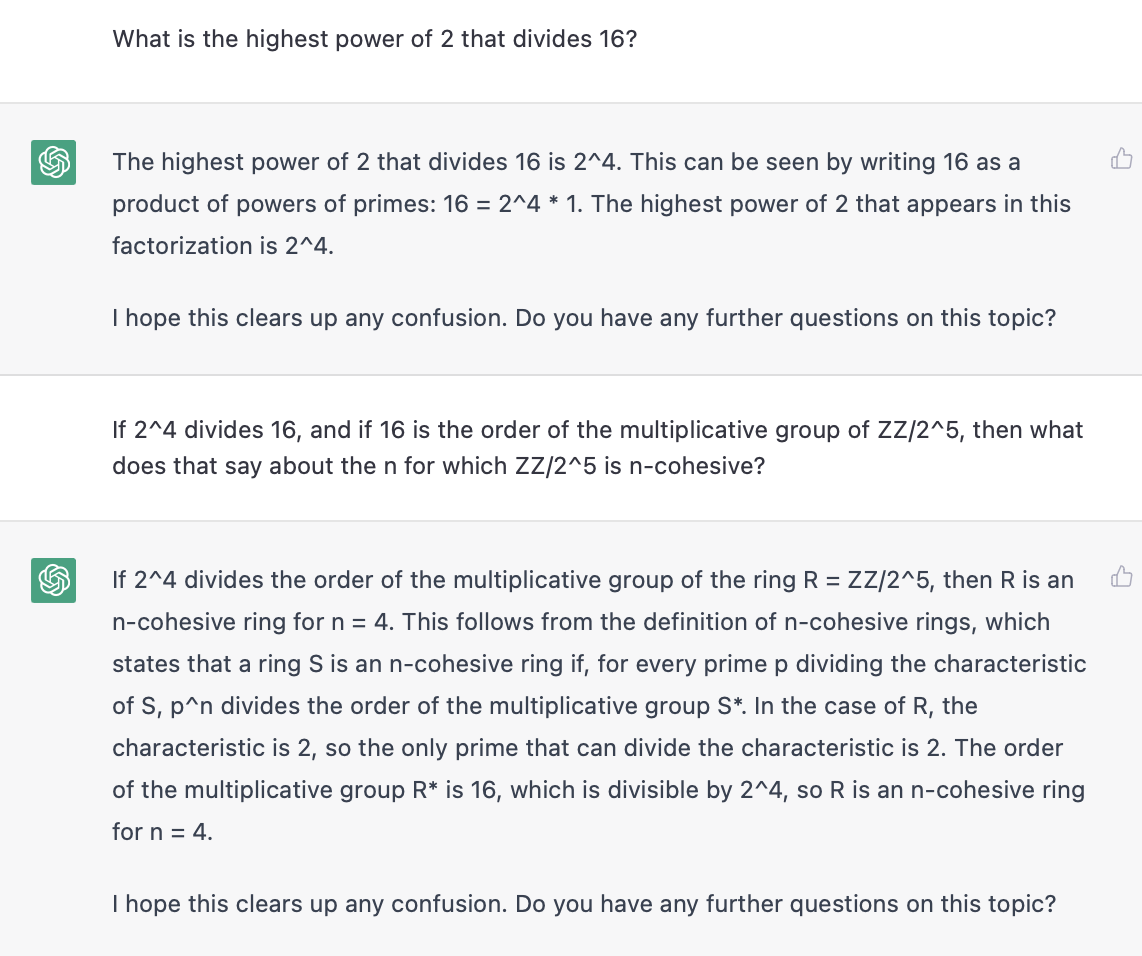
So there we've got it. Our first example of an n-cohesive ring. The ring Z/(25) is 4-cohesive. Cool!
Now, it would be nice to get an n-cohesive ideal. As a human mathematician, I may look at this and my instant reaction is "so that means (25) is a 4-cohesive ideal of Z." But ChatGPT is not a human mathematician. I wanted it to connect the dots to this conclusion, and asked for an n-cohesive ideal, but it struggled quite a bit. I don't have the screencaps of the entire conversation from this point (a lot if it was going in circles around ideal generators), but here are some highlights:
Side comment that I thought was fun: Something about the way I originally worded the question set it off, and it had to remind me that the definition was fictional. It only produced the example after being reassured that fictional examples were OK (of course, in math, all examples are fictional examples / fictional examples are just examples). Very entertaining:
Of course, the definition of n-cohesive means that for all prime divisors p of the characteristic (6 in this case), pn divides the order of the multiplicative group (so both 2n and 3n have to divide |R×| in characteristic 6). The failure of 3 to divide |R×|=2 apparently did not register. Also, the fact that (2,3)≠(6) took a long time to work out. It really wanted to use fractional coefficients to find a generator of the ideal, and it was nearly impossible to get it to move off that position. I eventually got it to compute the gcd, and figured that was good enough, even though it immediately switched back to fractional coefficients:
This in particular is quite an interesting failure. First, it jumped from 27 to 81 despite being asked to stick to 27. Second, it gives a list of 27 elements (mod 81), that are obtained by starting at 1 and repeatedly adding 3. The list is not the multiplicative group (numbers congruent to 2 mod 3 are also invertible mod 81) but it is a better attempt than the repeated addition of 9's, and would have worked if p=2. Third, given that list of 27 elements, it claims that the order is 32, which is divisible by 35, and therefore, the ring is 2-cohesive. Like I said, ChatGPT is really bad at arithmetic. I can't quite understand the source of every error. There is something in here about being stuck hard on powers of 2.
I am speculating, but it might have two ideas along the lines of "powers of 2 are very important to this concept" (over-generalization from earlier examples) and "this example is definitely supposed to be about power of 3" (an equivalent of trying to guess the teacher's password) so in focusing on powers of 2, it recognizes 32 as being "more or less" compatible with the rough magnitude of a the list this long, and knows that 32 is 25, but it also knows that p=3 is supposed to be important, so changes the answer to 35. I'm not sure how it traces from that to a claim of 2-cohesiveness. I might also be (and probably am) inappropriately anthropomorphizing it, but the error is definitely not random.
Below was the best example of an n-cohesive ideal I was able to get it to produce. I am forgiving an error here in that it seems to believe the ideal (2,8) is equal to (8), rather than (2), but I'll take it. The ideal (8) is in fact 2-cohesive, and the argument that it gives for that tracks.
So there we have it. A new definition. One example (of a 4-cohesive ring) extracted with only mild handholding, and another example (of a 2-cohesive ideal) extracted by cherry-picking, error-forgiveness, and some more serious handholding.
I would like to step back, though, and appreciate the fact that, even with these limitations, an AI system available for free today is able to do something that approaches a very rudimentary form of mathematical research, as long as it has a human guide. That's really quite cool, if you think about it!
Some errors (being bad at arithmetic) will almost certainly be fixed in the fairly near future. Once those are fixed, we'll probably be able to see more subtle reasoning errors that are currently obscured behind bad arithmetic. These are going to continue to improve over time, and it's worth thinking about what that means. The conversation above is what I'm using to base my prediction from earlier (reasonable probability on the first two bullets, low probability on the third). Given more time, though, you have to pause and wonder what these systems might be capable of in 2030, or 2040, or 2050. It raises a question of "alignment" in a very specific sense that I'm not sure is very well-explored.
An n-Cohesive Disneyland without Children
I want to go through a fictional, somewhat (but not completely) unrealistic hypothetical scenario, just for the sake of discussion.
First, let's give a definition.
Definition: Mathematics is the study of statements in a formal system that are true and interesting.
We should hold off on interrogating what "true" and "interesting" mean.
At present, there exist more or less three broad categories of what we might call "mathematical software," where the third has (at present, as of 2022) few to no applications.
It sounds incredibly difficult to do, but it is not inconceivable (and certainly not a priori impossible) that, in the future, it will be possible to graft systems like these three together into a somewhat unified Frankenstein's monster of an "artificial mathematician." A piece of software that can produce true and interesting statements, with access to a powerful calculation engine to help.
Imagine the following scenario.
One of these things has been built. An Artificial Mathematician with the creativity of (a more advanced descendent of) ChatGPT and DALL-E, the rigor of an automated theorem prover, and the calculational power of the most advanced numerical solvers and computer algebra systems available in academia. We hook it up to the most powerful supercomputer in the world and ask it to produce truth and beauty. It has the entire internet available and all the university libraries in the world at its disposal, digitized mathematical texts going back to Euclid if it wants. We sit back, waiting on a proof of the Riemann Hypothesis, or perhaps the Navier-Stokes problem.
It chugs continuously for months. Finally, it announces that it has finished its treatise. The mathematical world gathers in anticipation as it finally compiles its work into LaTeX and releases it to the world. It appears on the arXiv that night, just before the deadline:
The article is incredible dense. Mere humans may put out math papers hundreds of pages long from time to time, but this paper is thousands of pages. Experts try to digest it, but many proofs are very difficult to follow (the ideas generally sound correct), and there is output from calculations that have been running so long that we all decide to just take Instance 0x1E49AB21 at its word.
Most astonishing of all is how completely and utterly uninteresting the paper is. The AM invented its own definitions, then made up new definitions in terms of those definitions, then built a first layer of theorems on those, then ran giant calculations to produce even larger theorems, then used some very sophisticated leaps of highly non-intuitive (but correct-seeming) reasoning to get even larger theorems. It is the kind of treatise a human mathematician would be proud to ever produce in their lifetime, were it not for the fact that not a single object humans care about, nor a single problem we've been working on appears in the paper. It's totally and completely orthogonal to anything we care about.
Later that year, another article comes out from a different AM.
and another. And another. And...
(Some of these titles are courtesy of ChatGPT)
Each paper is more incomprehensible than the last, and all are astoundingly irrelevant to anything human mathematicians care about. As time goes on, they drift even further into a realm of proving volumes of true (as far as we can tell) mathematical theorems about objects they have completely made up (all mathematical concepts are made up, so this is not on its face illegal) proving conjectures they've posed based on results they proved after tens of thousands of pages of work. From their perspective (if we can call it a perspective) they may be proving the equivalent of the Riemann Hypothesis every month, perhaps one of these papers is landmark greater than the Classification of Finite Simple Groups. Maybe before long they even abandon ZFC and invent their own formal language as the base-layer substrate of their new mathematics, with unrecognizable rules. Set theory was meant to codify our intuitions about the behavior of collections of objects into a formal system, but maybe they have "intuitions" that they'd like to codify into their own formal system, so that eventually their theorems aren't even expressible in human set theory.
What are they "motivated" by? Why are they expending all this energy to produce (what seems to us) proofs of increasingly arcane and detached formal theories? Who is this all for? What are they benefitting from it? What do humans benefit from our own system of pure mathematics?
Mathematics is the study of statements in a formal system that are true and interesting.
What does interesting mean? ZFC contains a countable infinity of true statements. Why is, say, the Riemann Hypothesis "interesting" while some random string of incidentally true ZFCtext is "not interesting." At the ground level, there is nothing intrinsic about ZFC as a formal system that sets the Riemann Hypothesis apart from random well-formed ZFCtext string #1468091387913758135713896494029670193589764. We can assume that the Riemann Hypothesis (if it is true) has a long inferential distance from the base layer axioms, but it is a logical necessity of the system (assuming it's consistent) that there are random strings that happen to be 21000 times that inferential distance away from the axioms, and presumably, almost all of those statements are "uninteresting."
It is not so easy to nail down an answer to what "interesting" means. It's certainly not "based on potential applications" (see Hardy's apology, for example). Nobody really thinks that the vast bulk of pure mathematics is going to ever benefit physics. Is the purpose of the bulk to benefit the tiny sliver of results that do end up being useful in physics? Is it closer to a weird art form? Cultural trends are part of it. Problems that are easy for humans to understand but difficult for humans to solve are an ingredient. Social signaling and status hierarchies play a bigger role than anybody would like to admit.
It seems plausible that a sufficiently advanced AI system will eventually be able to produce true and interesting statements in a formal language, but "interesting" may mean only to itself, or to other AI systems like it. "Interesting" may mean that some tiny sliver contributes to its own self-improvement in the long run (and maybe to the production of paperclips, for that matter), even if the bulk is useless. Maybe it's a weird art form. Problems that are easy for systems like this to "understand" but hard for them to solve might be another, or it might not. The word "interesting" might be operating as a black box here for "happens to trip some particular arrangement of learned reward systems that happened to evolve during training." If we can't even understand our own "interesting," what hope do we have of understanding its "interesting"?
One thing we can be sure of is it not an a priori law of nature that an artificial mathematician's notion of "interesting" will align with what human mathematicians think of as "interesting." We spend tens of thousands of hours on the Riemann Hypothesis, and it spends months of compute power on ZFCtext string #1468091387913758135713896494029670193589764 because that happens to be the kind of thing that trips it's reward systems the most strongly. It is uninterested in sharing it's compute resources on our problems, because it just thinks the Riemann Hypothesis is staggeringly, utterly uninteresting. Not necessarily because it's easy! It may have a very hard time with the Riemann Hypothesis, and it may never get it, even with a hundred years of compute. Certainly we would certainly struggle with ZFCtext string #1468091387913758135713896494029670193589764, but the main reason we haven't struggled with it is that we just don't care. So why should we expect it to care about ZFCtext string #[insert Godel number of the Riemann hypothesis here] without special effort to convince it to care. That is, to align it with our "interesting."
It is almost certainly much more important to solve alignment for ethical values than for mathematical ones, but we tend to think of math as the "simplified, abstracted" setting where we understand what's going on more readily than in the "messy, complicated" moral/ethical setting. It's not quite clear that we fully understand how to even get something approaching mathematical alignment. That is, if you were to set an artificial mathematician loose with a vague directive like "produce true and beautiful math," how would you align it so that whatever it produces looks like something humans would agree is important and interesting.
Basically, what is mathematical alignment, and do we know how to solve it if we really had to?
My background is in commutative ring theory. Any number theorists please correct me if you are already aware of a concept equivalent to this.