Innate Mathematical Ability

JonahS

75 Innate Mathematical Ability

18th Feb 2015

11 min read

75

In my present sequence of posts, I'm writing about the nature of mathematical ability. My main reason for doing so is to provide information that can help improve mathematical ability.

Along the way, I'm going to discuss how people can't improve their mathematical ability. This may seem antithetical to my goal. Focus on innate ability can lead to a sort of self-fulfilling prophesy, where people think that their abilities are fixed and can't be improved, which results in them not improving their abilities because they think that doing so is pointless.

Carol Dweck has become well known for her growth mindset / fixed mindset framework. She writes:

"In a fixed mindset students believe their basic abilities, their intelligence, their talents, are just fixed traits. They have a certain amount and that's that, and then their goal becomes to look smart all the time and never look dumb. In a growth mindset, students understand that their talents and abilities can be developed through effort, good teaching and persistence. They don't necessarily think everyone's the same or anyone can be Einstein, but they believe everyone can get smarter if they work at it." [...] This is important because individuals with a "growth" theory are more likely to continue working hard despite setbacks...

As I'll describe in my next post, I'm broadly sympathetic with Dweck's perspective. But it's not an either-or situation. Some abilities are innate and can't be developed, and other abilities can be.

One could argue that this idea is too nuanced for most people to appreciate, so that it's better to just not talk about innate ability. This seems to me paternalistic and patronizing. People need to know which abilities are fixed and which can be developed, so that they can focus on developing abilities that can in fact be developed rather than wasting time and effort on developing those that can't be.

Working to improve abilities that are fixed is unproductive

When I was in elementary school, I would often fall short of answering all questions correctly on timed arithmetic tests. Multiple teachers told me that I needed to work on making fewer "careless mistakes." I was puzzled by the situation – I certainly didn't feel as though I was being careless. In hindsight, I see that my teachers were mostly misguided on this point. I imagine that their thinking was:

"He knows how to do the problems, but he still misses some. This is unusual: students who know how to do the problems usually don't miss any. When there's a task that I know how to do and don't do it correctly, it's usually because I'm being careless. So he's probably being careless."

If so, their error was in assuming that I was like them. I wasn't missing questions that I knew how to do because I was being careless. I was missing the questions because my processing speed and short-term memory are unusually low relative to my other abilities. With twice as much time, I would have been able to get all of the problems correctly, but it wasn't physically possible for me to do all of the problems correctly within the time limit based on what I knew at the time. (The situation may have been different if I had had exposure to mental math techniques, which can substitute for innate speed and accuracy.)

Even at that age, based on my introspection, I suspected that my teachers were wrong in their assessment of the situation, and so largely ignored their suggestion, while at the same time feeling faintly guilty, wondering whether they were right and I was just rationalizing. I made the right judgment call in that instance – making a systematic effort to stop making "careless errors" under time constraints wouldn't have been productive. To avoid such waste we need to delve into a discussion of innate ability.

Intelligence and innate mathematical ability

I think that mathematical ability is best conceptualized as the ability to recognize and exploit hidden structure in data. This definition is nonstandard, and it will take several posts to explain my choice.

Abstract pattern recognition ability

A large part of "innate mathematical ability" is "abstract pattern recognition ability," which can be operationalized as "the ability to correct answer Raven's Matrices type items." Tests of Raven's Matrices type are perhaps the purest tests of IQ: the correlation between performance on them and the g-factor is ~0.8, as high as any IQ subtest, and answering the items doesn't require any subject matter knowledge. One example of an item is:

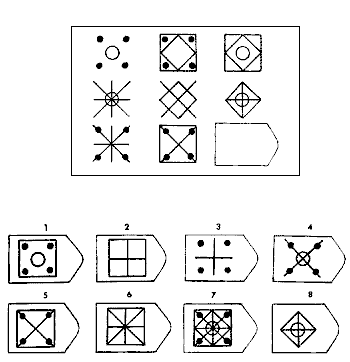
The test taker is asked to pick the choice that completes the pattern. People who are able to pick the correct choice at all can usually do so within 2 minutes – the questions have the character "either you see it or you don't." Most people can't see the pattern in the above matrix. A small number of people can see much more subtle patterns.

There's fairly strong evidence that something like 30% of what differentiates the best mathematicians in the world from other mathematicians is the innate ability to see the sorts of patterns that are present in very difficult Raven's matrices type items. (I'll make what I mean by "something like 30%" more precise in a future post.)

Fields Medalist Terry Tao was part of the Study of Mathematically Precocious Youth (SMPY). Professor Julian Stanley wrote:

On May 1985 I administered to [10 year old] Terry the Raven Progressive Matrices Advanced, an untimed test. He completed its 36 8-option items in about 45 minutes. Whereas the average British university student scores 21, Terry scored 32. He did not miss any of the last, most difficult, 4 items. Also, when told which 4 items he had not answered correctly, he was quickly able to find the correct response to each. Few of SMPY's ablest protégés, members of its "700-800 on SAT-M Before Age 13" group, could do as well.

People like Terry are perhaps 1 in a million, but I've had the chance to tutor several children who are in his general direction.

Descriptions of milestones like "scored 760 on the math SAT at age 8" (as Terry did) usually greatly understate the ability of these children when the milestone is interpreted as "comparable to a high school student in the top 1%," in that there's a connotation that the child's performance comes from the child having learned the usual things very quickly. The situation is usually closer to "the child hasn't learned the usual things, but is able to get high scores by solving questions ththat high school students wouldn't able to able to solve without having studied algebra and geometry."

A impact of interacting with such a child can be overwhelming. I've repeatedly had the experience of teaching such a child a mathematical topic typically covered only in graduate math courses, and one that I know well beyond the level of textbook expositions, and the child responding by making observations that I myself had missed. The experience is surreal, to the point that I wouldn't have been surprised to learn that it had all been a dream 30 minutes later.

I'll give an example to give a taste of a visceral sense for it. In one of my high school classes, my teacher assigned the problem of evaluating 'x' in the equation below:

Tangentially, I don't know why we were assigned this problem, which is of considerable mathematical interest, but also outside of the usual high school curriculum. In any case, I remember puzzling over it. Based on my experiences with children similar to Terry, it seems likely that his 8-year old self would see how to answer it immediately, without having ever seen anything like the problem before. Roughly speaking, an 8-year old child like Terry can recognize abstract patterns that very few (if any) of a group of 30 high school students with the math SAT score would be able to recognize.

In A Parable of Talents, Scott Alexander wrote:

IQ is so important for intellectual pursuits that eminent scientists in some fields have average IQs around 150 to 160. Since IQ this high only appears in 1/10,000 people or so, it beggars coincidence to believe this represents anything but a very strong filter for IQ (or something correlated with it) in reaching that level. If you saw a group of dozens of people who were 7’0 tall on average, you’d assume it was a basketball team or some other group selected for height, not a bunch of botanists who were all very tall by coincidence.

Of the sciences, pure math is the one where innate abstract pattern ability is most strongly correlated with success, and data suggest that many of the best mathematicians in the world have innate abstract pattern recognition possessed by fewer than 1 in 10,000 people. Terry Tao's innate abstract pattern recognition ability is much rarer than 1 in 10,000, perhaps 1 in 1 million: it's extremely improbable that someone with such exceptional innate ability would by chance also be someone who would go on to do Fields Medal winning research.

Interestingly, many mathematicians are unaware of this. Terry Tao himself wrote:

A reasonable amount of intelligence is certainly a necessary (though not sufficient) condition to be a reasonable mathematician. But an exceptional amount of intelligence has almost no bearing on whether one is an exceptional mathematician.

It's not entirely clear to me how somebody as mathematically talented as Tao could miss the basic Bayesian probabilistic argument that Scott Alexander gave, which shows that Tao's own existence is very strong evidence against his claim. But two hypotheses come to mind.

Verbal reasoning ability

Like Grothendieck, like Scott Alexander, and like myself, Tao has very uneven abilities, only in an entirely different direction:

Yet at age 8 years 10 months, when he took both the SAT-M and the SAT-Verbal, Terry scored only 290 on the latter. Just 9% of college-bound male 12th-graders score 290 or less on SAT-V; a chance score is about 230. The discrepancy between being 10 points above the minimum 99th percentile on M and at the 9th percentile on V represents a gap of about 3.7 standard deviations. Clearly, Terry did far better with the mathematical reasoning items (please see the Appendix for examples) than he did reading paragraphs and answering comprehension questions about them or figuring out antonyms, verbal analogies, or sentences with missing words.

Was the "lowness" of the verbal score (excellent for one his age, of course) due to his lack of motivation on that part of the test and/or surprise at its content? A year later, while this altogether charming boy was spending four days at my home during early May of 1985, I administered another form of the SAT-V to him under the best possible conditions. His score rose to 380, which is the 31st percentile. That's a fine gain, but the M vs. V discrepancy was probably as great as before. Quite likely, on the SAT score scale his ability had risen appreciably above the 800 ceiling of SAT-M.

It's likely that principal component analysis would reveal that Tao's relatively low verbal scores reflect still lower ability on some aspect of verbal ability, which he was able to compensate for with his abstract pattern recognition ability, just as my relatively low math SAT score reflected still lower short-term memory and processing speed, which I was able to compensate for in other ways.

Aside from abstract pattern recognition ability, verbal reasoning ability is another major component of innate mathematical ability. It's reflected in performance on the analogies subtests of IQ, which like Raven's Matrices, are among the IQ subtests that correlate most strongly with the g-factor.

Broadly, the more theoretical an area of math is, the greater the role of verbal reasoning is in understanding it and doing research in it. As one would predict based on his math / verbal skewing, Tao's mathematical research is in areas of math that are relatively concrete, as opposed to theoretical. Verbal reasoning ability is also closely connected with metacognition: awareness and understanding of one's own thoughts. Tao's apparent lack of awareness of the role of his exceptional abstract reasoning ability in his mathematical success may be attributable to relatively low metacognition.

[Edit: Some commenters found the above paragraph confusing. I should clarify that the standard that I have in mind here is extremely high — I'm comparing Tao with people such as Henri Poincare, whose essays are amongst the most penetrating analyses of mathematical psychology.]

My own inclination is very much in the verbal direction, as may be evident from my posts. I used to think that it was a solely a matter of preference, but after reading the IQ literature, I realized that probably the reason that I have the preference is because verbal reasoning is what I'm best at, and we tend to enjoy what we're best at the most.

Charles Spearman, the researcher who discovered the g-factor found that the more intellectually gifted somebody is, the less correlated his or her cognitive abilities, and that when one takes this vantage point, Tao's math / verbal ability differential is not so unusual. For further detail, see Cognitive profiles of verbally and mathematically precocious students by Benbow and Minor.

I'll have more to say about the role of verbal reasoning ability in math later on.

Is this all depressing?

Another reason that Tao may have missed the evidence that his mathematical success can be in large part attributed to his exceptional abstract reasoning ability is that he might have an ugh field around the subject. Terry might find it disconcerting that the main reason that many of his colleagues at UCLA are unable to produce work that's nontrivial relative to his own is that he was born with a better brain (in some sense) than the brains of his colleagues were. Such a perspective can feel dehumanizing.

An analogy that may be offer further insight. Like Tao, Natalie Portman is talented on many different dimensions. But had she been less physically attractive than the average woman (according to the group consensus), she would not have been able to become Academy Award winning actress. Women of similar talent probably failed where she succeeded simply because they were less attractive than she is. If asked about the role of her physical appearance in her success, she would probably feel uncomfortable. One can imagine her giving an accurate answer, but one can also imagine her trying to minimize the significance of her appearance as much as possible. It might remind her of how painfully unfair life can be.

But whether or not we believe in the existence and importance of individual differences in intelligence, they're there: we can't make them go away by ignoring them. Furthermore, if not for people with unusually high intelligence, there would have been no Renaissance and no industrial revolution: Europe would still be in the dark ages, as would the rest of the world. We're very lucky to have people with cognitive abilities like Tao's, and he would have no reason to feel guilty about having being privileged. He's given back to the community through efforts such as his blog. Even if one doubts the value of theoretical research, one can still appreciate the fact that his blog serves as a proof of concept showing how elite scientists in all fields could better communicate their thinking to their research communities.

To be continued

I'll have more to say about innate later ability, but I've said enough to move on to a discussion of the connection between innate ability and mathematical ability more generally, with a view toward how it's possible to improve one's mathematical ability.

Since people's primary exposure to math is generally through school, in my next post I'll discuss math education as it's currently practiced.

My basic premise is that math education as it's currently practiced is extremely inefficient for reasons that I touched on earlier on: what goes on in math classes in practice is often very similar to studying for intelligence tests. Students and teachers are effectively trying to build abilities that are in fact fixed, rather than focusing on developing abilities that can be improved, just as I would have been if I were to have worked on making fewer "careless mistakes" in elementary school. Things don't have to be this way – math education could in principle be much more enriching.

More soon.

Growth MindsetIQ and g-factorLogic & Mathematics Skill Building

Frontpage

75

Mentioned in

69Is Scott Alexander bad at math?

8The value of learning mathematical proof

Innate Mathematical Ability

1Good_Burning_Plastic

New Comment

139 comments, sorted by

top scoring

Click to highlight new comments since: Today at 8:06 AM

Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings

[-]gjm10y240

It's likely that principal component analysis would reveal that Tao's relatively low verbal scores reflect still lower ability on some aspect of verbal ability, which he was able to compensate for with his abstract pattern recognition ability

This seems like an odd way of phrasing things, and the oddity may go deeper. As I understand it, Tao's verbal scores were still really good for an 8-year-old. So it's not like they indicate an actual mental deficit; it's just that he was really inhumanly good at mathematical reasoning versus only really good at verbal. Given that, I don't see why we should expect a "still lower ability" anywhere (I mean, beyond the trivial observation that min < average; I take it you are suggesting something more dramatic than that).

relatively low metacognition

My impression from reading TT's blog is that he has rather a lot of useful things to say about thinking techniques; see e.g. lots of the links from here. He doesn't strike me as someone with "relatively low metacognition" unless you mean "low relative to his skill as a mathematician" (in which case: well, yes, but I don't think that's an interesting observation).

I ... (read more)

8JonahS10y

I find your comment helpful insofar as it points to ways in which my article might be misunderstood, but it would be more productive to be inquisitive. No, I think that his verbal abilities are significantly above average relative to the general population, but perhaps only average relative to mathematicians as a group. Do you know principal component analysis? My point was that the SAT verbal is that surely partly a test of abstract reasoning ability of the type picked up on by Raven's Matrices, while partly being a test of a second thing, so that performance on the SAT verbal is determined by a weighted average of these two things, and that since Tao is really high on abstract reasoning ability, he must be lower on that second thing than his score would suggest if taken in isolation. Yes, these things are all relative. I added an edit to my post to clarify. For the most part, I find Tao's comments on thinking techniques and his advice sound. But there are other elite mathematicians whose understanding runs much deeper, and this is in fact highly significant, just as it's highly significant that Tao was able to score 760 on the math SAT at age 8 rather than at age 13. Do you have an alternative explanation to the two that I proposed? Surely you'll concede that there's something a priori very bizarre about the situation: Scott Alexander, who got a C- in calculus, is able to recognize a simple quantitative argument that one of the best mathematicians missed, despite the fact that Tao is much closer to the situation that Scott is analyzing than Scott is. I agree that there's some asymmetry, but I don't think that it's relevant. The point that I was getting at is more subtle. It's clearly not true that Tao and Portman were only successful because of their intelligence and looks respectively. I think that a careful reading of my paragraph will make my meaning clear, but if not, I can try to clarify.

5gjm10y

Seems plausible -- though for what it's worth I'd rate his verbal abilities substantially above those of mathematicians generally. That would be what I described as "the trivial observation that min < average" :-) and sure, I agree that whatever feature of Tao's verbal intelligence is worst has to be worse than his overall verbal intelligence, but I don't see why that's interesting enough to be worth drawing attention to. I guess your point is that if his general intelligence is so spectacularly high then to average out correctly some aspect of his verbal intelligence must be quite a lot lower than his overall verbal -- but it seems equally plausible to me that verbal SAT results just don't depend all that strongly on the kind of pattern-spotting tested by the really hard Raven matrices. I can think of several. He may have too low an opinion of his own intelligence because of the sort of weird psychological hangups that many very clever people have. He may interpret "intelligence" in a way that weights more-mathematical things less heavily (perhaps because, being so exceptional in the latter, he sees more clearly the distinction between those and other sorts of thinking). He may be a victim of Political Correctness Gone Mad and feel that he has to play down the importance of intelligence. His idea of what constitutes exceptionally high intelligence may be skewed by the fact that he is surrounded by super-smart people. He may have spent less time thinking about intelligence than Scott has (intelligence being something of a preoccupation in the rationalist community, and I suspect less so in Tao's circles). But I can't quite agree with your framing of the question: that is, I am not convinced that he has missed the argument Scott describes. Scott's argument just says: one person who's incredibly good at mathematics and incredibly good at Raven's matrices is evidence that being exceptionally good at Raven's matrices is important for being incredibly good at mathemat

9JonahS10y

I agree, there's still some effect though. The things that you list seem to me closely related to my second suggestion under "Is this all depressing?", e.g. I think that one factor that plays into "the political correctness gone mad" on this point is people want to believe that life is more fair than it actually is (for reasons overlapping somewhat with the reasons for the just-world fallacy). I would agree, if not for the fact that I'm drawing on many sources (as I described in the introduction of my last post). Some mathematicians more successful than Tao hold a contrary position. Your interpretation is very understandable. I wrote a blog post back in October 2010 implicitly expressing a position similar to your own. What started to change my thinking was point (3) of Carl's Shulman's response to my post. At the time, I was unaware of the phenomenon that he described: that performance on one task is often highly predictive of performance on an apparently unrelated task. Using a simple machine learning model, I found that amongst International Mathematics Olympiad contestants, those who went on to earn Fields medals and similar prizes had ~5x as great a priori odds relative to the average contestant, based on their IMO scores alone. The effect becomes even more pronounced when one weights prize winners by the significance of their work: for example, Perelman was one of only three perfect scorers in 1982. It doesn't necessarily agree with the inside view intuition that I've formed talking with lots of mathematicians, but the existence of a robust effect is unambiguous. I'll make a post going into detail later.

5gjm10y

There aren't a lot of mathematicians more successful than Tao. I suppose he hasn't won the Abel Prize yet. (Looking at the list of winners, it looks as if that one tends to go to older mathematicians in recognition of their lifetime's great achievements. The youngest winner was Gromov: born 1943, Abel Prize in 2009.) Could tyou name some of the mathematicians you have in mind (and, even better, point us at what they've said on the subject)?

5JonahS10y

I was referring to successful research as opposed to success at winning prizes. The connection between prizes and quality of research comes apart for a variety of reasons: arbitrary age restrictions (in both directions), ceiling effects (many prizes are awarded once a year independently of the quality of research of potential prize recipients), individual idiosyncrasies of the people on the committees that award prizes, etc. One mathematician more accomplished than Tao is Robert Langlands, known for the so-called "Langlands Program." * The program provides a long sought after vast generalization of the Artin reciprocity law (giving a conjectural answer to a 40 year old question). The Artin reciprocity law was in turn a far-reaching generalization of quadratic reciprocity, which Gauss referred to as "theorema aureum" (the golden theorem). * Three Fields medals have been awarded for work in the area, to Vladimir Drinfeld, Laurent Lafforgue and Ngô Bảo Châu. * One special case (proved by Langlands) was a crucial ingredient in Andrew Wiles' proof of Fermat's last theorem. In this essay, Langlands wrote: I know this is only a single example – it's hard to find examples of mathematicians writing about the nature of mathematical talent in the public domain altogether. But I'll try to provide more later.

7gjm10y

I wasn't meaning to imply that you define success in terms of prizes (and, for that matter, neither do I). I agree that Langlands is a more important mathematician than Tao. But that's a hell of a bar to clear. (Also, speaking of age effects, I remark that if you define mathematical success in terms of what one has achieved to date and its demonstrated influence in mathematics generally, you're inevitably going to prefer older mathematicians -- Langlands is 78 to Tao's 40ish -- and that's going to affect what biases they have affecting their ideas about intelligence, native talent, etc.) The quotation from Langlands that you give is not affirming the same thing as Tao is denying (though it's possible that Tao would in fact deny it if asked), in at least two ways. * It refers to "mathematical strength" rather than "intelligence". The assertion Tao made that you were disagreeing with was that you can be an exceptional mathematician without having exceptional intelligence, which is not the same thing as saying that you can be an exceptional mathematician without having exceptional "mathematical strength". * It refers to a single particular mathematical/physical problem. It's perfectly consistent to believe (1) that you can be an exceptional mathematician without exceptional intelligence (or exceptional "mathematical strength") but (2) that if you're going to try, you should work on something other than renormalization. For the avoidance of doubt, I won't be terribly surprised if it turns out that (say) 75% of world-class mathematicians think top 0.1% IQ is necessary to be a top 0.1% mathematician, but I'm not sure you've made much of a case yet. I'd be a little more surprised if it were 75% of world-class mathematicians who have put as much thought into the question as Tao has; I've no idea how much Langlands has actually thought about the question, but a throwaway aside in an essay about something else isn't necessarily the product of deep thought. I'll briefly

3JonahS10y

Thanks for the detailed comment. * I don't think that exceptional intelligence is either necessary or sufficient to be an exceptional mathematician. Tao's statement "But an exceptional amount of intelligence has almost no bearing on whether one is an exceptional mathematician." is a very strong statement: if he had said "plays only a moderate role in whether one is an exceptional mathematician" he would have been on much more solid ground. * I agree that the Langlands quote is by itself not strong evidence against Tao's assertion for the reasons that you give, but it's still evidence. I'm relying on many weak arguments. I'll gradually flesh them out in my sequence. * I share your intuition re: combinatorialists vs.geometers. One of my friends spent a lot of time with Chern, who struck him as being quite ordinary with respect to R, while being exceptional on a number of other dimensions. Grothendieck's self-assessment suggests that it is in fact possible to be amongst the greatest mathematicians without exceptional R. * A key point that you might be missing (certainly I did for many years) is that there just aren't many people of exceptional intelligence. Suppose that it were true that IQ is normally distributed: then the number of people of IQ 145+ would be 60x larger than the number of people of IQ 160+. Under this hypothesis, even if only 1 in 20 exceptional mathematicians had IQ 160+, that would mean that people in that range were 3x as likely as their IQ 145+ counterparts. to become exceptional mathematicians. It's been suggested that the distribution of IQ is in fact fat-tailed because of assortative mating, and this blunts the force of the aforementioned argument, but it's also true that more than 5% of exceptional mathematicians have IQ 160+: I think the actual figure is closer to 50%.

1Quill_McGee10y

It should be noted that if measured IQ is fat-tailed, this is because there is something wrong with IQ tests. IQ is defined to be normally distributed with a mean of 100 and a standard deviation of either 15 or 16 depending on which definition you're using. So if measured IQ is fat-tailed, then the tests aren't calibrated properly(of course, if your test goes all the way up to 160, it is almost inevitably miscalibrated, because there just aren't enough people to calibrate it with).

4JonahS10y

You don't want to force a normal distribution on the data. You're free to do so if you'd like, e.g. by asking takers millions of questions so as to get very fine levels of granularity, and then mapping people at the 84th percentile of "questions answered correctly" to IQ 115, people at the 98th percentile to IQ 130, etc. But what you really want is a situation where you have a (log)-linear relationship between standard deviations and other things that IQ correlates with, and if you force the data to obey a normal distribution, you'll lose this. The rationale for using a normal distribution is the central limit theorem, but that holds only when the summands are uncorrelated: assortative mating can induce correlations between e.g. having gene A that increases IQ and having gene B that increases IQ.

1Lumifer10y

Could you expand on this point? I am not sure I follow it.

1JonahS10y

Say that you have a function f: rawScores ---> percentiles and you want to compose it with a function g: percentiles ---> IQ scores so that log(g(f(x))) is as correlated with things that you care about other than IQ as much as possible (income, the log odds ratio of winning a Fields medal, etc.). The default choice for g would be the function that takes a percentile to the associated standard deviation under a normal distribution. I'm claiming that the best choice for g is probably instead a function that takes a percentile to the associated standard deviation under a distribution that has fatter tails than the normal distribution. The intuition is: Measures of the practical significance of IQ are plausibly best modeled as a weighted average of many individual genes that increase IQ. If people had been mating with randomly selected members of the opposite sex, the probabilities of getting two such genes would be independent. But in practice, people (weakly) tend to marry people of intelligence similar to their own (link), inducing a positive correlation between the respective probabilities of a child getting two different genes that contribute to IQ.

1Lumifer10y

First question: do you actually care about correlation (given that it's a linear metric) or do you mean some tight dependency, not necessarily linear? Second question: if that is the case, don't you want your function g to produce a distribution shaped similarly to the "thing you care about"? If that thing-you-care-about is distributed normally, you would prefer g to generate a normal(-looking) distribution, if it's distributed, say, as chi-squared, you would prefer g to give you a chi-squared shape, etc...? That's an iffy approach. Take, say, income (as a measure of the practical significance of IQ) -- are you saying income is best modeled as a weighted average of many IQ-related genes? You need the concept (and the link) of IQ to identify these genes to start with, but then you want to throw IQ out and go straight from genes to "practical" outcomes. I agree that assortative mating would lead to a fat-tailed distribution, but your original goal was make IQ correlate with "things you care about" and for that purpose the fat tails are not particularly relevant.

1JonahS10y

If g(y) is monotonic , then the degree to which there's a right dependency is independent of g(y), which is just a change of coordinates. I do want to chose g(y) maximize the degree to which the dependency is a linear one. Yes, this is true and a good point, though the distribution of "the thing we care about" will vary from thing to thing, and I think that if we have to used a fixed distribution for IQ that's uniform over all of them, the log of a fat-tailed distribution is probably the best choice. Here I'm just adopting an Occamistic approach – I don't have high confidence – I'm just using a linear model because it's the simplest possible function from genes to outcomes that are correlated with IQ. Feel free to suggest an alternative. Suppose, hypothetically, that human brains were such that IQ was capped at 145 by present day standards (e.g. because unbeknownst to us babies with IQ above that threshold died in childbirth for some reason having to do with IQ genes) . Then if we were to choose g(y) to get a normal distribution, it would look like the correlation between IQ and real world outcomes vanishes after 145, whereas the actual situation would be that the people who scored above 144 have essentially the same genetic composition (with respect to IQ) as the people who scored 144, so that "IQ doesn't yield returns past 145" would be connotatively misleading. I'm saying that defining IQ so that it's normally distributed has a similar (though much smaller) connotatively distortionary effect similar to this one.

1Lumifer10y

In your hypothetical there would be a lot of warning signs -- for example all IQs above 145 would be random, that is, re-testing IQs above 145 would produce a random draw from the appropriate distribution tail. And I suspect that it should be possible to figure out real-world distributions (the fatness of the tails, in particular), by looking at raw, non-normalized test scores.

1JonahS10y

Yes, you and I are on the same page, I was just saying that IQ shouldn't be defined to be normally distributed.

0dxu10y

Would you characterize this post as a reasonable description of what you're talking about in your discussion of "R"?

0gjm10y

Yes, that's the guts of it.

2MuonManLaserJab10y

Is this just a "screw you"? How about: Terence was telling a polite white lie of the sort he probably often tells. Politeness is an easier guess than "poor metacognition".

[-][anonymous]10y110

I'm going to relay an example of two apparently-different types of pattern-matching mathematical ability that apparently don't always come together from my life.

Despite the username and despite currently working on cell biology, I very nearly got a double major in astronomy in college. In high school I absolutely hated and was not good at calculus. Figuring out how to integrate anything more complicated than a basic polynomial would trip me up something fierce. Actually taking lots of astronomy and physics classes in college rescued my esteem for the subject, if not my ability to do it quickly and easily.

Throughout my astronomy and astrophysics classes I would repeatedly find it quite intuitive to figure out exactly what needed to be calculated and create the correct expressions quite fast and then trip up on doing the actual calculus while many other people would do the calculus right but not know what to actually calculate.

An example that sticks out in my mind: on a homework problem we were to estimate the fraction of the excess heat being given off by Saturn that could be accounted for by the fact that its surface is depleted in helium, presumably due to it sinking down ... (read more)

1dxu10y

It sounds to me (without any evidence, mind) that your pattern-matching ability seems to be more in the "visual" category (physical problems, etc.), and your friends' abilities are more in the "abstract" category (symbol and expression manipulation, etc.).

0[anonymous]10y

It seems to me that even within biology (as it is currently taught) there are clear distinctions of skills/mental habits between specializations. Also, there are 'tribes' like (classic) naturalists (who don't rely on molecular&genetic studies much) and 'general biologists' (who do), which makes the s/mh differences harder to visualise. For example, i would expect that a field botanist should would be able to see patterns in pictures (of grouping, spacing, geometrical transformation) better than a biotechnologist, given equal training, because visual recognition of patterns is vital in describing habitats. But i would expect the biotechnologist to hold more steps in mind if they are asked to analyze a time sequence of events, and so be better at patterns that are, well, cascading. I would also expect the botanist (and even more so, a zoologist) to consider a pattern shown inside a non-rectangle field to be a view of something whole, not disjointed, if there are interconnections, the upper half is different from the lower half or the whole pattern is radially oriented, and the field itself is either radially symmetrical or at least oblong. Simply because we saw so much cross-sections in the course of our studies, and the first and most recognizable feature of a high taxon is... body plan. That last might be easily manipulated by priming, of course, and i don't have evidence one way or the other. What is your experience?

[-]JoshuaZ10y80

Furthermore, if not for people with unusually high intelligence, there would have been no Renaissance and no industrial revolution: Europe would still be in the dark ages, as would the rest of the world.

I'm not sure about this: lots of humans can make small incremental progress. For every Isaac Newton or Terry Tao there's a 10 or 15 people who are a few years behind them.

If this is in fact true then there is I think a decent question here if the Great Filter is partially the presence of geniuses or people much smarter than the norm for the species.. It... (read more)

9[anonymous]10y

Corollary: only the fastest get noticed, not those that would've managed it a little later. Thus we get a selection effect by which we automatically attribute things to the best/fastest/whatever and don't get to see who else could do it.

4JoshuaZ10y

That definitely seems to be part of what is going on. Poincare and Hilbert were both working in very similar directions to Einstein when he came up with Special Relativity. On the other hand, in both those cases, Poincare and Hilbert were both extremely smart. On the other how much does this end up mattering? Maybe Jonah's comment is still essentially correct because the 10 or 15 people a few years behind are still people of unusually high intelligence just not as high as the very top people?

0Douglas_Knight10y

What about Hilbert and special relativity? As for Poincare, I say that he published a full theory of special relativity in 1905. We only give Einstein credit because he used it to get general relativity. He used it, but otherwise it was pretty much as ignored as Poincare's.

1JonahS10y

I don't have any knowledge of the history here, but my friend Laurens Gunnarsen (PhD in mathematical physics from University of Chicago) wrote in his (very favorable) review of Poincare's The Value of Science: I know that you may have similar background (I still don't know who you are IRL), but thought I'd point that out (though it's completely tangential to the main thread of conversation).

2Douglas_Knight10y

What is that a response to? my claim that Poincaré beat Einstein? That's not a relevant credential, and even if it were, I would not be moved by the claim unless it were a lot more precise. He might simply mean that Poincare took several papers over several years, while Einstein got it right in one try. For Joshua's purpose, priority disputes are not important. Most people who reject Poincaré's 1905 paper as a complete theory accept his 1906 paper as a complete theory not influenced by Einstein. In fact, I think that the whole concept of priority disputes is idiotic. Time is a crude proxy for influence. Columbus discovered America because it remained discovered. He changed history. Which leads to my last sentence: neither Einstein nor Poincaré's papers on special relativity had any appreciable effect. They were considered minor commentary on Maxwell's equations. The English considered them a cleaner version of FitzGerald's theory of the aether. France was not interested in special relativity until after WW2. The Germans were more enthusiastic, but that might have been some kind of (extended) nationalism, not really a different comprehension. I suppose that LG might mean that Poincaré's theory was mathematically equivalent, but philosophically off, like the English theory I mentioned above. But that English theory claimed to be Einstein's theory. Philosophical influences are difficult to follow, let alone predict.

1JonahS10y

Yes Not only does he have very deep subject matter knowledge, he's also studied the history in detail (as comes across to some degree in his Amazon review). I don't know what he had in mind, it's possible that you and he are on the same page, I just thought I'd point you to the review because it seemed to be in some tension with your claim. As for the rest of it, I don't have comments right now –I was responding specifically to the Einstein / Poincare thing.

5Epictetus10y

Carl Friedrich Gauss illustrates this quite well. He kept a lot of his mathematical discoveries to himself. When they went through his private papers after his death it was found that he'd discovered things years or even decades (or centuries) before anyone else published them. It's a matter of speculation how much farther math would have advanced had Gauss bothered to publish all his work.

4CronoDAS10y

In the case of Isaac Newton, we actually got to see this happen: Newton invented calculus several years before Leibniz's independent re-invention, but Newton didn't bother publishing anything about it until after he learned that Leibniz was trying to take credit for the same work Newton had already did.

0eternal_neophyte10y

"lots of humans can make small incremental progress" You could easily imagine that the contribution each sub-genius makes is only appreciated or assimilated in part, since it's easier to derive trivial results from powerful theorems than to construct proofs of powerful theorems from trivial results. The problem is gathering seemingly disparate and disconnected pieces of knowledge together in a single mind and linking them into a coherent whole, and a genius who produced many of these bits of knowledge by himself is in a much better position to do this than somebody who has to learn everything from external sources, struggling against the inadequacy of memory for learned material althewhile. So the "minor" contributions are lost to time simply because they're not sufficiently important to be studied widely.

[-]slicko10y70

One thing that kept nagging at me while reading this post is my own experience with taking the SAT's back in grade 11.

I don't remember my score exactly on the verbal section, but it was something like 590. Now, I've always had a noticeably above average command of language and verbal reasoning in my native tongue (based on academic feedback + my own observations), but this is obviously not reflected in the above score.

However, this is explained in my case by the fact that I only really began learning English in grade 10 (I only knew basic words from being ... (read more)

[-]James_Miller10y70

Furthermore, if not for people with unusually high intelligence, there would have been no ... industrial revolution

Is this true? Certainly you needed lots of people with IQ>100, but would the industrial revolution have happened if, say, 130 was the highest possible human IQ?

8JonahS10y

I'm pretty sure that it wouldn't have, though I don't know enough about the contextual particulars of the industrial revolution to be extremely confident. I think that studying the biographies of the inventors (to the extent that information is available) would show them all to be of IQ > 130. One could argue that counterfactually their less smart peers would have gotten there later on. There are reasons to think that if this is the case, the lag would have been very long, which I'll flesh out later on in my sequence of posts.

0DanArmak10y

And if you believe in the Flynn effect, and assuming it operated for at least a while before people started measuring IQ, the IQ 130 people of the Industrial Revolution would have a much lower measured IQ today.

5Houshalter10y

Does the Flynn effect affect the number of geniuses, or just the average IQ?

[-]Kaj_Sotala10y70

Out of curiosity, what is the correct answer to the example Raven's item? One of the answer candidates popped out to me immediately as the most likely one, and I'm interested to know whether that's a sign of me having superior pattern recognition ability or whether a part of me just wants to believe that.

[-]Vaniver10y160

The most plausible pattern for that one is exclusive or; an element is only in the third item if it is in exactly one of the preceding two items.

[-]gwillen10y180

That's interesting! I got the same answer but I visualized it differently. (Imagine, for each possible subpattern, i.e. "plus shape" or "dots", considering which items it appears in. In each case the answer is four, forming a rectangle. Two of the rectangles should extend into the ninth item, the one we're looking for.)

5Kindly10y

This is a better answer than XOR, in a sense: it describes the pattern more narrowly. If the "true pattern" were XOR, it would be possible to have a shape or subpattern occur 6 times (if it is missing once from each row and column, e.g. if it is present everywhere except in one of the diagonals). Since this does not occur for any of the six shapes, this provides some evidence that XOR is not the "true pattern". (Similarly, this is very strong evidence that "just have 4 of each shape" is not the true pattern: there are 126 ways to place a shape in 4 cells, and only 9 of them make a rectangle shape. The case against XOR, where we notice that only 9 of the 15 XOR patterns are used, is much weaker, but I still believe it.) Of course, if the goal is to just solve this particular problem, then any method works. But if we were studying the appearance of many matrices with this pattern, then you would get twice as many research points as anyone else :)

4gjm10y

The relationship between this approach and the XOR approach is interesting, I think. Thinking in XOR terms requires fancier mental infrastructure -- you need to have seen something like the idea of XOR before, and to be able to notice slightly subtle relationships between different parts of the figure. On the other hand, spotting that particular features tend to occur in rectangles involves spotting simpler things but paying more global attention to the whole figure. It feels like these play to different aspects of cognitive ability; spotting complicated patterns versus spotting large ones, so to speak. I guess the latter is closely related to working memory size, which I know is generally thought to be a large contributor to measured IQ. The former seems like an important aspect of intelligence too, and strikes me as more likely to be trainable than working memory size. (I did it with XOR.)

4JRMayne10y

I did it even more simply than that: Count things. Most have four iterations. Some have three iterations. The ones with three, make four. Less than 10 seconds for me. Same answer as the rest of everyone.

2SilentCal10y

I did it this way too. I can't help feeling like the xor way is smarter.

2Curiouskid10y

This is how I did it. My first instinct was to decompose the problem into the shapes {dots, circles, diamonds, square, +, X} and then plot which cells the shapes appear in. It's pretty easy to see the rectangles after that. Though, I didn't make the connection to XOR.

1MC_Escherichia10y

That's also interesting... I think the two ways of looking at it are equivalent, i.e. any pattern that satisfies one should also satisfy the other. (Only because the XOR pattern works both vertically and horizontally.)

0passive_fist10y

The way I solved the problem hasn't been mentioned here by anyone, which is slightly bugging me out. The way I solved it was looking at the whole puzzle as a single picture. The two bottom rows (except for the middle column) have pluses. Thus the solution must have a plus. The two right columns (except for the middle row - a transposed pattern from the previous pattern) have squares; the solution must have a square. There's only two answers with both a square and a plus; I picked the one that seemed most intuitively correct.

0Capla10y

Similarly, I go the same answer, but only by process of elimination. I knew it didn't have dots, I knew it didn't have a diamond, I knew it didn't have an x, by just extrapolating from the "cut offs" in the problem. That left me with 2, but it felt...wrong. It didn't feel intuitively right. If I had to pick on without thinking about it, number 2's the last one I'd pick. I only understand the pattern in a cohesive way from looking at the comments. Now it makes sense, instead of being deduced from bits of dis-unified information. Do I know my IQ now?

0somervta10y

I got the four, but not the rectangle - I just noticed that two elements only appeared three times.

0ahbwramc10y

Also how I did it. FWIW I know it took me more than a minute, but definitely less than five.

4SarahNibs10y

I thought about the pattern completely differently: every element is present in a 2x2 subarray.

1Error10y

Possibly of interest: I worked out the correct answer in a minute or so, but wasn't sure it was correct until I identified it as an exclusive or pattern, which I didn't figure out until after I had the answer. I note that the missing piece fits a xor pattern both across and down. I'm trying to figure out if that has to happen -- that is, if the first two rows are xor across, and the first two columns are xor down, and the missing piece fits xor in at least one direction, is it required to also fit xor in the other direction?

3Vaniver10y

That is: A⊕B=C (1) D⊕E=F (2) G⊕H=I (3) and A⊕D=G (4) B⊕E=H (5) We want to know if it is true that: C⊕F=I We begin with our goal, and substitute out C and F using (1) and (2): (A⊕B)⊕(D⊕E)=I Now we ask Wikipedia if ⊕ is associative and commutative, and the answer is yes, allowing us to rearrange that as (this is actually multiple steps, condensed): (A⊕D)⊕(B⊕E)=I Now we substitute using (4) and (5): G⊕H=I This is (3), and thus we have our proof. (Perhaps a more natural way is to start at (3) and work forward to our desired formula, but I like working backwards.) As a side point, I believe it is the case that most (all?) Raven's patterns are applied both horizontally and vertically.

6gjm10y

I think the proof is simplified by the observation that (+ meaning XOR) a+b=c is the same as a+b+c=0. So if all rows have the XOR property, we find that the XOR of all entries is 0. If two columns have the XOR property, the XOR of their entries is 0, leaving 0 for the XOR of the entries in the last column, and we're done.

0Vaniver10y

Agreed; my proof doesn't make use of the fact that C⊕C=0, and if you use that fact you get there quicker.

1JonahS10y

The actual Advanced Progressive Matrices test isn't in the public domain, but the most difficult items on clones are sometimes not "what comes next?" type items at all, but instead involve picking an item that completes the pattern in a broader sense. For example, I came across one where the pattern can only be seen by identifying opposite edges and viewing the grid as a torus.

1Vaniver10y

If you mean what I think you mean by a torus, that will maintain the vertical and horizontal symmetry. The claim I am confident in is that I don't think any Raven's test has two potential answers, one of which is more sensible if you perceive the pattern horizontally and another of which is more sensible if you perceive the pattern vertically. I am not sure whether that is accomplished by there being two equally reasonably concluding items, one of which is not included in the potential answer set, or by there never being two equally reasonable concluding items in the set of all possible items. The weaker claim, that is mostly speculation, is that the description of the pattern is the same both ways. For example, consider this possibility: 1 0 1 1 0 1 1 0 ? The answer is obviously 1, but is it because it's an xor, adding, or multiplication? The first two work horizontally but not vertically, and the latter only works vertically. I don't think there are many (any?) test patterns that look like that.

1RolfAndreassen10y

Yep, I also got this.

4Luke_A_Somers10y

I'm pretty sure it's 2 (same as Vaniver, gwillen, and Alicorn). Was that what popped out at you? It didn't take me less than 10 seconds to come up with this (I'd be surprised if it was less than 20 or more than 40 to find it and check, but I didn't check the clock). I tried to figure out the pattern without priming by looking at the possible answers, so there wasn't even really a chance to have the right answer pop out in this fashion. ETA: I have taken Raven's Matrices before, so I was ready.

2Kaj_Sotala10y

Nope: I got the fourth one. Guess it was just my brain playing tricks at me, then. :) (I tried to do it using basically just unthinking pattern recognition, looking at the sequence of patterns as a sequence of movement: somehow, using that criteria, the fourth one seemed to display "the most similar kind of motion" as compared to the above examples, even though a more conscious analysis suggested that it seemed to be breaking some of the rules of the above sequences, and I couldn't come up with any verbal summary of the rule. But it still just felt so right somehow.)

1Ishaan10y

I, too, tend towards mentally overlaying the tiles and looking for movement-patterns as I jump from one tile to another. In this case, I saw the middle row as a flash of "fire" that burned away some of the first row, and what remained was the content of the third row. (And it worked with columns too, which is how I knew that this was the correct visualization). What do you think about this? http://www.pnas.org/content/100/19/11163/F2.medium.gif Psychologists make a distinction between that sort of fuzzy similarity judgement and rule-based analytical reasoning (and the social/cultural factors that predispose people to one or the other). They're both valid ways to think about things in different contexts, but Raven's matrices are definitely rule based and you should probably avoid fuzzy holistic reasoning when trying to solve them correctly. (In the flower example, one is the holistic grouping and the other is the rule-based grouping)

0AshwinV10y

I got 6 as the answer, basing it on 1. presence of inner circle 2. outer box apparently following a pattern. But there's a high chance i'm privileging my observations.

0nyralech10y

You could also do a row-wise XOR on every feature and get 2. Which for me seemed like a pretty obvious solution to me so I went with it.

3Alicorn10y

V guvax vg'f ahzore gjb. Va rnpu pbyhza, gur funcr ba gbc trgf pebffcvrprf nqqrq naq vgf pbearef erzbirq, gura unf gur pbearef erghearq, xrrcf gur pebffcvrprf, naq ybfrf vgf zvqqyr.

2somervta10y

Huh. I got the same answer, but a different way. Rnpu vgrz vf znqr hc bs gur cerfrapr be nofrapr bs bar bs fvk onfvp ryrzragf. Rnpu ryrzrag nccrnef sbhe gvzrf, rkprcg gubfr gjb.

0Magnap10y

I got the same answer in a third way. Gur ynfg vgrz va n ebj vf znqr sebz rirelguvat va gur svefg gjb cynprf, rkprcg gung juvpu gurl unir va pbzzba. EDIT: There's a simpler name for what I did: KBE, ubevmbagnyyl.

0slicko10y

What code or syntax is this?

1Alicorn10y

It's rot-13.

1Bayeslisk10y

Oh, good. I got this too. With XOR. Contrary to other repliers, it seems to me like XOR is a simpler primitive than "the presence/absence of shapes forms a rectangle". It's more easily generalizable and doesn't rely on the existence of other patterns. As a cute curiosity, by the way, the XOR-ing works both vertically and horizontally.

1Good_Burning_Plastic10y

I did it with horizontal XOR, and I didn't notice the vertical XOR or the rectangles (which, if you think about it, are a consequence of the two XORs) until I read the comments.

0Douglas_Knight10y

The rectangle pattern is more complicated than the horizontal XOR pattern. But the rectangle pattern is the full pattern and the horizontal XOR isn't. The full pattern is the combination of both horizontal and vertical XOR patterns. You can get the answer without seeing the full pattern, just seeing the horizontal XOR pattern. The full pattern, either in rectangle form or both XORs doesn't help you get the answer, but it is useful check.

1JonahS10y

I've never had the experience of thinking that a saw the pattern and being wrong. Most Less Wrong readers' performance on Raven's Matrices would be between 2 SD and 3 SD above the mean, and I'd guess that the threshold for seeing the pattern in this particular item is in the same range. Rapidity with which one sees the answer probably gives incremental predictive power, but I'd guess that the improvement in predictive power would be much less than the improvement coming from testing untimed performance on more difficult items.

4Vaniver10y

We asked people to take a Raven's Matrices IQ test on previous surveys, like the 2012 survey. According to one of my old comments, LWers with positive karma averaged 127 on the test, somewhat below 2 SDs above the mean. I suspect that's inflated by nonresponse. There were questions about whether or not the Raven's was a good IQ test to be using, as many people thought the version hosted on iqtest.dk underestimated their IQ, and it was not included on later surveys.

3JonahS10y

I'm pretty sure that the the issue is with the conversion between performance on the iqtest.dk test and score. My best guess is that they're determining percentiles relative to other test takers, and that people who spend time taking IQ tests online are unrepresentatively high IQ.

1Vaniver10y

I think this is likely; I seem to recall iqtest.dk saying something to that effect. Given the various reporting biases involved, though, I'm unwilling to jump immediately to that as a conclusion. I recall the Raven's numbers being lower than what you would expect given the SAT numbers, but being closer to the SAT numbers than the self-reported IQ numbers, which were higher than you would expect from the SAT numbers. That is, even if I agree with your prior that LWers do better on Raven's than on other tests, observing LWers doing worse on a Raven's test than other tests should reduce my confidence in that, rather than me just using the prior to adjust the evidence to agree with it. (Administering a properly normed test, of course, would screen off the improperly normed test.)

1slicko10y

I got the answer in under 2 minutes (didn't time it exactly). However, when I first identified my answer candidate (answer 2), it was probably about two thirds of the way in. I got the correct answer by going across at first, but then spent additional time double checking my work using columns, and then double checking my answer before "committing". I've taken a couple of online Raven's Matrices type tests in the past, but that was a while ago, so I don't believe memory played too much of a role. However, I seem to have internalized the idea that IQ tests are trying to bait you with obvious answers, and as a result, I end up taking too long double checking my work. I suppose the only way to get over this lack of confidence in my intuition is with practice, but I'm wary of diluting the feedback I get from the occasional IQ test due to the 'practice effect'. It's a bit of a catch-22. Any thoughts would be appreciated.

2IlyaShpitser10y

Don't worry about IQ tests, just learn stuff you like, or be more like people that inspire you.

2JonahS10y

What are your goals?

1slicko10y

The replies to my query suggest a bit of concern that I'm be placing too much value on IQ tests, which to be honest is not quite true. I've never actually taken a formal IQ test and don't actually know my IQ score. It's really not a big concern to me, though I do believe I'm smarter than average, but then again, most people think that too. However, to answer your question,it's just my personality - I like to optimize stuff. It doesn't matter what it is, if I recognize that there's a slightly more efficient way to do something, I want to learn it and do it better. It can be as simple as someone throwing a crumbled paper into a recycling bin from a few feet away, if I notice someone is able to do that slightly more efficiently than the way I'm doing it and with better results, then I get really curious and determined to figure out how to optimize my own shots. So, along that same thread, I noticed inefficiencies in my IQ test taking skills (as I outlined in my original question), which prompted me to query you guys for any tips for improvement. And in response to shminux and Ilya's concerns, this personality trait of mine is actually quite healthy and a valued asset, it's the reason why I did well academically and am doing well in my career, so nothing to worry about!

1JonahS10y

... but a key point of my post is that context-free abstract pattern recognition ability is innate and can't be learned :-). You can learn how to answer standard Raven's matrices type questions, by learning patterns used to construct the items, but the skills built aren't transferable – if given a different kind of test of context-free abstract pattern recognition ability, you would do no better than you would now. It is possible to improve a great deal as a mathematical thinker, but trying to build this sort of skill is not the way to do it.

1emr10y

"Context-free abstract pattern recognition" can be partially resolved into more legible subcomponents, some of which can be learned, and some of which can't. So working memory is one such component, and is often theorized as a big pathway for (intuitively defined) general human intelligence. It doesn't look you can train working memory in a way that generalizes to increased performance on all tasks that involve working memory (although there's some controversy about this). And as with other traits, increased performance on formal measurements of working memory might not translate to the real-world outcomes associated with higher untrained working memory. At the same time, it seems that the universe must come packaged with a distribution over patterns, and so learning a few common patterns might transfer fairly well. The Raven pattern is XOR, a basic boolean function. The continued fraction is self-similarity, which is an interesting pattern (meta-pattern?), because while people already recognize trivial self-similarity (invariance, repetition), it look like people can be successfully taught to look for more complicated recurrences in math and CS classes.

1slicko10y

I appreciate your response, but I think you're forgetting my original question. I got the answer correctly and in under 2 minutes. I saw the pattern relatively effortlessly, but was only inquiring as to how to optimize the speed by fixing my "hesitation" to commit to the answer until I've double-checked it and ruled out any bait answers as well.

1Nornagest10y

What are you trying to buy yourself by getting better at Raven's matrices?

4slicko10y

Not buying anything, just trying to satisfy my desire to optimize any skill I have (Raven's matrices, crumbled paper basketball, driving, how to hold a pen, or any other skill). See my previous answers to JonahSinick for more details.

1Shmi10y

Echoing Ilya here. IQ tests are a rough guide of what's possible to achieve, not a predictor of success and satisfaction in life. Like height is a rough guide of what's possible to achieve in basketball. If you are 5'10", NBA is probably not for you. If your IQ tests keep returning under 120, you will probably not be an MIT prof. Unless you have some exceptional abilities not captured by these simple tests. Find something at you enjoy doing AND are very good at, and work on it. It'll pay.

0slicko10y

See my response to JonahSinick below

[-]ahbwramc10y40

Any more of this sequence forthcoming? I was looking forward to it continuing.

3JonahS10y

Yes, thanks for your interest. It's a nudge for me getting around to it sooner rather than later :-).

0grahampeterson10y

Seconded. Super important discussion and really thoughtful.

[-]emr10y30

Outliers are interesting, but I'm not sure they are often useful examples. I suspect the focus on outliers is more due to a certain insecurity among specialists, which is exactly the last thing 99.9% of the people struggling to understand or enjoy mathematics need further exposure to.

Perhaps within mathematics, progress really is so dominated by the elite that it seems natural to worry so much about elites. I don't know either way. But in most other fields, and in the everyday strength of society, there seems to be a decent potential from moving everyone ... (read more)

0JonahS10y

Thanks for your comment. I'll be addressing these things in later posts.

[-]komponisto10y30

Very interesting, thanks!

I'll have more to say about the role of verbal reasoning ability in math later on

When you do, I hope you'll mention Paul Halmos, one of my favorite mathematicians (and the author, among many other things, of Naive Set Theory, which is on the MIRI reading list), who famously began his autobiography with the sentence "I like words more than numbers, and I always did."

People who are able to pick the correct choice at all can usually do so within 2 minutes – the questions have the character "either you see it or y

... (read more)

7Shmi10y

This is an out-of-context sample from something like iqtest.dk, which builds up from easy examples to harder once over 30 min or so. If you go through the complete test, by the time you hit this example you are well ready for XOR-type patterns, so it would likely take you only seconds.

2JonahS10y

That's very interesting to me – thanks for sharing. Thanks for pointing out a possible alternative explanation. Can you elaborate? I think that I might understand what you're saying, but I'm not sure. Are you saying that UCLA math professors would be considered to be exceptional mathematicians but not exceptionally intelligent? It's not clear to me that this is the case – you seem to be breaking symmetry by interpreting his two uses of 'exceptional' in different ways. UCLA math professors are as a group more intelligent than UCLA math grad students, who are in turn as a group more intelligent than UCLA math majors. His remarks in the article that I linked suggests that he adheres to the threshold theory – that after a certain point intelligence doesn't yield incremental returns. I think that this is wrong whatever reference class one is using.

4komponisto10y

I think what Tao means is something like: among the total population of those intelligent enough to eventually become senior faculty at a UCLA-level department, variables other than intelligence are much better predictors of (the binary variable of) whether a given individual achieves (at least) that level of status (as opposed to, say, the level of more typical state universities). This is not inconsistent with intelligence being the best predictor of Tao-like status conditional upon UCLA-level status. In terms of intelligence, ordinary universities might contain a large percentage of could-have-been-UCLA's even if UCLA-level places contain only a small number of could-have-been-Tao's. I also suspect you and Tao (or at least, his public "voice" as reflected in his writings) may disagree somewhat about the relative contribution to mathematics of Tao-level and merely-UCLA-level mathematicians.

[-]John_Maxwell10y30

Tao's apparent lack of awareness of the role of his exceptional abstract reasoning ability in his mathematical success may be attributable to relatively low metacognition. (I should apologize to Tao here – it wasn't

Looks like you left an unfinished sentence here?

Tao's blog looks rather metacognitive to me, BTW.

1JonahS10y

Yeah, I was going to apologize for analyzing his psychology based on data from his childhood that was made public before he was at an age to give informed consent, but I decided not to because I also didn't want to presume that Tao would be bothered. I cut the unfinished sentence. Yes, I was comparing him to people like Poincare, etc. and added an edit to this effect in response to your comment and gjm's.

[-]Houshalter10y20

A long time ago I read something about a computer science teacher that had trouble teaching people how to program. Some people "just got it" and others just couldn't get it.

He tried giving a test beforehand to predict who would succeed and who would fail. He found that a few questions highly correlated with ability, even though they had nothing to do with programming. If I remember correctly, they involved the ability to step through the state of a system through time. Which is basically what programming is.

That doesn't necessarily imply that pro... (read more)

1Nornagest10y

I see an article every six months or so claiming something like this, though the libertarian angle is a new twist -- the usual claim is that conservatism implies an authoritarian personality. Every time I've bothered to look into one in any depth the data has turned out to be exceptionally weak, or confounded in grossly, painfully obvious ways (e.g. by failing to control for age or income). This is flattering to a different demographic, but I'm no less skeptical.

[-]common_law10y20

What's your basis for concluding that verbal-reasoning ability is an important component of mathematical ability—particularly important in more theoretical areas of math?

The research that I recall showed little influence of verbal reasoning on high-level math ability, verbal ability certainly being correlated with math ability but the correlation almost entirely accounted for by g (or R). There's some evidence that spatio-visual ability, rather unimportant for mathematical literacy (as measured by SAT-M, GRE-Q), becomes significant at higher levels of ach... (read more)

[-]johnswentworth10y20

When we're talking about innate intelligence like pattern recognition, is it mainly shaped by early development and fixed later on, or is it malleable with the right drugs?

Even more to the point, if it's the latter, does anybody know which drugs?

[-]Error10y20

Anecdote of no consequence: I halted at the Raven's Matrix until I solved it, and halted again at the math problem until I'd at least given it a go (couldn't figure it out after a couple minutes). Where's the truck?

4Luke_A_Somers10y

Well, I rather quickly identified the straightforward algebraic way of solving it. x = 1 + 1/y y = 2 + 1/y yy - 2y -1 = 0 Having reduced it to the quadratic formula and a substitution, and lacking a pen and paper, I did not pursue further at the time. Now I'm curious. Let's add 2 to complete the square... yy - 2y + 1= 2 = (y-1)(y-1) y = 1 +/- √2 Since X is 1 less than y, these yield X = +/- √2. I don't find this obvious, even in retrospect.

3ESRogs10y

If you set up the equations slightly differently it's easier to see: x = 1 + 1/(1+x) x*(1+x) = (1+x)+1 x^2+x = x +2 x^2=2

2JonahS10y

The core of the solution is recognizing that it can be reduced to a pair of algebraic equations rather than finishing off the computations. I was referring to the former in saying "could see how to answer it immediately." An extremely gifted child might also be able to solve the equations without pencil and paper, but that's a separate issue from abstract pattern recognition.

1CronoDAS10y

I solved both of them, slowly, in a sleep-deprived state. For the continued fraction, I first tried doing successive approximations to see what the answer "should" be... when I got 1.41 I figured that it was probably the square root of 2. So the next thing I did was to try squaring the expression, which wasn't exactly helpful, but it did lead me to notice that the continued fraction contained itself so I could use the algebra trick that Luke_A_Somers used.

1ahbwramc10y

I tried for maybe thirty seconds to solve it, but couldn't see anything obvious, so I decided to just truncate the fraction to see if it was close to anything I knew. From that it was clear the answer was root 2, but I still couldn't see how to solve it. Once I got into work though I had another look, and then (maybe because I knew what the answer was and could see that it was simple algebraically) I was able to come up with the above solution.

0dxu10y

I spent around twenty seconds looking at it and gave up. Then I came back fifteen minutes later, spent an additional twenty seconds looking at it and figured it out. I'm not sure what that says about my intelligence/pattern-recognition skills, but it probably says bad things about my conscientiousness.

1Curiouskid10y

In general, they're called continued fractions.

[-]Epictetus10y20

As Carl Linderholm pointed out, pattern-matching questions more properly belong to the field of parapsychology--he restricted his discussion to guessing the next number in a sequence, but the result can be readily generalized.

Satire aside, it seems to me that these Raven matrices get a lot easier to figure out once you've seen a few. At first glance I couldn't make heads or tails of the one you provided, but I went and took an online Raven matrix test and afterward that one seemed straightforward enough (in the sense that I quickly found a rule that was co... (read more)

5Douglas_Knight10y

Yes, Raven's problems do get easier when you've seen them. It exhibits a strong learning effect. People improve when retaking it more than on other IQ tests. Armstrong-Woodley claim that learning effect correlates with Flynn effect.

4JonahS10y

Intelligence seems to account for roughly 40% of the variance in the logarithms of mathematicians' research productivity, with the remainder accounted for by other innate abilities and environmental factors. This is consistent with most exceptionally intelligent mathematicians producing unremarkable math, and also (given the rarity of people with exceptional intelligence) consistent with some great mathematicians not being exceptionally intelligent. I'll write more about this later.

1Epictetus10y

Nice to know there's still hope for the rest of us.

2komponisto10y

Some of my candidates (who, perhaps not coincidentally, also happen to be among my "favorite" old-time mathematicians, in the sense of stylistic identification): * Hilbert * Weierstrass * Lie * Cantor * Noether All of these violate (what I think of as) the "math genius" stereotype in some way. None of these were considered child prodigies; in many cases they took up mathematics relatively late (Lie), had some competing interest (Cantor), or stood in contrast to a prodigy they knew (Hilbert, the prodigy being Minkowski). Expanding the scope to physicists (and in the category of "widely held cultural beliefs that are probably wrong"), I will also nominate: * Einstein whom I suspect of possessing significantly less Tao-style ability, and being more akin to the above-listed mathematicians, than is commonly assumed.

2JonahS10y

Tao's abstract pattern recognition ability would seem to mark him as an outlier amongst mathematicians of similar accomplishment, whose relatively lower abstract pattern recognition abilities are counterbalanced by other abilities (some innate and others developed).

2[anonymous]10y

I've heard a version of this proposed as an explanation for the Flynn effect - industrialized urbanized nations with standardized schooling exposing people to more and more problems of the type the IQ test contains over time.

[-]Ishaan10y10

I've always felt the working memory, and also just recall in general, was my limiting factor in doing certain kinds of math (not for lack of interest or trying). In cases where the problem is solved by understanding some underlying structure there is no particular disadvantage... but the rule-execution, manipulation of equations, substitutions, etc especially when done in the absence of conceptual understanding is really challenging.

I've got a similar cognitive profile to what you describe - ceiling verbal, above-average everything else, barely average sh... (read more)

[-]Curiouskid10y10

Thank you for writing this series Jonah. I'm don't have the time now to think deeply about this topic, so I thought I'd add to the discussion by mentioning a few related interesting anecdotes.

I doubt what made the Polgar sisters great was innate intelligence.

Another interesting anecdote is von Neumann not (initially?) appreciating the importance of higher-level programming languages:

John von Neumann, when he first heard about FORTRAN in 1954, was unimpressed and asked "why would you want more than machine language?" One of von Neumann's stud

... (read more)

3alienist10y

Given the state of computing at the time, it's possible that computer time really was more valuable then graduate student time.

3dxu10y

Their father, Laszlo Polgar, was himself a fairly strong chess player, and it is well-known that intelligence is heritable. In addition, Judit Polgar at least (I don't know about the others) was a child prodigy, implying that she had a great deal of innate ability. Furthermore, chess requires very good working memory (due to something called the touch-move rule forcing players to calculate variations mentally), and it is theorized that working memory may actually be intelligence, further supporting the "innate ability" hypothesis.

0IlyaShpitser10y

That is a very interesting anecdote about von Neumann, if true. The man was one of a kind, and it would be interesting if the need for abstraction in this domain was not clear to him just from doing a ton of math. Maybe blindness-due-to-status ("clerical work...")

[-]slicko10y00

I had the same reaction to calling it "fancy".

I got the answer fairly quick (didn't time it, but probably about a minute or two). In my head, I was thinking of subtraction, not even "cancelling out".

In a row, cell 1 minus cell 2 equaled cell 3.

I suppose that is an XOR pattern after all, but you only need knowledge of basic arithmetic to verbalize the pattern.

(edit: upon rereading my answer, I guess it's not fair to call it a subtraction only, since I'm still keeping around shapes from cell 1 or cell 2 provided they weren't subtracted. Apparently my brain is doing XOR while thinking of it as a subtraction)

[-]gjm10y00

Yup, that's about the level of fanciness. Not too bad, as you say, but I think harder to think of than four things forming a rectangle. (But maybe easier to notice, as I suggested above.)

[-][anonymous]10y00

I solved the first puzzle in the matter of minutes, yet just looking at the second one made me give up. It seems to me that there might be even more bifurcations, even within the difficulty level and similarity of presentation.

(the second term inthe equation, to me, resembles a description of loosely plated hair (of indefinite length), and in particular, of the non-spilled part; but how to describe the spilled part as a continued fraction? Sorry for the rant.)

3gjm10y

I suspect that all that shows is that you aren't used to the relevant bits of mathematics, and being confronted with unfamiliar and weird-looking notation intimidates you. There's no shame in that, and it says basically nothing about your intelligence or your natural aptitude for mathematics. (Remember that the Raven matrices are designed to have as little dependence on prior knowledge as possible; mathematical questions, almost by definition, are not.)

0slicko10y

I agree with your overall response, but your note that "weird-looking notation intimidates you" kind of surprised me. From my perspective, it's not a question of intimidation so much as it is a recognition that the question is targeting a different audience (one who knows such notation). If you encounter new notation, there is no way to derive the answer anyway by simply "facing" it head on (i.e. without being intimidated), you actually have to look up the notation and any associated information you didn't already know, which requires a higher activation energy (and enthusiasm) than trying your hand at a question with known notation.

0IlyaShpitser10y

Seconding this, weird notation makes many folks lose morale easily. I guess one watershed moment comes when, having conquered enough notation in specific cases, one realizes it's just a formal symbol pushing game in general, and then new weird looking notation doesn't cause a morale crisis. Novel math papers often just invent new notation as they go.

0slicko10y

I'm reminded of Graham's number (g notation) as an example where new notation (kind of) was invented for the purposes of a math paper. I read a riveting blog post a few months ago introducing several concepts and building up to graham's number in a very accessible read if anyone's interested: http://waitbutwhy.com/2014/11/1000000-grahams-number.html

[-]dxu10y-10

Just checking, but verbal and mathematical reasoning skills are positively correlated, right? This assertion seems to be supported by the fact that many (I'd go so far as to say nearly all) LW users have high verbal intelligence (as evidenced by the general quality of the comments here) and most of them seem to have high mathematical intelligence as well (as evidenced by the many posts on decision theory, game theory, and other fields of mathematics). If the two are correlated, do you know the coefficient of correlation?

5JonahS10y

Yes, the two are correlated. I'm surprised at not being able to find a really good reference, but doing linear regression on this dataset of SAT scores from a class of 162 high school seniors gives a correlation of 0.68 between math and verbal.

0dxu10y

Wow. A correlation coefficient of 0.68 is... actually pretty highly correlated. That's much higher than I was expecting. (I thought the correlation would be at most 0.5 or so.)

0sixes_and_sevens10y

What does an anticipated 0.5 correlation coefficient between two variables feel like?

2dxu10y

I said at most 0.5, not exactly 0.5. The latter requires a level of predictive confidence that I don't have, so if you're asking what the latter feels like, then I don't know. If you're asking what the former feels like, it basically means I didn't expect the correlation to be more than, say, the correlation between someone's SAT scores and their ACT scores.

2Douglas_Knight10y

No, the correlation between SAT and ACT is higher than the correlation between SAT-M and SAT-V. Of course it is. You should be shocked if it isn't. The small correlation between SAT and ACT in that sample is due to restriction of range. If the same sample had been polled on component scores, the M-V correlation would have been even smaller. For a larger sample, the SAT-ACT correlation is 0.9 (p5/10) [and if that's a self-selected sample of people who took both, the correlation on the whole population is probably higher]. Also from that source, SAT-M correlates 0.9 with ACT-Math, though SAT-V only correlated 0.8 with ACT-Reading and ACT-English. This book claims an M-V correlation of only 0.56, but I haven't determined what the sample was. (I find Jonah's 0.68 more plausible, but this seems like a better source.)

0sixes_and_sevens10y

That makes sense. Thank you.

2Kaj_Sotala10y

One reference that also comes to mind is this box from Deary 2001. If we assume "verbal intelligence" to correspond to the "verbal comprehension" group factor in the diagram, and "mathematical reasoning" to correspond to its "perceptual organization" factor (since perceptual organization's associated subtests of picture completion, block design, matrix reasoning, and picture arrangement sound the most similar to Raven's matrices; though "arithmetic" is in the working memory factor) then if I'm thinking about this correct, those two group factors would share 65% (100 0.86^2 0.94^2) of their variance.

[-]Flextechmgmt10y-30

Really illuminating paper here! I appreciate you sharing this. Here's what I think - innate ability is overvalued, everyone! If you hone your skills over time you will seem smarter than you are & you lose some of your shyness & inhibitions w.r.t. asserting yourself & expressing your opinion. My top grades were a 2200 on my SAT's, 31 on my ACT's, & I was an honors student in college. That being said, I don't think that correlates with intelligence. That just correlates with testing well. Isaac Newton made major contributions to his STEM care... (read more)

1Arkanj3l10y

Do you know what it's like to be stupid?

0Flextechmgmt10y

To some extent, yes.. When I'm in a lecture hall in college & the professor is talking about theoretical physics, I feel pretty stupid & I'm confused & don't really understand what's going on. So, yes, I guess I do.

Moderation Log