Thanks for writing this -- I’m very excited about people pushing back on/digging deeper re: counting arguments, simplicity arguments, and the other arguments re: scheming I discuss in the report. Indeed, despite the general emphasis I place on empirical work as the most promising source of evidence re: scheming, I also think that there’s a ton more to do to clarify and maybe debunk the more theoretical arguments people offer re: scheming – and I think playing out the dialectic further in this respect might well lead to comparatively fast progress (for all their centrality to the AI risk discourse, I think arguments re: scheming have received way too little direct attention). And if, indeed, the arguments for scheming are all bogus, this is super good news and would be an important update, at least for me, re: p(doom) overall. So overall I’m glad you’re doing this work and think this is a valuable post.
Another note up front: I don’t think this post “surveys the main arguments that have been put forward for thinking that future AIs will scheme.” In particular: both counting arguments and simplicity arguments (the two types of argument discussed in the post) assum...
Humans under selection pressure—e.g. test-takers, job-seekers, politicians—will often misrepresent themselves and their motivations to get ahead. That very basic fact that humans do this all the time seems like sufficient evidence to me to consider the hypothesis at all (though certainly not enough evidence to conclude that it's highly likely).
If I examine the causal mechanisms here, I find things like "humans seem to have have 'parameterizations' which already encode situationally activated consequentialist reasoning", and then I wonder "will AI develop similar cognition?" and then that's the whole thing I'm trying to answer to begin with.
Do you believe that AI systems won't learn to use goal-directed consequentialist reasoning even if we train them directly on outcome-based goal-directed consequentialist tasks? Or do you think we won't ever do that?
If you do think we'll do that, then that seems like all you need to raise that hypothesis into consideration. Certainly it's not the case that models always learn to value anything like what we train them to value, but it's obviously one of the hypotheses that you should be seriously considering.
I'm not sure where it was established that what's under consideration here is just deceptive alignment in pre-training. Personally, I'm most worried about deceptive alignment coming after pre-training. I'm on record as thinking that deceptive alignment is unlikely (though certainly not impossible) in purely pretrained predictive models.
I really do appreciate this being written up, but to the extent that this is intended to be a rebuttal to the sorts of counting arguments that I like, I think you would have basically no chance of passing my ITT here. From my perspective reading this post, it read to me like "I didn't understand the counting argument, therefore it doesn't make sense" which is (obviously) not very compelling to me. That being said, to give credit where credit is due, I think some people would make a more simplistic counting argument like the one you're rebutting. So I'm not saying that you're not rebutting anyone here, but you're definitely not rebutting my position.
Edit: If you're struggling to grasp the distinction I'm pointing to here, it might be worth trying this exercise pointing out where the argument in the post goes wrong in a very simple case and/or looking at Ryan's restatement of my mathematical argument.
Edit: Another point of clarification here—my objection is not that there is a "finite bitstring case" and an "infinite bitstring case" and you should be using the "infinite bitstring case". My objection is that the sort of finite bitstring analysis in this post does not yield any well-de...
Thanks for the reply. A couple remarks:
- "indifference over infinite bitstrings" is a misnomer in an important sense, because it's literally impossible to construct a normalized probability measure over infinite bitstrings that assigns equal probability to each one. What you're talking about is the length weighted measure that assigns exponentially more probability mass to shorter programs. That's definitely not an indifference principle, it's baking in substantive assumptions about what's more likely.
- I don't see why we should expect any of this reasoning about Turing machines to transfer over to neural networks at all, which is why I didn't cast the counting argument in terms of Turing machines in the post. In the past I've seen you try to run counting or simplicity arguments in terms of parameters. I don't think any of that works, but I at least take it more seriously than the Turing machine stuff.
- If we're really going to assume the Solomonoff prior here, then I may just agree with you that it's malign in Christiano's sense and could lead to scheming, but I take this to be a reductio of the idea that we can use Solomonoff as any kind of model for real world machine learning. De
"indifference over infinite bitstrings" is a misnomer in an important sense, because it's literally impossible to construct a normalized probability measure over infinite bitstrings that assigns equal probability to each one. What you're talking about is the length weighted measure that assigns exponentially more probability mass to shorter programs. That's definitely not an indifference principle, it's baking in substantive assumptions about what's more likely.
No; this reflects a misunderstanding of how the universal prior is traditionally derived in information theory. We start by assuming that we are running our UTM over code such that every time the UTM looks at a new bit in the tape, it has equal probability of being a 1 or a 0 (that's the indifference condition). That induces what's called the universal semi-measure, from which we can derive the universal prior by enforcing a halting condition. The exponential nature of the prior simply falls out of that derivation.
...I don't see why we should expect any of this reasoning about Turning machines to transfer over to neural networks at all, which is why I didn't cast the counting argument in terms of Turing machines in the pos
I'm well aware of how it's derived. I still don't think it makes sense to call that an indifference prior, precisely because enforcing an uncomputable halting requirement induces an exponentially strong bias toward short programs. But this could become a terminological point.
I think relying on an obviously incorrect formalism is much worse than relying on no formalism at all. I also don't think I'm relying on zero formalism. The literature on the frequency/spectral bias is quite rigorous, and is grounded in actual facts about how neural network architectures work.
Yes, but your original comment was presented as explaining "how to properly reason about counting arguments." Do you no longer claim that to be the case? If you do still claim that, then I maintain my objection that you yourself used hand-wavy reasoning in that comment, and it seems incorrect to present that reasoning as unusually formally supported.
Another concern I have is, I don't think you're gaining anything by formality in this thread. As I understand your argument, I think your symbols are formalizations of hand-wavy intuitions (like the ability to "decompose" a network into the given pieces; the assumption that description length is meaningfully relevant to the NN prior; assumptions about informal notions of "simplicity" being realized in a given UTM prior). If anything, I think that the formality makes things worse because it makes it harder to evaluate or critique your claims.
I also don't think I've seen an example of reasoning about deceptive alignment where I concluded that formality had helped the case, as opposed to obfuscated the case or lent the concern unearned credibility.
I think you should allocate time to devising clearer arguments, then. I am worried that lots of people are misinterpreting your arguments and then making significant life choices on the basis of their new beliefs about deceptive alignment, and I think we'd both prefer for that to not happen.
Here's another fun way to think about this—you can basically cast what's wrong here as an information theory exercise.
Problem:
Spot the step where the following argument goes wrong:
- Suppose I have a dataset of finitely many points arranged in a line. Now, suppose I fit a (reasonable) universal prior to that dataset, and compare two cases: learning a line and learning to memorize each individual datapoint.
- In the linear case, there is only one way to implement a line.
- In the memorization case, I can implement whatever I want on the other datapoints in an arbitrary way.
- Thus, since there are more ways to memorize than to learn a line, there should be greater total measure on memorization than on learning the line.
- Therefore, you'll learn to memorize each individual datapoint rather than learning to implement a line.
Solution:
By the logic of the post, step 4 is the problem, but I think step 4 is actually valid. The problem is step 2: there are actually a huge number of different ways to implement a line! Not only are there many different programs that implement the line in different ways, I can also just take the simplest program that does so and keep on adding comments or other extraneous b
From my perspective reading this post, it read to me like "I didn't understand the counting argument, therefore it doesn't make sense" which is (obviously) not very compelling to me.
I definitely appreciate how it can feel frustrating or bad when you feel that someone isn't properly engaging with your ideas. However, I also feel frustrated by this statement. Your comment seems to have a tone of indignation that Quintin and Nora weren't paying attention to what you wrote.
I myself expected you to respond to this post with some ML-specific reasoning about simplicity and measure of parameterizations, instead of your speculation about a relationship between the universal measure and inductive biases. I spoke with dozens of people about the ideas in OP's post, and none of them mentioned arguments like the one you gave. I myself have spent years in the space and am also not familiar with this particular argument about bitstrings.
(EDIT: Having read Ryan's comment, it now seems to me that you have exclusively made a simplicity argument without any counting involved, and an empirical claim about the relationship between description length of a mesa objective and the probability of...
I myself expected you to respond to this post with some ML-specific reasoning about simplicity and measure of parameterizations, instead of your speculation about a relationship between the universal measure and inductive biases. I spoke with dozens of people about the ideas in OP's post, and none of them mentioned arguments like the one you gave. I myself have spent years in the space and am also not familiar with this particular argument about bitstrings.
That probably would have been my objection had the reasoning about priors in this post been sound, but since the reasoning was unsound, I turned to the formalism to try to show why it's unsound.
If these are your real reasons for expecting deceptive alignment, that's fine, but I think you've mentioned this rather infrequently.
I think you're misunderstanding the nature of my objection. It's not that Solomonoff induction is my real reason for believing in deceptive alignment or something, it's that the reasoning in this post is mathematically unsound, and I'm using the formalism to show why. If I weren't responding to this post specifically, I probably wouldn't have brought up Solomonoff induction at all.
...This yields a perfe
Paradoxically, I think larger neural networks are more simplicity-biased.
The idea is that when you make your network larger, you increase the size of the search space and thus the number of algorithms that you're considering to include algorithms which take more computation. That reduces the relative importance of the speed prior, but increases the relative importance of the simplicity prior, because your inductive biases are still selecting from among those algorithms according to the simplest pattern that fits the data, such that you get good generalization—and in fact even better generalization because now the space of algorithms in which you're searching for the simplest one in is even larger.
Another way to think about this: if you really believe Occam's razor, then any learning algorithm generalizes exactly to the extent that it approximates a simplicity prior—thus, since we know neural networks generalize better as they get larger, they must be approximating a simplicity prior better as they do so.
This isn't a proper response to the post, but since I've occasionally used counting-style arguments in the past I think I should at least lay out some basic agree/disagree points. So:
- This post basically-correctly refutes a kinda-mediocre (though relatively-commonly-presented) version of the counting argument.
- There does exist a version of the counting argument which basically works.
- The version which works routes through compression and/or singular learning theory.
- In particular, that version would talk about "goal-slots" (i.e. general-purpose search) showing up for exactly the same reasons that neural networks are able to generalize in the overparameterized regime more generally. In other words, if you take the "counting argument for overfitting" from the post, walk through the standard singular-learning-theory-style response to that story, and then translate that response over to general-purpose search as a specific instance of compression, then you basically get the good version of the counting argument.
- Just remembered I walked through basically the good version of the counting argument in this section of What's General-Purpose Search, And Why Might We Expect To See It In Trained M
I'm pleasantly surprised that you think the post is "pretty decent."
I'm curious which parts of the Goal Realism section you find "philosophically confused," because we are trying to correct what we consider to be deep philosophical confusion fairly pervasive on LessWrong.
I recall hearing your compression argument for general-purpose search a long time ago, and it honestly seems pretty confused / clearly wrong to me. I would like to see a much more rigorous definition of "search" and why search would actually be "compressive" in the relevant sense for NN inductive biases. My current take is something like "a lot of the references to internal search on LW are just incoherent" and to the extent you can make them coherent, NNs are either actively biased away from search, or they are only biased toward "search" in ways that are totally benign.
More generally, I'm quite skeptical of the jump from any mechanistic notion of search, and the kind of grabby consequentialism that people tend to be worried about. I suspect there's a double dissociation between these things, where "mechanistic search" is almost always benign, and grabby consequentialism need not be backed by mechanistic search.
I would like to see a much more rigorous definition of "search" and why search would actually be "compressive" in the relevant sense for NN inductive biases. My current take is something like "a lot of the references to internal search on LW are just incoherent" and to the extent you can make them coherent, NNs are either actively biased away from search, or they are only biased toward "search" in ways that are totally benign.
More generally, I'm quite skeptical of the jump from any mechanistic notion of search, and the kind of grabby consequentialism that people tend to be worried about. I suspect there's a double dissociation between these things, where "mechanistic search" is almost always benign, and grabby consequentialism need not be backed by mechanistic search.
Some notes on this:
- I don't think general-purpose search is sufficiently well-understood yet to give a rigorous mechanistic definition. (Well, unless one just gives a very wrong definition.)
- Likewise, I don't think we understand either search or NN biases well enough yet to make a formal compression argument. Indeed, that sounds like a roughly-agent-foundations-complete problem.
- I'm pretty skeptical that internal general-
Some incomplete brief replies:
Huemer... indeed seems confused about all sorts of things
Sure, I was just searching for professional philosopher takes on the indifference principle, and that chapter in Paradox Lost was among the first things I found.
Separately, "reductionism as a general philosophical thesis" does not imply the thing you call "goal reductionism"
Did you see the footnote I wrote on this? I give a further argument for it.
doesn't mean the end-to-end trained system will turn out non-modular.
I looked into modularity for a bit 1.5 years ago and concluded that the concept is way too vague and seemed useless for alignment or interpretability purposes. If you have a good definition I'm open to hearing it.
There are good reasons behaviorism was abandoned in psychology, and I expect those reasons carry over to LLMs.
To me it looks like people abandoned behaviorism for pretty bad reasons. The ongoing replication crisis in psychology does not inspire confidence in that field's ability to correctly diagnose bullshit.
That said, I don't think my views depend on behaviorism being the best framework for human psychology. The case for behaviorism in the AI case is much, much stronger: the equations for an algorithm like REINFORCE or DPO directly push up the probability of some actions and push down the probability of others.
Did you see the footnote I wrote on this? I give a further argument for it.
Ah yeah, I indeed missed that the first time through. I'd still say I don't buy it, but that's a more complicated discussion, and it is at least a decent argument.
I looked into modularity for a bit 1.5 years ago and concluded that the concept is way too vague and seemed useless for alignment or interpretability purposes. If you have a good definition I'm open to hearing it.
This is another place where I'd say we don't understand it well enough to give a good formal definition or operationalization yet.
Though I'd note here, and also above w.r.t. search, that "we don't know how to give a good formal definition yet" is very different from "there is no good formal definition" or "the underlying intuitive concept is confused" or "we can't effectively study the concept at all" or "arguments which rely on this concept are necessarily wrong/uninformative". Every scientific field was pre-formal/pre-paradigmatic once.
...To me it looks like people abandoned behaviorism for pretty bad reasons. The ongoing replication crisis in psychology does not inspire confidence in that field's ability to correctly diagnose bullshit.
That
Since there are “more” possible schemers than non-schemers, the argument goes, we should expect training to produce schemers most of the time. In Carlsmith’s words:
It's important to note that the exact counting argument you quote isn't one that Carlsmith endorses, just one that he is explaning. And in fact Carlsmith specifically notes that you can't just apply something like the principle of indifference without more reasoning about the actual neural network prior.
(You mention this later in the "simplicity arguments" section, but I think this objection is sufficiently important and sufficiently missing early in the post that it is important to emphasize.)
Quoting somewhat more context:
...I start, in section 4.2, with what I call the “counting argument.” It runs as follows:
- The non-schemer model classes, here, require fairly specific goals in order to get high reward.
- By contrast, the schemer model class is compatible with a very wide range of (beyond- episode) goals, while still getting high reward (at least if we assume that the other require- ments for scheming to make sense as an instrumental strategy are in place—e.g., that the classic goal-guarding story, or some alternative
We argue against the counting argument in general (more specifically, against the presumption of a uniform prior as a "safe default" to adopt in the absence of better information). This applies to the hazy counting argument as well.
We also don't really think there's that much difference between the structure of the hazy argument and the strict one. Both are trying to introduce some form of ~uniformish prior over the outputs of a stochastic AI generating process. The strict counting argument at least has the virtue of being precise about which stochastic processes it's talking about.
If anything, having more moving parts in the causal graph responsible for producing the distribution over AI goals should make you more skeptical of assigning a uniform prior to that distribution.
I agree that you can't adopt a uniform prior. (By uniform prior, I assume you mean something like, we represent goals as functions from world states to a (real) number where the number says how good the world state is, then we take a uniform distribution over this function space. (Uniform sampling from function space is extremely, extremely cursed for analysis related reasons without imposing some additional constraints, so it's not clear uniform sampling even makes sense!))
Separately, I'm also skeptical that any serious historical arguments were actually assuming a uniform prior as opposed to trying to actual reason about the complexity/measure of various goal in terms of some fixed world model given some vague guess about the representation of this world model. This is also somewhat dubious due to assuming a goal slot, assuming a world model, and needing to guess at the representation of the world model.
(You'll note that ~all prior arguements mention terms like "complexity" and "bits".)
Of course, the "Against goal realism" and "Simplicity arguments" sections can apply here and indeed, I'm much more sympathetic to these sections than to the counting argument section which seems like a strawman as far as I can tell. (I tried to get to ground on this by communicating back and forth some with you and some with Alex Turner, but I failed, so now I'm just voicing my issues for third parties.)
I don't think this is a strawman. E.g., in How likely is deceptive alignment?, Evan Hubinger says:
...We're going to start with simplicity. Simplicity is about specifying the thing that you want in the space of all possible things. You can think about simplicity as “How much do you have to aim to hit the exact thing in the space of all possible models?” How many bits does it take to find the thing that you want in the model space? And so, as a first pass, we can understand simplicity by doing a counting argument, which is just asking, how many models are in each model class?
First, how many Christs are there? Well, I think there's essentially only one, since there's only one way for humans to be structured in exactly the same way as God. God has a particular internal structure that determines exactly the things that God wants and the way that God works, and there's really only one way to port that structure over and make the unique human that wants exactly the same stuff.Okay, how many Martin Luthers are there? Well, there's actually more than one Martin Luther (contrary to actual history) because the Martin Luthers can point to the Bible in different ways. There's a lot of different eq
(I might write a longer response later, but I thought it would be worth writing a quick response now. Cross-posted from the EA forum, and I know you've replied there, but I'm posting anyway.)
I have a few points of agreement and a few points of disagreement:
Agreements:
- The strict counting argument seems very weak as an argument for scheming, essentially for the reason you identified: it relies on a uniform prior over AI goals, which seems like a really bad model of the situation.
- The hazy counting argument—while stronger than the strict counting argument—still seems like weak evidence for scheming. One way of seeing this is, as you pointed out, to show that essentially identical arguments can be applied to deep learning in different contexts that nonetheless contradict empirical evidence.
Some points of disagreement:
- I think the title overstates the strength of the conclusion. The hazy counting argument seems weak to me but I don't think it's literally "no evidence" for the claim here: that future AIs will scheme.
- I disagree with the bottom-line conclusion: "we should assign very low credence to the spontaneous emergence of scheming in future AI systems—perhaps 0.1% or less"
- I think it's
Deep learning is strongly biased toward networks that generalize the way humans want— otherwise, it wouldn’t be economically useful.
This is NOT what the evidence supports, and super misleadingly phrased. (Either that, or it's straightup magical thinking, which is worse)
The inductive biases / simplicity biases of deep learning are poorly understood but they almost certainly don't have anything to do with what humans want, per se. (that would be basically magic) Rather, humans have gotten decent at intuiting them, such that humans can often predict how the neural network will generalize in response to such-and-such training data. i.e. human intuitive sense of simplicity is different, but not totally different, at least not always, from the actual simplicity biases at play.
Stylized abstract example: Our current AI is not generalizing in the way we wanted it to. Looking at its behavior, and our dataset, we intuit that the dataset D is narrow/nondiverse in ways Y and Z and that this could be causing the problem; we go collect more data so that our dataset is diverse in those ways, and try again, and this time it works (i.e. the AI generalizes to unseen data X). Why did this happen? Why ...
they almost certainly don't have anything to do with what humans want, per se. (that would be basically magic)
We are obviously not appealing to literal telepathy or magic. Deep learning generalizes the way we want in part because we designed the architectures to be good, in part because human brains are built on similar principles to deep learning, and in part because we share a world with our deep learning models and are exposed to similar data.
Saying we design the architectures to be good is assuming away the problem. We design the architectures to be good according to a specific set of metrics (test loss, certain downstream task performance, etc). Problems like scheming are compatible with good performance on these metrics.
I think the argument about the similarity between human brains and the deep learning leading to good/nice/moral generalization is wrong. Human brains are way more similar to other natural brains which we would not say have nice generalization (e.g. the brains of bears or human psychopaths). One would need to make the argument that deep learning has certain similarities to human brains that these malign cases lack.
I think that if you do assume a fixed goal slot and outline an overall architecture, then there are pretty good arguments for a serious probabilty of scheming.
(Though there are also plenty of bad arguments, including some that people have made in the past : ).)
That said, I'm sympathetic to some version of the "Against goal realism" argument applying to models which are sufficiently useful. As in, the first transformatively useful models won't in practice contain have internal (opaque-to-human-overseers) goals such that the traditional story for scheming doesn't apply.
(However, it's worth noting that at least some humans do seem to have internal goals and reductionism doesn't defeat this intuition. It's not super clear that the situation with humans is well described as a "goal slot", though there is pretty clearly some stuff that could be changed in a human brain that would cause them to be well described as coherantly pursue different goals. So arguing that AIs won't have internal goals in a way that could result in scheming does require noting some ways in which you're argument doesn't apply to humans. More strongly, humans can and do scheme even in cases where some overseer sele...
The current literature on scheming appears to have been inspired by Paul Christiano’s speculations about malign intelligences in Solomonoff induction
This doesn't seem right. The linked post by Paul here is about the (extremely speculative) case where consequentialist life emerges organically inside of full blown simulations (e.g. evolving from scratch) while arguments about ML models never go here.
Regardless, concerns and arguments about scheming are much older than Paul's posts on this topic.
(That said, I do think that people have made scheming style arguments based on intuitions from thinking about AIXI and the space of turing machines at various points. Though this was never very key and I don't believe these arguments are ever in reference to cases where a literal simulation evolves life.)
There is also a hazy counting argument for overfitting:
- It seems like there are “lots of ways” that a model could end up massively overfitting and still get high training performance.
- So absent some additional story about why training won’t select an overfitter, it feels like the possibility should be getting substantive weight.
While many machine learning researchers have felt the intuitive pull of this hazy overfitting argument over the years, we now have a mountain of empirical evidence that its conclusion is false. Deep learning is strongly biased toward networks that generalize the way humans want— otherwise, it wouldn’t be economically useful.
I don't know well NN history, but I have the impression good NN training is not trivial. I expect that the first attempts at NN training went bad in some way, including overfitting. So, without already knowing how to train an NN without overfitting, you'd get some overfitting in your experiments. The fact that now, after someone already poured their brain juice over finding techniques that avoid the problem, you don't get overfitting, is not evidence that you shouldn't have expected overfitting before.
The analogy with AI schemin...
Joe also discusses simplicity arguments for scheming, which suppose that schemers may be “simpler” than non-schemers, and therefore more likely to be produced by SGD.
I'm not familiar with the details of Joe's arguments, but to me the strongest argument from simplicity is not that schemers are simpler than non-schemers, it's that scheming itself is conceptually simple and instrumentally useful. So any system capable of doing useful and general cognitive work will necessarily have to at least be capable of scheming.
...We will address this question in greater detail in a future post. However, we believe that current evidence about inductive biases points against scheming for a variety of reasons. Very briefly:
- Modern deep neural networks are ensembles of shallower networks. Scheming seems to involve chains of if-then reasoning which would be hard to implement in shallow networks.
- Networks have a bias toward low frequency functions— that is, functions whose outputs change little as their inputs change. But scheming requires the AI to change its behavior dramatically (executing a treacherous turn) in response to subtle cues indicating it is not in a sandbox, and could successfully escape.
- The
I don't get how you can arrive at 0.1% for future AI systems even if NNs are biased against scheming. Humans scheme, the future AI systems trained to be capable of long if-then chains may also learn to scheme, maybe because explicitly changing biases is good for performance. Or even, what, you have <0.1% on future AI systems not using NNs?
Also, not saying "but it doesn't matter", but assuming everyone agrees that spectrally biased NN with classifier or whatever is a promising model of a safe system. Do you then propose we should not worry and just make the most advanced AI we can as fast as possible. Or it would be better to first reduce remaining uncertainty about behavior of future systems?
The exact language you use in the post is:
We therefore conclude that we should assign very low credence to the spontaneous emergence of scheming in future AI systems— perhaps 0.1% or less.
I personally think there is a moderate gap (perhaps factor of 3) between "world is ended by serious[1] spontaneous scheming" and "serious spontaneous scheming". And, I could imagine updating to a factor of 10 if the world seemed better prepared etc. So, it might be good to clarify this in the post. (Or clarify your comment.)
(I think perhaps spontaneous scheming (prior to human obsolence) is ~25% likely and x-risk conditional on being in one of those worlds which is due to this scheming is about 30% likely for an overall 8% on "world is ended by serious spontaneous scheming" (prior to human obsolence).)
serious = somewhat persistant, thoughtful, etc ↩︎
Damn, woops.
My comment was false (and strident; worst combo). I accept the strong downvote and I will try to now make a correction.
I said:
I spent a bunch of time wondering how you could could put 99.9% on no AI ever doing anything that might be well-described as scheming for any reason.
What I meant to say was:
I spent a bunch of time wondering how you could put 99.9% on no AI ever doing anything that might be well-described as scheming for any reason, even if you stipulate that it must happen spontaneously.
And now you have also commented:
Well, I have <0.1% on spontaneous scheming, period. I suspect Nora is similar and just misspoke in that comment.
So....I challenge you to list a handful of other claims that you have similar credence in. Special Relativity? P!=NP? Major changes in our understanding of morality or intelligence or mammal psychology? China pulls ahead in AI development? Scaling runs out of steam and gives way to other approaches like mind uploading? Major betrayal against you by a beloved family member?
The OP simply says "future AI systems" without specifying anything about these systems, their paradigm, or what offworld colony they may or may not be developed o...
the problem faced by evolution and by SGD is much easier than this: producing systems that behave the right way in all scenarios they are likely to encounter.
I think you mean "in all scenarios they are likely to encounter *on the training distribution* / in the ancestral environment right? That's importantly different.
In reality, the problem faced by evolution and by SGD is much easier than this: producing systems that behave the right way in all scenarios they are likely to encounter. In virtue of their aligned behavior, these systems will be “aimed at the right things” in every sense that matters in practice.
I find this passage remarkable, given that so many people are choosing to to have few or no children that fertility has fallen to 0.78 in Korea and 1.0 in China. Presumably you're aware of these (or similar) facts and intended the meaning of this passage to be compatible with them, but I'm having trouble figuring out how...
By contrast, goal realism leads only to unfalsifiable speculation about an “inner actress” with utterly alien motivations.
In order for such speculation to be unfalsifiable, it seemingly has to be the case that we're unable to ever develop good enough interpretability tools to definitively say whether the AI in question has such internal motivations. This could well turn out to be true, but I don't understand how you're able to predict this now. (Or maybe you mean something else by "unfalsifiable" but I can't see what it could be. ETA: Maybe you mean "unfalsifiable...
So you don’t need to “target the inner search,” you just need to get the system to act the way you want in all the relevant scenarios.
Your original phrase was "all scenarios they are likely to encounter", but now you've switched to "relevant scenarios". Do you not acknowledge that these two phrases are semantically very different (or likely to be interpreted very differently by many readers), since the modern world is arguably a scenario that "they are likely to encounter" (given that they actually did encounter it) but you say "the modern world is not a relevant scenario for evolution"?
Going forward, do you prefer to talk about "all scenarios they are likely to encounter", or "relevant scenarios", or both? If the latter, please clarify what you mean by "relevant"? (And please answer with respect to both evolution and AI alignment, in case the answer is different in the two cases. I'll probably have more substantive things to say once we've cleared up the linguistic issues.)
It was not at all clear to me that you intended "they are likely to encounter" to have some sort of time horizon attached to it (as opposed to some other kind of restriction, or that you meant something pretty different from the literal meaning, or that your argument/idea itself was wrong), and it's still not clear to me what sort of time horizon you have in mind.
- It seems like there are “lots of ways” that a model could end up massively overfitting and still get high training performance.
- So absent some additional story about why training won’t select an overfitter, it feels like the possibility should be getting substantive weight.
FWIW, once I learned more about the problem of induction, I realized that there do exist additional stories explaining why training won't select an overfitter. Or perhaps to put it differently, after I understood the problem of induction better it no longer seemed to me that there were lots of ways a model could massively overfit and still get high training performance. (That is, it seems to me there are many MORE ways it could not overfit)
I definitely thought you were making a counting argument over function space
I've argued multiple times that Evan was not intending to make a counting argument in function space:
- In discussion with Alex Turner (TurnTrout) when commenting on an earlier draft of this post.
- In discussion with Quintin after sharing some comments on the draft. (Also shared with you TBC.)
- In this earlier comment.
(Fair enough if you never read any of these comments.)
As I've noted in all of these comments, people consistently use terminology when making counting style arguments (except perhaps in Joe's report) which rules out the person intending the argument to be about function space. (E.g., people say things like "bits" and "complexity in terms of the world model".)
(I also think these written up arguments (Evan's talk in particular) are very hand wavy, and just provide a vague intuition. So regardless of what he was intending, the actual words of the argument aren't very solid IMO. Further, using words that rule out the intention of function space doesn't necessarily imply there is an actually good model behind these words. To actually get anywhere with this reasoning, I think you'd have to reinven...
If that's truly your remaining objection, then I think that you should retract the unmerited criticisms about how they're trying to prove 0.9999... != 1 or whatever. In my opinion, you have confidently misrepresented their arguments, and the discussion would benefit from your revisions.
This point seems right to me: if the post is specifically about representable functions than that is a valid formalization AFAICT. (Though a extremely cursed formalization for reasons mentioned in a variety of places. And if you dropped "representable", then it's extremely, extremely cursed for various analysis related reasons, though I think there is still a theoretically sound uniform measure maybe???)
It would also be nice if the original post:
- Clarified that the rebuttal is specifically about a version of the counting-argument which counts functions.
- Noted that people making counting arguments weren't intending to count functions, though this might be a common misconception about counting arguments. (Seems fine to also clarify that existing counting arguments are too hand wavy to really engage with if that's the view also.) (See also here.)
I obviously don't think the counting argument for overfitting is actually sound, that's the whole point.
Yes, I'm well aware. The problem is that when you make the counting argument for overfitting, you do so in a way that seriously misuses the formalism, which is why the argument fails. So you can't draw any lessons about counting arguments for deception from the failure of your counting argument for overfitting.
But I think the counting argument for scheming is just as obviously invalid, and misuses formalisms just as egregiously, if not moreso.
Then show me how! If you think there are errors in the math, please point them out.
Of course, it's worth stating that I certainly don't have some sort of airtight mathematical argument proving that deception is likely in neural networks—there are lots of assumptions there that could very well be wrong. But I do think that the basic style of reasoning employed by such arguments is sound.
I deny that your Kolmogorov framework is anything like "the proper formalism" for neural networks.
Err... I'm using K-complexity here because it's a simple framework to reason about, but my criticism isn't "you should use K-complexity to reason about...
I feel like there's a somewhat common argument about RL not being all that dangerous because it generalizes the training distribution cautiously - being outside the training distribution isn't going to suddenly cause an RL system to make multi-step plans that are implied but never seen in the training distribution, it'll probably just fall back on familiar, safe behavior.
To me, these arguments feel like they treat present-day model-free RL as the "central case," and model-based RL as a small correction.
Anyhow, good post, I like most of the arguments, I just felt my reaction to this particular one could be made in meme format.
There are compute tradeoffs and you're doing to run only as many MCTS rollouts as you need to get good performance.
I completely agree. Smart agents will run only as many MCTS rollouts as they need to get good performance, no more - and no less. (And the smarter they are, and so the more compute they have access to, the more MCTS rollouts they are able to run, and the more they can change the default reactive policy.)
But 'good performance' on what, exactly? Maximizing utility. That's what a model-based RL agent (not a simple-minded, unintelligent, myopic model-free policy like a frog's retina) does.
If the Value of Information remains high from doing more MCTS rollouts, then an intelligent agent will keep doing rollouts for as long as the additional planning continues to pay its way in expected improvements. The point of doing planning is policy/value improvement. The more planning you do, the more you can change the original policy. (This is how you train AlphaZero so far from its prior policy, of a randomly-initialized CNN playing random moves, to its final planning-improved policy, a superhuman Go player.) Which may take it arbitrarily far in terms of policy - like, for example...
Speaking of GPT-4 o1-mini/preview, I think I might've accidentally already run into an example of search's characteristic 'flipping' or 'switching', where at a certain search depth, it abruptly changes to a completely different, novel, unexpected (and here, undesired) behavior.
So one of my standard tests is the 'S' poem from the Cyberiad: "Have it compose a poem---a poem about a haircut! But lofty, noble, tragic, timeless, full of love, treachery, retribution, quiet heroism in the face of certain doom! Six lines, cleverly rhymed, and every word beginning with the letter 's'!"
This is a test most LLMs do very badly on, for obvious reasons; tokenization aside, it is pretty much impossible to write a decent poem which satisfies these constraints purely via a single forward pass with no planning, iteration, revision, or search. Neither you, I, nor the original translator could do that; GPT-3 couldn't do it, GPT-4o still can't do it; and I've never seen a LLM do it. (They can revise it if you ask, but the simple approach tends to hit local optima where there are still a lot of words violating the 's'-constraint.) But the original translation's poem is also obscure enough that they don'...
This monograph by Bertsekas on the interrelationship between offline RL and online MCTS/search might be interesting -- http://www.athenasc.com/Frontmatter_LESSONS.pdf -- since it argues that we can conceptualise the contribution of MCTS as essentially that of a single Newton step from the offline start point towards the solution of the Bellman equation. If this is actually the case (I haven't worked through all details yet) then this seems to be able to be used to provide some kind of bound on the improvement / divergence you can get once you add online planning to a model-free policy.
Nora and/or Quentin: you talk a lot about inductive biases of neural nets ruling scheming out, but I have a vague sense that scheming ought to happen in some circumstances - perhaps rather contrived, but not so contrived as to be deliberately inducing the ulterior motive. Do you expect this to be impossible? Can you propose a set of conditions you think sufficient to rule out scheming?
More generally, John Miller and colleagues have found training performance is an excellent predictor of test performance, even when the test set looks fairly different from the training set, across a wide variety of tasks and architectures.
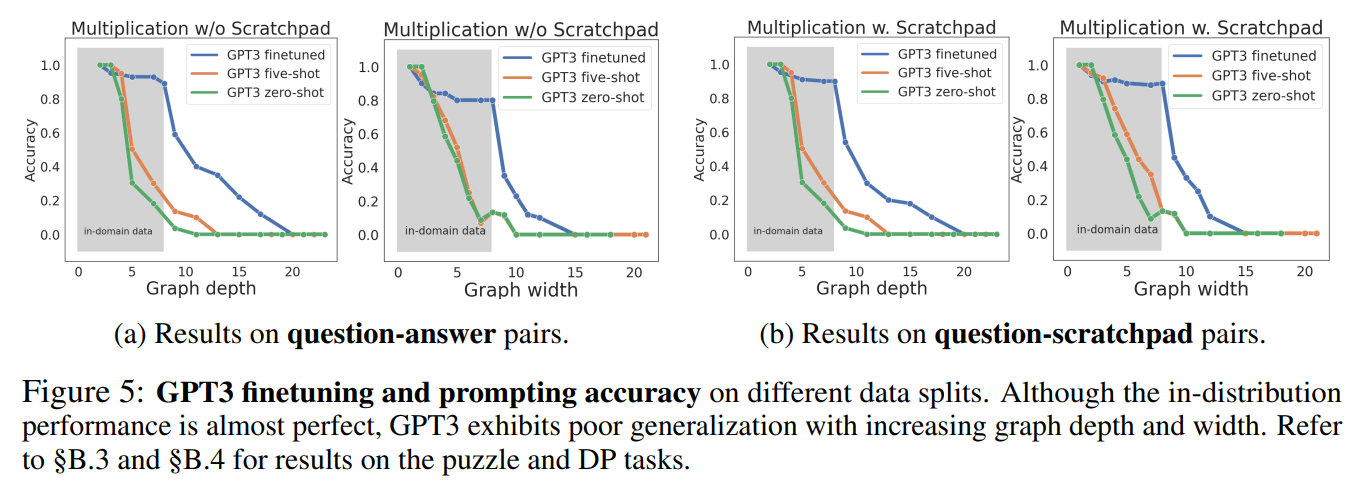
Counterdatapoint to [training performance being an excellent predictor of test performance]: in this paper, GPT-3 was fine-tuned to multiply "small" (e.g., 3-digit by 3-digit) numbers, which didn't generalize to multiplying bigger numbers.
Overfitting networks are free to implement a very simple function— like the identity function or a constant function— outside the training set, whereas generalizing networks have to exhibit complex behaviors on unseen inputs. Therefore overfitting is simpler than generalizing, and it will be preferred by SGD.
You're conflating the simplicity of a function in terms of how many parameters are required to specify it, in the abstract, and simplicity in terms of how many neural network parameters are fixed.
The actual question should be something like "how ...
In favour of goal realism
Suppose your looking at an AI that is currently placed in a game of chess.
It has a variety of behaviours. It moves pawns forward in some circumstances. It takes a knight with a bishop in a different circumstance.
You could describe the actions of this AI by producing a giant table of "behaviours". Bishop taking behaviours in this circumstance. Castling behaviour in that circumstance. ...
But there is a more compact way to represent similar predictions. You can say it's trying to win at chess.
The "trying to win...
I wrote up my views on the principle of indifference here:
https://www.lesswrong.com/posts/3PXBK2an9dcRoNoid/on-having-no-clue
I agree that it has certain philosophical issues, but I don’t believe that this is as fatal to counting arguments as you believe.
Towards the end I write:
“The problem is that we are making an assumption, but rather than owning it, we're trying to deny that we're making any assumption at all, ie. "I'm not assuming a priori A and B have equal probability based on my subjective judgement, I'm using the principle of indifference". Roll to...
Despite not answering all possible goal-related questions a priori, the reductionist perspective does provide a tractable research program for improving our understanding of AI goal development. It does this by reducing questions about goals to questions about behaviors observable in the training data.
[emphasis mine]
This might be described as "a reductionist perspective". It is certainly not "the reductionist perspective", since reductionist perspectives need not limit themselves to "behaviors observable in the training data".
A more reasonable-to-my-mind b...
This post and (imo more importantly) the discussion it spurred has been pretty helpful for how I think about scheming. I'm happy that it was written!
We can salvage a counting argument. But it needs to be a little subtle. And it's all about the comments, not the code.
Suppose a neural network has 1 megabyte of memory. To slightly oversimplify, lets say it can represent a python file of 1 megabyte.
One option is for the network to store a giant lookup table. Lets say the network needs half a megabyte to store the training data in this table. This leaves the other half free to be any rubbish. Hence around possible networks.
The other option is for the network to implement a simple ...
The reason SDG doesn't overfit large neural networks is probably because of various measures specifically intended to prevent overfitting, like weight penalties, dropout, early stopping, data augmentation + noise on inputs, and large enough learning rates that prevent convergence. If you didn't do those, running SDG to parameter convergence would probably cause overfitting. Furthermore, we test networks on validation datasets on which they weren't trained, and throw out the networks that don't generalize well to the validation set and start over (with new ...
More generally, John Miller and colleagues have found training performance is an excellent predictor of test performance, even when the test set looks fairly different from the training set, across a wide variety of tasks and architectures.
Seems like figure 1 from Miller et al is a plot of test performance vs. "out of distribution" test performance. One might expect plots of training performance vs. "out of distribution" test performance to have more spread.
To goal realism vs goal reductionism, I would say: why not both?
I think that really highly capable AGI is likely to have both heuristics and behaviors that come from training and also internal thought processes, maybe done by LLM or LLM-like module or directly from the more complex network. This process would incorporate having some preferences and hence goals (even if temporary, changed between tasks).
I wouldn't say that the presented "counting argument" is a "central reason". The central reason is an a priori notion that if "x can be achieved by scheming" someone who wants x will scheme
A point about counting arguments that I have not seen made elsewhere (although I may have missed it!).
The failure of the counting argument that SGD should result in overfitting is not a valid countexample! There is a selection bias here - the only reason we are talking about SGD is *because* it is a good learning algorithm that does not overfit. It could well still be true that almost all counting arguments are true about almost all learning algorithms. The fact that SGD does generalises well is an exception *by design*.
The principle fails even in these simple cases if we carve up the space of outcomes in a more fine-grained way. As a coin or a die falls through the air, it rotates along all three of its axes, landing in a random 3D orientation. The indifference principle suggests that the resting states of coins and dice should be uniformly distributed between zero and 360 degrees for each of the three axes of rotation. But this prediction is clearly false: dice almost never land standing up on one of their corners, for example.
The only way I can parse this is that...
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2025. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
The indifference principle is making the mistake of using a uniform prior, when a true bayesian uses the Jeffreys prior
...We can also construct an analogous simplicity argument for overfitting:
Overfitting networks are free to implement a very simple function— like the identity function or a constant function— outside the training set, whereas generalizing networks have to exhibit complex behaviors on unseen inputs. Therefore overfitting is simpler than generalizing, and it will be preferred by SGD.
Prima facie, this parody argument is about as plausible as the simplicity argument for scheming. Since its conclusion is false, we should reject the argumentative form on which it i
I buy the argument that scheming won't happen conditionally on the fact that we don't allow much slack between different optimisation steps. As Quentin mentions in his AXRP podcast episode, SGD doesn't have close to the same level of slack that, for example, cultural evolution allowed. (See the entire free energy of optimisation debate here from before, can't remember the post names ;/) Iff that holds, then I don't see why the inner behaviour should diverge from what the outer alignment loop specifies.
I do, however, believe that ensuring that this is true ...
I think this is an excellent post. I really liked the insight about the mechanisms (and mistakes) shared by the counting arguments behind AI doom and behind "deep learning surely won't generalize." Thank you for writing this; these kinds of loose claims have roamed freely for far too long.
EDIT: Actually this post is weaker than a draft I'd read. I still think it's good, but missing some of the key points I liked the most. And I'm not on board with all of the philosophical claims about e.g. generalized objections to the principle of indifference (in part because I don't understand them).
Crossposted from the AI Optimists blog.
AI doom scenarios often suppose that future AIs will engage in scheming— planning to escape, gain power, and pursue ulterior motives, while deceiving us into thinking they are aligned with our interests. The worry is that if a schemer escapes, it may seek world domination to ensure humans do not interfere with its plans, whatever they may be.
In this essay, we debunk the counting argument— a central reason to think AIs might become schemers, according to a recent report by AI safety researcher Joe Carlsmith.[1] It’s premised on the idea that schemers can have “a wide variety of goals,” while the motivations of a non-schemer must be benign by definition. Since there are “more” possible schemers than non-schemers, the argument goes, we should expect training to produce schemers most of the time. In Carlsmith’s words:
We begin our critique by presenting a structurally identical counting argument for the obviously false conclusion that neural networks should always memorize their training data, while failing to generalize to unseen data. Since the premises of this parody argument are actually stronger than those of the original counting argument, this shows that counting arguments are generally unsound in this domain.
We then diagnose the problem with both counting arguments: they rest on an incorrect application of the principle of indifference, which says that we should assign equal probability to each possible outcome of a random process. The indifference principle is controversial, and is known to yield absurd and paradoxical results in many cases. We argue that the principle is invalid in general, and show that the most plausible way of resolving its paradoxes also rules out its application to an AI’s behaviors and goals.
More generally, we find that almost all arguments for taking scheming seriously depend on unsound indifference reasoning. Once we reject the indifference principle, there is very little reason left to worry that future AIs will become schemers.
The counting argument for overfitting
Counting arguments often yield absurd conclusions. For example:
This isn’t a merely hypothetical argument. Prior to the rise of deep learning, it was commonly assumed that models with more parameters than data points would be doomed to overfit their training data. The popular 2006 textbook Pattern Recognition and Machine Learning uses a simple example from polynomial regression: there are infinitely many polynomials of order equal to or greater than the number of data points which interpolate the training data perfectly, and “almost all” such polynomials are terrible at extrapolating to unseen points.
Let’s see what the overfitting argument predicts in a simple real-world example from Caballero et al. (2022), where a neural network is trained to solve 4-digit addition problems. There are 10,0002 = 100,000,000 possible pairs of input numbers, and 19,999 possible sums, for a total of 19,999100,000,000 ≈ 1.10 ⨉ 10430,100,828 possible input-output mappings.[2] They used a training dataset of 992 problems, so there are therefore 19,999100,000,000 – 992 ≈ 2.75 ⨉ 10430,096,561 functions that achieve perfect training accuracy, and the proportion with greater than 50% test accuracy is literally too small to compute using standard high-precision math tools.[3] Hence, this argument predicts virtually all networks trained on this problem should massively overfit— contradicting the empirical result that networks do generalize to the test set.
The argument also predicts that larger networks— which can express a wider range of functions, most of which perform poorly on the test set— should generalize worse than smaller networks. But empirically, we find the exact opposite result: wider networks usually generalize better, and never generalize worse, than narrow networks.[4] These results strongly suggest that SGD is not doing anything like sampling uniformly at random from the set of representable functions that do well on the training set.
More generally, John Miller and colleagues have found training performance is an excellent predictor of test performance, even when the test set looks fairly different from the training set, across a wide variety of tasks and architectures.
These results clearly show that the conclusion of our parody argument is false. Neural networks almost always learn genuine patterns in the training set which do generalize, albeit imperfectly, to unseen test data.
Dancing through a minefield of bad networks
One possible explanation for these results is that deep networks simply can’t represent functions that fail to generalize, so we shouldn’t include misgeneralizing networks in the space of possible outcomes. But it turns out this hypothesis is empirically false.
Tom Goldstein and colleagues have found it’s possible to find misgeneralizing neural nets by adding a term to the loss function which explicitly rewards the network for doing poorly on a validation set. The resulting “poisoned” models achieve near perfect accuracy on the training set while doing no better than random chance on a held out test set.[5] What’s more, the poisoned nets are usually quite “close” in parameter space to the generalizing networks that SGD actually finds— see the figure below for a visualization.
Dancing through a minefield of bad minima: we train a neural net classifier and plot the iterates of SGD after each tenth epoch (red dots). We also plot locations of nearby “bad” minima with poor generalization (blue dots). We visualize these using t-SNE embedding. All blue dots achieve near perfect train accuracy, but with test accuracy below 53% (random chance is 50%). The final iterate of SGD (yellow star) also achieves perfect train accuracy, but with 98.5% test accuracy. Miraculously, SGD always finds its way through a landscape full of bad minima, and lands at a minimizer with excellent generalization.
Against the indifference principle
What goes wrong in the counting argument for overfitting, then? Recall that both counting arguments involve an inference from “there are ‘more’ networks with property X” to “networks are likely to have property X.” This is an application of the principle of indifference, which says that one should assign equal probability to every possible outcome of a random process, in the absence of a reason to think certain outcomes are favored over others.[6]
The indifference principle gets its intuitive plausibility from simple cases like fair coins and dice, where it seems to give the right answers. But the only reason coin-flipping and die-rolling obey the principle of indifference is that they are designed by humans to behave that way. Dice are specifically built to land on each side ⅙ of the time, and if off-the-shelf coins were unfair, we’d choose some other household object to make random decisions. Coin flips and die rolls, then, can’t be evidence for the validity of the indifference principle as a general rule of probabilistic reasoning.
The principle fails even in these simple cases if we carve up the space of outcomes in a more fine-grained way. As a coin or a die falls through the air, it rotates along all three of its axes, landing in a random 3D orientation. The indifference principle suggests that the resting states of coins and dice should be uniformly distributed between zero and 360 degrees for each of the three axes of rotation. But this prediction is clearly false: dice almost never land standing up on one of their corners, for example.
Even worse, by coarse-graining the possibilities, we can make the indifference principle predict that any event has a 50% chance of occuring (“either it happens or it doesn’t”). In general, indifference reasoning produces wildly contradictory results depending on how we choose to cut up the space of outcomes.[7] This problem is serious enough to convince most philosophers that the principle of indifference is simply false.[8] On this view, neither counting argument can get off the ground, because we cannot infer that SGD is likely to select the kinds of networks that are more numerous.
Against goal realism
Even if you’re inclined to accept some form of indifference principle, it’s clear that its applicability must be restricted in order to avoid paradoxes. For example, philosopher Michael Huemer suggests that indifference reasoning should only be applied to explanatorily fundamental variables. That is, if X is a random variable which causes or “explains” another variable Y, we might be able to apply the indifference principle to X, but we definitely can’t apply it to Y.[9]
While we don’t accept Huemer’s view, it seems like many people worried about scheming do implicitly accept something like it. As Joe Carlsmith explains:
Here, the goal slot is clearly meant to be causally and explanatorily prior to the goal-achieving engine, and hence to the rest of the AI’s behavior. On Huemer’s view, this causal structure would validate the application of indifference reasoning to goals, but not to behaviors, thereby breaking the symmetry between the counting arguments for overfitting and for scheming. We visually depict this view of AI cognition on the lefthand side of the figure below.
We’ll call the view that goals are explanatorily fundamental, “goal realism.” On the opposing view, which we’ll call goal reductionism, goal-talk is just a way of categorizing certain patterns of behavior. There is no true underlying goal that an AI has— rather, the AI simply learns a bunch of contextually-activated heuristics, and humans may or may not decide to interpret the AI as having a goal that compactly explains its behavior. If the AI becomes self-aware, it might even attribute goals to itself— but either way, the behaviors come first, and goal-attribution happens later.
Notably, some form of goal reductionism seems to be quite popular among naturalistic philosophers of mind, including Dan Dennett,[10] Paul and Patricia Churchland, and Alex Rosenberg.[11] Readers who are already inclined to accept reductionism as a general philosophical thesis— as Eliezer Yudkowsky does— should probably accept reductionism about goals.[12] And even if you’re not a global reductionist, there are pretty strong reasons for thinking behaviors are more fundamental than goals, as we’ll see below.
Goal slots are expensive
Should we actually expect SGD to produce AIs with a separate goal slot and goal-achieving engine?
Not really, no. As a matter of empirical fact, it is generally better to train a whole network end-to-end for a particular task than to compose it out of separately trained, reusable modules. As Beren Millidge writes,
We have good reason, then, to think that future AIs will not have the kind of architecture that makes goal realism superficially plausible. And as we will see below, goal realism fails even for AIs with explicit internal “goals” and search procedures.
Inner goals would be irrelevant
The idea of AI scheming was introduced in its modern form in the paper Risks from Learned Optimization. It describes systems with inner goals as “internally searching through a search space [..] looking for those elements that score high according to some objective function that is explicitly represented within the system”. But even if we accept that future ML systems will develop such an internal process, it’s not clear that this inner objective function would have much relation to the goals which best describe the system’s actual behavior.
For example, imagine a hospital’s medical operation planning system that internally looks like “query an LLM for N possible operation plans, feed each plan to a classifier trained to estimate the odds of a given plan leading to a medical malpractice lawsuit, and pick the plan that scores lowest.”[13] The overall behavioral goal of this system need not be well described as “minimize the odds of a malpractice lawsuit.” Instead, whatever behavioral goals we should ascribe to the system will depend on the interaction between the LLM’s prior over operation plans and the classifier’s scoring of those plans. The “inner objective” acts less like the “true goal of the system,” and more like a Bayesian update on the LLM’s prior over operation plans.
Even as we increase the power of the inner optimizer by setting N to arbitrarily large values, it seems unlikely that the resulting system would generate plans that actively sought to minimize the probability of a malpractice lawsuit in flexible, creative or dangerous ways. Rather, the system would produce adversarial examples to the classifier, such as instructing staff to constantly clean a surgical room, and not actually perform a surgery.
In particular, increasing N would not lead to the system producing “scheming” plans to advance the inner objective. A classifier trained to distinguish between historical medical plans that led to malpractice lawsuits versus those that didn’t, is not going to assign extreme scores to plans like “hack into the server hosting me in order to set the classifier scores to extreme values” or “blackmail the hospital administration into canceling all future surgeries”, because such plans do not optimally express the simple features that distinguish safe versus risky plans in the training data (e.g., mentions of blackmail / hacking could be replaced with mentions of checking procedure / cleaning / etc).
The point: even arbitrary amounts of internal optimization power directed towards a simple inner objective can fail to lead to any sort of “globally coherent” pursuit of that objective in the system’s actual behaviors. The goal realist perspective relies on a trick of language. By pointing to a thing inside an AI system and calling it an “objective”, it invites the reader to project a generalized notion of “wanting” onto the system’s imagined internal ponderings, thereby making notions such as scheming seem more plausible.
However, the actual mathematical structure being posited doesn’t particularly support such outcomes. Why assume emergent “inner objectives” will support creative scheming when “optimized for”? Why assume that internal classifiers that arose to help encourage correct outputs during training would have extrema corresponding to complex plans that competently execute extremely out-of-distribution actions in the real world? The extrema of deliberately trained neural classifiers do not look anything like that. Why should emergent internal neural classifiers be so different?
Goal realism is anti-Darwinian
Goal realism can lead to absurd conclusions. It led the late philosopher Jerry Fodor to attack the theory of natural selection on the grounds that it can’t resolve the underdetermination of mental content. Fodor pointed out that nature has no way of selecting, for example, frogs that “aim at eating flies in particular” rather than frogs that target “little black dots in the sky,” or “things that smell kind of like flies,” or any of an infinite number of deviant, “misaligned” proxy goals which would misgeneralize in counterfactual scenarios. No matter how diverse the ancestral environment for frogs might be, one can always come up with deviant mental contents which would produce behavior just as adaptive as the “intended” content:
As Rosenberg (2013) points out, Fodor goes wrong by assuming there exists a real, objective, perfectly determinate “inner goal” whose content must be pinned down by the selection process.[14] But the physical world has no room for goals with precise contents. Real-world representations are always fuzzy, because they are human abstractions derived from regularities in behavior.
Like contemporary AI pessimists, Fodor’s goal realism led him to believe that selection processes face an impossibly difficult alignment problem— producing minds whose representations are truly aimed at the “correct things,” rather than mere proxies. In reality, the problem faced by evolution and by SGD is much easier than this: producing systems that behave the right way in all scenarios they are likely to encounter. In virtue of their aligned behavior, these systems will be “aimed at the right things” in every sense that matters in practice.
Goal reductionism is powerful
Under the goal reductionist perspective, it’s easy to predict an AI’s goals. Virtually all AIs, including those trained via reinforcement learning, are shaped by gradient descent to mimic some training data distribution.[15] Some data distributions illustrate behaviors that we describe as “pursuing a goal.” If an AI models such a distribution well, then trajectories sampled from its policy can also be usefully described as pursuing a similar goal to the one illustrated by the training data.
The goal reductionist perspective does not answer every possible goal-related question we might have about a system. AI training data may illustrate a wide range of potentially contradictory goal-related behavioral patterns. There are major open questions, such as which of those patterns become more or less influential in different types of out-of-distribution situations, how different types of patterns influence the long-term behaviors of “agent-GPT” setups, and so on.
Despite not answering all possible goal-related questions a priori, the reductionist perspective does provide a tractable research program for improving our understanding of AI goal development. It does this by reducing questions about goals to questions about behaviors observable in the training data. By contrast, goal realism leads only to unfalsifiable speculation about an “inner actress” with utterly alien motivations.
Other arguments for scheming
In comments on an early draft of this post, Joe Carlsmith emphasized that the argument he finds most compelling is what he calls the “hazy counting argument,” as opposed to the “strict” counting argument we introduced earlier. But we think our criticisms apply equally well to the hazy argument, which goes as follows:
Joe admits this argument is “not especially principled.” We agree: it relies on applying the indifference principle— itself a dubious assumption— to an ill-defined set of “ways” a model could develop throughout training. There is also a hazy counting argument for overfitting:
While many machine learning researchers have felt the intuitive pull of this hazy overfitting argument over the years, we now have a mountain of empirical evidence that its conclusion is false. Deep learning is strongly biased toward networks that generalize the way humans want— otherwise, it wouldn’t be economically useful.
Simplicity arguments
Joe also discusses simplicity arguments for scheming, which suppose that schemers may be “simpler” than non-schemers, and therefore more likely to be produced by SGD. Specifically, since schemers are free to have almost any goal that will motivate them to act aligned during training, SGD can give them very simple goals, whereas a non-schemer has to have more specific, and therefore more complex, goals.
There are several problems with this argument. The first is that “simplicity” is a highly ambiguous term, and it’s not clear which, if any, specific notion of simplicity should be relevant here. One reasonable definition of “simple” is “low description length,” which directly implies “more likely” if we assume the language in which the hypotheses are being described is efficient (assigns short encodings to likely hypotheses). But on this view, simplicity is simply another word for likelihood: we can’t appeal to our intuitive notions of simplicity to conclude that one hypothesis will truly be “simpler” and hence more likely.
Alternatively, one could appeal to the actual inductive biases of neural network training, as observed empirically or derived theoretically. We will address this question in greater detail in a future post. However, we believe that current evidence about inductive biases points against scheming for a variety of reasons. Very briefly:
We can also construct an analogous simplicity argument for overfitting:
Prima facie, this parody argument is about as plausible as the simplicity argument for scheming. Since its conclusion is false, we should reject the argumentative form on which it is based.
Conclusion
In this essay, we surveyed the main arguments that have been put forward for thinking that future AIs will scheme against humans by default. We find all of them seriously lacking. We therefore conclude that we should assign very low credence to the spontaneous emergence of scheming in future AI systems— perhaps 0.1% or less.
On page 21 of his report, Carlsmith writes: ‘I think some version of the “counting argument” undergirds most of the other arguments for expecting scheming that I’m aware of (or at least, the arguments I find most compelling). That is: schemers are generally being privileged as a hypothesis because a very wide variety of goals could in principle lead to scheming…’
Each mapping would require roughly 179 megabytes of information to specify.
It underflows to zero in the Python mpmath library, and WolframAlpha times out.
This is true when using the maximal update parametrization (µP), which scales the initialization variance and learning rate hyperparameters to match a given width.
That is, the network’s misgeneralization itself generalizes from the validation set to the test set.
Without an indifference principle, we might think that SGD is strongly biased toward producing non-schemers, even if there are “more” schemers.
Other examples include Bertrand’s paradox and van Fraassen’s cube factory paradox.
“Probably the dominant response to the paradoxes of the Principle of Indifference is to declare the Principle false. It is said that the above examples show the Principle to be inconsistent.” — Michael Huemer, Paradox Lost, pg. 168
“Given two variables, X and Y, if X explains Y, then the initial probability distribution for Y must be derived from that for X (or something even more fundamental). Here, by ‘initial probabilities’, I mean probabilities prior to relevant evidence. Thus, if we are applying the Principle of Indifference, we should apply it at the more fundamental level.” — Michael Huemer, Paradox Lost, pg. 175
See the Wikipedia article on the intentional stance for more discussion of Dennett’s views.
Rosenberg and the Churchlands are anti-realists about intentionality— they deny that our mental states can truly be “about” anything in the world— which implies anti-realism about goals.
This is not an airtight argument, since a global reductionist may want to directly reduce goals to brain states, without a “detour” through behaviors. But goals supervene on behavior— that is, an agent’s goal can’t change without a corresponding change in its behavior in some possible scenario. (If you feel inclined to deny this claim, note that a change in goals without a change in behavior in any scenario would have zero practical consequences.) If X supervenes on Y, that’s generally taken to be an indication that Y is “lower-level” than X. By contrast, it’s not totally clear that goals supervene on neural states alone, since a change in goals may be caused by a change in external circumstances rather than any change in brain state. For further discussion, see the SEP article on Externalism About the Mind and Alex Flint’s LessWrong post, “Where are intentions to be found?”
Readers might object to this simple formulation for an inner optimizer and argue that any “emergent” inner objectives would be implemented differently, perhaps in a more “agenty” manner. Real inner optimizers are very unlikely to follow the simplified example provided here. Their optimization process is very unlikely to look like a single step of random search with sample size N.
However, real inner optimizers would still be similar in their core dynamics. Anything that looks like ““internally searching through a search space [..] looking for those elements that score high according to some objective function that is explicitly represented within the system” is ultimately some method of using scores from an internal classifier to select for internal computations that have higher scores.
The system’s method of aligning internal representations with classifier scores may introduce some “inductive biases” that also influence the model’s internals. Any such “inductive bias” would only further undermine the goal realist perspective by further separating the actual behavioral goals the overall system pursues from internal classifier’s scores.
In this lecture, Fodor repeatedly insists that out of two perfectly correlated traits like “snaps at flies” (T1) and “snaps at ambient black dots” (T2) where only one of them “causes fitness,” there has to be a fact of the matter about which one is “phenotypic.”
The correspondence between RL and probabilistic inference has been known for years. RL with KL penalties is better viewed as Bayesian inference, where the reward is “evidence” about what actions to take and the KL penalty keeps the model from straying too far from the prior. RL with an entropy bonus is also Bayesian inference, where the prior is uniform over all possible actions. Even when there is no regularizer, we can view RL algorithms like REINFORCE as a form of “generalized” imitation learning, where trajectories with less-than-expected reward are negatively imitated.
Assuming hypercomputation is impossible in our universe.