Book Review: Design Principles of Biological Circuits
36Ben Pace
9Richard_Ngo
29Ofer
30johnswentworth
4Davidmanheim
27Rohin Shah
11johnswentworth
5redlizard
13johnswentworth
3Rohin Shah
24[anonymous]
17Michael McLaren
13habryka
10Ben Pace
8NancyLebovitz
7[anonymous]
4johnswentworth
3[anonymous]
6drewendy
6DanielFilan
5Kenny
5mako yass
3Thomas Kwa
2johnswentworth
New Comment
Curated. Just discussed this with Oli a bunch. Some reasons for curation:
- High quality book reviews are very valuable and a key step in being able to interface with expertise in other communities and fields.
- Biology is a field that is a major blindspot on LessWrong, where most of us have relatively little expertise. One reason for this is that we take a very reductionistic approach to understanding the world, and biology often seems very messy and unprincipled. This post really shocked me with the level of principle that apparently can be found in such systems. Not only were things that seemed like wasted energy actually useful, and not only were they useful in ways common to a wide variety of biological systems, but their use is to enforce abstractions so that the whole system becomes more reliable and easier for us to model. This is quite something. I hope others here on LW who look into biology are able to build on this.
Excellent post, looking forward to further on this topic.
This post really shocked me with the level of principle that apparently can be found in such systems.
If you're interested in this theme, I recommend reading up on convergent evolution, which I find really fascinating. Here's Dawkins in The Blind Watchmaker:
The primitive mammals that happened to be around in the three areas [of Australia, South America and the Old World] when the dinosaurs more or less simultaneously vacated the great life trades, were all rather small and insignificant, probably nocturnal, previously overshadowed and overpowered by the dinosaurs. They could have evolved in radically different directions in the three areas. To some extent this is what happened. … But although the separate continents each produced their unique mammals, the general pattern of evolution in all three areas was the same. In all three areas the mammals that happened to be around at the start fanned out in evolution, and produced a specialist for each trade which, in many cases, came to bear a remarkable resemblance to the corresponding specialist in the other two areas.
Dawkins goes on to describe the many ways in which marsupials in Australia, placentals in the Old World, and a mix of both in South America underwent convergent evolution to fill similar roles in their ecosystems. Some examples are very striking: separate evolutions of moles, anteaters, army ants, etc.
I'm also working my way through Jonathan Losos' Improbable Destinies now, which isn't bad but a bit pop-sciencey. For more detail, Losos mentions https://mitpress.mit.edu/books/convergent-evolution and https://www.amazon.co.uk/Lifes-Solution-Inevitable-Humans-Universe/dp/0521603250.
Thanks for writing this!
I used to agree with this position. I used to argue that there was no reason to expect human-intelligible structure inside biological organisms, or deep neural networks, or other systems not designed to be understandable. But over the next few years after that biologist’s talk, I changed my mind, and one major reason for the change is Uri Alon’s book An Introduction to Systems Biology: Design Principles of Biological Circuits.
I'm curious what you think about the following argument:
The examples in this book are probably subject to a strong selection effect: examples for mechanisms that researchers currently understand were more likely to be included in the book than those that no one has a clue about. There might be a large variance in the "opaqueness" of biological mechanisms (in different levels of abstraction). So perhaps this book provides little evidence on the (lack of) opaqueness of, say, the mechanisms that allowed John von Neumann to create the field of cellular automata, at a level of abstraction that is analogous to artificial neural networks.
Yeah, that's a natural argument. The counterargument which immediately springs to mind is that, until we've completely and totally solved biology, there's always going to be some systems we don't understand yet - just because they haven't been understood yet does not mean they're opaque. It boils down to priors: do we have reasons to expect large variance in opaqueness? Do we have reason to expect low variance in opaqueness?
My own thoughts can be summarized by three main lines of argument:
- If we look at the entire space of possible programs, it's not hard to find things which are pretty darn opaque to humans. Crypto and computational complexity theory provide some degree of foundation to that idea. So human-opaque systems do exist.
- We can know that something is non-opaque (by understanding it), but we can't know for sure that something is opaque. Lack of understanding is Bayesian evidence in favor of opaqueness, but the strength of that evidence depends a lot on who's tried to understand it, how much effort was put in, what the incentives look like, etc.
- I personally have made arguments of the form "X is intractably opaque to humans" about many different systems in multiple different fields in the past (not just biology). In most cases, I later turned out to be wrong. So at this point I have a pretty significant prior against opacity.
So I'd say the book provides evidence in favor of a generally-low prior on opaqueness, but people trying and failing to understand a system is the main type of evidence regarding opacity of particular systems.
Unfortunately, these are all outside-view arguments. I do think an inside view is possible here - it intuitively feels like the kinds of systems which turned out not to be opaque (e.g. biological circuits) have visible, qualitative differences from the kinds of systems which we have some theoretical reasons to consider opaque (e.g. pseudorandom number generators). They're the sort of systems people call "emergent". Problem is, we don't have a useful formalization of that idea, and I expect that figuring it out requires solving a large chunk of the problems in the embedded agency cluster.
When I get around to writing a separate post on Alon's last chapter (evolution of modularity), that will include some additional relevant insight to the question.
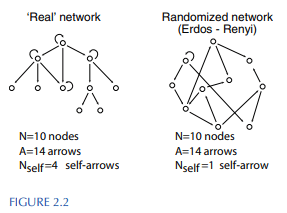
It's not just selection effects on organisms - it's within organisms. The examples given are NOT fully understood, so (for example,) the bacterial transcription network motifs only contain the relationships that we understand. Given that loops and complex connections are harder to detect, that has selected for simplicity.
Given that, I still want to read the book and see the argument more fully.
It seems like there are two claims here:
- Biological systems are not random, in the sense that they have purpose
- Biological systems are human-understandable with enough effort
The first one seems to be expected even under the "everything is a mess" model -- even though evolution is just randomly trying things, the only things that stick around are the ones that are useful, so you'd expect that most things that appear on first glance to be useless actually do have some purpose.
The second one is the claim I'm most interested in.
Some of your summaries seem to be more about the first claim. For Chapters 7-8:
For our purposes, the main takeaway from these two chapters is that, just because the system looks wasteful/arbitrary, does not mean it is. Once we know what to look for, it becomes clear that the structure of biological systems is not nearly so arbitrary as it looks.
This seems to be entirely the first claim.
The other chapters seem like they do mostly address the second claim, but it's a bit hard to tell. I'm curious if, now knowing about these two distinct claims, you still think the book is strong evidence for the second claim? What about chapters 7-8 in particular?
I intended the claim to be entirely the second. The first is relevant mainly as a precondition for the second, and as a possible path to human understanding.
Chapters 7-8 are very much aimed at human understanding of the systems used for robust recognition and signal-passing, and I consider both those chapters and the book to be strong evidence that human understanding is tractable.
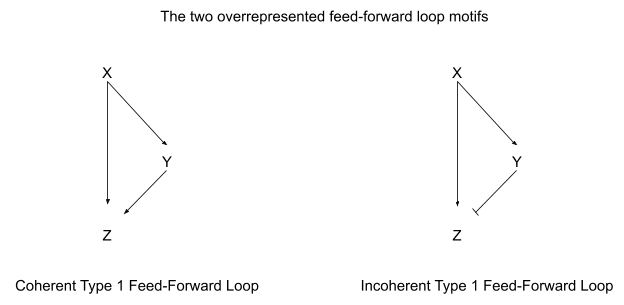
Regarding the "not random" claim, I'm guessing you're looking at many of the statistical claims? E.g. things like "only a handful of specific designs work". Those are obviously evidence of biological systems not being random, but more importantly, they're evidence that humans can see and understand ways in which biological systems are not random. Not only is there structure, that structure is human-understandable - i.e. repeated biochemical circuit designs.
This second claim sounds to me as being a bit trivial. Perhaps it is my reverse engineering background, but I have always taken it for granted that approximately any mechanism is understandable by a clever human given enough effort.
This book [and your review] explains a number of particular pieces of understanding of biological systems in detail, which is super interesting; but the mere point that these things can be understood with sufficient study almost feels axiomatic. Ignorance is in the map, not the territory; there are no confusing phenomena, only minds confused by phenomena; etc. Even when I knew nothing about this biological machinery, I never imagined for a second that no understanding was attainable in principle. I only saw *systems that are not optimized for ease of understanding*, and therefore presumably more challenging to understand than systems designed by human engineers which *are* optimized for ease of understanding.
But I get the impression that the real point you are shooting for (and possibly, the point the book is shooting for) is a stronger point than this. Not so much "there is understanding to be had here, if you look deeply enough", but rather a claim about what *particular type of structure* we are likely to find, and how this may or may not conform to the type of structure that humans are trained to look for.
Is this true? If it is, could you expand on this distinction?
The second claim was actually my main goal with this post. It is a claim I have heard honest arguments against, and even argued against myself, back in the day. A simple but not-particularly-useful version of the argument would be something like "the shortest program which describes biological behavior may be very long", i.e. high Kolmogorov complexity. If that program were too long to fit in a human brain, then it would be impossible for humans to "understand" the system, in some sense. We could fit the program in a long book, maybe, but since the program itself would be incompressible it would just look like thousands of pages of random noise - indeed, it would be random noise, in a very rigorous sense.
That said, while I don't think either Alon or I were making claims about what particular structure we're likely to find here, I do think there is a particular kind of structure here. I do not currently know what that structure is, but I think answering that question (or any of several equivalent questions, e.g. formalizing abstraction) is the main problem required to solve embedded agency and AGI in general.
Also see my response to Ofer, which discusses the same issues from a different starting point.
Excited to see that the author of this book, Uri Alon, just tweeted about this review.
A beautiful and insightful review of Introduction to Systems Biology, 2nd edition, emphasizing the routes to simplicity in biological systems:
https://lesswrong.com/posts/bNXdnRTpSXk9p4zmi/book-review-design-principles-of-biological-circuits.
For those who are interested, the class that Uri Alon teaches that goes with this textbook is on YouTube
This post surprised me a lot. It still surprises me a lot, actually. I've also linked it a lot of times in the past year.
The concrete context where this post has come up is in things like ML transparency research, as well as lots of theories about what promising approaches to AGI capabilities research are. In particular, there is a frequently recurring question of the type "to what degree do optimization processes like evolution and stochastic gradient descent give rise to understandable modular algorithms?".
This post was a qualitative step forward in how understandable I expected biology to be. I’d like to see it reviewed and voted on in the review.
I never would have thought biological systems are random, but spaghetti code isn't about randomness, it's about complex interdependence. This being said, the book looks really valuable-- even if can only help sort out the simpler parts of biology, that's quite a bit.
Note: the talk you mentioned was by Drew Endy and the electrical engineering colleague was the one and only Gerald Sussman of SICP fame (source: I don't remember but I'm very confident about being right).
Thanks. I'm also pretty sure you're right; I thought it was Endy but wasn't 100% sure because it's been a while.
No problem, also, in case it wasn't obvious based on the fact that I commented basically right after you posted this, I liked the post a lot and now plan to read this book ASAP.
You are correct. Please consider the difference between “understandable” and “ease of understanding”. Cheers. Drew.
I think that if you want to understand what structure might exist in neural networks and how comprehensible it's likely to be (which I do), looking at biology is a good place to start. This appears to be a pretty good overview of the structure of biological circuits, and hopefully gives one a taste of their degree of comprehensibility.
Thanks for this post!
I was excited to read the book reviewed just based on the first few sentences!
A large part of the reason this is interesting is that it bears on the alignment problem; if evolved mechanisms of complex systems tend to end up being comprehensible, alignment techniques that rely on inspecting the mind of an AGI become a lot easier to imagine than they currently are.
From a comment I made response to Rohin Shah on reasons for AI optimism.
One way of putting it is that in order for an agent to be recursively self-improving in any remotely intelligent way, it needs to be legible to itself. Even if we can't immediately understand its components in the same way that it does, it must necessarily provide us with descriptions of its own ways of understanding them, which we could then potentially co-opt.
Curated and popular this week