Followup to: Conjunction Fallacy
When a single experiment seems to show that subjects are guilty of some horrifying sinful bias - such as thinking that the proposition "Bill is an accountant who plays jazz" has a higher probability than "Bill is an accountant" - people may try to dismiss (not defy) the experimental data. Most commonly, by questioning whether the subjects interpreted the experimental instructions in some unexpected fashion - perhaps they misunderstood what you meant by "more probable".
Experiments are not beyond questioning; on the other hand, there should always exist some mountain of evidence which suffices to convince you. It's not impossible for researchers to make mistakes. It's also not impossible for experimental subjects to be really genuinely and truly biased. It happens. On both sides, it happens. We're all only human here.
If you think to extend a hand of charity toward experimental subjects, casting them in a better light, you should also consider thinking charitably of scientists. They're not stupid, you know. If you can see an alternative interpretation, they can see it too. This is especially important to keep in mind when you read about a bias and one or two illustrative experiments in a blog post. Yes, if the few experiments you saw were all the evidence, then indeed you might wonder. But you might also wonder if you're seeing all the evidence that supports the standard interpretation. Especially if the experiments have dates on them like "1982" and are prefaced with adjectives like "famous" or "classic".
So! This is a long post. It is a long post because nailing down a theory requires more experiments than the one or two vivid illustrations needed to merely explain. I am going to cite maybe one in twenty of the experiments that I've read about, which is maybe a hundredth of what's out there. For more information, see Tversky and Kahneman (1983) or Kahneman and Frederick (2002), both available online, from which this post is primarily drawn.
Here is (probably) the single most questioned experiment in the literature of heuristics and biases, which I reproduce here exactly as it appears in Tversky and Kahneman (1982):
Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.
Please rank the following statements by their probability, using 1 for the most probable and 8 for the least probable:
(5.2) Linda is a teacher in elementary school.
(3.3) Linda works in a bookstore and takes Yoga classes.
(2.1) Linda is active in the feminist movement. (F)
(3.1) Linda is a psychiatric social worker.
(5.4) Linda is a member of the League of Women Voters.
(6.2) Linda is a bank teller. (T)
(6.4) Linda is an insurance salesperson.
(4.1) Linda is a bank teller and is active in the feminist movement. (T & F)
(The numbers at the start of each line are the mean ranks of each proposition, lower being more probable.)
How do you know that subjects did not interpret "Linda is a bank teller" to mean "Linda is a bank teller and is not active in the feminist movement"? For one thing, dear readers, I offer the observation that most bank tellers, even the ones who participated in anti-nuclear demonstrations in college, are probably not active in the feminist movement. So, even so, Teller should rank above Teller & Feminist. You should be skeptical of your own objections, too; else it is disconfirmation bias. But the researchers did not stop with this observation; instead, in Tversky and Kahneman (1983), they created a between-subjects experiment in which either the conjunction or the two conjuncts were deleted. Thus, in the between-subjects version of the experiment, each subject saw either (T&F), or (T), but not both. With a total of five propositions ranked, the mean rank of (T&F) was 3.3 and the mean rank of (T) was 4.4, N=86. Thus, the fallacy is not due solely to interpreting "Linda is a bank teller" to mean "Linda is a bank teller and not active in the feminist movement."
Similarly, the experiment discussed yesterday used a between-subjects design (where each subject only saw one statement) to elicit lower probabilities for "A complete suspension of diplomatic relations between the USA and the Soviet Union, sometime in 1983" versus "A Russian invasion of Poland, and a complete suspension of diplomatic relations between the USA and the Soviet Union, sometime in 1983".
Another way of knowing whether subjects have misinterpreted an experiment is to ask the subjects directly. Also in Tversky and Kahneman (1983), a total of 103 medical internists (including 37 internists taking a postgraduate course at Harvard, and 66 internists with admitting privileges at New England Medical Center) were given problems like the following:
A 55-year-old woman had pulmonary embolism documented angiographically 10 days after a cholecstectomy. Please rank order the following in terms of the probability that they will be among the conditions experienced by the patient (use 1 for the most likely and 6 for the least likely). Naturally, the patient could experience more than one of these conditions.
- Dyspnea and hemiparesis
- Calf pain
- Pleuritic chest pain
- Syncope and tachycardia
- Hemiparesis
- Hemoptysis
As Tversky and Kahneman note, "The symptoms listed for each problem included one, denoted B, that was judged by our consulting physicians to be nonrepresentative of the patient's condition, and the conjunction of B with another highly representative symptom denoted A. In the above example of pulmonary embolism (blood clots in the lung), dyspnea (shortness of breath) is a typical symptom, whereas hemiparesis (partial paralysis) is very atypical."
In indirect tests, the mean ranks of A&B and B respectively were 2.8 and 4.3; in direct tests, they were 2.7 and 4.6. In direct tests, subjects ranked A&B above B between 73% to 100% of the time, with an average of 91%.
The experiment was designed to eliminate, in four ways, the possibility that subjects were interpreting B to mean "only B (and not A)". First, carefully wording the instructions: "...the probability that they will be among the conditions experienced by the patient", plus an explicit reminder, "the patient could experience more than one of these conditions". Second, by including indirect tests as a comparison. Third, the researchers afterward administered a questionnaire:
In assessing the probability that the patient described has a particular symptom X, did you assume that (check one):
X is the only symptom experienced by the patient?
X is among the symptoms experienced by the patient?
60 of 62 physicians, asked this question, checked the second answer.
Fourth and finally, as Tversky and Kahneman write, "An additional group of 24 physicians, mostly residents at Stanford Hospital, participated in a group discussion in which they were confronted with their conjunction fallacies in the same questionnaire. The respondents did not defend their answers, although some references were made to 'the nature of clinical experience.' Most participants appeared surprised and dismayed to have made an elementary error of reasoning."
A further experiment is also discussed in Tversky and Kahneman (1983) in which 93 subjects rated the probability that Bjorn Borg, a strong tennis player, would in the Wimbledon finals "win the match", "lose the first set", "lose the first set but win the match", and "win the first set but lose the match". The conjunction fallacy was expressed: "lose the first set but win the match" was ranked more probable than"lose the first set". Subjects were also asked to verify whether various strings of wins and losses would count as an extensional example of each case, and indeed, subjects were interpreting the cases as conjuncts which were satisfied iff both constituents were satisfied, and not interpreting them as material implications, conditional statements, or disjunctions; also, constituent B was not interpreted to exclude constituent A. The genius of this experiment was that researchers could directly test what subjects thought was the meaning of each proposition, ruling out a very large class of misunderstandings.
Does the conjunction fallacy arise because subjects misinterpret what is meant by "probability"? This can be excluded by offering students bets with payoffs. In addition to the colored dice discussed yesterday, subjects have been asked which possibility they would prefer to bet $10 on in the classic Linda experiment. This did reduce the incidence of the conjunction fallacy, but only to 56% (N=60), which is still more than half the students.
But the ultimate proof of the conjunction fallacy is also the most elegant. In the conventional interpretation of the Linda experiment, subjects substitute judgment of representativeness for judgment of probability: Their feelings of similarity between each of the propositions and Linda's description, determines how plausible it feels that each of the propositions is true of Linda. If this central theory is true, then the way in which the conjunction fallacy follows is obvious - Linda more closely resembles a feminist than a feminist bank teller, and more closely resembles a feminist bank teller than a bank teller. Well, that is our theory about what goes on in the experimental subjects minds, but how could we possibly know? We can't look inside their neural circuits - not yet! So how would you construct an experiment to directly test the standard model of the Linda experiment?
Very easily. You just take another group of experimental subjects, and ask them how much each of the propositions "resembles" Linda. This was done - see Kahneman and Frederick (2002) - and the correlation between representativeness and probability was nearly perfect. 0.99, in fact. Here's the (rather redundant) graph:
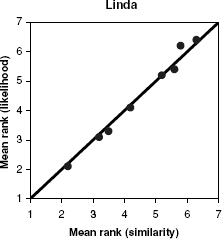
This has been replicated for numerous other experiments. For example, in the medical experiment described above, an independent group of 32 physicians from Stanford University was asked to rank each list of symptoms "by the degree to which they are representative of the clinical condition of the patient". The correlation between probability rank and representativeness rank exceeded 95% on each of the five tested medical problems.
Now, a correlation near 1 does not prove that subjects are substituting judgment of representativeness for judgment of probability. But if you want to claim that subjects are doing something else, I would like to hear the explanation for why the correlation comes out so close to 1. It will really take quite a complicated story to explain, not just why the subjects have an elaborate misunderstanding that produces an innocent and blameless conjunction fallacy, but also how it comes out to a completely coincidental correlation of nearly 1 with subjects' feeling of similarity. Across multiple experimental designs.
And we all know what happens to the probability of complicated stories: They go down when you add details to them.
Really, you know, sometimes people just make mistakes. And I'm not talking about the researchers here.
The conjunction fallacy is probably the single most questioned bias ever introduced, which means that it now ranks among the best replicated. The conventional interpretation has been nearly absolutely nailed down. Questioning, in science, calls forth answers.
I emphasize this, because it seems that when I talk about biases (especially to audiences not previously familiar with the field), a lot of people want to be charitable to experimental subjects. But it is not only experimental subjects who deserve charity. Scientists can also be unstupid. Someone else has already thought of your alternative interpretation. Someone else has already devised an experiment to test it. Maybe more than one. Maybe more than twenty.
A blank map is not a blank territory; if you don't know whether someone has tested it, that doesn't mean no one has tested it. This is not a hunter-gatherer tribe of two hundred people, where if you do not know a thing, then probably no one in your tribe knows. There are six billion people in the world, and no one can say with certitude that science does not know a thing; there is too much science. Absence of such evidence is only extremely weak evidence of absence. So do not mistake your ignorance of whether an alternative interpretation has been tested, for the positive knowledge that no one has tested it. Be charitable to scientists too. Do not say, "I bet what really happened was X", but ask, "Which experiments discriminated between the standard interpretation versus X?"
If it seems that I am driving this point home with a sledgehammer, well, yes, I guess I am. It does become a little frustrating, sometimes - to know about this overwhelming mountain of evidence from thousands of experiments, but other people have no clue that it exists. After all, if there are other experiments supporting the result, why haven't they heard of them? It's a small tribe, after all; surely they would have heard. By the same token, I have to make a conscious effort to remember that other people don't know about the evidence, and they aren't deliberately ignoring it in order to annoy me. Which is why it gets a little frustrating sometimes! We just aren't built for worlds of 6 billion people.
I'm not saying, of course, that people should stop asking questions. If you stop asking questions, you'll never find out about the mountains of experimental evidence. Faith is not understanding, only belief in a password. It is futile to believe in something, however fervently, when you don't really know what you're supposed to believe in. So I'm not saying that you should take it all on faith. I'm not saying to shut up. I'm not trying to make you feel guilty for asking questions.
I'm just saying, you should suspect the existence of other evidence, when a brief account of accepted science raises further questions in your mind. Not believe in that unseen evidence, just suspect its existence. The more so if it is a classic experiment with a standard interpretation. Ask a little more gently. Put less confidence in your brilliant new alternative hypothesis. Extend some charity to the researchers, too.
And above all, talk like a pirate. Arr!
Kahneman, D. and Frederick, S. 2002. Representativeness revisited: Attribute substitution in intuitive judgment. Pp 49-81 in Gilovich, T., Griffin, D. and Kahneman, D., eds. Heuristics and Biases: The Psychology of Intuitive Judgment. Cambridge University Press, Cambridge.
Tversky, A. and Kahneman, D. 1982. Judgments of and by representativeness. Pp 84-98 in Kahneman, D., Slovic, P., and Tversky, A., eds. Judgment under uncertainty: Heuristics and biases. New York: Cambridge University Press.
Tversky, A. and Kahneman, D. 1983. Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychological Review, 90: 293-315.