Seems worth noting that nostalgebraist published this post in June 2017, which was (for example) before Eliezer's post on toolbox thinking.
"Strong Bayesianism" is a strawman already addressed in Toolbox-thinking and Law-thinking. Excerpt:
I'm now going to badly stereotype this conversation in the form I feel like I've seen it many times previously, including e.g. in the discussion of p-values and frequentist statistics. On this stereotypical depiction, there is a dichotomy between the thinking of Msr. Toolbox and Msr. Lawful that goes like this:
Msr. Toolbox: "It's important to know how to use a broad variety of statistical tools and adapt them to context. The many ways of calculating p-values form one broad family of tools; any particular tool in the set has good uses and bad uses, depending on context and what exactly you do. Using likelihood ratios is an interesting statistical technique, and I'm sure it has its good uses in the right contexts. But it would be very surprising if that one weird trick was the best calculation to do in every paper and every circumstance. If you claim it is the universal best way, then I suspect you of blind idealism, insensitivity to context and nuance, ignorance of all the other tools in the toolbox, the sheer folly of callow youth. You only have a hammer and no real-world experience using screwdrivers, so you claim everything is a nail."
Msr. Lawful: "On complex problems we may not be able to compute exact Bayesian updates, but the math still describes the optimal update, in the same way that a Carnot cycle describes a thermodynamically ideal engine even if you can't build one. You are unlikely to find a superior viewpoint that makes some other update even more optimal than the Bayesian update, not without doing a great deal of fundamental math research and maybe not at all. We didn't choose that formalism arbitrarily! We have a very broad variety of coherence theorems all spotlighting the same central structure of probability theory, saying variations of 'If your behavior cannot be viewed as coherent with probability theory in sense X, you must be executing a dominated strategy and shooting off your foot in sense Y'."
I currently suspect that when Msr. Law talks like this, Msr. Toolbox hears "I prescribe to you the following recipe for your behavior, the Bayesian Update, which you ought to execute in every kind of circumstance."
This also appears to me to frequently turn into one of those awful durable forms of misunderstanding: Msr. Toolbox doesn't see what you could possibly be telling somebody to do with a "good" or "ideal" algorithm besides executing that algorithm.
I disagree that this answers my criticisms. In particular, my section 7 argues that it's practically unfeasible to even write down most practical belief / decision problems in the form that the Bayesian laws require, so "were the laws followed?" is generally not even a well-defined question.
To be a bit more precise, the framework with a complete hypothesis space is a bad model for the problems of interest. As I detailed in section 7, that framework assumes that our knowledge of hypotheses and the logical relations between hypotheses are specified "at the same time," i.e. when we know about a hypothesis we also know all its logical relations to all other hypotheses, and when we know (implicitly) about a logical relation we also have access (explicitly) to the hypotheses it relates. Not only is this false in many practical cases, I don't even know of any formalism that would allow us to call it "approximately true," or "true enough for the optimality theorems to carry over."
(N.B. as it happens, I don't think logical inductors fix this problem. But the very existence of logical induction as a research area shows that this is a problem. Either we care about the consequences of lacking logical omniscience, or we don't -- and apparently we do.)
It's sort of like quoting an optimality result given access to some oracle, when talking about a problem without access to that oracle. If the preconditions of a theorem are not met by the definition of a given decision problem, "meet those preconditions" cannot be part of a strategy for that problem. "Solve a different problem so you can use my theorem" is not a solution to the problem as stated.
Importantly, this is not just an issue of "we can't do perfect Bayes in practice, but if we were able, it'd be better." Obtaining the kind of knowledge representation assumed by the Bayesian laws has computational / resource costs, and in any real decision problem, we want to minimize these. If we're handed the "right" knowledge representation by a genie, fine, but if we are talking about choosing to generate it, that in itself is a decision with costs.
As a side point, I am also skeptical of some of the optimality results.
Let's zoom in on the oracle problem since it seems to be at the heart of the issue. You write:
It’s sort of like quoting an optimality result given access to some oracle, when talking about a problem without access to that oracle. If the preconditions of a theorem are not met by the definition of a given decision problem, “meet those preconditions” cannot be part of a strategy for that problem.
Here, it seems like you are doing something like interpreting a Msr. Law statement of the form "this Turing machine that has access to a halting oracle decides provability in PA" as a strategy for deciding provability in PA (as Eliezer's stereotype of Msr. Toolbox would). But the statement is true independent of whether it corresponds to a strategy for deciding provability in PA, and the statement is actually useful in formal logic. Obviously if you wanted to design an automated theorem prover for PA (applicable to some but not all practical problems) you would need a different strategy, and the fact that some specific Turing machine with access to a halting oracle decides provability in PA might or might not be relevant to your strategy.
I agree that applying Bayes' law as stated has resource costs and requires formally characterizing the hypothesis space, which is usually (but not always) hard in practice. The consequences of logical non-omniscience really matter, which is one reason that Bayesianism is not a complete epistemology.
I don't disagree with any of this. But if I understand correctly, you're only arguing against a very strong claim -- something like "Bayes-related results cannot possibly have general relevance for real decisions, even via 'indirect' paths that don't rely on viewing the real decisions in a Bayesian way."
I don't endorse that claim, and would find it very hard to argue for. I can imagine virtually any mathematical result playing some useful role in some hypothetical framework for real decisions (although I would be more surprised in some cases than others), and I can't see why Bayesian stuff should be less promising in that regard than any arbitrarily chosen piece of math. But "Bayes might be relevant, just like p-adic analysis might be relevant!" seems like damning with faint praise, given the more "direct" ambitions of Bayes as advocated by Jaynes and others.
Is there a specific "indirect" path for the relevance of Bayes that you have in mind here?
At a very rough guess, I think Bayesian thinking is helpful in 50-80% of nontrivial epistemic problems, more than p-adic analysis.
How might the law-type properties be indirectly relevant? Here are some cases:
-
In game theory it's pretty common to assume that the players are Bayesian about certain properties of the environment (see Bayesian game). Some generality is lost by doing so (after all, reasoning about non-Bayesian players might be useful), but, due to the complete class theorems, less generality is lost than one might think, since (with some caveats) all policies that are not strictly dominated are Bayesian policies with respect to some prior.
-
Sometimes likelihood ratios for different theories with respect to some test can be computed or approximated, e.g. in physics. Bayes' rule yields a relationship between the prior and posterior probability. Even in the absence of a way to determine what the right prior for the different theories is, if we can form a set of "plausible" priors (e.g. based on parsimony of the different theories and existing evidence), then Bayes' rule then yields a set of "plausible" posteriors, which can be narrow even if the set of plausible priors was broad.
-
Bayes' rule implies properties about belief updates such as conservation of expected evidence. If I expect my beliefs about some proposition to update in a particular direction in expectation, then I am expecting myself to violate Bayes' rule, which implies (by CCT) that, if the set of decision problems I might face is sufficiently rich, I expect my beliefs to yield some strictly dominated decision rule. It is not clear what to do in this state of knowledge, but the fact that my decision rule is currently strictly dominated does imply that I am somewhat likely to make better decisions if I think about the structure of my beliefs, and where the inconsistency is coming from. (In effect, noticing violations of Bayes' rule is a diagnostic tool similar to noticing violations of logical consistency)
I do think that some advocacy of Bayesianism has been overly ambitious, for the reasons stated in your post as well as those in this post. I think Jaynes in particular is overly ambitious in applications of Bayesianism, such as in recommending maximum-entropy models as an epistemological principle rather than as a useful tool. And I think this post by Eliezer (which you discussed) overreaches in a few ways. I still think that "Strong Bayesianism" as you defined it is a strawman, though there is some cluster in thoughtspace that could be called "Strong Bayesianism" that both of us would have disagreements with.
(as an aside, as far as I can tell, the entire section of Jaynes's Probability Theory: The Logic of Science is logically inconsistent)
If I had to run with the toolbox analogy, I would say that I think of Bayes not as a hammer but more of a 3D printer connected to a tool generator program.
Fasteners are designed to be used with a specific tool (nail & hammer, screw & screwdriver). Imagine, rather, you are trying to use an alien’s box of fasteners – none of them are designed to work with your tools. You might be able to find a tool which works ok, perhaps even pretty well. This is more like the case with a standard statistics toolbox.
If you enter the precise parameters of any fastener (even alien fasteners, whitworth bolts and torx screws) into your tool generator program then your 3D printer will produce the perfect tool for fastening it.
Depending on how well you need to do the job, you might use a similar tool and not bother 3D printing out a completely new tool every time. However, the fastening job will only be done as well as the tool you are using matches the perfect 3D printed tool. Understanding how your tool differs from the perfect tool helps you analyse how well fastened your work will be.
At times you may not know all of the parameters to put into the tool generator but estimating the parameters as best you can will still print (in expectation) a better tool than just picking the best one you can find in your toolbox.
This seems a little forced as an analogy but it’s the best I can come up with!
Don't have time to have a super long discussion, but I don't think this article really engaged with my beliefs about Bayesianism, or my model of Eliezer's belief about Bayesianism.
I can imagine that there are some people who think literally applying Bayesian probability diatributions to every modeling problem is a good choice, but I have not met any of them.
Whatever the actual knowledge representation inside our brains looks like, it doesn’t seem like it can be easily translated into the structure of “hypothesis space, logical relations, degrees of belief.”
That strikes me as the main issue when trying to apply Bayesian logic to real-world problems.
How so? The knowledge representation inside our brains probably doesn't look like real numbers either, but real numbers are still useful for real-world problems. Same with Bayesianism. It's normative: if Bayes says you should switch doors in the Monty Hall problem, then that's what you should do, even if your brain says no.
If I understand your objection correctly, it's one I tried to answer already in my post.
In short: Bayesianism is normative for problems to you can actually state in its formalism. This can be used as an argument for at least trying to state problems in its formalism, and I do think this is often a good idea; many of the examples in Jaynes' book show the value of doing this. But when the information you have actually does not fit the requirements of the formalism, you can only use it if you get more information (costly, sometimes impossible) or forget some of what you know to make the rest fit. I don't think Bayes normatively tells you to do those kinds of things, or at least that would require a type of argument different from the usual Dutch Books etc.
Using the word "brain" there was probably a mistake. This is only about brains insofar as it's about the knowledge actually available to you in some situation, and the same idea applies to the knowledge available to some robot you are building, or some agent in a hypothetical decision problem (so long as it is a problem with the same property, of not fitting well into the formalism without extra work or forgetting).
Yeah, I'm not saying Bayesianism solves all problems. But point 7b in your post still sounds weird to me. You assume a creature that can't see all logical consequences of hypotheses - that's fine. Then you make it realize new facts about logical consequences of hypotheses - that's also fine. But you also insist that the creature's updated probabilities must exactly match the original ones, or fit neatly between them. Why is that required? It seems to me that whatever the faults of "strong Bayesianism", this argument against it doesn't work.
You assume a creature that can't see all logical consequences of hypotheses [...] Then you make it realize new facts about logical consequences of hypotheses
This is not quite what is going on in section 7b. The agent isn't learning any new logical information. For instance, in jadagul's "US in 2100" example, all of the logical facts involved are things the agent already knows. " 'California is a US state in 2100' implies 'The US exists in 2100' " is not a new fact, it's something we already knew before running through the exercise.
My argument in 7b is not really about updating -- it's about whether probabilities can adequately capture the agent's knowledge, even at a single time.
This is in a context (typical of real decisions) where:
- the agent knows a huge number of logical facts, because it can correctly interpret hypotheses written in a logically transparent way, like "A and B," and because it knows lots of things about subsets in the world (like US / California)
- but, the agent doesn't have the time/memory to write down a "map" of every hypothesis connected by these facts (like a sigma-algebra). For example, you can read an arbitrary string of hypotheses "A and B and C and ..." and know that this implies "A", "A and C", etc., but you don't have in your mind a giant table containing every such construction.
So the agent can't assign credences/probabilities simultaneously to every hypothesis on that map. Instead, they have some sort of "credence generator" that can take in a hypothesis and output how plausible it seems, using heuristics. In their raw form, these outputs may not be real numbers (they will have an order, but may not have e.g. a metric).
If we want to use Bayes here, we need to turn these raw credences into probabilities. But remember, the agent knows a lot of logical facts, and via the probability axioms, these all translate to facts relating probabilities to one another. There may not be any mapping from raw credence-generator-output to probabilities that preserves all of these facts, and so the agent's probabilities will not be consistent.
To be more concrete about the "credence generator": I find that when I am asked to produce subjective probabilities, I am translating them from internal representations like
- Event A feels "very likely"
- Event B, which is not logically entailed by A or vice versa, feels "pretty likely"
- Event (A and B) feels "pretty likely"
If we demand that these map one-to-one to probabilities in any natural way, this is inconsistent. But I don't think it's inconsistent in itself; it just reflects that my heuristics have limited resolution. There isn't a conjunction fallacy here because I'm not treating these representations as probabilities -- but if I decide to do so, then I will have a conjunction fallacy! If I notice this happening, I can "plug the leak" by changing the probabilities, but I will expect to keep seeing new leaks, since I know so many logical facts, and thus there are so many consequences of the probability axioms that can fail to hold. And because I expect this to happen going forward, I am skeptical now that my reported probabilities reflect my actual beliefs -- not even approximately, since I expect to keep deriving very wrong things like an event being impossible instead of likely.
None of this is meant disapprove of using probability estimates to, say, make more grounded estimates of cost/benefit in real-world decisions. I do find that useful, but I think it is useful for a non-Bayesian reason: even if you don't demand a universal mapping from raw credences, you can get a lot of value out of saying things like "this decision isn't worth it unless you think P(A) > 97%", and then doing a one-time mapping of that back onto a raw credence, and this has a lot of pragmatic value even if you know the mappings will break down if you push them too hard.
If I notice this happening, I can “plug the leak” by changing the probabilities, but I will expect to keep seeing new leaks, since I know so many logical facts, and thus there are so many consequences of the probability axioms that can fail to hold. And because I expect this to happen going forward, I am skeptical now that my reported probabilities reflect my actual beliefs
Hmm, I think your "actual beliefs" are your betting odds at each moment, messy as they are. And what you call "plugging the leaks" seems to be Bayesian updating of your actual beliefs, which should converge for the usual reasons.
For example, if you haven't thought much about the connection between A, B and (A and B), you could say your feelings about these sentences haven't yet updated on the connection between them. (Think of it as a prior over sentences in sealed envelopes, ignorant of the sigma algebra structure.) Then you update and get closer to the truth. Does that make sense?
Two comments:
1. You seem to be suggesting that the standard Bayesian framework handles logical uncertainty as a special case. (Here we are not exactly "uncertain" about sentences, but we have to update on their truth from some prior that did not account for it, which amounts to the same thing.) If this were true, the research on handling logical uncertainty through new criteria and constructions would be superfluous. I haven't actually seen a proposal like this laid out in detail, but I think they've been proposed and found wanting, so I'll be skeptical at least until I'm shown the details of such a proposal.
(In particular, this would need to involve some notion of conditional probabilities like P(A | A => B), and perhaps priors like P(A => B), which are not a part of any treatment of Bayes I've seen.)
2. Even if this sort of thing does work in principle, it doesn't seem to help in the practical case at hand. We're now told to update on "noticing" A => B by using objects like P(A | A => B), but these too have to be guessed using heuristics (we don't have a map of them either), so it inherits the same problem it was introduced to solve.
I'm a bit confused by your mention of logical uncertainty. Isn't plain old probability sufficient for this problem? If A and B are statements about the world, and you have a prior over possible worlds (combinations of truth values for A and B), then probabilities like P(A ⇒ B) or P(A | A ⇒ B) seem well-defined to me. For example, P(A ⇒ B) = P(A and B) + P(not A).
Let's try to walk through the US and California example. At the start, you feel that A = "California will be a US state in 2100" and B = "US will exist in 2100" both have probability 98% and are independent, because you haven't thought much about the connection between them. Then you notice that A ⇒ B, so you remove the option "A and not B" from your prior and renormalize, leading to 97.96% for A and 99.96% for B. The probabilities are nudged apart, just like you wanted!
Of course you could say these numbers still look fake. The update for B was much stronger than the update for A, what's up with that? But that's because our prior was very ignorant to begin with. As we get more data, we'll converge on the truth. Bayes comes out of this exercise looking pretty good, if you ask me.
Ah, yeah, you're right that it's possible to do this. I'm used to thinking in the Kolmogorov picture, and keep forgetting that in the Jaynesian propositional logic picture you can treat material conditionals as contingent facts. In fact, I went through the process of realizing this in a similar argument about the same post a while ago, and then forgot about it in the meantime!
That said, I am not sure what this procedure has to recommend it, besides that it is possible and (technically) Bayesian. The starting prior, with independence, does not really reflect our state of knowledge at any time, even at the time before we have "noticed" the implication(s). For, if we actually write down that prior, we have an entry in every cell of the truth table, and if we inspect each of those cells and think "do I really believe this?", we cannot answer the question without asking whether we know facts such as A => B -- at which point we notice the implication!
It seems more accurate to say that, before we consider the connection of A to B, those cells are "not even filled in." The independence prior is not somehow logically agnostic; it assigns a specific probability to the conditional, just as our posterior does, except that in the prior that probability is, wrongly, not one.
Okay, one might say, but can't this still be a good enough place to start, allowing us to converge eventually? I'm actually unsure about this, because (see below) the logical updates tend to push the probabilities of the "ends" of a logical chain further towards 0 and 1; at any finite time the distribution obeys Cromwell's Rule, but whether it converges to the truth might depend on the way in which we take the limit over logical and empirical updates (supposing we do arbitrarily many of each type as time goes on).
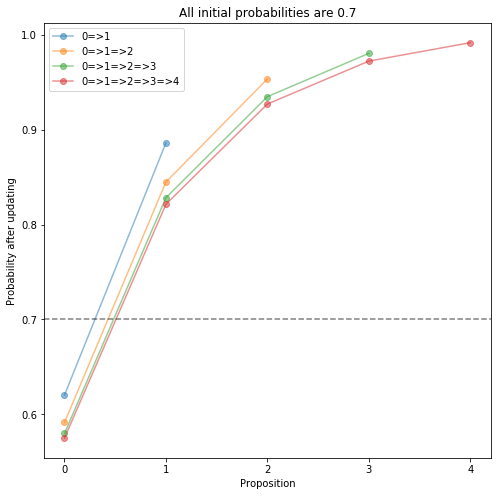
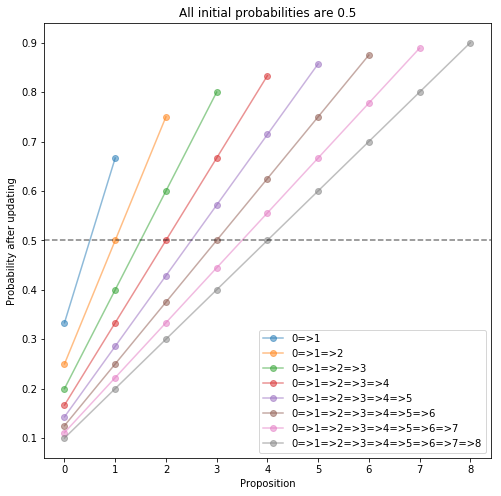
I got curious about this and wrote some code to do these updates with arbitrary numbers of variables and arbitrary conditionals. What I found is that as we consider longer chains A => B => C => ..., the propositions at one end get pushed to 1 or 0, and we don't need very long chains for this to get extreme. With all starting probabilities set to 0.7 and three variables 0 => 1 => 2, the probability of variable 2 is 0.95; with five variables the probability of the last one is 0.99 (see the plot below). With ten variables, the last one reaches 0.99988. We can easily come up with long chains in the California example or similar, and following this procedure would lead us to absurdly extreme confidence in such examples.
I've also given a second plot below, where all the starting probabilities are 0.5. This shows that the growing confidence does not rely on an initial hunch one way or the other; simply updating on the logical relationships from initial neutrality (plus independences) pushes us to high confidence about the ends of the chain.
Yeah, if the evidence you see (including logical evidence) is filtered by your adversary, but you treat it as coming from an impartial process, you can be made to believe extreme stuff. That problem doesn't seem to be specific to Bayes, or at least I can't imagine any other method that would be immune to it.
Here's a simple model: the adversary flips a coin ten times and reveals some of the results to you, which happen to be all heads. You believe that the choice of which results to reveal is independent of the results themselves, but in fact the adversary only reveals heads. So your beliefs about the coin's bias are predictably pushed toward heads.
The usual Bayesian answer is that you should have nonzero probability that evidence is revealed adversarially. Then over time that probability will dominate. Similarly in our problem, you should have nonzero probability that someone is coming up with intermediate statements between A and Z and showing you only those, instead of other statements that would appear elsewhere in the graph and temper your beliefs a bit. That makes the model complicated enough that I can't work it out on a napkin anymore, but I'm pretty sure it's the only way.
To quote Abram Demski in “All Mathematicians are Trollable”:
The main concern is not so much whether GLS-coherent mathematicians are trollable as whether they are trolling themselves. Vulnerability to an external agent is somewhat concerning, but the existence of misleading proof-orderings brings up the question: are there principles we need to follow when deciding what proofs to look at next, to avoid misleading ourselves?
My concern is not with the dangers of an actual adversary, it’s with the wild oscillations and extreme confidences that can arise even when logical facts arrive in a “fair” way, so long as it is still possible to get unlucky and experience a “clump” of successive observations that push P(A) way up or down.
We should expect such clumps sometimes unless the observation order is somehow specially chosen to discourage them, say via the kind of “principles” Demski wonders about.
One can also prevent observation order from mattering by doing what the Eisenstat prior does: adopt an observation model that does not treat logical observations as coming from some fixed underlying reality (so that learning “B or ~A” rules out some ways A could have been true), but as consistency-constrained samples from a fixed distribution. This works as far as it goes, but is hard to reconcile with common intuitions about how e.g. P=NP is unlikely because so many “ways it could have been true” have failed (Scott Aaronson has a post about this somewhere, arguing against Lubos Motl who seems to think like the Eisenstat prior), and more generally with any kind of mathematical intuition — or with the simple fact that the implications of axioms are fixed in advance and not determined dynamically as we observe them. Moreover, I don’t know of any way to (approximately) apply this model in real-world decisions, although maybe someone will come up with one.
This is all to say that I don’t think there is (yet) any standard Bayesian answer to the problem of self-trollability. It’s a serious problem and one at the very edge of current understanding, with only some partial stabs at solutions available.
Extended criticism of "Bayesianism" as discussed on LW. An excerpt from the first section of the post:
Contents of the post:
0. What is “Bayesianism”?
1. What is the Bayesian machinery?
1a. Synchronic Bayesian machinery
1b. Diachronic Bayesian machinery
3. What is Bayes’ Theorem?
4. How does the Bayesian machinery relate to the more classical approach to statistics?
5. Why is the Bayesian machinery supposed to be so great?
6. Get to the goddamn point already. What’s wrong with Bayesianism?
7. The problem of ignored hypotheses with known relations
7b. Okay, but why is this a problem?
8. The problem of new ideas
8b. The natural selection analogy
9. Where do priors come from?
10. It’s just regularization, dude
11. Bayesian “Occam factors”