Don't have time for a real response. Quickly and ramblingly:
1) The point of Bayesianism isn't that there's a toolbox of known algorithms like max-entropy methods which are supposed to work for everything. The point of Bayesianism is to provide a coherent background epistemology which underlies everything; when a frequentist algorithm works, there's supposed to be a Bayesian explanation of why it works. I have said this before many times but it seems to be a "resistant concept" which simply cannot sink in for many people.
2) I did initially try to wade into the math of the linear problem (and wonder if I'm the only one who did so, unless others spotted the x-y inversion but didn't say anything), trying to figure out how I would solve it even though that wasn't really relevant for reasons of (1), but found that the exact original problem specified may be NP-hard according to Wikipedia, much as my instincts said it should be. And if we're allowed approximate answers then yes, throwing a standard L1-norm algorithm at it is pretty much what I would try, though I might also try some form of expectation-maximization using the standard Bayesian L2 technique and repeatedly tr...
when a frequentist algorithm works, there's supposed to be a Bayesian explanation of why it works. I have said this before many times but it seems to be a "resistant concept" which simply cannot sink in for many people.
Perhaps the reason this is not sinking in for many people is because it is not true.
Bayes assumes you can write down your prior, your likelihood and your posterior. That is what we need to get Bayes theorem to work. If you are working with a statistical model where this is not possible*, you cannot really use the standard Bayesian story, yet there still exist ways of attacking the problem.
(*) Of course, "not possible in principle" is different from "we don't know how to yet." In either case, I am not really sure what the point of an official Bayesian epistemology explanation would be.
This idea that there is a standard Bayesian explanation for All The Things seems very strange to me. Andrew Gelman has a post on his blog about how to define "identifiability" if you are a Bayesian:
(http://andrewgelman.com/2014/02/12/think-identifiability-bayesian-inference/)
This is apparently a tricky (or not useful) concept to define ...
I wouldn't say "no Bayesian explanation," but perhaps "a Bayesian explanation is unknown to me, nor do I see how this explanation would illuminate anything." But yes, I gave an example elsewhere in this thread. The FCI algorithm for learning graph structure in the non-parametric setting with continuous valued variables, where the correct underlying model has the following independence structure:
A is independent of B and C is independent of D (and nothing else is true).
Since I (and to my knowledge everyone else) do not know how to write the likelihood for this model, I don't know how to set up the standard Bayesian story here.
Eliezer,
The point of Bayesianism is to provide a coherent background epistemology which underlies everything; when a frequentist algorithm works, there's supposed to be a Bayesian explanation of why it works. I have said this before many times but it seems to be a "resistant concept" which simply cannot sink in for many people.
First, I object to the labeling of Bayesian explanations as a "resistant concept". I think it's not only uncharitable but also wrong. I started out with exactly the viewpoint that everything should be explained in terms of Bayes (see one of my earliest and most-viewed blog posts if you don't believe me). I moved away from this viewpoint slowly as the result of accumulated evidence that this is not the most productive lens through which to view the world.
More to the point: why is it that you think that everything should have a Bayesian explanation? One of the most-cited reasons why Bayes should be an empistemic ideal is the various "optimality" / Dutch book theorems, which I've already argued against in this post. Do you accept the rebuttals I gave, or disagree with them?
My guess is that you would still be in favor of Bayes as...
My guess is that you would still be in favor of Bayes as a normative standard of epistemology even if you rejected Dutch book arguments, and the reason why you like it is because you feel like it has been useful for solving a large number of problems.
Um, nope. What it would really take to change my mind about Bayes is seeing a refutation of Dutch Book and Cox's Theorem and Von Neumann-Morgenstern and the complete class theorem , combined with seeing some alternative epistemology (e.g. Dempster-Shafer) not turn out to completely blow up when subjected to the same kind of scrutiny as Bayesianism (the way DS brackets almost immediately go to [0-1] and fuzzy logic turned out to be useless etc.)
Neural nets have been useful for solving a large number of problems. It doesn't make them good epistemology. It doesn't make them a plausible candidate for "Yes, this is how you need to organize your thinking about your AI's thinking and if you don't your AI will explode".
some of which Bayesian statistics cannot solve, as I have demonstrated in this post.
I am afraid that your demonstration was not stated sufficiently precisely for me to criticize. This seems like the sort of...
Your criticism of Dutch Book is that it doesn't seem to you useful to add anti-Dutch-book checkers to your toolbox. My support of Dutch Book is that if something inherently produces Dutch Books then it can't be the right epistemological principle because clearly some of its answers must be wrong even in the limit of well-calibrated prior knowledge and unbounded computing power.
The complete class theorem I understand least of the set, and it's probably not very much entwined with my true rejection so it would be logically rude to lead you on here. Again, though, the point that every local optimum is Bayesian tells us something about non-Bayesian rules producing intrinsically wrong answers. If I believed your criticism, I think it would be forceful; I could accept a world in which for every pair of a rational plan with a world, there is an irrational plan which does better in that world, but no plausible way for a cognitive algorithm to output that irrational plan - the plans which are equivalent of "Just buy the winning lottery ticket, and you'll make more money!" I can imagine being shown that the complete class theorem demonstrates only an "unfair" superior...
I don't have a technical basis for thinking this, but I'm beginning to suspect that as time goes on, more and more frequentist methods will be proven to be equivalent or good approximations to the ideal Bayesian approach. If that happens, (Edit: Hypothetical) Bayesians who refused to use those methods on ideological grounds would look kind of silly in hindsight, as if relativistic physics came first and a bunch of engineers refused to use Newtonian equations for decades until someone proved that they approximate the truth well at low speeds.
Who are these mysterious straw Bayesians who refuse to use algorithms that work well and could easily turn out to have a good explanation later? Bayes is epistemological background not a toolbox of algorithms.
After a careful rereading of http://lesswrong.com/lw/mt/beautiful_probability/, the 747 analogy suggests that, once you understand the difference between an epistemological background and a toolbox, it might be a good idea to use the toolbox. But I didn't really read it that way the first time, so I imagine others might have made a similar mistake. I'll edit my post to make the straw Bayesians hypothetical, to make it clear that I'm making a point to other LW readers rather than criticizing a class of practicing statisticians.
Great post! It would be great if you had cites for various folks claiming myth k. Some of these sound unbelievable!
"Frequentist methods need to assume their model is correct."
This one is hilarious. Does anyone say this? Multiply robust methods (Robins/Rotnitzky/et al) aren't exactly Bayesian, and their entire point is that you can get a giant piece of the likelihood arbitrarily wrong and your estimator is still consistent.
I'll add some here, maybe others can chime in as well. Some of these are quotes of my past self, is that fair?
4: Share likelihood ratios, not posterior beliefs
5: They assume they have perfect information about experimental setups and likelihood ratios
I am confused about your use of the word optimal. In particular in the sentences
Bayesian methods are optimal (except for computational considerations).
and
Bayesian methods are locally optimal, not global optimal.
are you talking about the same sort of 'optimal'? From wikipedia (here and here) I found the rigorous definition of the word 'optimal' in the second sentence, which can be written in terms of your utility function (a decision rule is optimal if there is no other decision rule which will always give you at least as much utility and in at least one world will give you more utility).
Also I agree with many of your myths, namely 3,8,9 and 11. I was rather surprised to see that these things even needed to be mentioned, I don't see why making good trade-offs between truth and computation time should be 'simple' (3), as you mentioned the frequentist tests are chosen precisely with robustness in mind (8), bad science is more than getting your statistics wrong (9) (small sidenote: while it might be true that scientists can get confused by frequentist statistics, which might corrupt their science, I don't think the problem would be smaller when using a different form of statist...
I've been thinking about what program, exactly, is being defended here, and I think a good name for it might be "prior-less learning". To me, all procedures under the prior-less umbrella have a "minimax optimality" feel to them. Some approaches search for explicitly minimax-optimal procedures; but even more broadly, all such approaches aim to secure guarantees (possibly probabilistic) that the worst-case performance of a given procedure is as limited as possible within some contemplated set of possible states of the world. I have a couple of things to say about such ideas.
First, for the non-probabilistically guaranteed methods: these are relatively few and far between, and for any such procedure it must be ensured that the loss that is being guaranteed is relevant to the problem at hand. That said, there is only one possible objection to them, and it is the same as one of my objections to prior-less probabilistically guaranteed methods. That objection applies generically to the minimaxity of the prior-less learning program: when strong prior information exists but is difficult to incorporate into the method, the results of the method can "leave money on th...
Regarding myth 5 and the online learning, I don't think the average regret bound is as awesome as you claim. The bound is square root( (log n) / T). But if there are really no structural assumptions, then you should be considering all possible models, and the number of possible models for T rounds is exponential in T, so the bound ends up being 1, which is the worst possible average regret using any strategy. With no assumptions of structure, there is no meaningful guarantee on the real accuracy of the method.
The thing that is awesome about the bounds guarantee is that if you assume some structure, and choose a subset of possible models based on that structure, you know you get increased accuracy if your structural assumptions hold.
So this method doesn't really avoid relying on structural assumptions, it just punts the question of which structural assumption to make to the choice of models to run the method over. This is pretty much the same as Bayesian methods putting the structural assumptions in the prior, and it seems that choosing a collection of models is an approximation of choosing a prior, though less powerful because instead of assigning models probabilities in a continuous range, it just either includes the model or doesn't.
What you have labelled Cox's theorem is not Cox's theorem; it's some version of the Dutch book argument and/or Savage's theorem. Cox's theorem is more like this. (I am the author of those blog posts.)
Also, you've misstated the complete class theorem -- it's actually weaker than you claim. It says that every estimator is either risk-equivalent to some Bayesian minimum posterior expected loss estimator (BMPELE) or has worse risk in at least one possible world. Conversely, no non-BMPELE risk-dominates any BMPELE. (Here "risk" is statistical jargon for expected loss, where the expectation is taken with respect to the sampling distribution.)
I assume you mean in the "infer u" problem? Or am I missing something?
Also, is there a good real-world problem which this reflects?
The biggest Bayesian objection to so-called "classical" statistics -- p-values and confidence intervals, not the online-learning stuff with non-probabilistic guarantees -- is that they provide the correct answer to the wrong question. For example, confidence intervals are defined as random intervals with certain properties under the sampling distribution. These properties are "pre-data" guarantees; the confidence interval procedure offers no guarantees to the one specific interval one calculates from the actual realized data one observes.
Nice post, but it would be preferable if you provided references, especially for the mathematical claims.
Great post! I learned a lot.
I agree that "frequentists do it wrong so often" is more because science is done by humans than due to any flaw in frequentist techniques. I also share your expectation that increased popularity of Bayesian techniques with more moving parts is likely to lead to more, not less, motivated selective use.
The online learning example, though, seems very unambitious in its loss function. Ideally you'd do better than any individual estimator in the underlying data. Let's say I was trying to use answers on the SAT test to predi...
...On the other hand, an argument I hear is that Bayesian methods make their assumptions explicit because they have an explicit prior. If I were to write this as an assumption and guarantee, I would write:
Assumption: The data were generated from the prior.
Guarantee: I will perform at least as well as any other method.
While I agree that this is an assumption and guarantee of Bayesian methods, there are two problems that I have with drawing the conclusion that “Bayesian methods make their assumptions explicit”. The first is that it can often be very difficult
Where is all this "local optimum" / "global optimum" stuff coming from? While I'm not familiar with the complete class theorem, going by the rough statement given in the article... local vs. global optima is just not the issue here, and is entirely the wrong language to talk about this here?
That is to say, talking about local maximum requires that A. things are being measured wrt some total order (though I suppose could be relaxed to a partial order, but you'd have to be clear whether you meant "locally maximum" or just "...
One useful definition of Bayesian vs Frequentist that I've found is the following. Suppose you run an experiment; you have a hypothesis and you gather some data.
- if you try to obtain the probability of the data, given your hypothesis (treating the hypothesis as fixed), then you're doing it the frequentist way
- if you try to obtain the probability of the hypothesis, given the data you have, then you're doing it the Bayesian way.
I'm not sure whether this view holds up to criticism, but if so, I sure find the latter much more interesting than the former.
This seems analogous to the situation where there’s some quant at Jane Street, and they’re about to run code that will make thousands of dollars trading stocks, and someone comes up to them and says “Wait! You should add checks to your code to make sure that no subset of your trades will lose you money!”
I would be quite surprised if Wall Street quant firms didn't use unit tests of this sort before letting a new algorithm play with real money. And in fact, I can imagine a promising-sounding algorithm flaming out by making a cycle of Dutch-booked trades...
I am deeply confused by your statement that the complete class theorem only implies that Bayesian techniques are locally optimal. If for EVERY non-Bayesian method there's a better Bayesian method, then the globally optimal technique must be a Bayesian method.
Excellent post.
I especially love the concrete and specific example in #3
Mostly whenever you see people discuss something "Bayesian" or "frequentist" here, or updates, it just makes you appreciate the fact that Gladwell made up a new term for what-ever he intuited the eigenvalue was, that was not what eigenvalue is.
What he doesn't tell you is that myth 5 (online learning) applies McDiarmid's_inequality to derive the more precise bound
%20%14\le%20R_{emp}(f_n)%20+%20\sqrt{log(N)%20+%20log(1/\delta)\over{2n}}%0A)
R is the real regret, R_emp the empirical regret (measured) and delta is the variance above.
This is derived e.g. in Introduction to Statistical Learning Theory, 2004, Bousquet et al
And you can get even better convergence if you know more about the distribution e.g. its VC dimension (roughly how difficult it is to decompose).
EDIT: LaTeX math in comment fixed.
The view of maximum entropy you are providing is basically the same as what physicists would present. If your function phi were the system Hamiltonian (and the expectation of phi, the energy), the function q you set up is the Boltzmann distribution, etc.
If its different than the view presented by Jaynes, I'm not sure I see why.
(Myth 5) Online learning: Online learning and online convex optimization
Can you be more specific about which result(s) within the 84 pages of this document substantiate your claims? Actually it would be better to have a reference to a result in a paper in a peer reviewed journal.
As I understand it, the big difference between Bayesian and frequentist methods is in what they output. A frequentist methods gives you a single prediction $z_t$, while a Bayesian method gives you a probability distribution over the predictions, $p(z_t)$. If your immediate goal is to minimize a known (or approximable) loss function, then frequentist methods work great. If you want to combine the predictions with other things as part of a larger whole, then you really need to know the uncertainty of your prediction, and ideally you need the entire distribut...
I've come to the conclusion that the strength and weakness of the Bayesian method is that it's simultaneously your experimental procedure and your personal decision-making method (given a utility function, that is). This makes it more powerful, but can also make getting a good answer more demanding.
The strength is that it makes mathematical things that are done informally in frequentism. This is the way in which Bayes makes assumptions explicit that frequentism hides. For example, suppose a frequentist does an experiment that shows that broccoli causes can...
Thanks for the thought-provoking post. How would you answer this criticism of the frequentist paradigm:
- Frequentist methods cannot make statements about actual data, only about abstract properties of the data.
For example, suppose I generated a data set of 1000 samples by weighing a bunch of people. So I just have 1000 numbers x1, x2... x1000 representing their weight in kilograms. Given this data set, frequentist analysis can make various claims about abstract properties such as its mean or variance or whether it could possibly have been drawn from a ...
[Highlights for the busy: de-bunking standard "Bayes is optimal" arguments; frequentist Solomonoff induction; and a description of the online learning framework. Note: cross-posted from my blog.]
Short summary. This essay makes many points, each of which I think is worth reading, but if you are only going to understand one point I think it should be “Myth 5″ below, which describes the online learning framework as a response to the claim that frequentist methods need to make strong modeling assumptions. Among other things, online learning allows me to perform the following remarkable feat: if I’m betting on horses, and I get to place bets after watching other people bet but before seeing which horse wins the race, then I can guarantee that after a relatively small number of races, I will do almost as well overall as the best other person, even if the number of other people is very large (say, 1 billion), and their performance is correlated in complicated ways.
If you’re only going to understand two points, then also read about the frequentist version of Solomonoff induction, which is described in “Myth 6″.
Main article. I’ve already written one essay on Bayesian vs. frequentist statistics. In that essay, I argued for a balanced, pragmatic approach in which we think of the two families of methods as a collection of tools to be used as appropriate. Since I’m currently feeling contrarian, this essay will be far less balanced and will argue explicitly against Bayesian methods and in favor of frequentist methods. I hope this will be forgiven as so much other writing goes in the opposite direction of unabashedly defending Bayes. I should note that this essay is partially inspired by some of Cosma Shalizi’s blog posts, such as this one.
This essay will start by listing a series of myths, then debunk them one-by-one. My main motivation for this is that Bayesian approaches seem to be highly popularized, to the point that one may get the impression that they are the uncontroversially superior method of doing statistics. I actually think the opposite is true: I think most statisticans would for the most part defend frequentist methods, although there are also many departments that are decidedly Bayesian (e.g. many places in England, as well as some U.S. universities like Columbia). I have a lot of respect for many of the people at these universities, such as Andrew Gelman and Philip Dawid, but I worry that many of the other proponents of Bayes (most of them non-statisticians) tend to oversell Bayesian methods or undersell alternative methodologies.
If you are like me from, say, two years ago, you are firmly convinced that Bayesian methods are superior and that you have knockdown arguments in favor of this. If this is the case, then I hope this essay will give you an experience that I myself found life-altering: the experience of having a way of thinking that seemed unquestionably true slowly dissolve into just one of many imperfect models of reality. This experience helped me gain more explicit appreciation for the skill of viewing the world from many different angles, and of distinguishing between a very successful paradigm and reality.
If you are not like me, then you may have had the experience of bringing up one of many reasonable objections to normative Bayesian epistemology, and having it shot down by one of many “standard” arguments that seem wrong but not for easy-to-articulate reasons. I hope to lend some reprieve to those of you in this camp, by providing a collection of “standard” replies to these standard arguments.
I will start with the myths (and responses) that I think will require the least technical background and be most interesting to a general audience. Toward the end, I deal with some attacks on frequentist methods that I believe amount to technical claims that are demonstrably false; doing so involves more math. Also, I should note that for the sake of simplicity I’ve labeled everything that is non-Bayesian as a “frequentist” method, even though I think there’s actually a fair amount of variation among these methods, although also a fair amount of overlap (e.g. I’m throwing in statistical learning theory with minimax estimation, which certainly have a lot of overlap in ideas but were also in some sense developed by different communities).
The Myths:
Myth 1: Bayesian methods are optimal. Presumably when most people say this they are thinking of either Dutch-booking or the complete class theorem. Roughly what these say are the following:
Dutch-book argument: Every coherent set of beliefs can be modeled as a subjective probability distribution. (Roughly, coherent means “unable to be Dutch-booked”.)
Complete class theorem: Every non-Bayesian method is worse than some Bayesian method (in the sense of performing deterministically at least as poorly in every possible world).
Let’s unpack both of these. My high-level argument regarding Dutch books is that I would much rather spend my time trying to correspond with reality than trying to be internally consistent. More concretely, the Dutch-book argument says that if for every bet you force me to take one side or the other, then unless I’m Bayesian there’s a collection of bets that will cause me to lose money for sure. I don’t find this very compelling. This seems analogous to the situation where there’s some quant at Jane Street, and they’re about to run code that will make thousands of dollars trading stocks, and someone comes up to them and says “Wait! You should add checks to your code to make sure that no subset of your trades will lose you money!” This just doesn’t seem worth the quant’s time, it will slow down the code substantially, and instead the quant should be writing the next program to make thousands more dollars. This is basically what dutch-booking arguments seem like to me.
Moving on, the complete class theorem says that for any decision rule, I can do better by replacing it with some Bayesian decision rule. But this injunction is not useful in practice, because it doesn’t say anything about which decision rule I should replace it with. Of course, if you hand me a decision rule and give me infinite computational resources, then I can hand you back a Bayesian method that will perform better. But it still might not perform well. All the complete class theorem says is that every local optimum is Bayesan. To be a useful theory of epistemology, I need a prescription for how, in the first place, I am to arrive at a good decision rule, not just a locally optimal one. And this is something that frequentist methods do provide, to a far greater extent than Bayesian methods (for instance by using minimax decision rules such as the maximum-entropy example given later). Note also that many frequentist methods do correspond to a Bayesian method for some appropriately chosen prior. But the crucial point is that the frequentist told me how to pick a prior I would be happy with (also, many frequentist methods don’t correspond to a Bayesian method for any choice of prior; they nevertheless often perform quite well).
Myth 2: Bayesian methods are optimal except for computational considerations. We already covered this in the previous point under the complete class theorem, but to re-iterate: Bayesian methods are locally optimal, not global optimal. Identifying all the local optima is very different from knowing which of them is the global optimum. I would much rather have someone hand me something that wasn’t a local optimum but was close to the global optimum, than something that was a local optimum but was far from the global optimum.
Myth 3: We can deal with computational constraints simply by making approximations to Bayes. I have rarely seen this born out in practice. Here’s a challenge: suppose I give you data generated in the following way. There are a collection of vectors ,
, 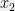 ,
,  ,
,  , each with
, each with  coordinates. I generate outputs
coordinates. I generate outputs  ,
,  ,
,  ,
,  in the following way. First I globally select
in the following way. First I globally select  of the
of the  coordinates uniformly at random, then I select a fixed vector
coordinates uniformly at random, then I select a fixed vector  such that those
such that those  coordinates are drawn from i.i.d. Gaussians and the rest of the coordinates are zero. Now I set
coordinates are drawn from i.i.d. Gaussians and the rest of the coordinates are zero. Now I set 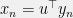 (i.e.
(i.e. 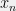 is the dot product of
is the dot product of  with
with  ). You are given
). You are given  and
and 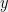 , and your job is to infer
, and your job is to infer  . This is a completely well-specified problem, the only task remaining is computational. I know people who have solved this problem using Bayesan methods with approximate inference. I have respect for these people, because doing so is no easy task. I think very few of them would say that “we can just approximate Bayesian updating and be fine”. (Also, this particular problem can be solved trivially with frequentist methods.)
. This is a completely well-specified problem, the only task remaining is computational. I know people who have solved this problem using Bayesan methods with approximate inference. I have respect for these people, because doing so is no easy task. I think very few of them would say that “we can just approximate Bayesian updating and be fine”. (Also, this particular problem can be solved trivially with frequentist methods.)
A particularly egregious example of this is when people talk about “computable approximations to Solomonoff induction” or “computable approximations to AIXI” as if such notions were meaningful.
Myth 4: the prior isn’t a big deal because Bayesians can always share likelihood ratios. Putting aside the practical issue that there would in general be an infinite number of likelihood ratios to share, there is the larger issue that for any hypothesis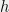 , there is also the hypothesis
, there is also the hypothesis 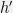 that matches
that matches 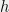 exactly up to now, and then predicts the opposite of
exactly up to now, and then predicts the opposite of 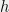 at all points in the future. You have to constrain model complexity at some point, the question is about how. To put this another way, sharing my likelihood ratios without also constraining model complexity (by focusing on a subset of all logically possible hypotheses) would be equivalent to just sharing all sensory data I’ve ever accrued in my life. To the extent that such a notion is even possible, I certainly don’t need to be a Bayesian to do such a thing.
at all points in the future. You have to constrain model complexity at some point, the question is about how. To put this another way, sharing my likelihood ratios without also constraining model complexity (by focusing on a subset of all logically possible hypotheses) would be equivalent to just sharing all sensory data I’ve ever accrued in my life. To the extent that such a notion is even possible, I certainly don’t need to be a Bayesian to do such a thing.
Myth 5: frequentist methods need to assume their model is correct or that the data are i.i.d. Understanding the content of this section is the most important single insight to gain from this essay. For some reason it’s assumed that frequentist methods need to make strong assumptions (such as Gaussianity), whereas Bayesian methods are somehow immune to this. In reality, the opposite is true. While there are many beautiful and deep frequentist formalisms that answer this, I will choose to focus on one of my favorite, which is online learning.
To explain the online learning framework, let us suppose that our data are . We don’t observe
. We don’t observe 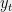 until after making a prediction
until after making a prediction 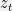 of what
of what 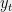 will be, and then we receive a penalty
will be, and then we receive a penalty  based on how incorrect we were. So we can think of this as receiving prediction problems one-by-one, and in particular we make no assumptions about the relationship between the different problems; they could be i.i.d., they could be positively correlated, they could be anti-correlated, they could even be adversarially chosen.
based on how incorrect we were. So we can think of this as receiving prediction problems one-by-one, and in particular we make no assumptions about the relationship between the different problems; they could be i.i.d., they could be positively correlated, they could be anti-correlated, they could even be adversarially chosen.
As a running example, suppose that I’m betting on horses and before each race there are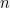 other people who give me advice on which horse to bet on. I know nothing about horses, so based on this advice I’d like to devise a good betting strategy. In this case,
other people who give me advice on which horse to bet on. I know nothing about horses, so based on this advice I’d like to devise a good betting strategy. In this case, 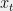 would be the
would be the 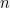 bets that each of the other people recommend,
bets that each of the other people recommend, 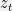 would be the horse that I actually bet on, and
would be the horse that I actually bet on, and 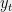 would be the horse that actually wins the race. Then, supposing that
would be the horse that actually wins the race. Then, supposing that  (i.e., the horse I bet on actually wins),
(i.e., the horse I bet on actually wins),  is the negative of the payoff from correctly betting on that horse. Otherwise, if the horse I bet on doesn’t win,
is the negative of the payoff from correctly betting on that horse. Otherwise, if the horse I bet on doesn’t win,  is the cost I had to pay to place the bet.
is the cost I had to pay to place the bet.
If I’m in this setting, what guarantee can I hope for? I might ask for an algorithm that is guaranteed to make good bets — but this seems impossible unless the people advising me actually know something about horses. Or, at the very least, one of the people advising me knows something. Motivated by this, I define my regret to be the difference between my penalty and the penalty of the best of the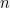 people (note that I only have access to the latter after all
people (note that I only have access to the latter after all 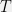 rounds of betting). More formally, given a class
rounds of betting). More formally, given a class 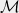 of predictors
of predictors  , I define
, I define
In this case,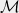 would have size
would have size 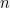 and the
and the 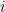 th predictor would just always follow the advice of person
th predictor would just always follow the advice of person 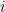 . The regret is then how much worse I do on average than the best expert. A remarkable fact is that, in this case, there is a strategy such that
. The regret is then how much worse I do on average than the best expert. A remarkable fact is that, in this case, there is a strategy such that 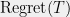 shrinks at a rate of
shrinks at a rate of 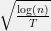 . In other words, I can have an average score within
. In other words, I can have an average score within  of the best advisor after
of the best advisor after  rounds of betting.
rounds of betting.
One reason that this is remarkable is that it does not depend at all on how the data are distributed; the data could be i.i.d., positively correlated, negatively correlated, even adversarial, and one can still construct an (adaptive) prediction rule that does almost as well as the best predictor in the family.
To be even more concrete, if we assume that all costs and payoffs are bounded by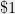 per round, and that there are
per round, and that there are 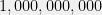 people in total, then an explicit upper bound is that after
people in total, then an explicit upper bound is that after 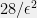 rounds, we will be within
rounds, we will be within  dollars on average of the best other person. Under slightly stronger assumptions, we can do even better, for instance if the best person has an average variance of
dollars on average of the best other person. Under slightly stronger assumptions, we can do even better, for instance if the best person has an average variance of 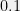 about their mean, then the
about their mean, then the 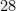 can be replaced with
can be replaced with 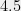 .
.
It is important to note that the betting scenario is just a running example, and one can still obtain regret bounds under fairly general scenarios;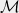 could be continuous and
could be continuous and 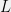 could have quite general structure; the only technical assumption is that
could have quite general structure; the only technical assumption is that 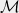 be a convex set and that
be a convex set and that 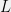 be a convex function of
be a convex function of  . These assumptions tend to be easy to satisfy, though I have run into a few situations where they end up being problematic, mainly for computational reasons. For an
. These assumptions tend to be easy to satisfy, though I have run into a few situations where they end up being problematic, mainly for computational reasons. For an 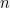 -dimensional model family, typically
-dimensional model family, typically 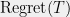 decreases at a rate of
decreases at a rate of  , although under additional assumptions this can be reduced to
, although under additional assumptions this can be reduced to 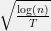 , as in the betting example above. I would consider this reduction to be one of the crowning results of modern frequentist statistics.
, as in the betting example above. I would consider this reduction to be one of the crowning results of modern frequentist statistics.
Yes, these guarantees sound incredibly awesome and perhaps too good to be true. They actually are that awesome, and they are actually true. The work is being done by measuring the error relative to the best model in the model family. We aren’t required to do well in an absolute sense, we just need to not do any worse than the best model. Of as long as at least one of the models in our family makes good predictions, that means we will as well. This is really what statistics is meant to be doing: you come up with everything you imagine could possibly be reasonable, and hand it to me, and then I come up with an algorithm that will figure out which of the things you handed me was most reasonable, and will do almost as well as that. As long as at least one of the things you come up with is good, then my algorithm will do well. Importantly, due to the dependence on the dimension of the model family, you can actually write down extremely broad classes of models and I will still successfully sift through them.
dependence on the dimension of the model family, you can actually write down extremely broad classes of models and I will still successfully sift through them.
Let me stress again: regret bounds are saying that, no matter how the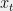 and
and 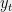 are related, no i.i.d. assumptions anywhere in sight, we will do almost as well as any predictor
are related, no i.i.d. assumptions anywhere in sight, we will do almost as well as any predictor 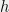 in
in 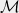 (in particular, almost as well as the best predictor).
(in particular, almost as well as the best predictor).
Myth 6: frequentist methods can only deal with simple models and need to make arbitrary cutoffs in model complexity. A naive perusal of the literature might lead one to believe that frequentists only ever consider very simple models, because many discussions center on linear and log-linear models. To dispel this, I will first note that there are just as many discussions that focus on much more general properties such as convexity and smoothness, and that can achieve comparably good bounds in many cases. But more importantly, the reason we focus so much on linear models is because we have already reduced a large family of problems to (log-)linear regression. The key insight, and I think one of the most important insights in all of applied mathematics, is that of featurization: given a non-linear problem, we can often embed it into a higher-dimensional linear problem, via a feature map (
(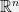 denotes
denotes 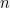 -dimensional space, i.e. vectors of real numbers of length
-dimensional space, i.e. vectors of real numbers of length 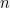 ). For instance, if I think that
). For instance, if I think that 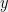 is a polynomial (say cubic) function of
is a polynomial (say cubic) function of  , I can apply the mapping
, I can apply the mapping  , and now look for a linear relationship between
, and now look for a linear relationship between 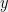 and
and  .
.
This insight extends far beyond polynomials. In combinatorial domains such as natural language, it is common to use indicator features: features that are if a certain event occurs and
if a certain event occurs and 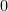 otherwise. For instance, I might have an indicator feature for whether two words appear consecutively in a sentence, whether two parts of speech are adjacent in a syntax tree, or for what part of speech a word has. Almost all state of the art systems in natural language processing work by solving a relatively simple regression task (typically either log-linear or max-margin) over a rich feature space (often involving hundreds of thousands or millions of features, i.e. an embedding into
otherwise. For instance, I might have an indicator feature for whether two words appear consecutively in a sentence, whether two parts of speech are adjacent in a syntax tree, or for what part of speech a word has. Almost all state of the art systems in natural language processing work by solving a relatively simple regression task (typically either log-linear or max-margin) over a rich feature space (often involving hundreds of thousands or millions of features, i.e. an embedding into  or
or 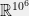 ).
).
A counter-argument to the previous point could be: “Sure, you could create a high-dimensional family of models, but it’s still a parameterized family. I don’t want to be stuck with a parameterized family, I want my family to include all Turing machines!” Putting aside for a second the question of whether “all Turing machines” is a well-advised model choice, this is something that a frequentist approach can handle just fine, using a tool called regularization, which after featurization is the second most important idea in statistics.
Specifically, given any sufficiently quickly growing function , one can show that, given
, one can show that, given 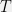 data points, there is a strategy whose average error is at most
data points, there is a strategy whose average error is at most  worse than any estimator
worse than any estimator 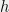 . This can hold even if the model class
. This can hold even if the model class 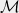 is infinite dimensional. For instance, if
is infinite dimensional. For instance, if 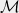 consists of all probability distributions over Turing machines, and we let
consists of all probability distributions over Turing machines, and we let 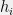 denote the probability mass placed on the
denote the probability mass placed on the 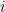 th Turing machine, then a valid regularizer
th Turing machine, then a valid regularizer  would be
would be
If we consider this, then we see that, for any probability distribution over the first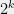 Turing machines (i.e. all Turing machines with description length
Turing machines (i.e. all Turing machines with description length 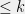 ), the value of
), the value of  is at most
is at most  . (Here we use the fact that
. (Here we use the fact that  , since
, since 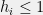 and hence
and hence 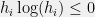 .) This means that, if we receive roughly
.) This means that, if we receive roughly 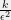 data, we will achieve error within
data, we will achieve error within  of the best Turing machine that has description length
of the best Turing machine that has description length 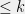 .
.
Let me note several things here:
Interestingly, in the case that the prediction error is given by the negative log probability assigned to the truth, then the corresponding strategy that achieves the error bound is just normal Bayesian updating. But for other measurements of error, we get different update strategies. Although I haven’t worked out the math, intuitively this difference could be important if the universe is fundamentally unpredictable but our notion of error is insensitive to the unpredictable aspects.
Myth 7: frequentist methods hide their assumptions while Bayesian methods make assumptions explicit. I’m still not really sure where this came from. As we’ve seen numerous times so far, a very common flavor among frequentist methods is the following: I have a model class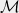 , I want to do as well as any model in
, I want to do as well as any model in 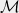 ; or put another way:
; or put another way:
Assumption: At least one model in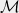 has error at most
has error at most 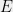 .
.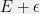 .
.
Guarantee: My method will have error at most
This seems like a very explicit assumption with a very explicit guarantee. On the other hand, an argument I hear is that Bayesian methods make their assumptions explicit because they have an explicit prior. If I were to write this as an assumption and guarantee, I would write:
Assumption: The data were generated from the prior.
Guarantee: I will perform at least as well as any other method.
While I agree that this is an assumption and guarantee of Bayesian methods, there are two problems that I have with drawing the conclusion that “Bayesian methods make their assumptions explicit”. The first is that it can often be very difficult to understand how a prior behaves; so while we could say “The data were generated from the prior” is an explicit assumption, it may be unclear what exactly that assumption entails. However, a bigger issue is that “The data were generated from the prior” is an assumption that very rarely holds; indeed, in many cases the underlying process is deterministic (if you’re a subjective Bayesian then this isn’t necessarily a problem, but it does certainly mean that the assumption given above doesn’t hold). So given that that assumption doesn’t hold but Bayesian methods still often perform well in practice, I would say that Bayesian methods are making some other sort of “assumption” that is far less explicit (indeed, I would be very interested in understanding what this other, more nebulous assumption might be).
Myth 8: frequentist methods are fragile, Bayesian methods are robust. This is another one that’s straightforwardly false. First, since frequentist methods often rest on weaker assumptions they are more robust if the assumptions don’t quite hold. Secondly, there is an entire area of robust statistics, which focuses on being robust to adversarial errors in the problem data.
Myth 9: frequentist methods are responsible for bad science. I will concede that much bad science is done using frequentist statistics. But this is true only because pretty much all science is done using frequentist statistics. I’ve heard arguments that using Bayesian methods instead of frequentist methods would fix at least some of the problems with science. I don’t think this is particularly likely, as I think many of the problems come from mis-application of statistical tools or from failure to control for multiple hypotheses. If anything, Bayesian methods would exacerbate the former, because they often require more detailed modeling (although in most simple cases the difference doesn’t matter at all). I don’t think being Bayesian guards against multiple hypothesis testing. Yes, in some sense a prior “controls for multiple hypotheses”, but in general the issue is that the “multiple hypotheses” are never written down in the first place, or are written down and then discarded. One could argue that being in the habit of writing down a prior might make practitioners more likely to think about multiple hypotheses, but I’m not sure this is the first-order thing to worry about.
Myth 10: frequentist methods are unprincipled / hacky. One of the most beautiful theoretical paradigms that I can think of is what I could call the “geometric view of statistics”. One place that does a particularly good job of show-casing this is Shai Shalev-Shwartz’s PhD thesis, which was so beautiful that I cried when I read it. I’ll try (probably futilely) to convey a tiny amount of the intuition and beauty of this paradigm in the next few paragraphs, although focusing on minimax estimation, rather than online learning as in Shai’s thesis.
The geometric paradigm tends to emphasize a view of measurements (i.e. empirical expected values over observed data) as “noisy” linear constraints on a model family. We can control the noise by either taking few enough measurements that the total error from the noise is small (classical statistics), or by broadening the linear constraints to convex constraints (robust statistics), or by controlling the Lagrange multipliers on the constraints (regularization). One particularly beautiful result in this vein is the duality between maximum entropy and maximum likelihood. (I can already predict the Jaynesians trying to claim this result for their camp, but (i) Jaynes did not invent maximum entropy; (ii) maximum entropy is not particularly Bayesian (in the sense that frequentists use it as well); and (iii) the view on maximum entropy that I’m about to provide is different from the view given in Jaynes or by physicists in general [edit: EHeller thinks this last claim is questionable, see discussion here].)
To understand the duality mentioned above, suppose that we have a probability distribution and the only information we have about it is the expected value of a certain number of functions, i.e. the information that
and the only information we have about it is the expected value of a certain number of functions, i.e. the information that ![{\mathbb{E}[\phi(x)] = \phi^*} {\mathbb{E}[\phi(x)] = \phi^*}](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BE%7D%5B%5Cphi%28x%29%5D+%3D+%5Cphi%5E%2A%7D&bg=f0f0f0&fg=000000&s=0) , where the expectation is taken with respect to
, where the expectation is taken with respect to  . We are interested in constructing a probability distribution
. We are interested in constructing a probability distribution 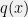 such that no matter what particular value
such that no matter what particular value  takes,
takes, 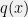 will still make good predictions. In other words (taking
will still make good predictions. In other words (taking 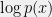 as our measurement of prediction accuracy) we want
as our measurement of prediction accuracy) we want ![{\mathbb{E}_{p'}[\log q(x)]} {\mathbb{E}_{p'}[\log q(x)]}](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BE%7D_%7Bp%27%7D%5B%5Clog+q%28x%29%5D%7D&bg=f0f0f0&fg=000000&s=0) to be large for all distributions
to be large for all distributions 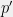 such that
such that ![{\mathbb{E}_{p'}[\phi(x)] = \phi^*} {\mathbb{E}_{p'}[\phi(x)] = \phi^*}](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BE%7D_%7Bp%27%7D%5B%5Cphi%28x%29%5D+%3D+%5Cphi%5E%2A%7D&bg=f0f0f0&fg=000000&s=0) . Using a technique called Lagrangian duality, we can both find the optimal distribution
. Using a technique called Lagrangian duality, we can both find the optimal distribution 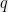 and compute its worse-case accuracy over all
and compute its worse-case accuracy over all 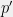 with
with ![{\mathbb{E}_{p'}[\phi(x)] = \phi^*} {\mathbb{E}_{p'}[\phi(x)] = \phi^*}](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BE%7D_%7Bp%27%7D%5B%5Cphi%28x%29%5D+%3D+%5Cphi%5E%2A%7D&bg=f0f0f0&fg=000000&s=0) . The characterization is as follows: consider all probability distributions
. The characterization is as follows: consider all probability distributions 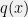 that are proportional to
that are proportional to  for some vector
for some vector 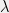 , i.e.
, i.e. 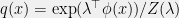 for some
for some 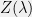 . Of all of these, take the q(x) with the largest value of
. Of all of these, take the q(x) with the largest value of  . Then
. Then 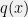 will be the optimal distribution and the accuracy for all distributions
will be the optimal distribution and the accuracy for all distributions 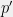 will be exactly
will be exactly  . Furthermore, if
. Furthermore, if 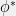 is the empirical expectation given some number of samples, then one can show that
is the empirical expectation given some number of samples, then one can show that  is propotional to the log likelihood of
is propotional to the log likelihood of 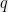 , which is why I say that maximum entropy and maximum likelihood are dual to each other.
, which is why I say that maximum entropy and maximum likelihood are dual to each other.
This is a relatively simple result but it underlies a decent chunk of models used in practice.
Myth 11: frequentist methods have no promising approach to computationally bounded inference. I would personally argue that frequentist methods are more promising than Bayesian methods at handling computational constraints, although computationally bounded inference is a very cutting edge area and I’m sure other experts would disagree. However, one point in favor of the frequentist approach here is that we already have some frameworks, such as the “tightening relaxations” framework discussed here, that provide quite elegant and rigorous ways of handling computationally intractable models.
References
(Myth 3) Sparse recovery: Sparse recovery using sparse matrices
(Myth 5) Online learning: Online learning and online convex optimization
(Myth 8) Robust statistics: see this blog post and the two linked papers
(Myth 10) Maximum entropy duality: Game theory, maximum entropy, minimum discrepancy and robust Bayesian decision theory