Uncharitable Summary
Most likely there’s something in the intuitions which got lost when transmitted to me via reading this text, but the mathematics itself seems pretty tautological to me (nevertheless I found it interesting since tautologies can have interesting structure! The proof itself was not trivial to me!).
Here is my uncharitable summary:
Assume you have a Markov chain M_0 → M_1 → M_2 → … → M_n → … of variables in the universe. Assume you know M_n and want to predict M_0. The Telephone theorem says two things:
- You don’t need to keep all information about M_n to predict M_0 as well as possible. It’s enough to keep the conditional distribution P(M_0 | M_n).
- Additionally, in the long run, these conditional distributions grow closer and closer together: P(M_0 | M_n) ~ P(M_0 | M_{n+1})
That’s it. The first statement is tautological, and the second states that you cannot keep losing information. At some point, your uncertainty in M_0 stabilizes.
Further Thoughts
- I think actually, John wants to claim that the conditional probabilities can be replaced by something else which carries information at a distance and stabilizes over time. Something like:
- Average measurements
- Pressure/temperature of a gas
- Volume of a box
- Length of a message
- …
- These things could then serve as “sufficient statistics” that contain everything one needs for making predictions. I have no idea of how one would go about finding such conserved quantities in general systems. John also makes a related remark:
- “(Side note: the previous work already suggested conditional probability distributions as the type-signature of abstractions, but that’s quite general, and therefore not very efficient to work with algorithmically. Estimates-of-deterministic-constraints are a much narrower subset of conditional probability distributions.)”
- The math was made easier in the proof by assuming that information at a distance precisely stabilizes at some point. In reality, it may slowly converge without becoming constant. For this, no proof or precise formulation is yet in the text.
John claims: “I believe that most abstractions used by humans in practice are summaries of information relevant at a distance. The theorems in this post show that those summaries are estimates/distributions of deterministic (in the limit) constraints in the systems around us.”This confuses me. It seems like this claims that we can also use summaries of very closeby objects to make predictions at arbitrary distance. However, the mathematics doesn’t show this: it only considers varying the “sender” of information,notvarying the “receiver” (which in the case of the theorem is M_0!). If you want to make predictionsaboutarbitrarily far away different things in the universe, then it's unclear whether you can throw any information of closeby things away. (But maybe I misunderstood the text here?)
A somewhat more random comment:
I disagree with the claim that the intuitions behind information diagrams fall apart at higher degrees: if you’re “just fine” with negative information, then you can intersect arbitrarily many circles and get additivity rules for information terms. I actually wrote a paper about this, including how one can do this for other information quantities like Kolmogorov complexity and Kullback-Leibler divergence. What’s problematic about this is not the mathematics of intersecting circles, but that we largely don’t have good real-world interpretations and use cases for it.
This is a great theorem that's stuck around in my head this last year! It's presented clearly and engagingly, but more importantly, the ideas in this piece are suggestive of a broader agent foundations research direction. If you wanted to intimate that research direction with a single short post that additionally demonstrates something theoretically interesting in its own right, this might be the post you'd share.
I'm trying to understand how to map between the definition of Markov blanket used in this post (a partition of the variables in two such that the variables in one set are independent of the variables in the other given the variables on edges which cross the partition) and the one I'm used to (a Markov blanket of a set of variables is another set of variables such that the first set is independent of everything else given the second). I'd be grateful if anyone can tell me whether I've understood it correctly.
There are three obstacles to my understanding: (i) I'm not sure what 'variables on edges' means, and John also uses the phrase 'given the values of the edges' which confuses me, (ii) the usual definition is with respect to some set of variables, but the one in this post isn't, (iii) when I convert between the definitions, the place I have to draw the line on the graph changes, which makes me suspicious.
Here's me attempting to overcome the obstacles:
(i) I'm assuming 'variables on the edges' means the parents of the edges, not the children or both. I'm assuming 'values of edges' means the values of the parents.
(ii) I think we can reconcile this by saying that if M is a Markov blanket of a set of variables V in the usual sense, then a line which cuts through an outgoing edge of each variable in M is a Markov blanket in the sense of this post. Conversely, if some Markov blanket in the sense of this post parititons our graph into A and B, then the set M of parents of edges crossing the partion forms a Markov blanket of both A\M and B\M in usual sense.
(iii) I think I have to suck it up and accept that the lines look different. In this picture, the nodes in the blue region (except A) form a Markov blanket for A in the usual sense. The red line is a Markov blanket in the sense of this post.
Does this seem right?
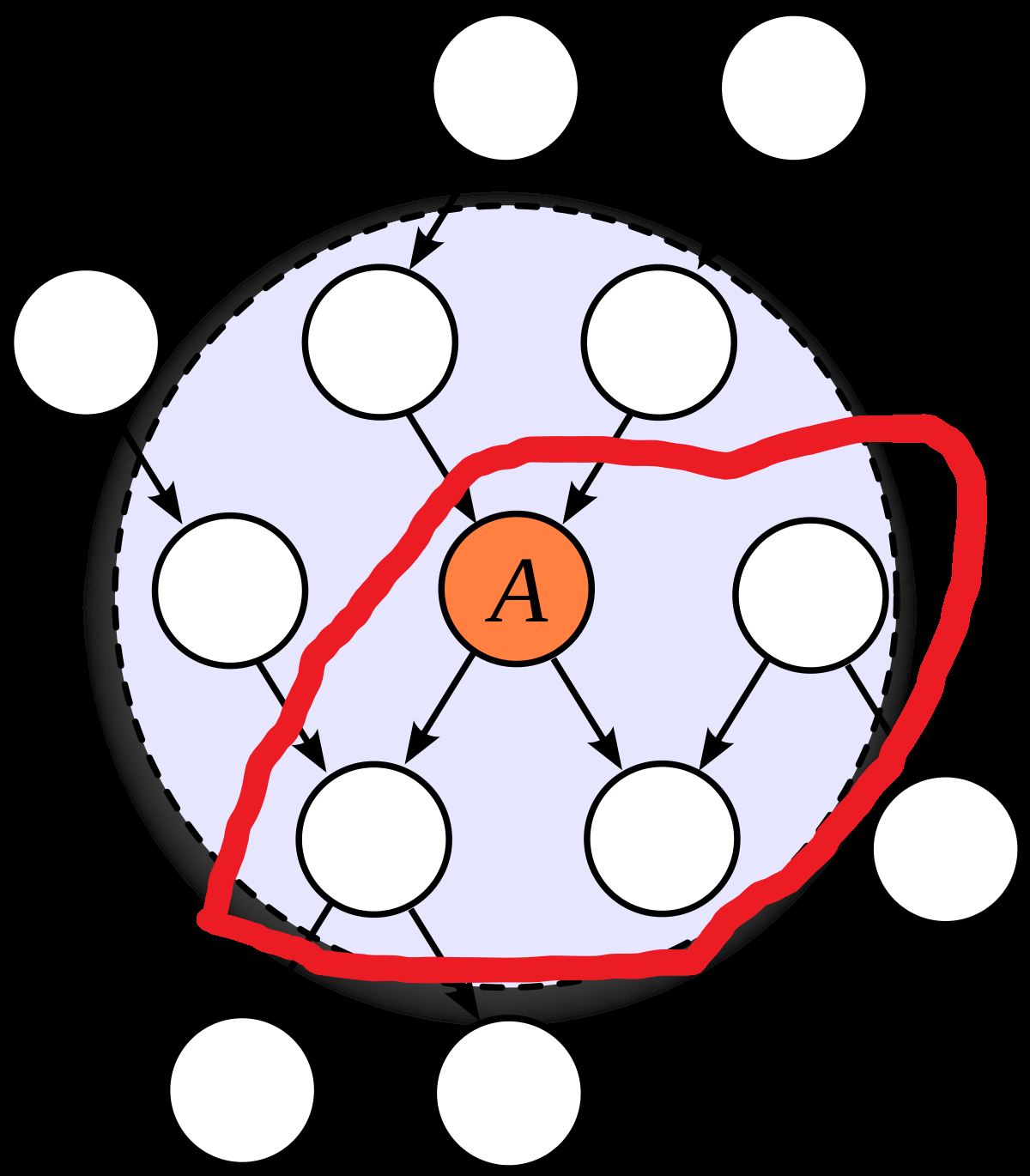
That's basically right in terms of the math, but I'll walk through the intuitive story a bit more.
First, "edge values" or "variables on edges". When we think of a DAG model in message-passing terms, each edge carries a message from parent to child. The content of that message is the value of the parent variable. That's the "edge value" or "edge variable" which gets included in the Markov blanket.
Now, if we find a cut through the graph (i.e. a set of edges which we could remove to split the graph into two disconnected pieces), then the edges in that cut carry all the messages between the two pieces. No communication between the two pieces occurs, except via the messages carried by those edges. So, intuitively, we'd expect the two pieces to be independent conditional on the messages passed over the edges in the cut. That's the intuitive story behind a Markov blanket.
The usual definition of a Markov blanket is equivalent, but formulating it in terms of vertices rather than edges is more awkward. For instance, when we talk about the Markov blanket of one variable, we usually say that the blanket consists of the variable's parents, children and spouses. What an awkward definition! What's up with the spouses? With the edges picture, it's clear what's going on: we're drawing a blanket around the variable and its children. The edges which pass through that blanket carry values of parents, children and spouses.
I'm sure you already know this, but information can also travel a large distance in one hop, like when I look up at night and see a star. Or if someone 100 years ago took a picture of a star, and I look at the picture now, information has traveled 110 years and 10 light-years in just two hops.
But anyway, your discussion seems reasonable AFAICT for the case you're thinking of.
We can still view these as travelling through many layers - the light waves have to propagate through many lightyears of mostly-empty space (and it could attenuate or hit things along the way). The photo has to last many years (and could randomly degrade a little or be destroyed at any moment along the way).
What makes it feel like "one hop" intuitively is that the information is basically-perfectly conserved at each "step" through spacetime, and there's in a symmetry in how the information is represented.
The basic idea seem to me interesting and true, but I think some important ingredients are missing, or more likely missing in my understanding of what you say:
-
It seem like you upper-bound the abstractions we may use by basically the information that we may access (actually even higher, assuming you do not exclude what the neighbour does behind closed doors). But isn't this bound very loose? I mean, it seem like every pixel of my sight count as "information at a distance", and my world model is much much smaller.
-
is time treated the like space? From the one hand it seem like it have to if we want to abstract colour from sequence of amplitudes, but it also feels meaningfully different.
-
is the punch to define objects as blankets with much more information inside than may be viewed from far outside?
-
the part where all the information that may be lost in the next layer is assumed to already been lost, seen to assume symmetries - are those explicit part of the project?
-
in practice, there seem to be information loss and practically-indeterminism in all scales. E.g. when i go further from a picture i keep losing details. Wouldn't it make more sense to talk about how far (in orders of magnitude) information travel rather than saying that n either does it does not go to infinity?
Sorry about my English, hope it was clear enough
I love the idea behind this post, and I've come back to it many times over the years. Now I’m coming back to it with error correction on my mind.
I agree that in a game of telephone only information which is preserved through each step will make it to the end. But many processes are unlike this. E.g., normally if you didn’t hear something I said, you can ask. And one could imagine arbitrarily long gaps—you ask me to clarify in a week or a month or what have you. Or maybe someone has an insight and then loses it, gains it again, and then writes a book such that the information is pretty reliably transmitted in the world.
In all such cases there will be a few to many layers of the nested Markov structure which lose the information but gain it again at a later point. Which is to say that the constraint of needing each intermediate state to carry the information in order for the information to be preserved seems too strong. “Ability to recover the information” seems like a necessary constraint, although not sufficient: you need some kind of error corrector or the original generative process to run again in order to in fact recover it.
When you write I understand that to mean that for all . But when I look up definitions of conditional probability it seems that that notation would usually mean for all
Am I confused or are you just using non-standard notation?
Your interpretation of my notation is correct. The notation is not uncommon, but it does diverge from the notation used for conditional probability in other contexts. (More generally, notation for probability is an absolute mess in practice, with context determining a lot.)
Can you explain how the generalized KPD fits into all of this? KPD is about estimating the parameters of a model from samples via a low dimensional statistic, whereas you are talking about estimating one part of a sample from another (distant) part of the sample via a low dimensional statistic. Are you using KPD to rule out "high-dimensional" correlations going through the parameters of the model?
Roughly speaking, the generalized KPD says that if the long-range correlations are low dimensional, then the whole distribution is exponential family (modulo a few "exceptional" variables). The theorem doesn't rule out the possibility of high-dimensional correlations, but it narrows down the possible forms a lot if we can rule out high-dimensional correlations some other way. That's what I'm hoping for: some simple/common conditions which limit the dimension of the long-range correlations, so that gKPD can apply.
This post says that those long range correlations have to be mediated by deterministic constraints, so if the dimension of the deterministic constraints is low, then that's one potential route. Another potential route is some kind of information network flow approach - i.e. if lots of information is conserved along one "direction", then that should limit information flow along "orthogonal directions", which would mean that long-range correlations are limited between "most" local chunks of the graph.
I'm still confused. What direction of GKPD do you want to use? It sounds like you want to use the low-dimensional statistic => exponential family direction. Why? What is good about some family being exponential?
Yup, that's the direction I want. If the distributions are exponential family, then that dramatically narrows down the space of distributions which need to be represented in order to represent abstractions in general. That means much simpler data structures - e.g. feature functions and Lagrange multipliers, rather than whole distributions.
So, your thesis is, only exponential models give rise to nice abstractions? And, since it's important to have abstractions, we might just as well have our agents reason exclusively in terms of exponential models?
More like: exponential family distributions are a universal property of information-at-a-distance in large complex systems. So, we can use exponential models without any loss of generality when working with information-at-a-distance in large complex systems.
That's what I hope to show, anyway.
As I understand it, the proof in the appendix only assumes we're working with Bayes nets (so just factorizations of probability distributions). That is, no assumption is made that the graphs are causal in nature (they're not necessarily assumed to be the causal diagrams of SCMs) although of course the arguments still port over if we make that stronger assumption.
Is that correct?
This ML paper seems potentially relevant; it trains a neural network to find features where you can improve your predictions of information at a time distance by assuming the features to be better conserved.
Nice! That is a pretty good fit for the sorts of things the Telephone Theorem predicts, and potentially relevant information for selection theorems as well.
Is every line you can draw through the causal model a Markov blanket?
It seems like you're interested in Markov blankets because the information on one side is independent from the other side given the values of the edges that pass through. But it also looks like the edges in the original graph represent "has any effect on". Which makes it sound like you're saying one side is independent from the other except for all of the ways in which it's not, which seems trivial. What am I missing?
You're basically correct. The substantive part is that, if I say " is a Markov blanket separating from ", then I'm claiming that is a comprehensive list of all the "ways in which and are not independent". If we have a Markov blanket, then we know exactly "which channels" the two sides can interact through; we can rule out any other interactions.
Kinda sounds like the important part is not the blankets themselves, but the relationships between them? That is, a Markov blanket is just any partition of the graph, but it's important that you can assert that is "separating" and . (Whereas if you just took 3 random partitions, none of them would necessarily separate the other 2.)
Or is it more like--we don't actually have any explicit representation of the entire causal model, so we can't necessarily use a partition to calculate all the edges that cross that partition, and the Markov blanket is like a list of the edges, rather than a list of the nodes? Every partition describes a Markov blanket, but not every set of edges does, so saying that this particular set of edges forms a Markov blanket is a non-trivial statement about those edges?
These are both correct. The first is right in most applications of Markov blankets. The second is relevant mainly in e.g. science, where figuring out the causal structure is part of the problem. In science, we can experimentally test whether mediates the interaction between and (i.e. whether is a Markov blanket between and ), and then we can back out information about the causal structure from that.
This has a curious relationship to some math ideas like the golden ratio. Take a rectangle proportioned in the golden ratio. If you take away a square with side length equal to the smaller side length of the rectangle, the remaining smaller rectangle is equal to the golden ratio. Information is propagated perfectly.
Imagine that we were given a rectangle, and told that it was produced by modifying a previous rectangle via this procedure (by "small-side chopping"). We couldn't recover the original precisely unless it was in the golden ratio. But if it is in the golden ratio, we can recover it. Intuitively, it seems like we could recover an approximation, depending on how close the rectangle we're given is to the original. We can certainly recover one of the side lengths.
Edit: You actuall can reconstruct the previous rectangle in the sequence. If a rectangle has side lengths a and b, then small-side chopping produces a rectangle of side lengths [a, b - a]. We still have access to perfect information about the previous side lengths.
It also seems possible that if you start with a randomly proportioned rectangle, then performing this procedure will cause it to converge on a rectangle in the golden ratio. Again, I'm not sure. If so, will it actually reach a golden rectangle? Or just approach it in the limit?
Edit: Given that we preserve perfect information about the previous rectangle after performing small-side chopping, this procedure cannot ultimately generate a golden rectangle.
If these intuitions are correct, then a golden rectangle is a concrete example of what the endpoint of information loss can look like. Often, we visualize loss of information as a void, or as random noise. It can also just be a static pattern. This is odd, since static patterns look like "information." But what is information?
You know the game of Telephone? That one where a bunch of people line up, and the first person whispers some message in the second person’s ear, then the second person whispers it to the third, and so on down the line, and then at the end some ridiculous message comes out from all the errors which have compounded along the way.
This post is about modelling the whole world as a game of Telephone.
Information Not Perfectly Conserved Is Completely Lost
Information is not binary; it’s not something we either know or don’t. Information is uncertain, and that uncertainty lies on a continuum - 10% confidence is very different from 50% confidence which is very different from 99.9% confidence.
In Telephone, somebody whispers a word, and I’m not sure if it’s “dish” or “fish”. I’m uncertain, but not maximally uncertain; I’m still pretty sure it’s one of those two words, and I might even think it’s more likely one than the other. Information is lost, but it’s not completely lost.
But if you’ve played Telephone, you probably noticed that by the time the message reaches the end, information is more-or-less completely lost, unless basically-everyone managed to pass the message basically-perfectly. You might still be able to guess the length of the original message (since the length is passed on reasonably reliably), but the contents tend to be completely scrambled.
Main takeaway: when information is passed through many layers, one after another, any information not nearly-perfectly conserved through nearly-all the “messages” is lost. Unlike the single-message case, this sort of “long-range” information passing is roughly binary.
In fact, we can prove this mathematically. Here’s the rough argument:
This does allow a little bit of wiggle room - non-binary uncertainty can enter the picture early on. But in the long run, any information not nearly-perfectly conserved by the later steps will be lost.
Of course, the limit which the mutual information approaches could still be zero - meaning that all the information is lost. Any information not completely lost must be perfectly conserved in the long run.
Deterministic Constraints
It turns out that information can only be perfectly conserved when carried by deterministic constraints. For instance, in Telephone, information about the length of the original message will only be perfectly conserved if the length of each message is always (i.e. deterministically) equal to the length of the preceding message. There must be a deterministic constraint between the lengths of adjacent messages, and our perfectly-conserved information must be carried by that constraint.
More formally: suppose our game of telephone starts with the message M0. Some time later, the message Mn is whispered into my ear, and I turn around to whisper Mn+1 into the next person’s ear. The only way that Mn+1 can contain exactly the same information as Mn about M0 is if:
Proof is in the Appendix.
Upshot of this: we can characterize information-at-a-distance in terms of the deterministic constraints in a system. The connection between Mn and Mn+1 is an information “channel”; only the information encoded in deterministic constraints between Mn and Mn+1 will be perfectly conserved. Since any information not perfectly conserved is lost, only those deterministic constraints can carry information “at a distance”, i.e. in the large-n limit.
The Thing For Which Telephone Is A Metaphor
Imagine we have a toaster, and we’re trying to measure its temperature from the temperature of the air some distance away. We can think of the temperature of the toaster itself as the “original message” in a game of Telephone. The “message” is passed along by many layers of air molecules in between our toaster and our measurement device.
(Note: unlike the usual game of Telephone, the air molecules could also be “encoding” the information in nontrivial ways, rather than just passing it along with some noise mixed in. For instance, the air molecules may be systematically cooler than the toaster. That’s not noise; it’s a predictable difference which we can adjust for. In other words, we can “decode” the originally-hotter temperature which has been “encoded” as a systematically-cooler temperature by the molecules. On the other hand, there will also be some unpredictable noise from e.g. small air currents.)
More generally, whenever information is passed “over a long distance” (or a long time) in a physical system, there’s many layers of “messages” in between the start and the end. (This has to be the case, because the physics of our universe is local.) So, we can view it as a game of telephone: the only information which is passed over a sufficiently-long “distance” is information perfectly transmitted by deterministic constraints in the system. Everything else is lost.
Let’s formalize this.
Suppose we have a giant causal model representing the low-level physics of our universe:
We can draw cuts in this graph, i.e. lines which “cut off” part of the graph from the rest. In the context of causal models, these are called “Markov blankets”; their interpretation is that all variables on one side are statistically independent of all variables on the other side given the values of any edges which cross the blanket. For instance, a physical box which I close at one time and open at a later time is a Markov blanket - the inside can only interact with the outside via the walls of the box or via the state when the box is first closed/opened (i.e. the “walls” along the time-dimension).
We want to imagine a sequence of nested Markov blankets, each cutting off all the previous blankets from the rest of the graph. These Markov blankets are the “messages” in our metaphorical game of Telephone. In the toaster example, these are sequential layers of air molecules between the toaster and the measurement.
Our theorem says that, in the “long distance” limit (i.e. n→∞), constraints of the form fn(Mn)=fn+1(Mn+1) determine which information is transmitted. Any information not perfectly carried by the deterministic constraints is lost.
Another example: consider a box of gas, just sitting around. We can choose our “layers of nested Markov blankets” to be snapshots of the microscopic states of all the molecules at sequential times. At the microscopic level, molecules are bouncing around chaotically; quantum uncertainty is quickly amplified by the chaos. The only information which is relevant to long-term predictions about the gas molecules is information carried by deterministic constraints - e.g. conservation of energy, conservation of the number of molecules, or conservation of the volume of the box. Any other information about the molecules’ states is eventually lost. So, it’s natural to abstractly represent the “gas” via the “macroscopic state variables” energy, molecule count and volume (or temperature, density and pressure, which are equivalent); these are the variables which can carry information over long time horizons. If we found some other deterministic constraint on the molecules’ dynamics, we might want to add that to our list of state variables.
The Big Loophole
Note that our constraints only need to be deterministic in the limit. At any given layer, they need only be “approximately deterministic”, i.e. fn(Mn)=fn+1(Mn+1) with probability close to 1 (or fn(Mn)≈fn+1(Mn+1), in which case the leading-order bits are equal with probability close to 1). As long as that approximation improves at each step, converging to perfect determinism in the limit, it works.
In practice, this is mainly relevant when information is copied redundantly over many channels.
An example: suppose I start with a piece of string, cut two more pieces of string to match its length, then throw out the original. Each of the two new strings has some “noise” in its length, which we’ll pretend is normal with mean zero and standard deviation σ, independent across the two strings.
Now, I iterate the process. For each of my two pieces of string, I cut two new pieces to match the length of that one, and throw away my old string. Again, noise is added in the process; same assumptions as before. Then, for each of my four pieces of string, I cut two new pieces to match the length of that one, and throw away my old string. And so forth.
We can represent this as a binary-tree-shaped causal model; each new string is an independent noisy measurement of its parent:
… and we can draw layers of Markov blankets horizontally:
Now, there is never any deterministic constraint between Mn and Mn+1; Mn+1 is just a bunch of “measurements” of Mn, and every one of those measurements has some independent noise in it.
And yet, it turns out that information is transmitted in the limit in this system. Specifically, the 2n measurements at layer n are equivalent to a single noisy measurement of the original string length with normally-distributed noise of magnitude √2n−12nσ. In the limit, it converges to a single measurement with noise of standard deviation σ. That’s not a complete loss of information.
So what’s the deterministic constraint which carries that information? We can work backward through the proofs to calculate it; it turns out to be the average of the measurements at each layer. Because the noise in each measurement is independent (given the previous layer), the noise in the average shrinks at each step. In the limit, the average of one layer becomes arbitrarily close to the average of the next.
That raises an interesting question: do all deterministic-in-the-limit constraints work roughly this way, in all systems? That is, do deterministic constraints which show up only in the limit always involve an average of conditionally-independent noise terms, i.e. something central-limit-theorem-like? I don’t know yet, but I suspect the answer is “yes”.
Why Is This Interesting?
First, this is a ridiculously powerful mathematical tool. We can take a causal system, choose any nested sequence of Markov blankets which we please, look at deterministic constraints between sequential layers, and declare that only those constraints can transmit information in the limit.
Personally, I’m mostly interested in this as a way of characterizing abstraction. I believe that most abstractions used by humans in practice are summaries of information relevant at a distance. The theorems in this post show that those summaries are estimates/distributions of deterministic (in the limit) constraints in the systems around us. For my immediate purposes, the range of possible “type-signatures” of abstractions has dramatically narrowed; I now have a much better idea of what sort of data-structures to use for representing abstractions. Also, looking for local deterministic constraints (or approximately-deterministic constraints) in a system is much more tractable algorithmically than directly computing long-range probability distributions in large causal models.
(Side note: the previous work already suggested conditional probability distributions as the type-signature of abstractions, but that’s quite general, and therefore not very efficient to work with algorithmically. Estimates-of-deterministic-constraints are a much narrower subset of conditional probability distributions.)
Connections To Some Other Pieces
Content Warning: More jargon-y; skip this section if you don’t want poorly-explained information on ideas-still-under-development.
In terms of abstraction type-signatures and how to efficiently represent them, the biggest remaining question is how exponential-family distributions and the Generalized Koopman-Pitman-Darmois Theorem fit into the picture. In practice, it seems like estimates of those long-range deterministic constraints tend to fit the exponential-family form, but I still don’t have a really satisfying explanation of when or why that happens. Generalized KPD links it to (conditional) independence, which fits well with the overarching framework, but it’s not yet clear how that plays with deterministic constraints in particular. I expect that there’s some way to connect the deterministic constraints to the “features” in the resulting exponential family distributions, similar to a canonical ensemble in statistical mechanics. If that works, then it would complete the characterization of information-at-a-distance, and yield quite reasonable data structures for representing abstractions.
Meanwhile, the theorems in this post already offer some interesting connections. In particular, this correspondence theorem (which I had originally written off as a dead end) turns out to apply directly. So we actually get a particularly strong form of correspondence for abstractions; there’s a fairly strong sense in which all the natural abstractions in an environment fit into one “global ontology”, and the ontologies of particular agents are all (estimates of) subsets of that ontology (to the extent that the agents rely on natural abstractions).
Also, this whole thing fits very nicely with some weird intuitions humans have about information theory. Basically, humans often intuitively think of information as binary/set-like; many of our intuitions only work in cases where information is either perfect or completely absent. This makes representing information quantities via Venn diagrams intuitive, and phenomena like e.g. negative interaction information counterintuitive. But if our “information” is mostly representing information-at-a-distance and natural abstractions, then this intuition makes sense: that information is generally binary/set-like.
Appendix: Information Conservation
We want to know when random variables M1, M2 and X factor according to both M2→M1→X and M1→M2→X, i.e.
P[M2,M1,X]=P[X|M1]P[M1|M2]P[M2]
… and
P[M2,M1,X]=P[X|M2]P[M2|M1]P[M1]
Intuitively, this says that M1 and M2 contain exactly the same information about X; information is perfectly conserved in passing from one to the other.
(Side note: any distribution which factors according to M2→M1→X also factors according to the reversed chain X→M1→M2. In the main post, we mostly pictured the latter structure, but for this proof we’ll use the former; they are interchangeable. We've also replaced "M0" with "X", to distinguish the "original message" more.)
First, we can equate the two factorizations and cancel P[M1,M2] from both sides to find
P[X|M1]=P[X|M2]
... which must hold for ALL M1,M2,X with P[M1,M2]>0. This makes sense: M1 and M2 contain the same information about X, so the distribution of X given M1 is the same as the distribution of X given M2 - assuming that P[M1,M2]>0.
Next, define fk(Mk):=(x→P[X=x|Mk]), i.e. fk gives the posterior distribution of X given Mk. Our condition P[X|M1]=P[X|M2] for all M1,M2,X with P[M1,M2]>0 can then be written as
f1(M1)=f2(M2)
… for all M1,M2 with P[M1,M2]>0. That’s the deterministic constraint. (Note that f matters only up to isomorphism, so any invertible transformation of f can be used instead, as long as we transform both f1 and f2.)
Furthermore, a lemma of the Minimal Map Theorem says that P[X|(x→P[X=x|Mk])]=P[X|Mk], so we also have P[X|Mk]=P[X|fk(Mk)]. In other words, P[X|Mk] depends only on the value of the deterministic constraint.
This shows that any solutions to the information conservation problem must take the form of a deterministic constraint f1(M1)=f2(M2), with X dependent only on the value of the constraint. We can also easily show the converse: if we have a deterministic constraint, with X dependent only on the value of the constraint, then it solves the information conservation problem. This proof is one line:
P[X|M1=m1]=P[X|f1(M1)=f1(m1)]=P[X|f2(M2)=f2(m2)]=P[X|M2=m2]
… for any m1,m2 which satisfy the constraint f1(m1)=f2(m2).