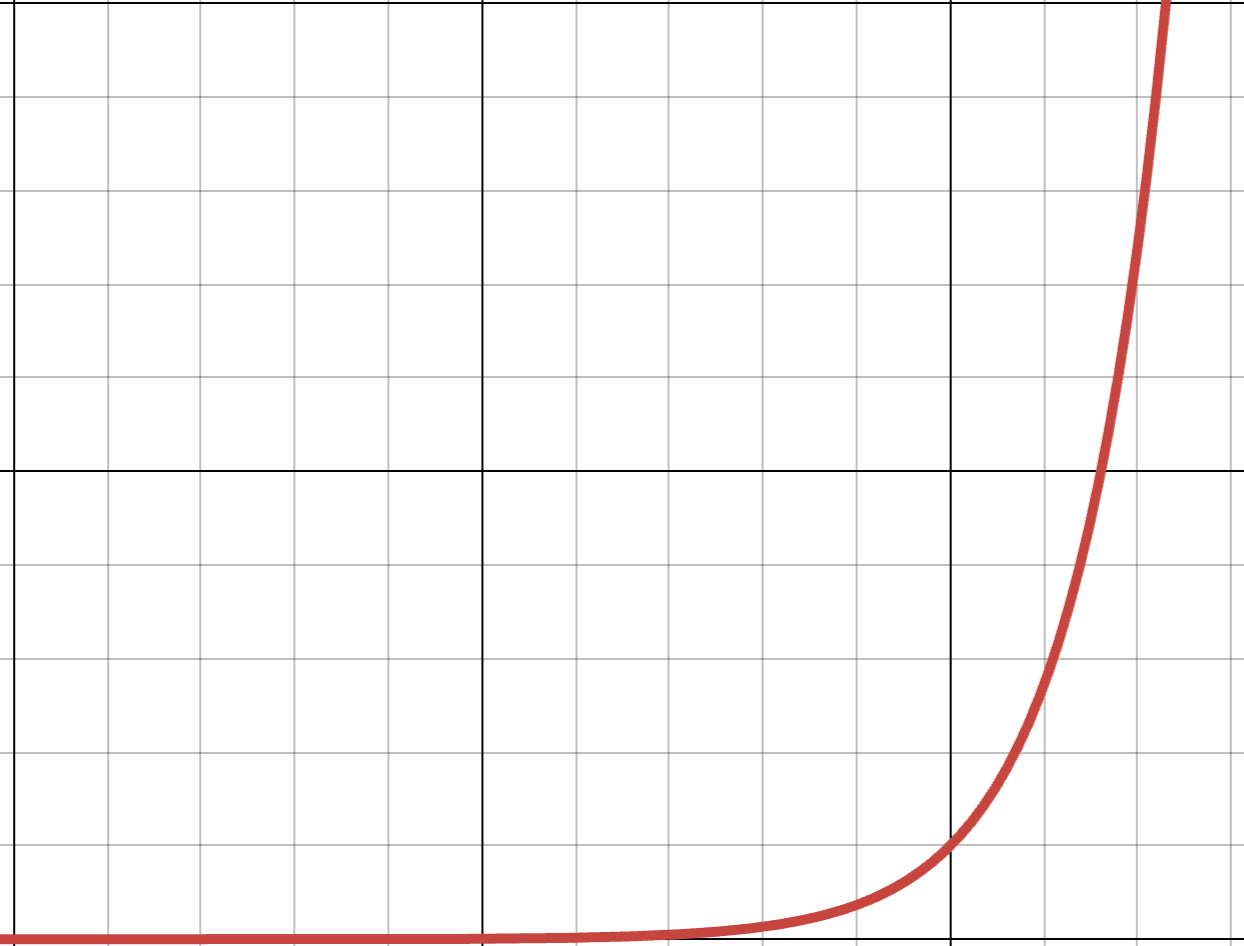
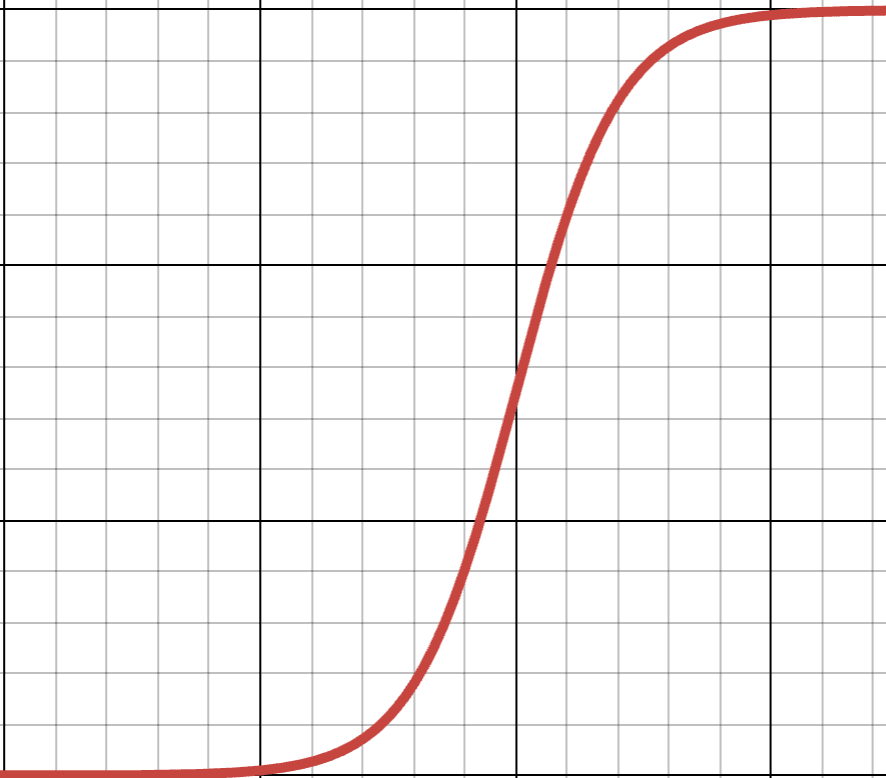
All Exponentials are Eventually S-Curves
25Vladimir_Nesov
6Gordon Seidoh Worley
20AnthonyC
5Gordon Seidoh Worley
2AnthonyC
2Gordon Seidoh Worley
9Cole Wyeth
3Gordon Seidoh Worley
3Cole Wyeth
2Gordon Seidoh Worley
5Cole Wyeth
2Gordon Seidoh Worley
9Veedrac
3Gordon Seidoh Worley
2Veedrac
2Gordon Seidoh Worley
3Veedrac
9Yair Halberstadt
1Gordon Seidoh Worley
9Yair Halberstadt
3Gordon Seidoh Worley
5Yair Halberstadt
2Gordon Seidoh Worley
6Karl Krueger
2Gordon Seidoh Worley
3Karl Krueger
3Cole Wyeth
2Gordon Seidoh Worley
3Cole Wyeth
2Gordon Seidoh Worley
4transhumanist_atom_understander
3Gordon Seidoh Worley
1transhumanist_atom_understander
3Haiku
3Gordon Seidoh Worley
2Richard_Kennaway
2EzzeddineAlSai
3Gordon Seidoh Worley
2Noosphere89
2Gordon Seidoh Worley
2Shankar Sivarajan
2JBlack
2Gordon Seidoh Worley
New Comment
An exponent models things locally, at an appropriate level of detail for modeling them locally. An S-curve won't actually be an S-curve, there will be a lot more data than that in the real thing, omitting the data specifying when the exponent slows down is no different. Simpler models are often more useful, even when you do realize they have a limited scope of applicability.
Your argument doesn't make sense to me. You're saying the exponential models things "locally", but then so can a sigmoid. You say an S-curve won't actually be an S-curve, but neither will an exponential. An exponential function that fits data is not that much simpler than a sigmoid function, and importantly the exponential will be wrong in a non-specific way (we just know that after some unspecified point exponential growth will break down). The sigmoid is at least wrong in a specific way that allows us to say something about where we made a mistake in modeling how growth will end (and because growth always eventually ends, failing to model it is making an incomplete model that clearly confuses a lot of people, because there's no end to people who act as if the growth of something will never end).
This is absolutely true. However, actually using it effectively requires having a sufficiently good, principled reason for thinking the limit is in some particular place, or will be approached on some particular timeline. When I've looked at many (most?) real-world attempts to forecast when some particular exponential will start looking like an s-curve, they're usually really far off, sometimes in ways that 'should' be obvious, even if the forecasting exercise itself is instructive.
Yes, and yet, including the bend is arguably a better model since we know the bend will come. It's hard to get the details of models right, we shouldn't let that be a reason not to get their basic shape right.
Fair enough. If nothing else, it's best to state where you think the min value, max value, and midpoint are, and ideally put error bars around those.
Or, at least, you can state outright you think the midpoint and max are far enough away as to be irrelevant distractions to some particular practical purpose. Or that you expect other factors to intervene and change the trend long before the later parts of the sigmoid shape become relevant.
To add: It is in principle very easy for people to make equivalent prediction errors in either direction about when a particular exponential will level off, and to be wrong by many orders of magnitude. In practice, I usually encounter a vocal minority who happily ignores the fact that the sigmoid even exists, and a larger group who thinks that leveling off must be imminent and the trend can possibly continue much longer. The cynic in me thinks the former group tends to start getting believed just in time to be proven wrong, while the latter group misses out on a lot of opportunities but then helps ensure the leveling off has less catastrophic consequences when it happens.
I'm curious: was there a particular (set of) sigmoid(s) you had in mind when writing this post? And particular opinions about them you haven't seen reflected in discussions?
Most of the times I've used sigmoid in my own modeling/forecasting have been about adoption and penetration of new technologies. Often the width of the sigmoid (say the time to get from 1% to 99% of the way from min to max) is relatively easy to approximate, driven by forces like "how incumbent institutions are governed" (yes, this is critical even for most extremely disruptive innovations). The midpoint and maximum are much harder to anticipate.
In practice, I usually encounter a vocal minority who happily ignores the fact that the sigmoid even exists, and a larger group who thinks that leveling off must be imminent and the trend can possibly continue much longer.
I suspect that most people see what they want to see in models, rather than actually evaluating the models.
I'm curious: was there a particular (set of) sigmoid(s) you had in mind when writing this post? And particular opinions about them you haven't seen reflected in discussions?
No. I just see exponential models literally ever week and they disappointment me because they are leaving out half the model without even a nod to the fact they are doing this. It generally feels like the authors of models are failing to even consider the possibility that the growth of something will end.
I think you’re just not appreciating the usefulness of partial world models.
A sigmoid often looks locally exponential. If the local part is all you can model effectively, your model looks exponential. But it’s a local model. It’s not trying to make claims about the part where the sigmoid flattens out. Why include that part in your model when you don’t have a basis for drawing conclusions about it? It will rather tend to make you more wrong than less wrong :)
Because people look at exponential curves and loose their minds. They see a curve that goes up and to the right forever and think it will never end. People end up making foolish financial and personal decisions that way.
Failing to include an end to a growth curve in the model is a failure to build an adequate model. I see few models of anything using exponentials address when they expect growth to end or clearly indicate that they are addressing only the upward slope of the S-curve.
I think exponentials only feel to some people like they are less wrong than sigmoids because they're failing to count the error at the right end when growth runs out.
You don't have to count error from predictions you don't make. Just put an upper limit on the x axis.
I do feel like this conversation (and all other comment threads) are getting blocked a bit. It may help to distinguish the communicative risks of sharing a plot with an exponential fit and the actual predictive usefulness of locally fitting an exponential. I agree that the former can be a problem, but I think the latter is not. Do we disagree?
I disagree that you don't have to count the error from predictions you don't make. For example, maybe I fail to predict that there will be a market crash next month because I didn't bother to try to make a prediction at all, so I leave all my investments maximally exposed to the market. When my investments are suddenly worth a lot less because I didn't anticipate the market crash, that's an error as far as my net worth is concerned, whether I explicitly made the prediction or not. Maybe I shouldn't lose Bayes points or something, but Bayes points don't pay the rent!
I do feel like this conversation (and all other comment threads) are getting blocked a bit. It may help to distinguish the communicative risks of sharing a plot with an exponential fit and the actual predictive usefulness of locally fitting an exponential. I agree that the former can be a problem, but I think the latter is not. Do we disagree?
I continue to think that the idea of locally fitting an exponential doesn't make sense in most cases where we care about predictive usefulness. If all we care about is fitting a curve to past data, sure, we can always do that. In fact, we can do better than an exponential; we can always find a polynomial that will fit every data point!
The reason to model something using an exponential curve is to make predictions about future data points, in which case the idea of "local" fitting stops making sense, because now we care a great deal about what happens next, and maybe we're almost at the top of a sigmoid, about to level out. I have no problem saying that some particular thing we are modeling may be far from topping out, but if that's the claim we want to make, we should offer a theory for why we believe it's far from topping out, not just throw up our hands and say "idk man, i can't figure it out, guess i'll just use an exponential", which is what many exponential curve models I see effectively do.
One can model a local part of the future, not just the past.
Here’s a related example. If I know the spring constant of some material, I can model the force as linear in displacement. I know that it is not truly linear in displacement, but that is still a useful simplified model that allows an analytical solution and works well in some reasonable local neighborhood - and I might not know exactly where it breaks down! I can still use the approximation if I don’t know exactly where it breaks down. And I don’t actually know the math that describes precisely where it breaks down, so trying to add it to the model would probably just result in saying something wrong - it might even mess up my LOCAL predictions.
I don’t think that you would burst into an undergraduate physics class and say “why are you using this first order differential equation?? In reality, pulling a spring far past the breaking point will cause the spring ‘constant’ to decrease! It’s not really a constant! It is NEVER really a constant! This model is making you more wrong!”
Rather, the professor should say the following sentence: “the linear model is an approximation that works for small displacements.”
When it comes to springs, someone (not me) does know math that reasonably well models where the linear approximation breaks down for a given material. For scaling laws, we don’t even know that math.
Ironically, I have a 250 dollar bet on with Kokotajlo that task lengths will scale (quite) sub exponentially because I believe that the sigmoid runs out soon, for a long list of concrete reasons that apply to this specific case. But NOT because I’m actually fitting a sigmoid.
Yes, this all seems quite reasonable, and I think it's a failure if we fail to at least acknowledge that the model is going to break down at some point and give some guesses about when it will break down, which is what I see happening a lot when I read about exponential growth models (the modeler presents a curve, but not a model or even of theory of how growth might end, which to me feels like I'm only getting half a model, and it makes the model not very useful because it has such limited predictive power and it's not even attempting to quantifying the limitations).
Like I'm okay with saying we don't know how to quantify something at all, but once we start quantifying, I expect to see the quantifying carried through. Making a bet is a great way to quantify!
Low effort, low nuance hot take:
Sigmoids are fake. Real curves aren't symmetrical, and research progress curves in particular tend to look like exponentials that run into brick walls. Adoption curves can be relatively balanced but I still don't buy it.
And given you already can't fit a sigmoid that isn't already dying and probably shouldn't try, fitting the thing that actually happens in reality is doomed. Fit your exponential and intuit the rest. You don't actually have quantified evidence for when it ends, so use the evidence you do have instead.
This reads to me like a fully generalized argument against numerical modeling.
After all, exponentials are also fake. You can't be guaranteed to fit a exponential to a data set that has more than two data points. Maybe just fit a linear regression and intuit the rest. Only, the linear regression doesn't fit perfectly either, so maybe just go on intuition all together.
We know that growth always ends. If you think it won't look like a sigmoid, perhaps another function that levels out. But the exponential is guaranteed to be wrong in the long run, so why not simply give a wide range for some of the parameters or give multiple models of what could happen?
It's only an argument against fitting curves to noise. Rather than explain, it turns out there's already a post that puts this better than I could hope to. I endorse it fully.
https://www.lesswrong.com/posts/6tErqpd2tDcpiBrX9/why-sigmoids-are-so-hard-to-predict
Yes, let's not fit to noise, but fitting to an exponential is also fitting to "noise" in the sense that it's fitting to a growth pattern that long run is wrong.
If not the sigmoid, there are other functions that produce S-curves that can be used like Gompertz function and the Bass diffusion model. These address some of the issues with sigmoids.
But I also find arguments about modeling being hard fall flat for me. Yes, of course it is hard. Exponential models make one kind of extremely obvious error. Sigmoids make another kind of error. It's not that hard to at least have a piece-wise model that says "yes, our model predicts growth will end around here" even if that's hard to fit into a single function, and I see little benefit to not doing that (other than it's hard and people don't want to or they are incentivized to do the easy thing and show a model that keeps going up).
The point of a model is to be validly predictive of something. Fitting your exponential is validly predictive of local behaviour more often than not. Often, insanely so.[1] You can directly use the numerical model to make precise and relevant predictions.
Your exponential doesn't tell you when the trend stops, but it's not trying to, for one because it's incapable of modelling that. That's ok, because that's not its job.
Fitting a sigmoid doesn't do this. The majority of times, the only additional thing the result of a sigmoid fit tells you is how an arbitrarily chosen dampening model fits to the arbitrary noise in your data. There's nothing you can do with that, because it's not predictive of anything of value.
This doesn't mean you shouldn't care about limiting behaviour, or dampening factors. It just means this particular tool, fitting a numerical model to numerical data, isn't the right tool for reasoning about it.
- ^
“I answered that the Gods Of Straight Lines are more powerful than the Gods Of The Copybook Headings, so if you try to use common sense on this problem you will fail.” — Is Science Slowing Down?, Slate Star Codex, https://slatestarcodex.com/2018/11/26/is-science-slowing-down-2/
Whilst technically true, those who attempt to use this fact to predict future growth tend to end up just as wrong as those who don't.
All exponentials end, but if you don't know when you need to prepare equally for the scenario where it ends tomorrow, and the one where it ends with the universe in paperclips.
Whilst technically true, those who attempt to use this fact to predict future growth tend to end up just as wrong as those who don't.
Then why not use it, because at least their curve will have the right shape and they will be slightly less wrong than those who don't acknowledge that growth eventually ends, even if the end of that growth is very far off.
Because it has the wrong shape in every way that matters if they draw an s curve with us at the halfway point (which seems to be the natural failure mode), and they're actually at the 1 percent mark. The s curve isn't particularly illuminating over simply saying this exponential will stop at some point but we don't know when, but unfortunately tends to lend itself to overconfident predictions.
Failing to acknowledge that growth will end also leads to overconfident predictions. I'm not making an argument in favor of bad predictions. I'm making an argument in favor of not making an extremely obvious mistake when modeling reality.
Your complaining about how the graph is drawn, and hope to fix that by drawing a graph that is almost certainly wrong? At least the graph they drew only relies on actual past data.
I agree they would do better to acknowledge that whilst the growth is currently exponential, it will have to stop at some point but we have no idea when. That gets a bit tiring after a while though.
I agree they would do better to acknowledge that whilst the growth is currently exponential, it will have to stop at some point but we have no idea when. That gets a bit tiring after a while though.
And yet, people keep forgetting this basic fact so aggressively that I think they need to be aggressively reminded of it, even if it feels tiring.
Yes, if you want to model growth, you probably want something like a sigmoid or Gompertz curve, whose value approaches some limit rather than rising infinitely forever.
But if you want to actually draw that curve, and use it to predict effects that you care about, you need to know what limit it approaches.
Whether that curve approaches 1 or 10^100, is going to matter a lot.
Yes, this is true, and I think modelers are cowards for not making a guess.
(I'm only being a little hyperbolic here. Lots of people are deathly afraid of being wrong, and so I have a suspicion that many modelers are drawn to exponentials because they have to model less stuff and when the exponential runs out they can just shrug it off because they didn't make a specific prediction about when growth would end.)
It's possible to fit data points to an S-curve without assuming where it flattens out — but then you might not draw the limit as part of your prediction. We don't want to assume the thing can grow forever; the market saturates somewhere, even if we don't know where.
Like, if you're forecasting traffic growth for a web service, you know that there's a finite amount of human attention that can be spent on looking at web pages. It might be a lot higher than anyone expected, but it's not infinite.
See for instance Wikipedia's growth models (sadly not updated since 2015) — they started out with an exponential model and then ended up with Gompertz being much more accurate.
This comment makes me think the conversation can’t usefully continue on the object level - your wider beliefs about rationality seem to depart from mine pretty far.
Why does it seem good to you to provide incomplete models that we know are incomplete and fail to acknowledge that incompleteness, because that's how most exponential models of growth look to me?
This is a strawman. Essentially everyone acknowledges the incompleteness.
The AI 2027 guys expect it to go super exponential.
I expect it to go sigmoid.
We both say this loudly and frequently.
EDIT: actually you may have a point about “situational awareness”
Yes, some people are more careful than others.
I'm on Twitter all day. People love charts that go up and to the right. Feels like every week I see multiple tweets from people model some growth process, usually related to AI, with a naive exponential and no consideration of the fact that growth ends.
I saw enough of these that yesterday it finally clicked that I should write this post.
You say "if we are to accurately model the world"...
If I am modelling the path of a baseball, and I write "F = mg", would you "correct" me that it's actually inverse square, that the Earth's gravitation cannot stay at this strength to arbitrary heights? If you did, I would remind you that we are talking about a baseball game, and not shooting it into orbit—or conclude that you had an agenda other than determining where the ball lands.
What if I'm sampling from a population, and you catch me multiplying probabilities together, as if my draws are independent, as if the population is infinite? Yes there is an end to the population, but as long as it's far away, the dependence induced by sampling without replacement is negligible.
Well, that's the question, whether to include an effect in the model or whether it's negligible. An effect like finite population size, diminishing gravity, or the "crowding" effects that turn an exponential growth model logistic.
And the question cannot be escaped just by noting the effect is important eventually.
For most growth curves, the effect is important on reasonable time scales. Most of the time we're trying to model something where growth will run out in years or decades (though perhaps to be replaced by another S-curve due to innovation).
For example, it should have been obvious to everyone that LLM scaling was on an S-curve, and that scale alone would run out of gains and we'd have to start looking for gains from sources other than scale. That many modelers before 2025 thought that LLM gains could go on forever from scaling alone is a failure of their models. Had they even tried to model when scaling would run out, they could have better anticipated when future growth in capabilities would have had to come from other sources. But most models I saw didn't even attempt this.
I'm surprised at how hard it is for me to think of counterexamples.
I thought surely whale populations due to the slow generation time, but it looks like humpback whale populations have already recovered from whaling, and blue whales will get there before long.
Thinking again—in my baseball example, gravity is pulling the ball into the domain of applicability of the constant acceleration model.
Maybe what's special about the exponential growth model is it implies escape from its own domain of applicability, in time that grows slowly (logarithmically) with the threshold.
Communication is about other people. It is the thoughts that we put into other's heads, not the precise content of the propositions themselves. The graphs and other symbols we choose to use should put more likely-correct and contextually relevant thoughts into other people's heads.
If I am communicating with someone because I believe their lack of information gives them an insufficiently aggressive model of past (and therefore probably future) AI capabilities progress, then the only reason I can think to use the sigmoid graph is to head off this specific criticism so that they are not distracted by the actual content of the communication. If I did make this choice, I would also want to put a cut in the y axis and cheekily label the upper value with something to indicate that it may be far beyond what they are currently entertaining to be possible.
I often do make this choice when verbally communicating. e.g. "Of course, it has to level off at some point, but that could very well be several orders of magnitude above human capability." If I have exactly one image and no chance to elaborate, for most audiences, a sigmoid probably does a poorer job of putting correct and relevant thoughts into their heads than an exponential.
If I have exactly one image and no chance to elaborate, for most audiences, a sigmoid probably does a poorer job of putting correct and relevant thoughts into their heads than an exponential.
I am sympathetic to this line of argument. I agree that if I was showing a chart to a politician, I might not want to show them that they curve levels off, because if my goal is to get them to act on the basis of rapid growth that is exponential for a while resulting in dangers that need to be urgently responded to, I don't have time for them to be thinking about when that growth ends because it might muddy the waters and make them less likely to act.
But then this isn't really an accurate model anymore, it's a model crafted to convince someone, to tell a version of what you believe that is persuasive to some end.
Not many S-curves here, except the imaginary ones hand-drawn over the data:
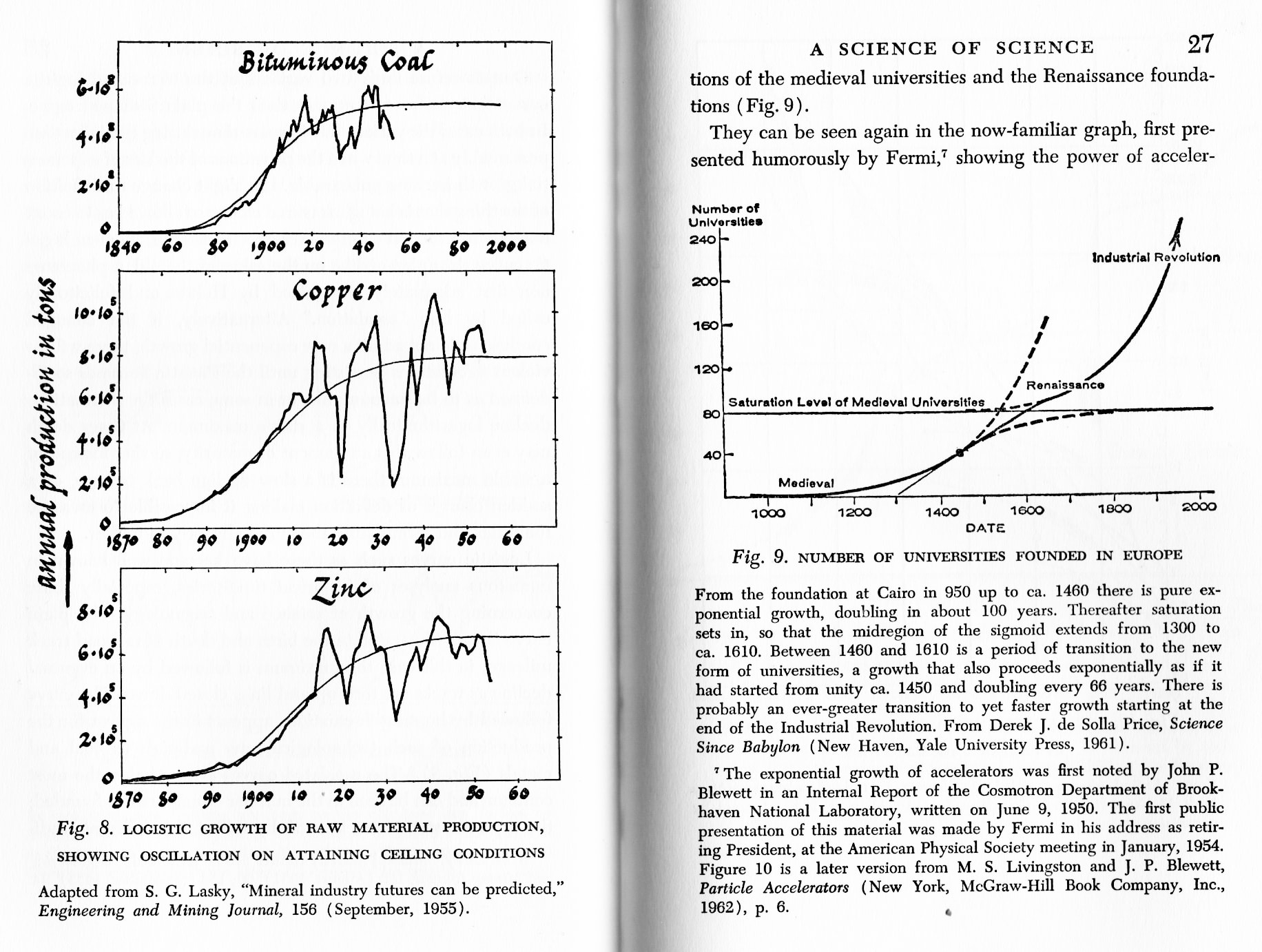
From "Little Science, Big Science" by Derek de Solla Price, 1963, pp.26-29.
Nor here:
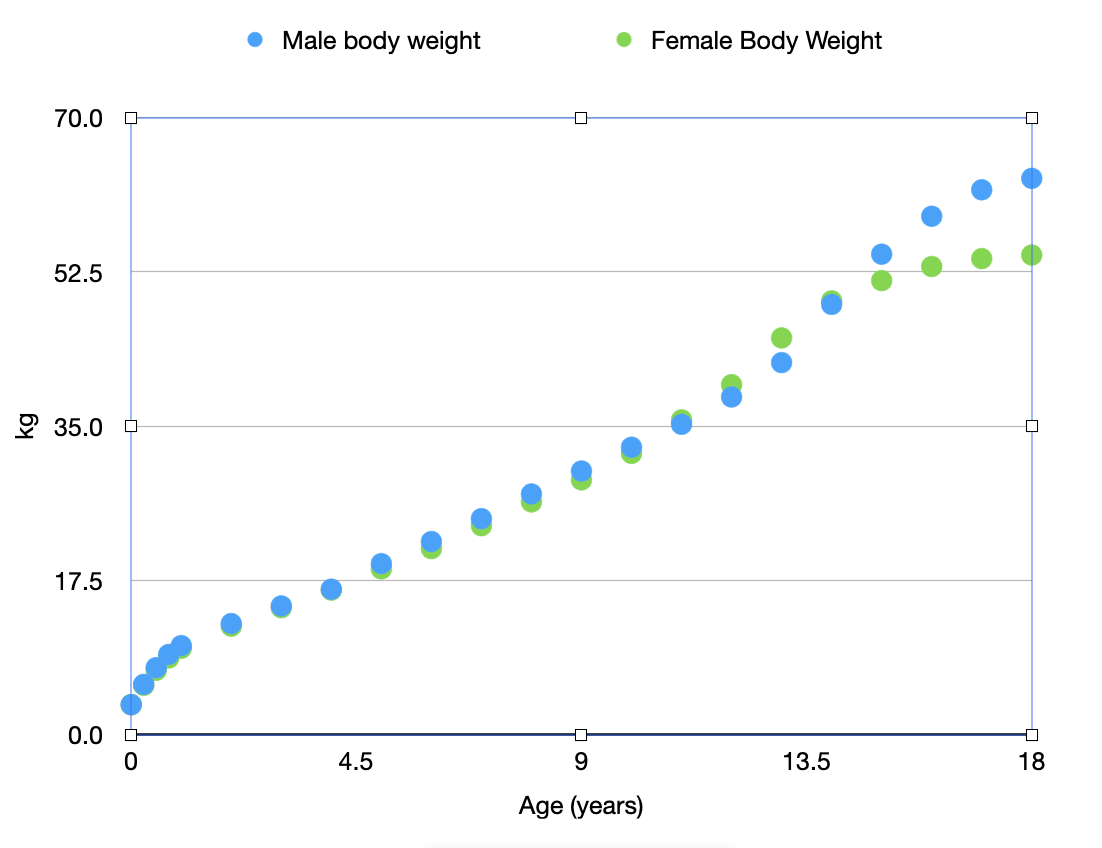
Data plotted from table 1 of Sami Haddad, Concetta Restieri & Kannan Krishnan (2001): "Characterization of age-related changes in body weight and organ weights from birth to adolescence in humans".
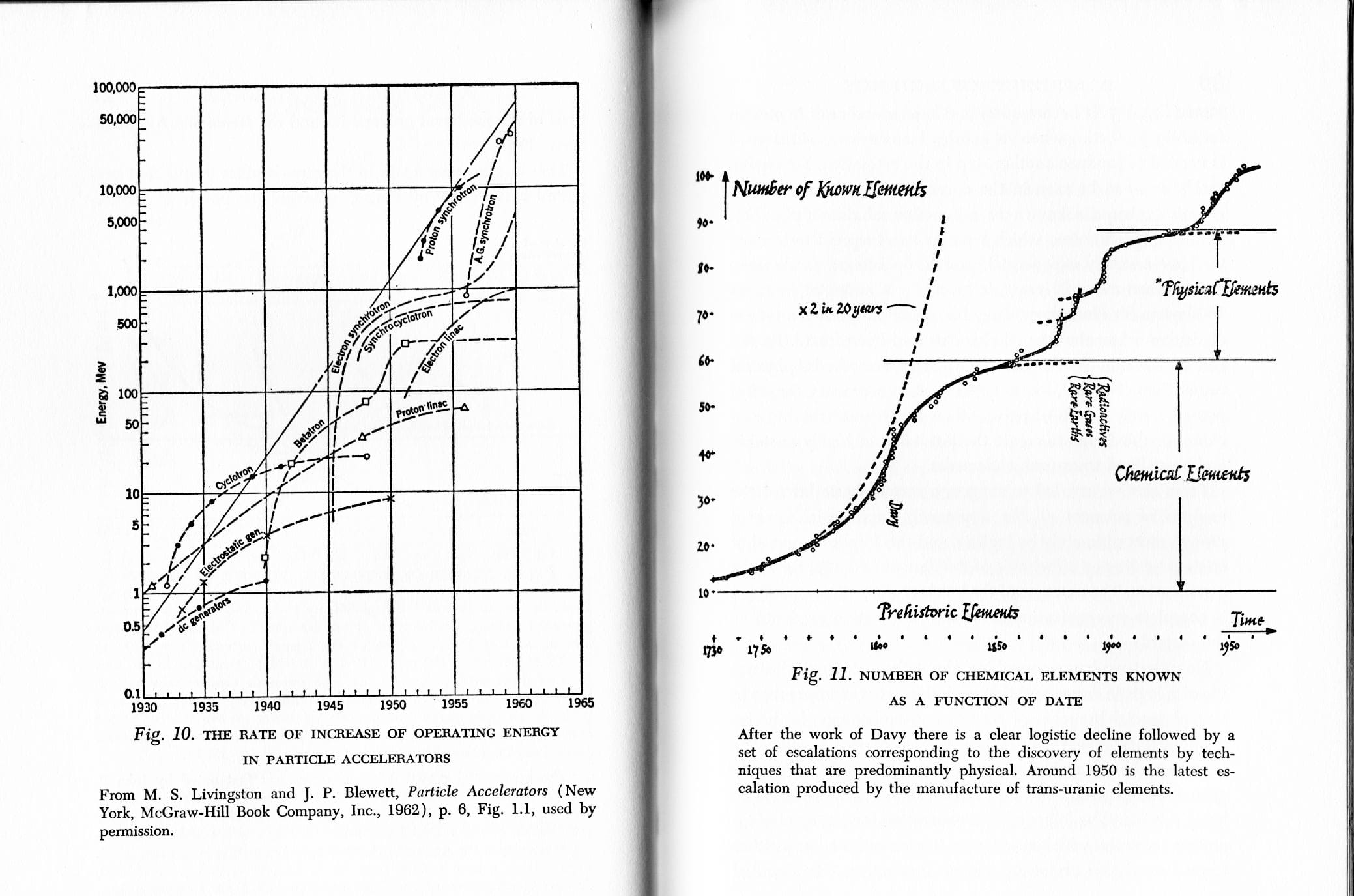
Then of course there is Moore's Law (variously formulated), which people kept prematurely predicting the end of, and indeed clock speed stalled, but FLOPS nevertheless has been on an exponential track at least to 2017.
And there is a notable graph comparing "experts'" predictions of the future of something or other that over an extended period of time predicted that now it's going to flatten, when it just kept on going up. I don't remember enough details to track that one down.
It's easy to predict that an exponential will end, next to impossible to predict when or how. Nice, symmetrical business-as-usual-during-alterations logistic curves are not the rule, and the end is not to be found in the beginning.
But which S curve? People like exponentials because of the differential equation they satisfy. To choose a type of S curve you're implicitly choosing a differential equation and you have justify that choice.
Yes, just as the choice of an exponential should be justified.
Most research papers at least do this as far as explaining why pick an exponential over a linear regression, which I think is a good practice because in many applications picking something other than a linear regression results in better fit of past data but worse fit of future data. But the point stands that needing to justify a sigmoidal or sigmoid-like model is the same problem as justifying the choice of an exponential.
I agree that all exponentials eventually end, but I don't think this matters that much, because trying to predict the future using sigmoids/functions that don't grow without bound is also very hard, and you need to have very good priors or very low noise data to not be very off, so an exponential is usually a better fit unless you have reason to believe you've identified a specific upper bound and the dampening term:
Why sigmoids are so hard to predict
Sigmoids behaving badly: why they usually cannot predict the future as well as they seem to promise (paper)
A key crux is I basically disagree with the assumption that you can reliably detect either the dampening term or the upper bound in early data, because I expect real-life data to be far too noisy to figure both of these out, and this is especially the case in AI.
There are special cases like disease modeling (though even there predictions can be wildly off), but in general I think the exponential fit is almost always better than a sigmoid/function that doesn't grow without bound unless you have strong reason to believe you've identified both the dampening term and the upper bound.
There are special cases like disease modeling (though even there predictions can be wildly off), but in general I think the exponential fit is almost always better than a sigmoid/function that doesn't grow without bound unless you have strong reason to believe you've identified both the dampening term and the upper bound.
I find these arguments about fit strange, like they are failing to remember what we're trying to do with predictions.
We want to have an accurate model of the future. That exponentials fit data better is nice, and maybe they are easier to predict the next point under many circumstances, but they are leaving something out.
Like suppose I'm trying to predict if I'll be alive tomorrow. I could have a naive model that predicts I will be because I was alive every previous day. But this model is wrong in a very important way: one day I will die! That the model fails to account for this fact makes the model less useful, because even if it's right for a long time, eventually it won't be, and it's a failure of the model that I'd get surprised to be dead.
This argument works just as well for exponential decay: it's "always the wrong model" because no decay lasts forever, eventually you'll run out of atoms in your radioactive sample (or whatever else you're modeling), and so some other curve that intercepts the y-axis in finite time is a better model because it gets the "basic shape" right and doesn't make "an extremely obvious mistake when modeling reality."
Some curves that start exponential are actual unimodal, in the long run. Some are oscillatory. Some are chaotic, some have undefined behaviour because the thing being plotted ceases to make sense.
Why do you think all of them are eventually S curves in particular?
Fair point!
A more accurate statement would be that most exponentials are eventually sigmoids, while others are some other non-exponential function. A shorter version would be that no seeming exponential goes on forever.
That said, almost everything I can recall seeing poeple model as an exponential turned out to be a sigmoid.
Curated and popular this week