Given the complexity of the ruleset my model was entirely too simple. I assumed that higher stats are always better, and that the probability of success was proportional to #success|stat / #entries|stat (with an additional pseudo count each for success and failure to reduce overfitting).

Nevertheless, I got lucky in that I happened to end up in the region of optimal solutions

STR: 8/20 
CON: 15/20
DEX: 13/20
INT: 13/20
WIS: 15/20
CHA: 8/20

The result of my adventure was

You fail to complete your Great Quest.

(you had a 93.75% chance of success.)

Cheers to simon, ericf and myself, for offering an optimal solution! And cheers to abstractapplic for organizing the challenge.

The leaderboard (if you're not here, I couldn't figure out what your final decision was, or you added more than 10 points):

simon, ericf 0.9375 

[('CHA', 8), ('CON', 15), ('DEX', 13), ('INT', 13), ('STR', 8), ('WIS', 15)]

seed 0.9375 

[('CHA', 8), ('CON', 14), ('DEX', 13), ('INT', 13), ('STR', 8), ('WIS', 16)]

Samuel Clamons 0.8095 

[('CHA', 8), ('CON', 17), ('DEX', 13), ('INT', 13), ('STR', 7), ('WIS', 14)]

Asgard 0.7857 

[('CHA', 9), ('CON', 16), ('DEX', 14), ('INT', 13), ('STR', 8), ('WIS', 12)]

Measure 0.7308 

[('CHA', 8), ('CON', 14), ('DEX', 13), ('INT', 13), ('STR', 6), ('WIS', 18)]

kiwiakos 0.6774 

[('CHA', 7), ('CON', 15), ('DEX', 13), ('INT', 13), ('STR', 6), ('WIS', 18)]

Alexey 0.6500

  [('CHA', 11), ('CON', 14), ('DEX', 13), ('INT', 13), ('STR', 6), ('WIS', 15)]

newcom 0.6471

  [('CHA', 11), ('CON', 16), ('DEX', 13), ('INT', 13), ('STR', 7), ('WIS', 12)]

AABoyles, Pongo, GuySrinivasan 0.6389 

[('CHA', 6), ('CON', 14), ('DEX', 13), ('INT', 13), ('STR', 6), ('WIS', 20)]

Yongee 0.6364 

[('CHA', 5), ('CON', 14), ('DEX', 13), ('INT', 20), ('STR', 8), ('WIS', 12)]

Deccludor 0.6098 [('CHA', 5), ('CON', 20), ('DEX', 13), ('INT', 13), ('STR', 6), ('WIS', 15)]

Randomini 0.4688 [('CHA', 4), ('CON', 14), ('DEX', 13), ('INT', 13), ('STR', 16), ('WIS', 12)] 
 

From plotting the data, I saw that:

• looked like the stats were independtly randomly generated and cut off at sum >= 60.
• dexterity was useless
• looked like there was a big advantage to having stats >= 8. For strengh, strength=8 was almost as good as strength=20

I fit a regularized logistic regression and a neural net, but couldn't get validation accuracy greater than 70%, which was only a little better than the 65% baseline of random guessing. I realized that the data is not very informative and I don't know how results are calculated, so I better stick with a conservative model like Nearest Neighbors classifier, and try a few different models. I fit a KNN classifier, gradient boosting on decision trees, and regularized logistic regression (all with validation accuracy 70%), and chose a point which gave near the top scores for all three classifiers. (It had all stats >=8, too.)

What I did was use Excel to make 9 graphs: "% successful" vs. each stat individually, "highest stat," "lowest stat," and "total stats" under the assumption that there would be some sort of mapping of stats -> success, but that there wouldn't be any dependencies between stats -whoops-!

The discontinuities at 8 STR & CHA were visually obvious, as was the negative slope of Dex... I actually inverted everyone's DEX (trueDEX = 22 - givenDEX] for the highest/lowest/total graphs. The data also showed big gains in the 12-16 range for CON and WIS, so that's where I put the extra points.

This was cool! Definitely looking forward to the next challenge and using what I learned from this.

I got 70% chance of success, and succeeded with these stats and strategy.

thanks for making this, it was a lot of fun! Would love to have a go at your next challenges :)

Well, I think that the Neural Net and Decision Forest I used in the last post both saw pretty much what you were going for; with the exception that they both put one too many points into CHA, bumping it up to 9, instead of into WIS.

All in all, a success for throwing lots of data into an ML model you don't fully understand and walking away... except that I had two other models which performed abysmally. 

If you didn’t account for selection effects, you may have correctly avoided boosting DEX because you thought it was actively harmful instead of merely useless. 

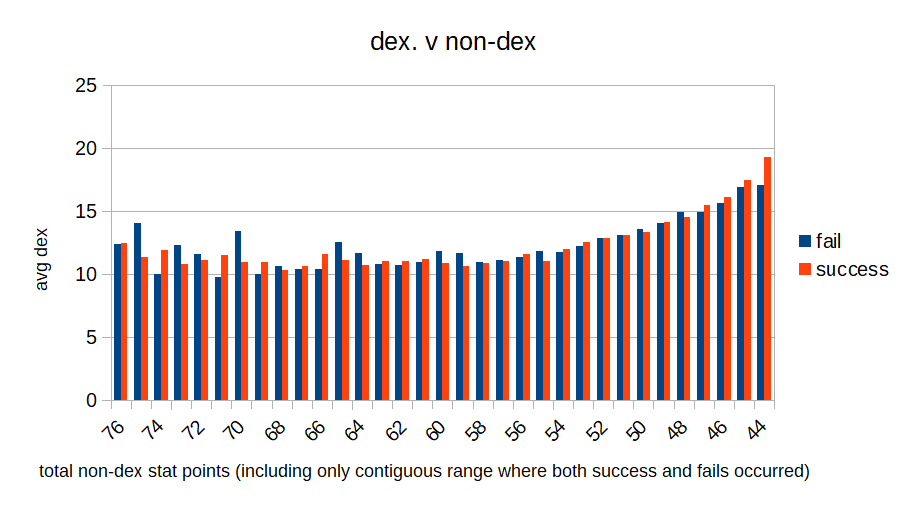
I immediately considered a selection effect, but then I tricked myself into believing it did matter by a method that corrected for the selection effect but was vulnerable to randomness/falsely seeing patterns. Oops. Specifically I found the average dex for successful and failed adventurers for each total non-dex stat value, but had them listed in an inconvenient big column with lots of gaps. I looked at some differences and it seemed that for middle values of non-dex stats, successful adventurers consistently had lower average dex than failed ones, while that reversed for extreme values. When I (now - I didn't at the time) make a bar chart out of the data it's a lot more clear that there's no good evidence for any effect of dex on success: 

If you didn’t look for interactions, you may have dodged the WIS<INT penalty just because WIS seemed like a better place to put points than INT. 

Yep. Thing is, I *did* look for interactions - with DEX. I had the idea that DEX might be bad due to such interactions, and when I didn't find anything more or less stopped looking for such interactions.

And I’m pretty sure even the three people who submitted optimal answers on the last post (good job simon, seed, and Ericf) didn’t find them by using the right link function

For sure in my case. I calculated the success/fail ratios for each value of each stat individually (no smoothing), and found the reachable stat combo that maximized the product of those ratios. This method found the importance of reaching 8. I was never confident that this wasn't random, though.

When I did later start simming guesses what I simmed would have given smoothed results: a bunch of stat checks with a D20, success if total number of passed stat checks  greater than a threshold. The actual test would have been pretty far down in the list of things I would have checked given infinite time.

I failed, but at (WIS +6, CHA +4) I had a 73.07% chance for success, which I think is at least a local maximum.

Actually adding even 1 point to STR is an improvement, though not as much as STR +2.