This book (available as a free pdf here) is one of the foundational texts for Rationalists; Eliezer refers to Jaynes as The Level Above Mine. While we agree that Jaynes is very lucid and the book is wonderful, we also think the book's target audience are graduate physics students. It occupies a sparse area of the literature, between statistics, math, causality, and philosophy of science that contains real, practical lessons about how to think about the world and its uncertainty. Here, we will try to give a review where we share the core insight of the book while skipping all the integrals and derivations. The book is basically 50% high level math and 50% cool stories and rants that you can mostly understand without the math. It also covers a lot of material, and this review covers just the first 6 chapters, which introduces the fundamental concepts and problems.

The book has 2 parts:

• Part I (Chapter 1-10): Principles and elementary applications
• Part II (Chapter 11-22): Advanced applications

This is a review of chapters 1-6

Part 1: A new Foundation of Probability Theory

The first two chapters of the book are by far the toughest. In chapter one, Jaynes gives a half chapter refresher of formal logic, and introduces the concept of probability as logic. Here the goal is to extend the rules of formal logic such that they also apply to probabilistic reasoning. This is a complicated task: going from strict binary truth values to continuous probabilities without assuming anything about what a probability is. This is also where the book gets its name, the logic of science, because much like Eliezer, Jaynes views reasoning under uncertainty as the foundation of science.

Chapter 1: Plausible Reasoning

Jaynes opens the chapter with the following:

Suppose some dark night a policeman walks down a street, apparently deserted. Suddenly he hears a burglar alarm, looks across the street, and sees a jewelry store with a broken window. Then a gentleman wearing a mask comes crawling out through the broken window, carrying a bag which turns out to be full of expensive jewelry. The policeman doesn’t hesitate at all in deciding that this gentleman is dishonest. But by what reasoning process does he arrive at this conclusion? Let us first take a leisurely look at the general nature of such problems.

In formal logic we have statements such as "If A, Then B; A is true, therefore B is true". This is called a strong syllogism. Here is an example (with premises above the line and conclusion below):

IF Fisher dies before age 100, then he died a Frequentist
Fisher died at the age of 72
———————————————————————————————————
Fisher died a Frequentist

This however does not work for the story Jaynes gave about the burglar, which requires a weak syllogism.

Jaynes wants to formalize weak syllogisms, and does that by imagining building a robot that can output the plausibility of an outcome, updating on some data. The actual implementation is up to the builder, but it should fulfill three desiderata that allows for solving the problem. These are, note here that Jaynes uses the word "plausibility" because he has not gotten far enough with the formalism to define what a probability is, but we can think of these as probabilities:

1. Degrees of plausibility are represented by real numbers.

2. Qualitative correspondence with common sense.

3. Consistency

   a. If a conclusion can be reasoned out in more than one way, then every possible way must lead to the same result.

   b. The robot always considers all of the relevant evidence that it has access to, for any given question.

   c. The robot always represents equivalent states of knowledge by equivalent plausibility assignments.

The motivation for building a robot is that this can be an objective, computational method that is compatible with human intuition including the weak syllogism.

The first desiderata is easy to understand, the second one is basically that the rules we derive should be "numerically sorted as expected," so if A is evidence of B, then $A\mid B$ should be larger than $A$, if we choose $\mid$ to mean "information about" The third desiderata has 3 components. 3.a) is that all paths from evidence to conclusion should resolve to the same number, so knowing that an unknown person has a beard and red cloth or red cloth and a beard should make the robot end up in the same state of knowledge. 3.b) is a very Bayesian point, that says that all background information regarding the problem should be applied, a common example is that temperatures (in Kelvin) cannot be negative, so we know a-priori that we should assign zero probability mass to negative temperatures, sometimes this makes the math very complicated, but that is "the ideal robots problem" not ours. 3c) means that the same probability will always mean the same level of certainty.

As of Chapter 1, it’s not clear that the robot is optimal, but there is potential for its reasoning to match ‘common sense’.

Chapter 2: The Quantitative Rules

After Chapter 1 we can make logical statements. We also have 3 desiderata from the previous chapter, and are left with the question, what more do we need for our robot to make inferences? It turns out we only need two things, the product rule and the sum rule.

This chapter is the driest in the book, because it contains all the math needed to derive the chain and product rules of probability, while this might be tedious, the amazing thing going on here is that after 2 chapters Jaynes has a more solid version of probability theory than the Kolmogorov axioms without using measure theory. This is achieved by bridging a connection between logical statements like ‘B is true given C’ into probability with two rules that we summarize here.

What we want are rules to connect the rules of logic to mathematical functions so we can make statements such as

Late fisher introduced fiduciary probabilities which are are inverse probabilities
Posteriors are inverse probabilities
——————————————————————————————————————————————————————————————————————
It is likely that Fisher would have eventually ended up a Bayesian.

The product rule is the first of the 2 rules we need. It is introduced by appealing to desideratum 3a. By noting that receiving the information A, and then information B should put us in the same state of knowledge, as would getting the information in the opposite order:

We first seek a consistent rule relating the plausibility of the logical product AB to the plausibilities of A and B separately. In particular, let us find $AB\mid C$. Since the reasoning is somewhat subtle, we examine this from several different viewpoints.
As a first orientation, note that the process of deciding that AB is true can be broken down into elementary decisions about A and B separately. The robot can

1. decide that B is true; ($B\mid C$)
2. having accepted B as true, decide that A is true. $(A\mid BC)$ Or, equally well,
3. decide that A is true; $(A\mid C)$
4. having accepted A as true, decide that B is true. $(B\mid AC)$

Note that Jaynes here uses the $A\mid C$ instead of the $p(A\mid C$) notation we are used to in modern statistics, because at this point in chapter 2 he is in the process of reinventing all of probability theory and statistics including the basic ‘p’ operator! Spoiler alert, using a lot of tedious math (that we honestly do not fully follow), we end up with ye old product rule:

$$p\left(AB\right)=p(A\mid B)p\left(B\right)=p(B\mid A)p\left(A\right)$$

Or as Jaynes prefers it:

$$p(AB\mid C)=p(A\mid BC)p(B\mid C)=p(B\mid AC)p(A\mid C)$$

Note that Jaynes has a habit of always slapping on an extra conditional $p(AB\mid C)$ instead of $p\left(AB\right)$to emphasize that $p\left(AB\right)$ is a probability subject to whatever background information (prior knowledge) you have available to you, for him the concept of $p\left(A\right)$ makes no sense, as it suggests a probability independent of any information.

The Sum rule is basically that since A and not A is one ($A+\overline{A}=1$), then

$$p(A\mid B)+p(\overline{A}\mid B)=1$$

This chapter also introduces the principle of indifference which roughly states that given N possible outcomes with no prior information, they are all equally plausible. Up to this point, Jaynes has been using ‘plausibility’ as a measure for discussing outcomes. At the end of this chapter he introduces the original definition of probability from Bernoulli (1713), the classical example of drawing balls from a (Bernoulli) urn as a ratio of the ball counts in the urn. So probability is a concrete, convenient, normalized quantity that is related to the more general notion of plausibility.

With these rules and definition of probability, Jaynes now revisits the robot, which takes in information and outputs probabilities (instead of plausibility) for different outcomes to show the objective/deterministic property.

“Anyone who has the same information, but comes to a different conclusion than our robot, is necessarily violating one of those desiderata.”

This seems obvious for the case where you have no information (e.g. with the Bernoulli urn case, assigning probabilities of each ball being picked), but initially feels problematic for the other cases where indifference doesn’t apply (e.g. you have side information that one of the balls is twice as large). People that try to follow the robot’s rules might come out with different concrete values for each ball for this case. But the problem is now conditional on much more than the size of the ball, but rather the person’s individual beliefs about how size of the ball increases likelihood of selection. The advantage of the robot is that it requires clearly specifying those priors, and the idea is if two people shared the same priors, they would converge on the same solution. Of course, in practice, we can never write all of our priors for most problems, but the principle is still useful for understanding how we would like to come up with posterior probabilities for complicated problems. It is interesting to note that Jaynes uses the word prior in a much broader sense than most Bayesian statisticians and rationalists, for example the likelihood/sampling function we use when performing a Bayesian update is prior information for Jaynes. If you come from information science (like one of us) then it is obvious that he is right, if you come from statistics (like the other of us), then this is immensely confusing at first, but it makes it easier to understand the concept of maximum entropy.

Part 2: Basic Statistics reinvented

Chapter 3: Elementary sampling theory

Sampling theory is the foundation of classical or frequentist statistics. It concerns itself with “forwards probabilities” of the type if a urn has 5 white and 5 red balls, what is the probability of sampling (drawing) 2 white. This chapter rederives all the standard coin like distributions using the rules from chapter 1 and 2. Jaynes makes 2 interesting observations in this chapter:

Logic vs. Propensity:

When Jaynes wrote this chapter people were much more confused about causality than we are today. And philosophers like Penrose “takes it as a fundamental axiom that probabilities referring to the present time can depend only on what happened earlier and, not what happens later”, thus the two following scenarios are very different:

• my first draw from an urn was a red ball; what is your guess for the color of the second?
• my second draw from an urn was a red ball; what is your guess for the color of the first?

However when we use probability as logic, we do not care about causality, only about how the information available to changes our beliefs, and in the above case knowing that the second or first ball is red contains equal information about the urn, which in turn gives equal information about information about the unknown draw (whenever it happened). In Judea Pearl's notation this propensity vs logic is solved by introducing a new syntax, where $P(A\mid B)$ is the information B gives about A (as above) and the new notation $P(A\mid do(B\left)\right)$ is how “doing B” (rather than knowing B) changes A.

Reality vs. Models:

Jaynes is a physicist and therefore cares about the real world, not the idealized world of mathematical models. If you are drawing from a real urn then the size and shapes of the balls and urn matter for inference, so should we model the physics of the balls? Here is Jaynes's thoughts on the matter:

In probability theory there is a very clever trick for handling a problem that becomes too difficult. We just solve it anyway by:

1. making it still harder;
2. redefining what we mean by ‘solving’ it, so that it becomes something we can do;
3. inventing a dignified and technical-sounding word to describe this procedure, which has the psychological effect of concealing the real nature of what we have done, and making it appear respectable.

In the case of sampling with replacement, we apply this strategy as follows.

1. Suppose that, after tossing the ball in, we shake up the urn. However complicated the problem was initially, it now becomes many orders of magnitude more complicated, because the solution now depends on every detail of the precise way we shake it, in addition to all the factors mentioned above.
2. We now assert that the shaking has somehow made all these details irrelevant, so that the problem reverts back to the simple one where the Bernoulli urn rule applies.
3. We invent the dignified-sounding word randomization to describe what we have done. This term is, evidently, a euphemism, whose real meaning is: deliberately throwing away relevant information when it becomes too complicated for us to handle.

We have described this procedure in laconic terms, because an antidote is needed for the impression created by some writers on probability theory, who attach a kind of mystical significance to it. For some, declaring a problem to be ‘randomized’ is an incantation with the same purpose and effect as those uttered by an exorcist to drive out evil spirits; i.e. it cleanses their subsequent calculations and renders them immune to criticism. We agnostics often envy the True Believer, who thus acquires so easily that sense of security which is forever denied to us. … Shaking does not make the result ‘random’, because that term is basically meaningless as an attribute of the real world; it has no clear definition applicable in the real world. The belief that ‘randomness’ is some kind of real property existing in Nature is a form of the mind projection fallacy which says, in effect, ‘I don’t know the detailed causes – therefore – Nature does not know them.’ What shaking accomplishes is very different. It does not affect Nature’s workings in any way; it only ensures that no human is able to exert any wilful influence on the result. Therefore, nobody can be charged with ‘fixing’ the outcome.

Chapter 4: Elementary hypothesis testing

The previous chapter was about forward probabilities where we reason from hypothesis (H) to data (D), we write that as $P(D\mid H)$. But very often we have observed data and want to reason back to the phenomena that gave rise to our data, $P(H\mid D)$.

This is sometimes called reverse probability because we are reversing the D and H in the conditional probability, it is also sometimes called hypothesis testing as we want to see which hypothesis fits the data.

Priors

In order to flip or reverse the probability we need a prior. Jaynes imagines the robot as always having information X available where X is all the robot has learned since it rolled off the factory floor, so what we want is not:

• $P(H\mid D)$: What the data makes us believe about H, but
• $P(H\mid XD)$: What the data and our prior knowledge makes us believe about H.

Any probability $P(H\mid X)$ that is only conditional on X is a prior probability. It is important to note that it is prior in “information/logic” not prior in “time/causality”, as there is no time variable in information theory.

The prior information is simply the part of the information we have not rolled up in the data variable, and it can sometimes be arbitrary what is prior and what is data, your current posterior is your next experiment’s prior. The same is true for the posterior which is only logically after the prior, not causally, for example I could reason that since I know your house was burned down when I checked today (prior) then your house probably was also burned down yesterday, here the information flows causally in the wrong direction.

There are 4 common ways to set priors: group invariance, maximum entropy, marginalization, and coding theory, where this book mostly focuses on the first two.

Since the 3 previous chapters have given us: logic, the product and sum rule and sampling theory. Jaynes trivially derives Bayes theorem and names it like we are used to:

$$P(H\mid DX)=P(H\mid X)\frac{P(D\mid HX)}{P(D\mid X)}$$

In common parlance these 4 probabilities (or distributions) are called:

• $P(H\mid X)$ is the prior information we have about the hypothesis before the data
• $P(D\mid HX)$ is the likelihood or sampling function which says how likely the data is under different hypotheses, in short: what does the hypothesis say about the data?
• $P(D\mid X)$ is the probability of the data, and is usually found by marginalization (iterating over all the hypothesis)
• $P(H\mid DX)$ is called the posterior, it contains the information we have after considering the prior and data.

So when you read Bayes theorem above, you should say:

$$posterior=prior\frac{likelihood}{data}$$

Note that Jaynes writes it as prior times likelihood and not likelihood times prior, as modern Bayesians do.

Bayesian Update

The simplest math in all of the book is introduced here in chapter 4. It is basically a log odds version of Bayes theorem, which is very cool, enables fast calculation and is useful for intuitions about updating beliefs, we will go through it here. If you hate math then skip to chapter 5.

First we write the posterior for a hypothesis H and not H (written $\overline{H}$)

$$P(H\mid DX)=\frac{P(D\mid HX)P(H\mid X)}{P(D\mid X)}$$

$$P(\overline{H}\mid DX)=\frac{P(D\mid \overline{H}X)P(\overline{H}\mid X)}{P(D\mid X)}$$

The relationship between odds and probability is that the odds is basically ‘it happened’ divided by ‘it didn’t happen’, so if something is 50/50 then we have 1:1 odds or $p/\overline{p}=0.5/0.5=1$, if we have 90% and 10% outcomes, then we have 9:1 odds or $0.9/0.1=9$. We can do the same with the two above posterior equations by dividing them with each other to get their odds.

$$\frac{P(H\mid DX)}{P(\overline{H}\mid DX)}=\frac{\frac{P(D\mid HX)P(H\mid X)}{P(D\mid X)}}{\frac{P(D\mid \overline{H}X)P(\overline{H}\mid X)}{P(D\mid X)}}$$

$$O(H\mid DX)=O(H\mid X)\frac{P(D\mid HX)}{P(D\mid \overline{H}X)}$$

The trick here is that both equations contain $P(D\mid X)$ which is the hardest to calculate, and that number drops out when we divide the equations. So now we have posterior odds is prior odds times the likelihood ratio of the data under the two hypotheses.

Jaynes now defines a evidence function as follows:

$$e(H\mid DX)=10{\log }_{10}O(H\mid DX)$$

This evidence function is used to ‘quickly’ do Bayesian updates, much like Eliezer has introduced the concept of 1 bit of evidence, which is the evidence needed to go from odds 1:1 to 1:2 odds, Jaynes here uses decibel (dB) like the ones we use for sound as his evidence scale, this means that 0 means 1:1 odds just like 0 bits of evidence means 1:1 odds, 10 means 1:10 and 20 means 1:100 (because 10*10=100), so every 10 dB of evidence increases the odds by a factor of 10, and every 3 dB of evidence increases the odds by about a factor of 2 (${10}^{.3}$ is ~1.99526), meaning that 13 dB of evidence is equivalent for 1:20 odds.

We can use this to get the evidence of the posterior:

$$e(H\mid DX)=10{\log }_{10}O(H\mid DX)$$

$$e(H\mid DX)=10{\log }_{10}\frac{P(H\mid DX)}{P(\overline{H}\mid DX)}$$

Now let us try to use this. Imagine the following background information $X$: There are 11 raiding parties potentially attacking our cities, and it is always the same raiding party attacking all cities.

• 10 are made of goblins who breach the walls with probability ⅙,
• 1 is made of stronger orcs who breach the walls with probability ⅓.

We now want to consider the hypothesis that we were attacked by orcs, the prior odds are 10:1, so $e(H\mid X)=-10$.

To see how we should update future data (inspecting the walls of attacked cities) let us write out all the possibilities:

$$P(\text{breached}\mid \text{orc},X)=\frac{1}{3},P(\text{intact}\mid \text{orc},X)=\frac{2}{3}$$

$$P(\text{breached}\mid \text{goblin},X)=\frac{1}{6},P(\text{intact}\mid \text{goblin},X)=\frac{5}{6}$$

We observe that the walls were breached, which constitutes:

$$10{\log }_{10}\left(\frac{1/3}{1/6}\right)=3dB$$

The cool thing about log evidence whether decibel or bits is that adding logs is the same as multiplying the original numbers, and since probabilities of multiple events is the product of all the probabilities, this corresponds to summing (adding) all the evidence. This means we can simply add the 3 to our initial evidence -10 to get posterior evidence -10+3=-7 that the orcs did it. The next day another city has been attacked but the walls still stand, this changes the evidence by:

$$10{\log }_{10}\left(\frac{2/3}{5/6}\right)\approx -1\text{dB}|$$

From this the king can quickly survey all the sacked cities, count the walls and get:

$$e(\text{orcs}\mid DX)=-10+3\text{walls destroyed}-1\text{walls intact}$$

There were 20 destroyed walls and 37 intact walls, leading to $-10+3\times 20-1\times 37=13dB$ of evidence for the orc hypothesis, corresponding to 20:1 odds that the orcs did it.

Chapter 5: Queer uses for probability theory

This is the cool chapter. The book has lots of sections like this, but mostly in the latter parts of the book as Jaynes is in the habit of building a strong statistical foundation before throwing shade at frequentists.

In chapter 5, Jaynes introduces four intriguing examples for applying probability theory that are much more practical than drawing balls from an urn. These are chosen to reveal counterintuitive notions and fallacies. A recurring theme is that when interpreting evidence, the null hypothesis should not be considered in a vacuum, and doing so can lead to disastrous results and strawman arguments. The alternative hypotheses must be considered as well.

ESP

How many times would someone claiming to have ESP have to be right to convince you that they had supernatural powers, and said they could repeatedly guess another person’s number from 1 to 10? Jaynes says even after 4 correct guesses in a row, he wouldn’t consider it, but maybe around 10 guesses he would entertain it, so his prior state of belief is below -40 dB and probably more like -100 dB. In the ESP experiment quoted, the person claiming to have ESP guessed correctly 9410 of 37100 trials (25%) for a guess that random chance would hit 20% of the time. Jaynes does the math to show the probability of this result due to random chance using the Bernoulli distribution is the fantastically low value of 3.15e-139.

If someone shows you an experiment that is 10 standard deviations away from the mean of the null hypothesis because the N is so large, should you suddenly start believing in ESP? Our intuition trained on Less Wrong, says ‘of course not’, which means we should slow down here and look at the aspects of the problem beyond the null hypothesis. You might accept this for toy problems like drawing balls from an urn, but in non theoretical problems like ESP, you use a complex model of the world, built from a lifetime of experience that considers many alternative explanations and weighs this evidence against all of them.

If we only consider two possible hypotheses, one where ESP doesn’t exist and any results are due to luck, and one where the person really has ESP, then each guess is +10 dB of evidence for ESP. But then Jaynes says, “In fact, if he guessed 1000 numbers correctly, I still would not believe that he has ESP”. This is because there are many other hypotheses to consider in the real world, including faulty experimentation, incorrect assumptions (e.g. the distribution of choices is not uniform), and deception, which also start with very low priors, but higher than the ESP prior, at around -60 dB. Any successful guess will boost the deception and faulty experiment hypothesis more than the ESP hypothesis so that it’s always some ~40 dB above it. Implicit in this is that Jaynes would need other types of evidence besides just repeated correct guesses from one experiment to bring the ESP hypothesis high enough to be plausible. This evidence would be the type of evidence that was against either the deception or the faulty experiment hypotheses.

Crows

The next interesting story Jaynes discusses is about the paradox of intuition in Hempel’s paradox: Consider the hypothesis “All crows are black.” What is evidence for this hypothesis? Is a black crow evidence for this hypothesis? Is a white shoe evidence for this, since “All crows are black” is logically equivalent to “All non-black things are non-crows”? And a white shoe is a good example of a non-black non-crow! As is often the case, the answer to what counts as evidence is ‘it depends’, but it depends on more than just the hypothesis that all crows are black. It depends on what alternative hypotheses are considered.

I.J. Good’s response (with the title ‘The white shoe is a red herring’) shows what happens if you observe a black crow and consider just two hypotheses:

• A world where crows are always black but rare (1/10000 birds are crows, 9999/10000 are parrots)
• Another world where there are only crows, but only 10% of them are black.

If these are your only hypotheses, seeing a black crow is 30 dB (1000:1) of evidence that you are in the second world where not all crows are black. This is because for every black crow in world one there are 1000 black and 10000 white crows in world two, thus a black crow is stronger evidence for world two.

If we modified the first world to one where crows are always black, and very common, then observing a black crow is evidence for the modified first world over the second.

This story provides an intuitive perspective on Jaynes’ ideas on multiple hypotheses, namely that whether or not a given piece of data is evidence for a hypothesis depends upon which hypotheses are being considered. One of the key takeaways from these stories is that the acknowledgement of hypotheses and the relationship of multiple hypotheses in a person’s mind determines how to interpret evidence and assign probabilities. Rationalists typically are aware that the probability of an event is not stored in the physical object being observed, but in the uncertainty in the observer’s mind about the object. In the black crow paradox, the feeling of paradox comes from a similar fallacy that the probabilities are stored in the individual hypotheses themselves instead of the uncertainty about all hypotheses as they relate to each other and the evidence.

Are Humans using Bayesian Reasoning?

Kahneman and Tversky (1972) and Wason and Johnson Laird (1972) both show that humans commit violations of Bayesian reasoning, the most extreme is the ‘A implies B’ which many people consider equivalent to ‘B implies A’ where the correct logical rule is ‘not B implies not A’. Jaynes argues this is an example of Bayesian reasoning. For example if all dogs are mammals (deduction) it also means that some mammals are dogs, concretely if only 20% of animals are mammals this information increased the likelihood of dogs by a factor of 5!. A implies B means that B increases the likelihood of A by a factor of 5.

Chapter 6: Elementary Parameter Estimation

This chapter would usually be chapter 1 or assumed reading of normal statistical books, alas, we are now on page 149 and Jaynes finally introduces the concept of a parameter! This is like writing a 149 pages introduction to programming without introducing the concept of a variable for “pedagogical reasons”. The pedagogical trick being played here is to save yourself from the mind projection fallacy. If your model (or computer program) has a parameter for the frequency of red balls being drawn from my basket then that is a feature of your model, not a feature of the basket! How can you write 150 pages of statistics without variables? Because they are not real! The way Jaynes pulled it off was by always pointing to the events in the world rather than the parameters in a statistical model in his head, so we have $p(R_3|R_1,R_2,X)$, the probability that the 3rd draw from the urn is a red ball given two previous red draws, rather than $p(\theta |R_1,R_2,X)$ where $\theta$ is the “urns propensity to produce red balls”. Thanks Jaynes!

First, we’ll introduce the maximum likelihood estimator (MLE), which can be used to estimate outcomes or parameters. This method can be applied once you are able to assign probabilities to every possible outcome, by literally selecting the outcome with the highest probability as your estimate. This effectively discards a lot of information about the distribution, and can produce counterintuitive results if the discarded information was actually useful. There are some cases where this will have ‘atypical’ estimates (that are outside of the ‘typical set’ in information theory). An easy to understand example is that if you have a 60/40 biased coin, the MLE for a 1000 sequence of flips will be 1000 heads in a row. Note that this all-heads result is the most likely estimate of the sequence, which we are focusing on to show counterintuitive properties of MLE (you could use MLE to estimate the number of total heads to expect instead of the ordered sequence, and it would estimate 600 heads here). In real life we’d always expect some tails in the sequence, and we’d expect more tails if the coin is closer to 50/50, but the MLE is indifferent to the degree of fairness that the coin has - for any even slightly biased coin it will be all heads. If you think about this further, MLE can be very blunt, since all coins probably have some tiny physical difference that would bias them just a teeny bit to one side of the coin (say 49.999999999% heads, 50.00000001% tails), so all MLE estimates for coin flip sequences should be all heads or all tails if we inspect them closely enough. This example is for the MLE of an outcome, given the coin’s bias parameter, which is arguably the easier case to grok. The other way to use it is to find the most likely estimate for the parameter (e.g. the amount of bias in the coin) given data (e.g. a sequence of coin flips).

Jaynes' very physicist-oriented example concerns the emission of particles from a radioactive source and a sensor that can detect some portion of these particles. The radioactive source emits on average $s$ particles per second drawn from a Poisson distribution and the sensor detects particles with an Bernoulli rate of $\varphi$. So if $\varphi$ is 0.1, the sensor picks up 10% of particles over the long run, but if you have just $n=10$ particles, there is no guarantee that it will detect exactly 1 particle. Similarly, even though we might have $s=100$ particles per second, any given second might have more or less than 100 particles emitted. This is where it gets complicated. If you use the MLE estimate, you will always get $\varphi s$ particles as your estimate for each second of counts, because MLE ‘assumes’ that the 10:1 particle relationship is fixed and thus ignores the Poisson source variability. So let’s say you have a counter with $\varphi =0.1$ and have observed a count of 15 particles on this sensor for some second. How many particles, $n$, have originated from the source during this second? MLE will get you 150 particles, as described above. But Jayne’s robot gives us 105 particles. What? This is a HUGE difference! This example also surprised experimental physicists. The reason the robot gets 105 and not 150 is because the source has lower variability than the detector, so a high number is weak evidence of an above average number of particles.

While the above may seem very counter intuitive, all the confusion can be fixed by plotting the above distribution (Which Jaynes does not do). Below we have 3 plots:

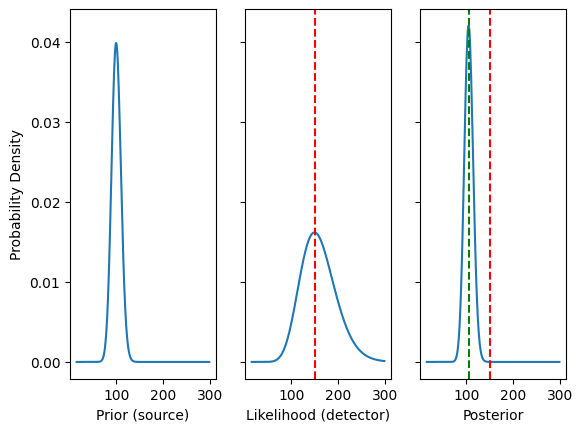
Where:

• The left is the source which follows a Poisson distribution: $s\sim Poisson(k=100)$
• The middle is the detector, which follows a Binomial distribution: $n\sim Binomial(c=15,\varphi =0.1)$
• The right is the posterior compromises of n between the prior (source) and likelihood (detector)
• The red line is the MLE estimate of 150, the green is the Bayesian estimate of 105.

It is very easy without fancy math to see that the prior is narrow and the likelihood is broad, so the posterior compromise should favor the prior, in modern parlance this approach is called “full Bayesian” because we use the full distributions to make inference, where the MLE approach hopes that the mode of the distributions capture sufficient information.

Back in math land: by using the Poisson distribution to model the distribution of particles given the source strength and sensor counts, and using the entire posterior distribution to calculate the expected number of originating particles, Jaynes’ robot takes the 15 observed particles as the minimum possible particles (we assume the sensor doesn’t produce counts without particles), and adds to this $100(1-0.1)=90$, where the 100 comes from $s$ and 0.1 comes from $\varphi$. As the coin example shows, MLE can be blunt, because it doesn’t consider all of the information - in the coin example it didn’t care about the degree of bias. In this particle/sensor example, MLE didn’t care about the source strength, $s$. (We should note that there is a risk of strawmanning MLE too much if we don’t mention there may be ways to ameliorate this with MLE by asking a different question, but the point is that incorporating more information can be good sometimes, and MLE often discards information). As non-physicists, we also feel Jaynes is also probably incorporating some physicist-internalized priors such as how to think about the standard deviation for particle radiation. Jaynes gives more detail:

“What caused the difference between the Bayes and maximum likelihood solutions? The difference is due to the fact that we had prior information contained in this source strength s. The maximum likelihood estimate simply maximized the probability for getting c counts, given n particles, and that yields 150. In Bayes’ solution, we will multiply this by a prior probability $p\left(n|s\right)$, which represents our knowledge of the antecedent situation, before maximizing, and we’ll get an entirely different value for the estimate. As we saw in the 6 Elementary parameter estimation 177 inversion of urn distributions, simple prior information can make a big change in the conclusions that we draw from a data set.”

Jaynes extends the particle sensor example in a very interesting way: where the information about the sensor is the same, but with different prior information (such as the source being allowed to change versus being fixed) to get different results. This all demonstrates the usefulness of the Bayesian principles of getting better estimates by incorporating more information, and accepting differences in estimates as differences in information.

Jaynes has a more advanced version of the problem where people enter and leave a radioactive room containing a source of unknown strength, and each person's radioactive exposure is measured with the same device with $\varphi =0.1$. In this example the first person's measured counts has weak evidence of the general source strength and therefore contains relevant information for inference of the second person's exposure.

Personal opinions

What the book achieves in 6 chapters is very impressive. From a philosophical perspective Jaynes derives the Bayesian framework from only logic and a few desiderata. Other Bayesians such as De Finetti come to many of the same conclusions easier using gambling and the principle of indifference. Jaynes personally finds gambling to be a very vulgar foundation for statistics. However, the important insight does not come from his aesthetic preference for logic, but that Jaynes's version of (Bayesian) statistics is grounded in information theory instead of gambling, and epistemologically it is much easier to ask the question “how does this information change my beliefs”, rather than: “If I was a betting man applying the principle of indifference to the outcomes, what odds would I then put on my prior beliefs so nobody can Dutch book me?” For simple problems Jaynes and De Finetti will invent the same priors and likelihoods, but for more advanced situations information theory gives a much better starting point for setting priors.

One of us works with proteomics (the study of all the proteins in the body), and saying “the effect of gender is large in some proteins, so it is probably also large on other proteins” (information theory), is actually how he thinks when he set up fancy hierarchical models with adaptive priors. He does not think “if I was a betting man and saw a large effect for gender for some proteins, then I would naturally use this adaptive weird prior so I do not lose money when betting with my coworkers”.

This is just the first quarter of the book, with a lot of detail removed. The spirit and foundation of the book is mostly captured in this first part. Some of the other sections are very mathy (e.g. properties of the Gaussian distribution and rants about why Jaynes thinks it should be called the central distribution instead), with significant focus on math and statistics history. As our example with proteomics illustrates, while this book is the book that has taught us the least per page about how to DO statistics, it is the one that has taught us the most about how to THINK about statistics. As the many examples in the book show, intuition in statistics and probability theory is something that must be built bottom-up from common sense and careful thinking about information and evidence, or else we risk getting it wrong by approaching data from the top-down, missing the structure of the underlying information.

Thanks to Mateusz Bagiński and the LW editor for their valuable feedback.