(Cross-posted from my blog)

So this paper by the trio from the FHI, Anders Sandberg, Eric Drexler and Toby Ord (SDO for short) has been talked about quite a bit, on LessWrong, on SSC and on Reddit. It is about how their Monte-Carlo calculations based on probability distributions rather than on the usual point estimates of the Drake equation apparently dissolves the question of why we are seemingly alone in the Universe that is supposed to be teeming with intelligent life, if one takes the Copernican idea "we are not special" seriously. One grim suggestion is that there is a Great Filter that is still in front of us and is almost guaranteed to kill us off before the human civilization reaches the technological levels observable by other civilizations like ours.

There are plenty of other ideas, most addressing various factors in the Drake equation, but the one advanced in SDO is quite different from the mainstream: they say that estimating these factors is a wrong way to go, because the uncertainty in these very small probabilities is so large, the point estimates are all but meaningless. Instead they suggest that the correct approach is something along the following lines: First, assume a reasonable probability distribution for each factor, then draw a value for each factor based on their probability distributions, calculate the resulting expected value of the number of currently detectable civilizations, then repeat this process many times to create a synthetic probability distribution of the number of this civilizations, and finally extract the odds of us being alone in the universe from this distribution. And that is what they did, and concluded that the odds of us being alone in the Milky Way are something like 1:3. Thus, according to SDO, there is no paradox, an average universe is naturally a desolate place.

Their to the Fermi paradox solution is basically

Due to random chance, some of the parameters in the Drake equation, we do not know which, we do not know why, are many orders of magnitude smaller in our universe than previously estimated.

I have an issue with calling it "dissolving the paradox", since it doesn't answer any of the practical questions about the universe we live in. Fermi's question, "Where is everybody?" remains open.

But I may have misunderstood the paper. So, what follows is an attempt to understand their logic by reproducing it. Here I will analyze their toy model, as it has all the salient features leading to their conclusion:

There are nine parameters (f1, f2, . . .) multiplied together to give the probability of ETI [Extra-terrestrial intelligence] arising at each star. Suppose that our true state of knowledge is that each parameter could lie anywhere in the interval [0, 0.2], with our uncertainty being uniform across this interval, and being uncorrelated between parameters.

A point estimate would be taking a mean for each factor and multiplying them, giving one-in-a-billion chance per star, which results in a virtual certainty of ETI at least somewhere in a galaxy of hundreds of billions of stars.

Let's try a distribution estimate instead: take 9 random numbers from a uniform distribution over the interval [0, 0.2]. Here is a bunch of sample runs, the expected values of ETIs in the toy galaxy, and the odds of the toy galaxy being empty:

Notice that, out of the 10 sample galaxies in this example, about half show considerable odds of being empty, highlighting the difference between using a distribution and the point estimates. SDO likely had run a lot more simulations to get more accuracy, and I did, too. Here is the distribution of the odds for a given number of ETIs in the galaxy, based on about ten million runs:

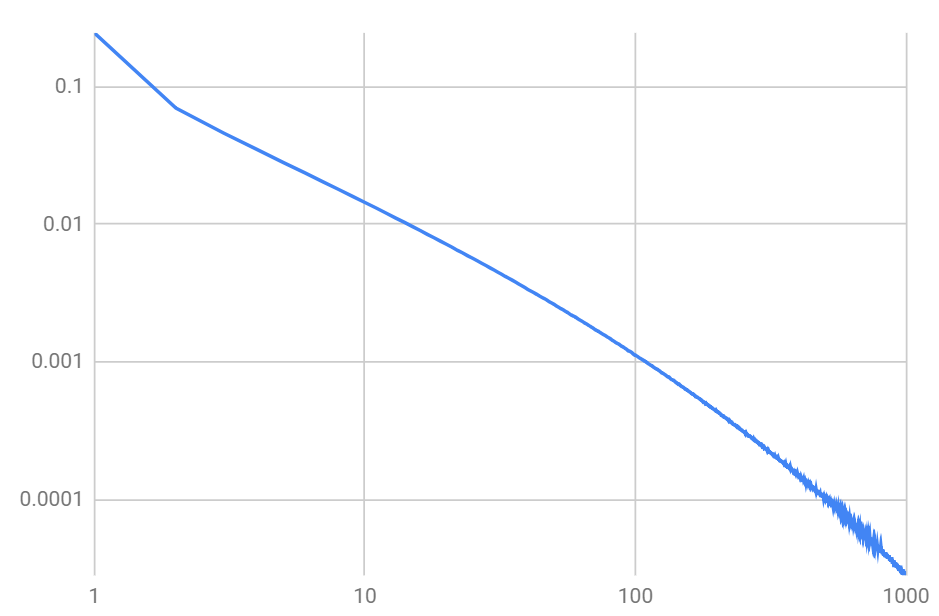
The horizontal axis is the number of ETIs, and the vertical axis is the probability of this number of ETIs to happen in a given toy galaxy drawn at random, given the probability distribution for each factor, as specified above.

Notice how wide this distribution is: some galaxies are completely bereft of ETIs, while others have hundreds and even thousands of them!

The above graph is very close to the power law: the probability of the number of ETIs goes roughly as the number of ETIs to the power of -1.2. This means that the estimate of the expected number of ETIs is actually divergent, though the median number of ETI's per galaxy is finite and about 30. So, somewhat paradoxically,

Using the distributional estimate instead of a point estimate both increases the likely number of ETIs per galaxy, and the fraction of empty galaxies.

The paper states that "Monte Carlo simulation shows that this actually produces an empty galaxy 21.45% of the time," but does not specify the way this number was calculated. From the plot above, the probability of having between zero and one ETIs, whatever it might mean, is 24.63%. A different way of calculating the average odds of an empty toy galaxy would be to calculate the odds of each sample galaxy to be empty as 

P(empty) = (1-p_1*p_2*...*p_9)^(10^11) 

then average all these odds. This approach gives the fraction of empty galaxies as 21.43%, very close to the number quoted in the paper. 

This toy example demonstrates nicely the main result of the SDO paper: the usual point estimate produces a wildly inaccurate expected fraction of galaxies with no ETIs in them. The rest of the SDO paper is focused on calculating a more realistic example, based on the current best guesses for the distributions of each factor in the Drake equation:

Using these distributions and their further refinements to calculate the odds yield the following conclusion:

When we update this prior in light of the Fermi observation, we find a
substantial probability that we are alone in our galaxy, and perhaps even in our
observable universe (53%–99.6% and 39%–85% respectively). ’Where are they?’
— probably extremely far away, and quite possibly beyond the cosmological
horizon and forever unreachable.

If our universe is drawn at random from the pool of factors with the distributions as suggested by the paper, then there are substantial odds that we are alone in the observable universe.

This is because some of the factors in the Drake equation, due to their uncertainty, can end up many orders of magnitude smaller than the value used for a point estimate, the one where this uncertainty is not taken into account. There is no claim which of the parameters are that small, since they differ for different desolate universes. Just the (bad) luck of the draw.

So, the Fermi paradox has been solved, right? Well, yes and no. Once we draw a set of parameters to use in the Drake equation in one specific universe, for example ours, we are still left with the task of explaining their values. We are no closer to understanding the Great Filter, if any, than before. Is abiogenesis extremely rare? Do ETIs self-destruct quickly? Are there some special circumstances required for life to thrive beyond the planet being in the Goldilocks zone? Is there the singleton effect where the first civilization out of the gate takes over the galaxy? Who knows. SDO concludes that 

This result dissolves the Fermi paradox, and in doing so removes any need to invoke speculative mechanisms by which civilizations would inevitably fail to have observable effects upon the universe.

I find that this conclusion does not follow from the main result of the paper. We live in this one universe, and we are stuck with the specific set of values of the factors in the Drake equation that our universe happened to have. It is quite possible that in our universe there is a Great Filter "by which civilizations would inevitably fail to have observable effects upon the universe," because, for example one specific parameter has the value that is many orders of magnitude lower than the estimate, and it would be really useful to know which one and why. The error SDO is making is looking at the distribution of the universes, whereas the Fermi paradox applies to the one we are stuck with. A real resolution of the paradox would be, for example, determining which parameters in the Drake equation are vanishingly low and why, not simply declaring that it is exceedingly likely that a randomly drawn universe has one or several vanishingly small parameters leading to it being very likely bereft of ETIs.