LESSWRONG
is fundraising!
LW
$

by Morendil
6 min read
83

20

This post summarizes response to the Less Wrong Book Club and Study Group proposal, floats a tentative virtual meetup schedule, and offers some mechanisms for keeping up to date with the group's work. We end with summaries of Chapter 1.

Statistics

The proposal for a LW book club and study group, initially focusing on E.T. Jaynes' Probability Theory: The Logic of Science (a.k.a. PT:TLOS), drew an impressive response with 57 declarations of intent to participate. (I may have missed some or misinterpreted as intending to participate some who were merely interested. This spreadsheet contains participant data and can be edited by anyone (under revision control). Please feel free to add, remove or change your information.) The group has people from no less than 11 different countries, in time zones ranging from GMT-7 to GMT+10.

Live discussion schedule and venues

Many participants have expressed an interest in having informal or chatty discussions over a less permanent medium than LW itself, which should probably be reserved for more careful observations. The schedule below is offered as a basis for further negotiation. You can edit the spreadsheet linked above with your preferred times, and by the next iteration if a different clustering emerges I will report on that.

  • Tuesdays at UTC 18:00 (that is 1pm Bay Area, 8pm in Europe, etc. - see linked schedule for more)
  • Wednesdays at UTC 11:00 (seems preferred by Australian participants)
  • Sundays at UTC 18:00 (some have requested a weekend meeting)

The unofficial Less Wrong IRC channel is the preferred venue. An experimental Google Wave has also been started which may be a useful adjunct, in particular as we come to need mathematical notations in our discussions.

I recommend reading the suggested material before attending live discussion sessions.

Objectives, math prerequisites

The intent of the group is to engage in "earnest study of the great literature in our area of interest" (to paraphrase from the Knowledge Hydrant pattern language, a useful resource for study groups).

Earnest study aims at understanding a work deeply. Probably (particularly so in the case of PT:TLOS) the most useful way to do so is sequentially, in the order the author presented their ideas. Therefore, we aim for a pace that allows participants to extract as much insight as possible from each piece of the work, before moving on to the next, which is assumed to build on it.

Exercises are useful stopping-points to check for understanding. When the text contains equations or proofs, reproducing the derivations or checking the calculations can also be a good way to ensure deep understanding.

PT:TLOS is (from personal experience) relatively accessible on rusty high school math (in particular requires little calculus) until at least partway through Chapter 6 (which is where I am at the moment). Just these few chapters contain many key insights about the Bayesian view of probability and are well worth the effort.

Format

My proposal for the format is as follows. I will post one new top-level post per chapter, so as to give people following through RSS a chance to catch updates. Each chapter, however, may require splitting up into more than one chunk to be manageable. I intend to aim for a weekly rhythm: the monday after the first chunk of a new chapter is posted, I will post the next chunk, and so on. If you're worried about missing an update, check the top-level post for the current chapter weekly on mondays.

Each update will identify the current chunk, and will link to a comment containing one or more "opening questions" to jump-start discussion.

Updates also briefly summarize the previous chunk and highlights of the discussion arising from it. (Participants in the live chat sessions are encouraged to designate one person to summarize the discussion and post the summary as a comment.) By the time a new chapter is to be opened, the previous post will contain a digest form of the group's collective take on the chapter just worked through. The cumulative effect will be a "Less Wrong's notes on PT:TLOS", useful in itself for newcomers.

Chapter 1: Plausible Reasoning

In this chapter Jaynes fleshes out a theme introduced in the preface: "Probability theory as extended logic".

Sections: Deductive and Plausible Reasoning - Analogies with Physical Theories - The Thinking Computer - Introducing the Robot (week of 14/06)

Classical (Aristotelian) logic - modus ponens, modus tollens - allows deduction (teasing apart the concepts of deduction, induction, abduction isn't trivial). But what if we're interested not just in "definitely true or false" but "is this plausible", as we are in the kind of everyday thinking Jaynes provides examples of? Plausible reasoning is a weaker form of inference than deduction, but one Jaynes argues plays an important role even in (say) mathematics.

Jaynes' aim is to construct a working model of our faculty of "common sense", in the same sense that the Wright brothers could form a working model of the faculty of flight, not by vague resort to analogy as in the Icarus myth, but by producing a machine embodying a precise understanding. (Jaynes, however, speaks favorably of analogical thinking: "Good mathematicians see analogies between theorems; great mathematicians seen analogies between analogies". He acknowledges that this line of argument itself stems from analogy with physics.)

Accordingly, Jaynes frames what is to follow as building an "inference robot". Jaynes notes, "the question of the reasoning process used by actual human brains is charged with emotion and grotesque misunderstandings", and so this frame will be helpful in keeping us focused on useful questions with observable consequences. It is tempting to also read a practical intent - just as robots can carry out specialized mechanical tasks on behalf of humans, so could an inference robot keep track of more details than our unaided common senses - we must however be careful not to project onto Jaynes some conception of a "Bayesian AI".

Sections: Boolean Algebra - Adequate Sets of Operations - The Basic Desiderata - Comments - Common Language vs Formal Logic - Nitpicking (week of 21/06)

Jaynes next introduces the familiar formal notation of Boolean algebra to represent truth-values of propositions, their conjunction and disjunction, and denial. (Equality denotes equality of truth-values, rather than equality of propositions.) Some care is required to distinguish common usage of terms such as "or", "implies", "if", etc. from their denotation in the Boolean algebra of truth-values. From the axioms of idempotence, commutativity, associativity, distributivity and duality, we can build up any number of more sophisticated consequences.

One such consequence, sketched out next, is that any function of n boolean variables can be expressed as a sum (logical OR) involving only conjunctions (logical AND) of each variable or its negation. Each of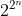 different logic functions can thus be expressed in terms of only 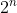building blocks and only three operations (conjunction, disjunction, negation). In fact an even smaller set of operations is adequate to construct all Boolean functions: it is possible to express all three in terms of the NAND (negation of AND) operation, for instance. (A key argument in Chapter 2 hinges on this reduction of logic functions to an "adequate set".)

The "inference robot", then, is to reason in terms of degrees of plausibility assigned to propositions: plausibility is a generalization of truth-value. We are generally concerned with "conditional probability"; how plausible something is given what else we know. This is represented in the familiar notation A|B (" the plausibility of A given that B is true", or "A given B"). The robot is assumed to be provided sensible, non-contradictory input.

Jaynes next considers the "basic desiderata" for such an extension. First, they should be real numbers. (This is motivated by an appeal to convenience of implementation; the Comments defend this in greater detail, and a more formal justification can be found in the Appendices.) By convention, greater plausibility will be represented with a greater number, and the robot's "sense of direction", that is, the consequences it draws from increases or decreases in the plausibility of the "givens", must conform to common sense. (This will play a key role in Chapter 2.) Finally, the robot is to be consistent and non-ideological: it must always draw the same conclusions from identical premises, it must not arbitrarily ignore information available to it, and it must represent equivalent states of knowledge by equivalent values of plausibility.

(The Comments section is well worth reading, as it introduces the Mind Projection Fallacy which LW readers who have gone through the Sequences should be familiar with.)

Personal Blog

20

Mentioned in
Book Club Update and Chapter 1
New Comment
83 comments, sorted by
top scoring
Click to highlight new comments since:
Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings
[-]taiyo60

Jaynes references Polya's books on the role of plausible reasoning in mathematical investigations. The three volumes are How to Solve it, and two volumes of Mathematics and Plausible Reasoning. They are all really fun and interesting books which kind of give a glimpse of the cognitive processes of a successful mathematician.

Particularly relevant to Jaynes' discussion of weak syllogisms and plausibility is a section of Vol. 2 of Mathematics and Plausible Reasoning which gives many other kinds of weak syllogisms. Things like: "A is analogous to B, B ... (read more)

Reply
[-]Risto_Saarelma50

Pdf link to Chapter 1.

Reply
1Maelin
Is there a PDF version that doesn't have the text looking faded and hard-to-read? Even zoomed in to page width on a 22" monitor it is not pleasant to look at. Or maybe there is some easy way to convert it (with all formatting intact) into a nicer looking font? I tried copy+pasting into Word but it appears to have not been properly OCRed and there are a lot of errors.
[-]xamdam140

try this

Here, actually: http://ifile.it/23ulwa7/0521592712.rar rar pwd: gigle.ws

Reply
0simplicio
Thanks, I concur, it's great!
0Maelin
Ah, that's great. Much nicer. Having the whole book in one PDF makes it easier for me too.
1[anonymous]
Looks fine to me in some PDF viewers (gv, foxit) and horribly aliased in others (evince, acrobat). I would guess it's a question of the quality of their scaling algorithms.
[-]arbimote40

EDIT: The original post now has updated times and links, so refer to that instead.

Here are links to the times suggested, for convenience:

I'd suggest posting meeting times using timeanddate.com, to help avoid confusion about time zones and daylight savings.

Reply
[-]Jonathan_Graehl40

From the preface:

We fail to present as many practical worked-out numerical examples as we should. Fortunately, three recent books largely make up this deficiency, and should be considered as adjuncts to the present work: Bayesian Spectrum Analysis and Parameter Estimation (Bretthorst, 1988), Maximum Entropy in Action (Buck and Macaulay, 1991), and Data Analysis – A Bayesian Tutorial (Sivia, 1996)

Which of these (or some other, more current, text) would you recommend?

Reply
[-]marc40

This might be of interest to people here; it's an example of a genuine confusion over probability that came up in a friends medical research today. It's not particularly complicated, but I guess it's nice to link these things to reality.

My friend is a medical doctor and, as part of a PhD, he is testing peoples sense of smell. He asked if I would take part in a preliminary experiment to help him get to grips with the experimental details.

At the start of the experiment, he places 20 compounds in front of you, 10 of which are type A and 10 of which are type B... (read more)

Reply
7Alicorn
Guess they're different every time. There are more pairs of different compounds from a selection group than pairs of same ones. (For any given compound, there are 9 matches and 10 non-matches.)
5simplicio
Probability that both compounds are A = P(1st is A)P(2nd is A) = (1/2)(9/19) = 0.24 Probability that both are B = 0.24 Probability that both are same = 0.47 Probability that they are different = 0.53 Conclusion: Always predict they are different.
2JoshuaZ
More detail in the protocol would be helpful. For example, do you get to repeatedly use the same bottle of the set? If so, I can do the following for a 20 trial set: Pick bottle 1. Now run through the other 19 bottles and guess for each that it is different from bottle 1. I'll be correct 10 out of 19 trials. This method generalizes in a fairly obvious fashion although it isn't clear to me if one is going to do n trials whether this is actually the optimal procedure for maximizing how often you are correct. I suspect that one can do better but it isn't clear to me how.
-1JoshuaZ
And can the person who downvoted this please explain why they did so?
0Morendil
This sounds like a great applied exercise for Chapter 3 on elementary sampling theory. ;)
[-][anonymous]30

I wish Lesswrong had an online book discussion section. How come we only analyze HPMoR in depth?

Reply
3gwern
Because only MoR is addictive enough to keep people reading and fannishly discussing it. There have been attempts to read/blog through many relevant texts like Jaynes or Dennett's Freedom Evolves, but inevitably, people lack the Conscientiousness to finish them. (There is a lesson here for academics: propaganda works.)
0[anonymous]
Perhaps MoR is addictive while other works are ... drier. So? What about the students who have to finish texts whether they like it or not because they are in an academic setting? What about the people that don't mind dry reading, as long as it is intellectual? I'm just saying that there should be an opportunity to do it, at least. I analyze scientific papers in journal clubs with other scientists. I enjoy it, because in the end you're gonna have a good discussion anyway.
0gwern
So‽ /looks around, sees no grades depending on people reading Jaynes & not quietly procrastinating on reading Jaynes Rara avis, indeed. Apparently there aren't many of you on LW, or else all the past attempts would do better... Synchronous discussions in person are quite different from asynchronous online attempts to do so.
[-]Torben30

In the spreadsheet, Finland has GMT +2. Does Finland not observe daylight savings time? I thought Finland wasn't in the CET zone? If I'm correct, Finland should be GMT +3

Reply
2Risto_Saarelma
There is a separate DST column for daylight saving time adjustment. 1 in the DST column means the time zone needs to be adjusted with daylight saving time
[-]Risto_Saarelma30

The meeting times should maybe be in UTC, the current ones are a bit confusing, since the city choice is a bit arbitrary. I don't even think the Paris and Melbourne times match, since Melbourne is currently on daylight saving time and Paris is not.

Reply
2Morendil
Oops.
3cwillu
I took the liberty of mucking up the spreadsheet a little bit: * Calculate preferred time in UTC * Sort names alphabetically * Total number of people who would prefer to have the meeting at a given UTC time. Once more people have filled in their preferred times, it might make sense to re-sort by that.
[-]Morendil30

Questions for the first part of Chapter 1:

  • Compare Jaynes' framing of probability theory with your previous conceptions of "probability". What are the differences?
  • What do you make of Jaynes' observation that plausible inference is concerned with logical connections, and must be carefully distinguished from physical causation?

(If you can think of other/better questions, please ask away!)

Reply
8Christian_Szegedy
Speaking of Chapter 1, it seems essential to point out another point that may be unclear on superficial reading. The author introduces the notion of a reasoning "robot" that maintains a consistent set of "plausibility" values (probabilities) according to a small set of rules. To a modern reader, it may make the impression that the author here suggests some practical algorithm or implementation of some artificial intelligence that uses Bayesian inference as a reasoning process. I think, this misses the point completely. First: it is clear that maintaining such a system of probability values even for a set of simply Boolean formulas (consistently!) amounts to solving SAT problems and therefore computationally infeasible in general. Rather, the author's purpose of introducing the "robot" was to avoid the misconception that plausibility desiderata are some subjective, inaccurate notions that depend on some hidden features of the human mind. So by detaching the inference rule from the human mind and using a idealized "robot", the author wants to argue that these axioms and their consequences can and should be studied mathematically and independently from all other features and aspects of human thinking and rationality. So here the objective was not to build some intelligence, rather study an abstract and computationally unconstrained version of intelligence obeying the above principles alone. Such an AI will never be realized in practice (due to inherent complexity limitations, and here I don't just speak about P!=NP !), Still, if we can prove what this theoretical AI will have to do in certain specific situations, then we can learn important lessons about the above principles, or even guide our decisions by that insights we gained from that study.
2xamdam
I agree that Jaynes is using the robot as a literary device to get a point across. If I understood you correctly it seems you're sneaking an additional claim that a Bayesian AI is theoretically impossible due to computational concerns. That should be discussed separately, but the obvious counterargument is that while, say, complete inference in Bayes Nets has been proved intractable, approximate inference does well on good-size problems, and approximate does not mean it's not Bayesian.
2Christian_Szegedy
Sorry, I never tried to imply that an AI built on the Bayesian principles is impossible or even a bad idea. (Probably, using Bayesian inference is a fundamentally good idea.) I just tried to point out that easy looking principles don't necessarily translate to practical implementations in a straightforward manner.
0Morendil
What then do you make of Jayne's observation in the Comments: "Our present model of the robot is quite literally real, because today it is almost universally true that any nontrivial probability evaluation is performed by a computer"?
0Christian_Szegedy
In my reading it means, that there are already actual implementations for all probability inference operations that the authors consider in the book. This has been probably a true statement, even in the 60'ies. It does not mean that the robot as a whole is resource-wise feasible. An analogy: It is not hard to implement all (non-probabilistic) logical derivation rules. It is also straightforward to use them to generate all true mathematical theorems (e.g. within ZFC). However this does not imply that we have an practical (i.e. efficient) general purpose mathematical theorem-prover. It gives an algorithm to prove every provable theorems eventually, but its run-time consumption makes this approach practically useless.
0Jonathan_Graehl
I assume you mean in the sense that deciding satisfiability of arbitrary propositions (over uncertain variables; certainly true/false ones can be simplified out) is NP-complete. Of course I mean that a variable v is uncertain if 0<p(v)<1.
0Christian_Szegedy
Actually, solving SAT problems is just the simplest case. Even so, if you have only certain variables (with either 0 or 1 plausibility), it's still NP-complete, you can't just simplify them in polynomial time. [EDIT: This is wrong as Jonathan pointed it out.] In extreme case, since we also have the rule that "robot" has to use all the available information to the fullest extent, it means that the "robot" must be insanely powerful. For example if the calculation of some plausibility value depends for example the correctness of an algorithm (known by the "robot", with a very high probability), then it will have to be able to solve the halting problem in general. Even if you constrain your probability values to be never certain or impossible, you can always chose small (or large) enough values, so that the computation of the probabilities can be used to solve the discrete version of the problem. For example, in the simplest case: if you just have a set of propositions in (let us say in conjunctive normal form), the consistency desideratum implies the ability of the "robot" to solve SAT problems, even if the starting plausibility values for the literals fall into the open (0,1) interval.
0Jonathan_Graehl
I think you misunderstood. The robot has a real number p(v) for every v. Let's grant an absolute min and max of 0 and 1. My point was simply that when p(v)=0 or p(v)=1, v can be simplified out of propositions using it. I understand why computing the probability of a proposition implies answering whether it's satisfiable.
1Christian_Szegedy
Sorry for the confusion. I was very superficial. Of course, your are correct about being able to simplify out those values.
4Zachary_Kurtz
I never thought about the connection between logic and probability before, though now it seems obvious. I've read a few introductory logic texts and deductive reasoning always seemed a bit pointless to me (in RL premises are usually inferred from something). - To draw from a literary example, Sherlock Holmes use of the phrase "deduce" always seemed a bit deceptive. You can say "that color of dirt exists only in spot x in London. Therefore, that Londoner must have come in contact with spot x if I see that dirt on his trouser knee." This is presented as a deduction, but really, the premises are induced and he assumes some things about how people travel. It seems more likely that we make inferences, not deductions, but convince ourselves that the premises must be true, without bothering to put real information about likelihood into the reasoning. An induction is still a logical statement, but I like the idea of using probability to quantify it.
5Jayson_Virissimo
As far as I can tell, Holmes actually engages in, what Charles Sanders Peirce called, "abduction". It is neither deduction nor induction.
0AlephNeil
I agree that Holmes is neither deducing nor "inducing", but I don't like this concept of "abductive inference". It's obvious that what we're after is the best explanation of the data we've collected, so it's never wrong to attempt to find the best explanation, but as advice, or as a description of how a rational agent proceeds, it's as useless as the advice to win a game of football by scoring more goals than the opposing side.
6JenniferRM
Perhaps yes... but... I have found over time that paying attention to interesting but weird features of a domain leads interesting places. The tractability problems inherent to some computational models of bayesian reasoning makes me suspect that "something else" is being used as "the best that can be physically realized for now" to do whatever it is that brains do. When evolutionary processes produce a result it generally utilizes principles that are shockingly beautiful and simple once you see them. I had not previously heard of the term "abductive reasoning" but catching terms like this is one of the reasons I love this community. The term appears to connect with something I was in a discussion about called "cogent confabulation". (Thanks for the heads up, Jayson!) The obvious thing that jumps out is that what Hecht-Neilson called "cogency" is strikingly similar to both Jayne's police example and the example of Sherlock Holmes. I'm tempted to speculate that the same "architectural quirk" in human brains that supports this (whatever it turns out to be) may also be responsible (on the downside) for both the Prosecutor's Fallacy and our notoriously crappy performance with Modus Tollens. Given the inferential distance between me and the many handed horror, this makes me think there is something clever to be said for whatever that quirk turns out to be. Maybe storing your "cause given evidence" conditional probabilities and your causal base rates all packed into a single number is useful for some reason? If I were to abduct a reason, it would be managing "salience" when trying to implement a practically focused behavior generating system that has historically been strongly resource limited. Its just a guess until I see evidence one way or the other... but that would be my "working hunch" until then :-)
3taiyo
Along with the distinction between causal and logical connections, when considering the conditional premise of the syllogisms (if A then B), Jaynes warns us to distinguish between those conditional statements of a purely formal character (the material conditional ) and those which assert a logical connection. It seems to me that the weak syllogisms only "do work" when the conditional premise is true due to a logical connection between antecedent and consequent. If no such connection exists, or rather, if our mind cannot establish such a connection, then the plausibility of the antecedent doesn't change upon learning the consequent. For example, "if the garbage can is green then frogs are amphibians" is true since frogs are amphibians, but this fact about frogs does not increase (or decrease) the probability that the garbage can is green since presumably, most of us don't see a connection between the two propositions. At some point in learning logic, I think I kind of lost touch with the common language use of conditionals as asserting connections. I like that Jaynes reminds us of the distinction.
2Craig_Heldreth
His example of the rain at 10:30 implying clouds at 10:15 with any physical causation going in the other direction is clear. And I appreciate his polemic that limiting yourself to reasoning based upon physical cause and effect is dull and impractical. He was a physicist and the ideal of physicists is to discover previously unknown natural laws of cause and effect, which made him a bit eccentric within his own community and so we get the tone in there of pleading. It is a minor distraction in the midst of great material. 57 participants should make for a sustained critical mass even with heavy attrition.
2cata
It occurs to me that Jaynes is missing a desideratum that I might have included. I can't decide if it's completely trivial, or if perhaps it's covered implicitly in his consistency rule 3c; I expect it will become clear as the discussion becomes more formal -- and of course, he did promise that the rules given would turn out to be sufficient. To wit: * The robot should not assign plausibilities arbitrarily. If the robot has plausibilities for propositions A and B such that the plausibility of A is independent of the plausibility of B, and the plausibility of A is updated, then the degree of plausibility for B should remain constant barring other updates. One more thing. The footnote on page 12 wonders: Does it follow that AND and NOT (or NAND alone) are sufficient to write any computer program? Isn't this trivial? Since AND and NOT can together be composed to represent any logic function, and a logic function can be interpreted as a function from some number of bits (the truth values of the variable propositions) to one result bit, it follows that we can write programs with AND and NOT that make any bits in our computer an arbitrary function of any of the other bits. Is there some complication I'm missing? (Edited slightly for clarity.)
6ata
You can use NAND to implement any algorithm that has a finite upper time bound, but not "any computer program", since a logical formula can't express recursion.
0[anonymous]
Does that mean that digital-eletronic NANDs which could be used to build flip-flops, registers, etc. cannot be expressed in a logical formula?
2pengvado
Electronic NAND gates have a nonzero time delay. This allows you to connect them in cyclic graphs to implement loops. You can model such a circuit using a set of logical fomulae that has one logical NAND per gate per timestep. Ata pointed out that you need an infinitely large set of logical formulae if you want to model an arbitrarily long computation this way. Though you can compress it back down to a finite description if you're willing to extend the notation a bit, so you might not consider that a problem.
0cata
I agree that you are correct. Thank you.
2Morendil
Not sure I see what you mean. Do you have an example?
2cata
I think I was unclear. Here's what I mean: Suppose our robot takes these two propositions: A = "It's going to rain tonight in Michigan." B = "England will win the World Cup." And suppose it thinks that the plausibility of A is 40, and the plausibility of B is 25. As far as our robot knows, these propositions are not related. That is, in Jaynes' notation (I'll use a bang for "not,") (A|B) = (A|!B) = 40, and (B|A) = (B|!A) = 25. Is that correct? Now suppose that the plausibility of A jumps to 80, because it's looking very cloudy this afternoon. I suggest that the plausibility of B should remain unchanged. I'm not sure whether the current set of rules is sufficient to ensure that, although I suspect it is. I think it might be impossible to come up with a consistent system breaking this rule that still obeys the (3c) "consistency over equivalent problems" rule.
3Morendil
If you know from the outset that these propositions are unrelated, you already know something quite important about the logical structure of the world that these propositions describe. Jaynes comes back to this point over and over again, and it's also a major theme of the early chapters in Pearl's Causality: -- Pearl, Causality p. 25
1magfrump
The way that you phrase this, "suppose the plausibility of A jumps to 80," has no rigor. Depending on the way you choose to calculate this, it could lead to change in B or not. if we consider them independent, we could imagine 100 different worlds, and we would expect in 40 of these worlds A to be true, etc., which would leave us with: 10 worlds where AB is true 30 worlds where A(!B) is true 15 worlds where (!A)B is true 45 worlds where (!A)(!B) is true In general I would expect evidence to come in the form of determining that we are not in a certain world. If we determine that the probability of A rises, because we know ourselves not to be in any world where (!A)(!B) is true, then we would have to adjust the probability of B. Your given reason, "because it's looking very cloudy this afternoon." Would probably indicate that we are uniformly less likely to be in any given world where A is false. In this case, the plausibility of A should jump without effecting the plausibility of B. So what I'm really saying is that there is no sense in which statements are independent, only a sense in which evidence is independent of statements. However, a lot of this is speculation since it really isn't addressed directly in the first chapter, as Christian points out.
1Christian_Szegedy
I think it is impossible to decide this based on Chapter 1 alone, for the second criterion (qualitative correspondence with common sense) is not yet specified formally. If you look into Chapter 2, the derivation of the product rule, he uses this rubber-assumption to get the results he aims for (very similarly to you). I think one should not take some statements of the author like ("... our search for desiderata is at an end... ") too seriously. In some sense this informative approach is defensible, from another perspective it definitely looks quite pretentious.
0[anonymous]
I don't understand what you mean by "(B|A) = (B|A')".
1simplicio
Probability is a 1-to-1 mapping of plausibilities onto real numbers, as opposed to an objective thing waiting to be discovered, mind-independently. It seems quite reasonable. His storm cloud analogy works quite well. I was particularly impressed with the "Comments" section after the chapter.
[-]Risto_Saarelma20

The study group pattern language link is great, by the way.

Reply
[-]Morendil10

Book Club Update

As promised, this is a "minor" update, i.e. I'm not making a new top-level post to prompt new reading for this week, but sticking to a comment. We have new information on meeting times, and new chunks to read. Next week we will start on Chapter 2, this time with a top-level update. We'll see how this works.

New live meeting schedule

The spreadsheet has proven effective as a way to coordinate meeting times for widely scattered participants starting from suboptimal initial values. The most voted-on time is UTC+18 which is around 1pm i... (read more)

Reply
4kmccarty
I find desideratum 1) to be poorly motivated, and a bit problematic. This is urged upon us in Chapter 1 mainly by considerations of convenience: a reasoning robot can't calculate without numbers. But just because a calculator can't calculate without numbers doesn't seem a sufficient justification to assume those numbers exist, i.e., that a full and coherent mapping from statements to plausibilities exists. This doesn't seem the kind of thing we can assume is possible, it's the kind of thing we need to investigate to see if it's possible. This of course will depend on what class of statements we'll allow into our language. I can see two ways forward on this: 1) we can assume that we have language of statements for which desideratum 1) is true. But then we need to understand what restrictions we've placed on the kinds of statements that can have numerical plausibilities. Or 2) We can pick a language that we want to use to talk about the world, and then investigate whether desideratum 1) can be satisfied by that language. I don't see that this issue is touched on in Chapter 1. There is further discussion of this in Appendix C; will this be discussed in connection with Chapter 1, or at some later time in the sequence? For example, in Appendix C, it turns out that desideratum 1 subdivides into two other axioms: transitivity, and universal comparability. The first one makes sense, but the second one doesn't seem as compelling to me.
0sophist
It is indeed an extremely interesting question! Perhaps it would be wiser to use complex numbers for instance. But intuitively it seems very likely that if you tell me two different propositions, that I can say either that one is more likely than the other, or that they are the same. Are there any special cases where one has to answer "the probabilities are uncomparable" that makes you doubt that it is so?
3kmccarty
Perhaps it might be wiser to use measures (distributions), or measures on spaces of measures, or iterate that construction indefinitely. (The concept of hyperpriors seems to go in this direction, for example.) Consider the following propositions. P1: The recently minted U.S. quarter I just vigorously flipped into the air landed heads on the floor. P2: A ball pulled from an unspecified urn containing an unspecified number of balls is white. P3(x): The probability of P2 is x Part of the problem is the laxness in specifying the language, as I mentioned. For example, if the language we use is rich enough to support self-referring interpretations, then it may not even be possible to coherently assign a truth value--or any other probability, or to know whether that is possible. But even ruling out Goedelian potholes in the landscape and uncountably infinite families of propositions, the contrast between P1 and P2 is problematic. P1 is backed up by a vast trove of background knowledge and evidence, and our confidence in asserting Prob(P1) = 1/2 is very strong. On the other hand, background knowledge and evidence about P2 is virtually nil. It is reasonable as a matter of customary usage to assume the number of balls in the urn is finite, and thus the probability of P1 is a rational number, but until you start adding in more assumptions and evidence, one's confidence in Prob(P2) < x for any particular real number x seems typically to be very much lower than for P1. Summarizing one's state of knowledge about these two propositions onto the same scale of reals between 0 and 1 seems to ignore an awful lot that we know about the relative state of knowledge vs. ignorance with respect to P1 and P2. An awful lot of knowledge is being jettisoned because it won't fit into this scheme of definite real numbers. To make the claim Prob(P2) = 1/2 (or any other definite real number you want to name) just does not seem like the same kind of thing as the claim Prob(P1) = 1/2. It feels
1Morendil
We're getting ahead of the reading, but there's a key distinction between the plausibility of a single proposition (i.e. a probability) and the plausibilities of a whole family of related plausibilities (i.e. a probability distribution). Our state of knowledge about the coin is such that if we assessed probabilities for the class of propositions, "This coin has a bias X", where X ranged from 0 (always heads) to 1 (always tails) we would find our prior distribution a sharp spike centered on 1/2. That, technically, is what we mean by "confidence", and formally we will be using things like the variance of the distribution.
1kmccarty
Ok, that sounds helpful. But then my question is this-- if we have whole family of mutually exclusive propositions, with varying real numbers for plausibilities, about the plausibility of one particular proposition, then the assumption that that one proposition can have one specific real number as its plausibility is cast in doubt. I don't yet see how we can have all those plausibility assignments in a coherent whole. But I'm happy to leave my question on the table if we'll come to that part later.
0pengvado
If you have a mutually exclusive and exhaustive set of propositions , each of which specifies a plausibility ) for the one proposition B you're interested in, then your total plausilibity is =\sum_iP(B|A_i)P(A_i)). (Actually this is true whether or not the A's say anything about B. But if they do, then this can be useful way to think about P(B).) I haven't said how to assign plausibilities to the A's (quick, what's the plausibility that an unspecified urn contains one white and three cyan balls?), but this at least should describe how it fits together once you've answered those subproblems.
0sophist
Very interesting! But I have to read up on the Appendix A4 I think to fully appreciate it...I will come back if I change my mind after it! :-) My own, current, thoughts are like this: I would bet on the ball being white up to some ratio...if my bet was $1 and I could win $100 I would do it for instance. The probability is simply the border case where ratio between losing and winning is such that I might as well bet or not do it. Betting $50 I would certainly not do. So I would estimate the probability to be somewhere between 1 and 50%...and somewhere there is one and only one border case in between, but my human brain has difficulty thinking in such terms... The same thing goes for the coin-flip, there is some ratio where it is rational to bet or not to.
-2[anonymous]
B°„bd‹¨È2«Î,¼·îðe8&"¯¯åØûÑ‹¥Õ»ãæLŒß¿~—ãmMvñ $0˜ÅÚ‡í­xf½wœçYÍØ9çG’•ÿñ8ʱ'|x‡P z‰ :kb\ȃiÉû2ÔA2i‘Õ„Ó4‘·DÅ™™ aèá;ºyÖ´òdÄPX‡å²ï<ã§[µaŠ¡îbˆ˜æ‰èbaÅÞï_,¶e©U9ê,H^»þ*¾
2taiyo
In formal logic, the disjunction "or" is inclusive -- "A or B" is true if A and B are true. In everyday language, typically "or" is exclusive -- "A or B" is meant to exclude the possibility that A and B are both true.
[-]magfrump10

I was on the LessWrong IRC just after 1pm PST (PDT? Whatever time my clock is set for, which should be the same as in San Francisco) and stayed there for about an hour, but no one was there discussing the book.

Does this time not work for people in the area? Or did people not expect to start the live discussions until next week? Did people in different areas have similar or different experiences to this?

Reply
1Risto_Saarelma
People haven't had extensive live discussions yet. I think we're currently collecting preferred times on the Google Docs spreadsheet and will decide on the weekdays and times of day when we've gotten more of those.
0magfrump
That answers my questions pretty well then.
[-]Larks00

In the section on 'Common Language vs Formal Logic', he mentions the two propositions

  • The room is noisy
  • There is noise in the room

and says the former is epistemological while the latter is ontological. Can anyone explain why this how this is the case? I can't make out the distinction at all, and infact parse the former as the latter.

Reply
0mattnewport
I'd guess that what he's getting at is that the first statement is merely reporting an observation while the second is making a claim about the state of the world and the entities within it. Of course such claims are somewhat implicit in the first to the extent that they are implicit in language but it is mainly reporting observations without explicitly tying them to claims about the world. The second statement is more explicitly calling out the existence of a thing called noise and a thing called a room and saying that the latter contains the former.
[-]patrickmclaren00

Is the study group still going ahead?

Reply
0Morendil
Yes, see the latest post - it hasn't been promoted (yet?), so if you're only getting the front page RSS feed you might have missed it.
[-]xamdam00

Thanks for point out the Pattern paper. I used to be a member of the group pictured on page 11 (NYC design patterns study group), recognize some of the faces ;)

Reply
[-][anonymous]00

Can someone a little more fluent in boolean algebra post the transformation that gets you from (1-8) to (1-9) (pg 107-108 in the pdf)? I haven't been able to work it out.

Reply
3Zachary_Kurtz
A different question about 1-8. I was able to figure out how he got A!B = !B (where ! is bar) but using the Boolean identities he provides, I couldn't get to B!A = !A. Can anyone enlighten me on this?
3red75
It seems we have just one rule to eliminate variables: substitution. For example, given A=BC and BCD=E, we can eliminate BC by substituting A for BC in BCD=E. Thus, we must have equation !A=X to get to B!A=!A, and to get to !A=X we must have !A=Y, and so on. So it seems impossible in given axiomatic system to derive B!A=!A from !B=AD. Am I missing something? EDIT: Here I take axioms in 1.12 as a basis for proposition calculus and I don't use any interpretation of them.
1arbimote
Perhaps what is missing is these rules: AT = A (1) AF = F (2) A + T = T (3) A + F = A (4) Which can be derived from the given axioms, apparently. I'm not sure if some necessary axioms were omitted. Using some of these, here's one way to derive B!A=!A from !B=AD: !B = AD !B + A = AD + A !B + A = AD + AT (1) !B + A = A(D + T) (Distributivity) !B + A = AT (3) !B + A = A (1) !!B!A = !A (Duality) B!A = !A
1nhamann
I think you just have to prove by truth table that P = P + PQ for any P, Q. Then we have: A = A + AD = A + !B => !A = !A !!B = !A B Second equation is by truth table, third is by definition. The equation after the implication is by DeMorgan's law (Jaynes calls it "duality") and the last is by double negation.
1red75
True+X=True and (True X)=X do follow from textual description of conjuction and dusjunction, but text before 1.13 suggests (misleads?) that B!A=!A can be derived by using axioms 1.12 only. Latter seems impossible.
1nhamann
Apologies, I totally edited out that part of my comment after finding a much simpler proof. I think my new derivation is fine assuming that proof by truth table is valid (which should be uncontroversial given that he uses it soon after this to show that AND and NOT are an "adequate set" for representing every logic function). Edit: I was not thinking clearly above. Of course proof by truth table is valid, because truth tables are the basis of the notion of logical equality, and Jayne's axioms don't make sense unless you accept that notion as a given.
0red75
Actually, you were thinking clearly. We can interpret 1.12 as axioms of proposition calculus, in a strange form of course. As I've done partly because of not very rigorous narration.
0Morendil
I think that's a truly excellent question, BTW. (If someone has an authoritative answer it should probably be ROT13'd.)
0Zachary_Kurtz
PS - in the free pdf it's 1-8. In the book the problem seems to have been renumbered to 1.13
1Morendil
I'm not sure there is a transformation intended... Proposition (1-9) appears by itself in a section that discusses "implication" (it introduces => as a shorthand for A=AB) and does not appear to follow from (1-8).
0[anonymous]
Hrm, no wonder it didn't work out. Thanks.
Moderation Log
83Comments