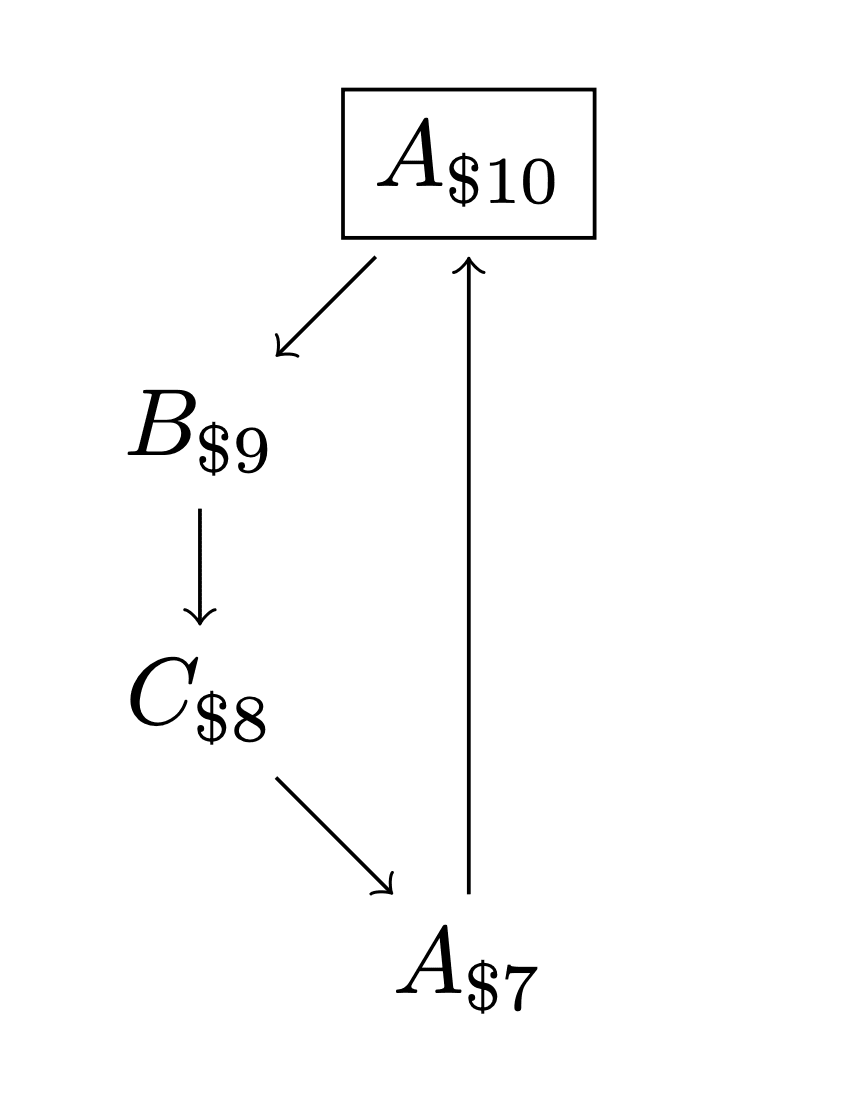
a confusion about preference orderings
13fbacus
6nostalgebraist
3fbacus
3cubefox
2Vladimir_Nesov
2cubefox
4Vladimir_Nesov
3cubefox
2Vladimir_Nesov
2cubefox
2Vladimir_Nesov
3Vladimir_Nesov
1fbacus
8Steven Byrnes
7clone of saturn
7Richard_Kennaway
8Elliott Thornley (EJT)
7Cole Wyeth
6cubefox
6Richard_Kennaway
6Dalmert
4Dagon
4Ape in the coat
4Veedrac
4XelaP
6Charlie Steiner
2Donald Hobson
2cubefox
2jmh
2SorenJ
4nostalgebraist
2Vladimir_Nesov
2cubefox
1martinkunev
1MinusGix
1Ivilivilly
1BryceStansfield
-1Samuel Hapák
-1Jonas Hallgren
New Comment
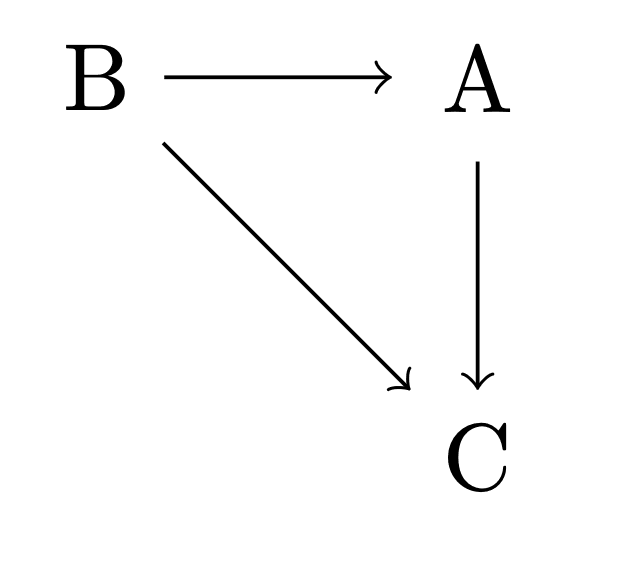
As Richard Kennaway noted, it seems considerations about time are muddling things here. If we wanted to be super proper, then preferences should have as objects maximally specific ways the world could be, including the whole history and future of the universe, down to the last detail. Decision theory involving anything more coarse-grained than that is just a useful approximation--e.g. I might have a decision problem with only two outcomes being "You get $10" and "You lose $5," but we would just be pretending these are the only two ways the world can end up for practical purposes, which is a permissible simplification since in my actual circumstances my desire to have more money over less is independent of other considerations. In particular the objects of preference are not states of the world at a time, since it is not a rational requirement that just because I prefer that one state instead of another obtain at I must also prefer likewise for . So, our agent who is perfectly content with their eternal A-B-C cycle is just one who likes this strange history of the world they can bring about, who nevertheless has potentially acyclic preferences. Indeed, this agent is still rational on orthodox decision theory even if they're paying for every such cycle. Similarly, in your case of the agent who goes through to get to , we would want to model the objects of preference as things like "Stay in the state indefinitely" and "Be in a -state for a little while and then be in a -state," and we would not want , , and themselves to be the objects of preference.
So what does this say about the money-pump argument for acyclicality, which seems to treat preferences as over states-at-a-time? I think the sorts of considerations you raise do show that such arguments don't go through unless we make certain (perhaps realistic) assumptions about the structure of agents' preferences, assuming we view the force of the money-pump arguments to come from the possibility of actual exploitation (some proponents don't care so much about actual exploitability, but think the hypothetical exploitability is indicative of an underlying rational inconsistency). For example, if I have the preferences , the argument assumes that there is some slightly worse version of that I still prefer to , that my preferences are coarse-grained enough that we can speak of my "trading" one of these states of affairs for another, that they are coarse-grained enough that my past trades don't influence whether I now prefer to trade for the slightly worse version of , and so on. If the relevant assumptions are met, then the money-pump argument shows that my cyclic preferences leave me with an outcome that I really will disprefer to having just stuck with , as opposed to ending up in a state I will later pay to transition out of (which is no fault of my rationality). You're right to point out that these really are substantive assumptions.
So, in sum: I think (i) the formalism for decision theory is alright in not taking into account the possibility of transitions between outcomes, and only taking into account preferences between outcomes and which outcomes you can affect in a given decision problem; and (ii) formalism aside, your observations do show limitations to/assumptions behind the money-pump arguments insofar as those arguments are supposed to be merely pragmatic. I do not know the extent to which I disagree with you, but I hope this clarifies things.
Thank you, this is thoughtful and interesting.
If we wanted to be super proper, then preferences should have as objects maximally specific ways the world could be, including the whole history and future of the universe, down to the last detail.
[...] it is not a rational requirement that just because I prefer that one state instead of another obtain at I must also prefer likewise for .
As you note, you're not the first commenter here to make these claims. But I just... really don't buy it?
The main reason is that if you take this view, several famous and popular arguments in decision theory become complete nonsense. The two cases that come to mind immediately are money pumps for non-transitive preferences and diachronic Dutch books. In both cases, the argument assumes an agent that makes multiple successive decisions on the basis of preferences which we assume do not vary with time (or which only vary with time in some specified manner, rather than being totally unconstrained as your proposal would have it).
If sequential decisions like this were simply not the object of study in decision theory, then everyone would immediately reject these arguments by saying "you've misunderstood the terminology, you're making a category error, this is just not what the theory is about." Indeed, in this case, the arguments probably would not have ever been put forth in the first place. But in reality, these are famous and well-regarded arguments that many people take seriously.
So either there's a clear and consistent object of study which is not these "maximally specific histories"... or decision theorists are inconsistent / confused about what the object of study is, sometimes claiming it is "maximally specific histories" and sometimes claiming otherwise.
Separately, if the theory really is about "maximally specific histories," then the theory seems completely irrelevant to real decision-making. Outside of sci-fi or thought experiments, I will never face a "decision problem" in which both of the options are complete specifications of the way the rest of my life might go, all the way up to the moment I die.
And even if that were the sort of thing that could happen, I would find such a decision very hard to make, because I don't find myself in possession of immediately-accessible preferences about complete life-histories; the only way I could make the decision in practice would be to "calculate" my implicit preferences about the life-histories by aggregating over my preferences about all the individual events that happen within them at particular times, i.e. the kinds of preferences that I actually use to make real-life decisions, and which I "actually have" in the sense that I immediately feel a sense of preferring one thing to another when I compare the two options.
Relatedly, it seems like very little is really "rationally required" for preferences about "maximally specific histories," so the theory of them does not have much interesting content. We can't make pragmatic/prudential arguments like money pumps, nor can we fall back on some set of previously held intuitions about what rational decision-making is (because "rational decision-making" in practice always occurs over time and never involves these unnatural choices between complete histories). There's no clear reason to require the preferences to actually relate to the content of the histories in some "continuous" way; all the "physical" content of the histories, here, is bundled inside contentless labels like "A" and is thus invisible to the theory. I could have a totally nonsensical set of preferences that looks totally different at every moment in time, and yet at this level of resolution, there's nothing wrong with it (because we can't see the "moments" at this level, they're bundled inside objects like "A"). So while we can picture things this way if we feel like it, there's not much that's worth saying about this picture of things, nor is there much that it can tell us about reality. At this point we're basically just saying "there a set with some antisymmetric binary relation on it, and maybe we'll have an argument about whether the relation 'ought' to be transitive." There's no philosophy left here, only a bit of dull, trivial, and unmotivated mathematics.
Thanks for the reply!
So, in my experience it's common for decision theorists in philosophy to take preferences to be over possible worlds and probability distributions over such (the specification of which includes the past and future), and when coarse-graining they take outcomes to be sets of possible worlds. (What most philosophers do is, of course, irrelevant to the matter of how it's best to do things, but I just want to separate "my proposal" from what I (perhaps mistakenly) take to be common.) As you say, no agent remotely close to actual agents will have preferences where details down to the location of every particle in 10,000 BC make a difference, which is why we coarse-grain. But this fact doesn't mean that maximally-specific worlds or sets of such shouldn't be what are modeled as outcomes, as opposed to outcomes being ways the world can be at specific times (which I take to be your understanding of things; correct me if I'm wrong). Rather, it just means a lot of these possible worlds will end up getting the same utility because the agent is indifferent between them, and so we'll be able to treat them as the same outcome.
I worry I might be misunderstanding your point in the last few paragraphs, as I don't understand how having maximally-specific worlds as outcomes is counter to our commonsense thinking of decision-making. It is true I don't have a felt preference between "I get $100 and the universe was in state S five billion years ago" and "I get $100 and the universe was in state T five billion years ago," let alone anything more specific. But that is just to say I am indifferent--I weakly prefer either outcome to the other, and this fact is as intuitively accessible to me as the fact that I prefer getting $100 to getting $10. As far as I can tell, the only consequence of making things too fine-grained is that you include irrelevant details to which the agent is indifferent and you make the model needlessly unwieldy--not that it invokes a concept of preference divorced from actual decision-making.
Outside of sci-fi or thought experiments, I will never face a "decision problem" in which both of the options are complete specifications of the way the rest of my life might go, all the way up to the moment I die.
Every decision problem can be modeled as being between probability distributions over such histories, or over sets of such histories if we want to coarse-grain and ignore minute details to which the agent is indifferent. Now, of course, a real human never has precise probabilities associated with the most minute detail--but the same is true even if the outcomes are states-at-times, and even non-maximally-specific states-at-times. Idealizing that matter away seems to be something any model has to do, and I'm not seeing what problems are introduced specifically by taking outcomes to be histories instead of states-at-times.
The two cases that come to mind immediately are money pumps for non-transitive preferences and diachronic Dutch books. In both cases, the argument assumes an agent that makes multiple successive decisions on the basis of preferences which we assume do not vary with time (or which only vary with time in some specified manner, rather than being totally unconstrained as your proposal would have it).
But having outcomes be sets of maximally-specific world-histories doesn't prevent us from being able to model sequential decisions. All we need to do so is to assume that the agent can make choices at different times which make a difference as to whether a more-or-less preferred world-history will obtain. For example, say I have a time-dependence preference of preferring to wear a green shirt on weekends and a red shirt on weekdays, so I'm willing to pay $1 to trade shirts every Saturday and Monday. This would not make me a money-pump, rather I'm just someone who's willing to pay to keep their favorite shirt at the moment on. But allowing time-dependent preferences like this doesn't prevent money-pump and diachronic Dutch book arguments from ever going through, for I still prefer wearing a red shirt next Monday to wearing a green shirt then, if everything else about the world-history is kept the same. If I in addition prefer wearing a yellow shirt on a weekday to wearing a red one, but then also prefer a green shirt on a weekday to a yellow one, then my preferences are properly cyclic and I will be a money-pump. For let's say I have a ticket that entitles me to a red shirt next Monday; then suppose I trade that ticket for a yellow shirt ticket, then that one for a green shirt ticket, then I pay $1 to trade that for my original red shirt ticket. Assuming my preferences merely concern (i) what color shirt I wear on what day and (ii) my having more money than less, I will end up in a state that I think is worse than just having made no trade at all. This is so even though my preferences are not merely over shirt-colors and money, but rather coarse-grained sets of world-histories.
All that is needed for the pragmatic money-pump argument to go through is that my preferences are coarse-grained enough that we can speak of my making sequential choices as to which world-histories will obtain, such that facts about what choices I have made in these very cases do not influence the world-history in a way that makes a difference to my preferences. This seems pretty safe in the case of humans, and a result showing transitivity to be rationally required under such assumptions still seems important. Even in the case of a realistic agent who really likes paying to go through the A-B-C-A cycle, we could imagine alternate decision problems where they get to choose whether they get to go through that cycle during a future time-interval, and genuinely exploit them if those preferences are cyclic.
I worry that what I described above in the shirt-color example falls under what you mean by "or which only vary with time in some specified manner, rather than being totally unconstrained as your proposal would have it." A world-history is a specification of the world-state at each time, similar in kind to "I wear a red shirt next Monday." As I said before, the model would allow for weird fine-grained preferences over world-histories, but realistic uses of it will have as outcomes larger sets of world-histories like the set of histories where I wear a red shirt next Monday and have $1000, and so on. This is similar to how standard probability theory in principle allows one to talk about probabilities of propositions so specific that no one could ever think or care about them, but for practical purposes we just don't include those details when we actually apply it.
I'm concerned that I may be losing track of where our disagreement is. So, just to recap: I took your arguments in the OP to be addressed if we understand outcomes (the things to which utilities are assigned) to be world-histories or sets of world-histories, so we can understand the difference between an agent who's content with paying a dollar for every A-B-C-A cycle and an agent for whom that would be indicative of irrationality. You alleged that if we understand outcomes in this way, and not merely as possible states of the world with no reference to time, then (i) we cannot model sequential decisions, (ii) such a model would have an unrealistic portrayal of decision-making, and (iii) there will be too few constraints on preferences to get anything interesting. I reply: (i) sequential decisions can still be modeled as choices between world-histories, and indeed in an intuitive way if we make the realistic assumption that the agent's choices in this very sequence by themselves do not make a difference to whether a world-history is preferred; (ii) the decisions do seem to be intuitively modeled if we coarse-grain the sets of world-histories appropriately; and (iii) even if money-pump arguments only go through in the case of agents who have a certain additional structure to their preferences, this additional structure is satisfied by realistic agents and so the restricted results will be important. If I am wrong about what is at issue, feel free to just correct me and ignore anything I said under false assumptions.
If we wanted to be super proper, then preferences should have as objects maximally specific ways the world could be, including the whole history and future of the universe, down to the last detail. Decision theory involving anything more coarse-grained than that is just a useful approximation
Preferences can be equally rigorously defined over events if probabilities and utilities are also available. Call a possible world , the set of all possible worlds , and an a set such that an "event". Then the utility of is plausibly This is a probability-weighted average, which derives from dividing the expected utility by , to arrive at the formula for alone.
So if we have both a probability function and a utility function over possible worlds, we can also fix a Boolean algebra of events over which those functions are defined. Then a "preference" between two events is simply .
"Events" are a lot more practical than possible worlds, since events don't have to be maximally specific, and they correspond directly to propositions, which one can "believe" and "desire" to be true. Degrees of belief and degrees of desire can be described by probability and utility functions respectively.
Many propositions can be given event semantics, but with the caveat that events should still be parts of a space of possible worlds, so that "It's Friday" is not an event (while "When it's Friday, I try to check the mail" is).
Where do you think is the difference? I agree that there is a problem with indexical content, though this affects both examples. ("It's (currently) Friday (where I live).")
Even though it doesn't solve all problems with indexicals, it's probably better to not start with possible worlds but instead start with propositions directly, similar to propositional logic. Indeed this is what Richard Jeffrey does. Instead of starting with a set of possible worlds, he starts with a disjunction of two mutually exclusive propositions and :
An indexical proposition doesn't evaluate a possible world (in the sense of a maximally detailed world history), it evaluates a possible world together with a location or time or a subsystem (such as an agent/person) in it. But pointing to some location or subsystem that is already part of the world doesn't affect the possible world itself, so it makes little sense to have preference that becomes different depending on which location or subsystem we are looking at (from outside the world), while the world remains completely the same. The events that should be objects of preference are made of worlds, not of (world, embedded subsystem) pairs.
Whether "It's Friday" is not a property of a world, it's a property of a world together with some admissible spacetime location. You can't collect a set of possible world histories that centrally have the property of "It's Friday". On the other hand, "I try to make sure to check the mail on Fridays" is a property that does distinguish worlds where it's centrally true (for a specific value of "I"). In general, many observations are indexical, they tell you where you are, which version of you is currently affecting the world, and a policy converts those indexical observations into an actual effect in the world that can be understood as an event, in the sense of a set of possible worlds.
I mean I agree, indexicals don't really work with interpreting propositions simply as sets of possible worlds, but both sentences contain such indexicals, like "I", implicitly or explicitly. "I" makes only sense for a specific person at a specific time. "It's Friday (for me)", relative to a person and a time, fixes a set of possible worlds where the statement is true. It's the same for "I try to make sure to check the mail on Fridays".
After you bundle the values of free variables into the proposition (make a closure), and "I" and such get assigned their specific referents, "It's Friday" is still in trouble. Because if it gets the current time bundled in it, then it's either true or false depending on the time, not depending on the world (in the maximally detailed world history sense), and so it's either true about all worlds or none ("The worlds where it's Friday on Tuesday"), there is no nontrivial set-of-worlds meaning. But with the mail proposition (or other propositions about policies) there is no problem like that.
I think one issue with the "person+time" context is that we may assume that once I know the time, I must know whether it is Friday or not. A more accurate assessment would be to say that an indexical proposition corresponds to a set of possible worlds together with a person moment, i.e. a complete mental state. The person moment replaces the "person + time" context. This makes it clear that "It's Friday" is true in some possible worlds and false in others, depending on whether my person moment (my current mental state, including all the evidence I have from perception etc) is spatio-temporally located at a Friday in that possible world. This also makes intuitive sense, since I know my current mental state but that alone is not necessarily sufficient to determine the time of week, and I could be mistaken about whether it's Friday or not.
A different case is "I am here now" or the classic "I exist". Which would be true for any person moment and any possible world where that person moment exists. These are "synthetic a priori" propositions. Their truth can be ascertained from introspection alone ("a priori"), but they are "synthetic" rather than "analytic", since they aren't true in every possible world, i.e. in worlds were the person moment doesn't exist. At least "I exist" is false at worlds where the associated person moment doesn't exist, and arguably also "I am here now".
Yet another variation would be "I'm hungry", "I have a headache", "I have the visual impression of a rose", "I'm thinking about X". These only state something about aspects of an internal state, so their truth value only depends on the person moment, not on what the world is like apart from it. So a proposition of this sort is either true in all possible worlds where that person moment exists, or false in all possible worlds where that person moment exists (depending on whether the sensation of hungriness etc is part of the person moment or not). Though I'm not sure which truth value they should be assigned in possible worlds where the person moment doesn't exist. If "I'm thinking of a rose" is false when I don't exist, is "I'm not thinking of a rose" also false when I don't exist? Both presuppose that I exist. To avoid contradictions, this would apparently require a three-valued logic, with a third truth value for propositions like that in case the associated person moment doesn't exist.
This makes it clear that "It's Friday" is true in some possible worlds and false in others, depending on whether my person moment (my current mental state, including all the evidence I have from perception etc) is spatio-temporally located at a Friday in that possible world.
My point is that the choice of your person moment is not part of the data of a possible world, it's something additional to the possible world. A world contains all sorts of person moments, for many people and at many times, all together. Specifying a world doesn't specify which of the person moments we are looking at (or from). Whether "It's Friday" or not is a property of a (world, person-moment) pair, but not of a world considered on its own.
Keeping this distinction in mind is crucial for decision theory, since decisions are shaping the content of the world, in particular multiple agents can together shape the same world. The states of the same agent at different times or from different instances ("person moments") can coordinate such shaping of their shared world. So the data for preference should be about what matters for determining a world, but not necessarily other things such as world-together-with-one-of-its-person-moments.
If we wanted to be super proper, then preferences should have as objects maximally specific ways the world could be, including the whole history and future of the universe, down to the last detail. Decision theory involving anything more coarse-grained than that is just a useful approximation
If X is better than Y, that gives no guidance about 40% chance of X being better or worse than 60% of Y. Preference over probability distributions holds strictly more data than preference over pure outcomes. Almost anything (such as actions-in-context) can in principle be given the semantics of a probability distribution or of an event in some space of maximally specific or partial outcomes, so preference over probability distributions more plausibly holds sufficient data.
Yeah, you're correct--I shouldn't have conflated "outcomes" (things utilities are non-derivatively assigned to) with "objects of preference." Thanks for this.
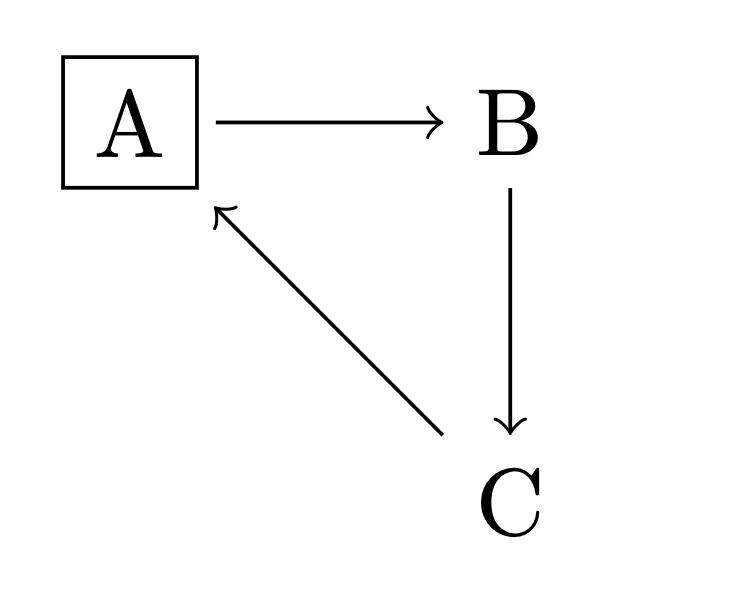
I think your setup is weird for the context where people talk about utility functions, circular preferences, and money-pumping. “Having a utility function” is trivial unless the input to the utility function is something like “the state of the world at a certain time in the future”. So in that context, I think we should be imagining something like this:

And the stereotypical circular preference would be between “I want the world to be in State {A,B,C} at a particular future time T”.
I think you’re mixing up an MDP RL scenario with a consequentialist planning scenario? MDP RL agents can make decisions based on steering towards particular future states, but they don’t have to, and they often don’t, especially if the discount rate is high.
“AI agents that care about the state of the world in the future, and take actions accordingly, with great skill” are a very important category of AI to talk about because (1) such agents are super dangerous because of instrumental convergence, (2) people will probably make such agents anyway, because people care about the state of the world in the future, and also because such AIs are very powerful and impressive etc.
I agree that the money pump argument is confusing. I think the real problem with intransitive preferences is that they're self-contradictory. If I have an intransitive preference and you simply ask me whether I want A, B, or C, I am unable to answer. As soon as I open my mouth to say something I already want to change my mind, and I'm stuck. However, there's some conceptual slippage to merely wanting to move in a cycle between states over time, such as wanting to travel endlessly from Chicago to New York to San Francisco and back to Chicago again. This may be considered silly and wasteful but there's nothing inherently illogical about it.
There are no actions in decision theory, only preferences. Or put another way, an agent takes only one action, ever, which is to choose a maximal element of their preference ordering. There are no sequences of actions over time; there is no time. To bring sequences of actions into the fold of "decision theory", the outcomes of those sequences would be the things over which the preference ordering ranges, and once again there is only the action of choosing a most preferred. In the limit, there is only the single action of choosing the most preferred entire future history of the agent's actions, evaluated according to their influence on the agent's entire future light-cone, and their preference over different possible future light-cones. But this is absurdly impractical, and this is "monkeys typing Shakespeare" levels of impracticality, not mere Heath Robinson.
This, I think, is a weakness of "decision theory", which might better be called "preference theory". For example, the SEP article on decision theory hardly mentions any of the considerations you bring up.
There are no actions in decision theory, only preferences. Or put another way, an agent takes only one action, ever, which is to choose a maximal element of their preference ordering. There are no sequences of actions over time; there is no time.
That's not true. Dynamic/sequential choice is quite a large part of decision theory.
It seems that the OP is simply confused about the fact that preferences should be over the final outcomes - this response equivocates a bit too much.
Though the usual money pump justification for transitivity does rely on time and a "sequence of actions". Which is strange insofar decision theory doesn't even model such temporal sequences.
Yes, the money pump argument is an intuition pump for transitivity. Yet it is not formalised within, say, the VNM or Savage axioms, but is commentary upon them. The common response to it, that “I’d notice and stop doing that” goes outside the scope of the theory.
Game theory takes things further, as do things like Kelly betting and theories that prescribe not individual actions but policies, but my impression is that there is as yet no unified theory of action over time in a world that is changed by one’s actions.
I might be missing something that's written on this page, including comments, but if not, here is a vague understanding of mine of what people might fear regarding money pumps. I'm going to diverge from your model a bit, and use the concept of sub-world-state, denoted A', B', and C', which includes everything related to the world that can be preferred except for how much money you have, which I handle separately in this comment.
A' -> B' -> C' -> A' preferences hold in a cycle.
-> preference also holds for money had.
I think, agents, either intrinsically, or instrumentally, (have to) simplify their decisions by factoring them at each timestep.
So they ask themselves:
Do I prefer going from A' -> B' more than having -> , more concretely -> ?
In this example, the non-money preference is strong, so the answer is clearly yes.
Even if the agent plans ahead a bit, and considers:
Do I prefer A' -> B' -> C' more than having -> ?
The answer will still be a clear yes.
The interesting question is, what might someone who fears money pumps say an agent would do if it occurs to them to plan ahead enough and consider:
Do I prefer A' -> B' -> C' -> A' more than having -> ?
According to both this and your formalisms, this agent should clearly realize that they much prefer -> and stay put at A'. And I think you are correct to ask whether planning is allowed by these different formalisms, and how it fits in.
I think concerns come in two flavors:
One is how you put it: if the agent is stupid, (or more charitably, computationally bounded, as we all are) they might not realize that they are going in circles and trading away value in the process for no (comparable(?)) benefit to themselves. Maybe agents are more prone to notice repetition and stop after a few cycles, since prediction and planning are famously hard.
The other concern is what we seem to notice in other humans and might notice in ourselves as well (and therefore might in practice diverge from idealized formalisms): sometimes we know or strongly suspect that something is likely not a good choice, and yet we do it anyway. How come? One simple answer can be how preference evaluations work in humans, if A' -> B' is strongly enough preferred in itself, knowing or suspecting A' -> B' -> C' -> A' + -> might not be strong enough to override it.
It might be important that, if we can, we construct agents that do not exhibit this 'flaw'. Although one might need to be careful with such wishes since such an agent might monomaniacally pursue a peak to which it then statically sticks if reached. Which humans might dis-prefer. Which might be incoherent. (This has interested me for a while and I am not yet convinced that human values do not contain some (fundamental(?)) incoherence, e.g. in the form of such loops. For better or for worse I expanded a bit on this below, though not at all very formally and I fear less than clearly.)
So in summary, I think that if an agent
- has static preferences over complete world states
- is computationally boundless (enough), plans, and
- does not 'suffer' from the kind of near-term bias that humans seem to
then it cannot be made worse by money pumps around things it cares about.
I think your questions are very important to be clear on as much as we can, and I only responded to a little bit of what you wrote. I might respond to more, hopefully in a more targeted and clear way, if I have more time later. And I also really hope that others also provide answers to your questions.
Some bonus pondering is below, much less connected to your post just felt nice to think through this a little and perhaps invite others' thoughts on as well.
Let's imagine the terminus of human preference satisfaction. Let's assume that all preferences are fulfilled, importantly enough: in a non-wire-headed fashion. What would that look like, at least abstractly?
a) Rejecting the premise: All (human) preferences can never be fulfilled. If one has n dyson spheres, one can always wish for n+1. There will always be an orderable list of world states that we can inch ever higher on. And even if it's hard to imagine what might someone desire if they could have everything we currently can imagine--by definition--new desires will always spring up. In a sense, dissatisfaction might be a constant companion.
b) We find a static peak of human preferences. Hard to imagine what this might be, especially if we ruled out wireheading. Hard to imagine not dis-preferring it at least a little.
c) A (small or large) cycle is found and occupied at the top. This might also fulfill the (meta-)preference against boringness. But it's hard to escape that this might have to be a cycle. And if nothing else we are spending negentropy anyway, so maybe this is a helical money-pump spiral to the bottom still?
d) Something more chaotic is happening at the top of the preferences, with no true cycles, but maybe dynamically changing fads and fashions, never much deviating from the peak. This is hard to see how or why states would be transitioned to and from if one believes in cardinal utility. This still spends negentropy, but if we never truly return to a prior world-state even apart from that, maybe it's not a cycle in the formal sense?
I welcome thoughts and votes on the above possibilities.
I suspect there's a LOT of handwaving in trying to apply theory to actual decisions or humans. These graphs omit time, so don't include "how long spent in worse states, and how long the preferred state lasts" in their overall preference ordering. In known agents (humans), actual decisions seem to always include timeframes and path-dependency.
You can in fact have an agent who prefers to be money pumped. And from their perspective there is no problem with that.
Money pumps isn't a universal argument that could persuade a rock to turn into a brain. It's just an appeal to our own human intuitions.
It seems correct that if you have a planner operating over the full set of transition you'll ever see, the it can avoid money-pumping of this kind. However it doesn't seem to hold that this prevents money-pumping in general.
Consider, you have a preference that at some specific future time you will get C > B > A > C, and this preference is independent of how much cash you have. You have a a voucher that will pay out to A at that time, which you value only instrumentally. You start with no access to any trades.
Someone comes up to you and offers you a voucher for B in exchange for your voucher for A and epsilon cash. Let's not assume any knowledge of any future trades you might be offered. What decision do you make? If a preference is useful for anything it surely should inform you what decision to make, and if preference is meant for anything it should surely say that the chosen actions result in it. If the result of planning is anything but ‘take the trade’ I don't know what properties this preference ordering has that would give it that label.
Though, I suppose this argument generalizes. If you believe only C > B > A, you might still take a trade from B to A if you expect it's sufficiently more probable to let you trade to C. If you have persistently wrong non-static expectations, those might be pumped for money the same way. Another way to put this is maybe that trying to value access to states independently of their trade value doesn't work.
I've no doubt that it's possible to make a planner that's somewhat robust to inconsistent preference ordering, but this does seem driven by the fact we've not given the term ‘preference ordering’ any coherent meaning yet and have no coherent measure of success. Once you demand those it would be easier to point at any flaws.
I, too, have had the same objection you have with people that claim that the problem with intransitive preferences is that you can be money pumped, and that our real objection is just that it'd be really weird to be able to transition by stepwise preferred states and yet end up in a state dispreferred to the start (this not being a money pump because the agent can just choose not to do this).
Though, "it's really weird" is a pretty good objection - it, in fact, would be extremely weird to have intransitive preferences, and so I think it is fine to assume that the "true" (Coherent Extrapolated Volition) preferences of e.g. humans are transitive.
You can use the intuition that a greedy optimizer shouldn't ever end up worse than it started, even if it isn't in the best place.
I think it is fine to assume that the "true" (Coherent Extrapolated Volition) preferences of e.g. humans are transitive.
I think this could be safe or unsafe, depending on implementation details.
By your scare quotes, you probably recognize that there isn't actually a unique way to get some "true" values out of humans. Instead, there are lots of different agent-ish ways to model humans, and these different ways of modeling humans will have different stuff in the "human values" bucket.
Rather than picking just one way to model humans, and following it and only it as the True Way, it seems a lot safer to build future AI that understands how this agent-ish modeling thing works, and tries to integrate lots of different possible notions of "human values" in a way that makes sense according to humans.
Of course, any agent that does good will make decisions, and so from the outside you can always impute transitive preferences over trajectories to this future AI. That's fine. And we can go further, and say that a good future AI won't do obviously-inconsistent-seeming stuff like do a lot of work to set something up and then do a lot of work to dismantle it (without achieving some end in the meantime - the more trivial the ends we allow, the weaker this condition becomes). That's probably true.
But internally, I think it's too hasty to say that a good future AI will end up representing humans as having a specific set transitive preferences. It might keep several incompatible models of human preferences in mind, and then aggregate them in a way that isn't equivalent to any single set of transitive preferences on the part of humans (which means that in the future it might allow or even encourage humans to do some amount of obviously-inconsistent-seeming stuff).
If you really have preferences over all possible histories of the universe, then technically you can do anything.
Money pumping thus only makes sense in a context where your preferences are over a limited subset of reality.
Suppose you go to a pizza place. The only 2 things you care about are which kind of pizza you end up eating, and how much money you leave with. And you have cyclic preferences about pizza flavor A<B<C<A.
Your waiter offers you a 3 way choice between pizza flavors A, B, C. Then they offer to let you change your choice for $1, repeating this offer N times. Then they make your pizza.
Without loss of generality, you originally choose A.
For N=1, you change your choice to B, having been money pumped for $1. For N=2, you know that if you change to B the first time, you will then change to C, so you refuse the first offer, and then change to B. The same goes for constant known N>2, repeatedly refuse, then switch at the last minute.
Suppose the waiter will keep asking and keep collecting $1 until you refuse to switch. Then, you will wish you could commit yourself to paying $1 exactly once, and then stopping. But if you are the sort of agent that switches, you will keep switching forever, paying infinity $ and never getting any pizza.
Suppose the waiter rolls a dice. If they get a 6, they let you change your pizza choice for $1, and roll the dice again. As soon as they get some other number, they stop rolling dice and make your pizza. Under slight strengthening of the idea of cyclical preferences to cover decisions under uncertainty, you will keep going around in a cycle until the dice stops rolling 6's.
So some small chance of being money pumped.
Money pumping is an agent with irrational cyclic preferences is quite tricky, if the agent isn't looking myopically 1 step ahead but can forsee how the money pumping ends long term.
I noticed recently is that there are two types of preference and that confusing them leads to some of the paradoxes described here.
- Desires as preferences. A desire (wanting something) can loosely be understood as wanting something which you currently don't have. More precisely, a desire for X to be true is preferring a higher (and indeed maximal) subjective probability for X to your current actual probability for X. "Not having X currently" above just means being currently less than certain that X is true. Wanting something is wanting it to be true, and wanting something to be true is wanting to be more certain (including perfectly certain) that it is true. Moreover, desires come in strengths. The strength of our desire for X corresponds to how strongly you prefer perfect certainty that X is true to your current degree of belief that X is true. These strengths can be described by numbers in a utility function. In specific decision theories, preferences/desires of that sort are simply called "utilities", not "preferences".
- Preferences that compare desires. Since desires can have varying strengths, the desire for X can be stronger ("have higher utility") than the desire for Y. In that sense you may prefer X to Y, even if you currently "have" neither X nor Y, i.e. even if you are less than certain that X or Y is true. Moreover, you may both desire X and desire Y, but preferring X to Y is not a desire.
Preferences of type 1 are what arrows express in your graphs (even though you interpret the nodes more narrowly as states, not broadly as propositions which could be true). means that if is the current state, you want to be in . More technically, you could say that in state you disbelieve that you are in state , and the arrow means you want to come to believe you are in state . Moreover, the desires inside a money pump argument are also preferences of type 1, they are about things which you currently don't have but prefer to have.
What about preferences of type 2? Those are the things which standard decision theories call "preferences" and describe with a symbol like "". E.g. Savage's or Jeffrey's theory.
Now one main problem is that people typically use the money pump argument that talks about preferences of type 1 (desires/utilities) in order to draw conclusions about preferences of type 2 (comparison between two desires/utilities) without noticing that they are different types. So in this form, the argument is clearly confused.
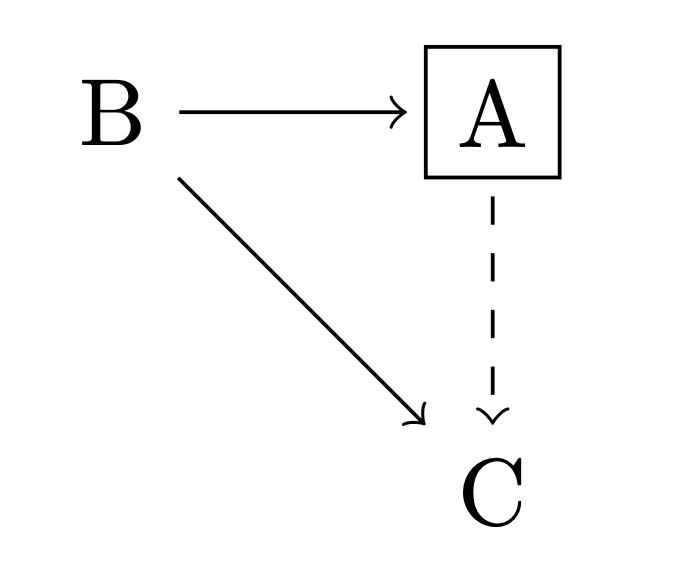
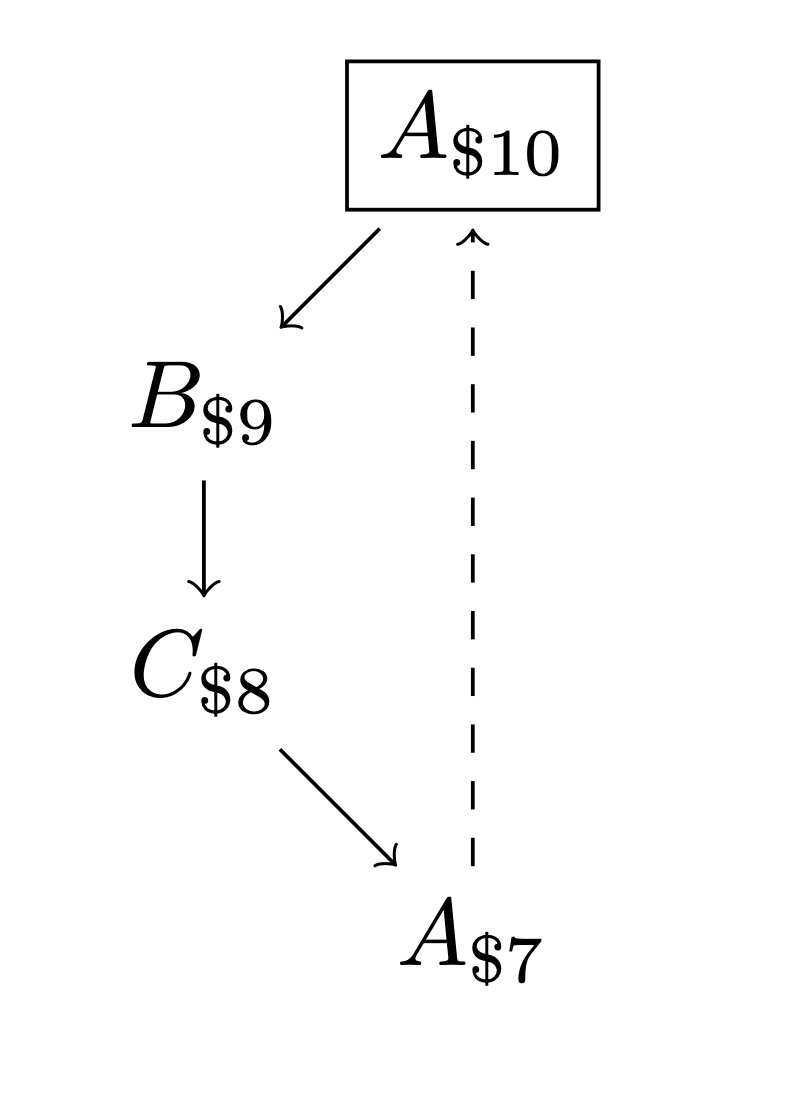
The inference goes beyond the definition and claims, additionally, that in a case like this diagram, the agent will only take actions that "follow the arrows," changing the world state from less-preferred to more-preferred at each step.
Hmm. I'm not sure about that inference but might be due to absence of specific argument you're making that inference from.
The preference arrow to me is simply pointing in a direction. The path between the less preferred state to more preferred state is pretty much a black box at this point. So I think the inference is more like: If agent 86 stays in state A, there is a lack of resources or a higher transition cost to get from A to C than a difference in utility/value between the two states.
There is probably something of a granularity here as well. Does taking a second job for a while, or doing some type of gig-work one doesn't enjoy at all, count as a state or is that wrapped up in some type of non-preference type of state?
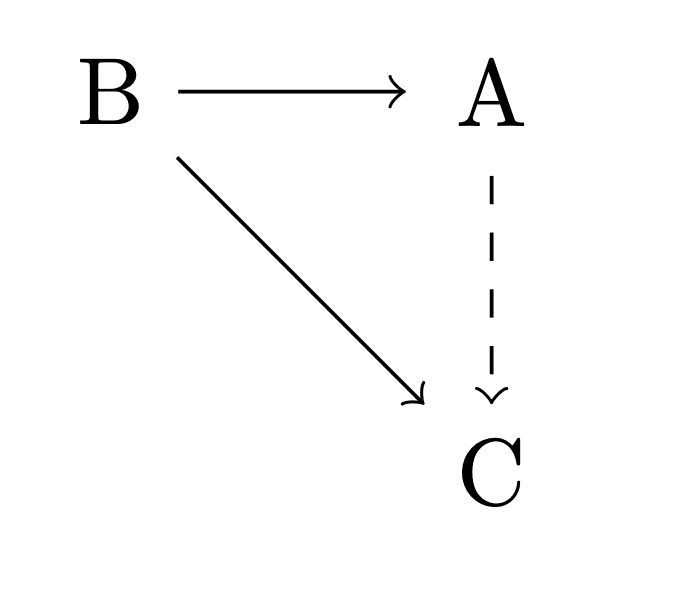
I'm not sure if I agree that this idea with the dashed lines, of being unable to transition "directly," is coherent or not. A more plausible structure seems to me like a transitive relation for the solid arrows. If A->B and B->C, then there exists an A->C.
Again, what does it mean to be unable to transition "directly?" You've explicitly said we're ignoring path depencies and time, so if an agent can go from A to B, and then from B to C, I claim that this means there should be a solid arrow from A to C.
Of course, in real life, sometimes you have to sacrifice in the short term to reach a more preferred long term state. But by the framework we set up, this needs to be "brought into the diagram" (to use your phrasing.)
You've explicitly said we're ignoring path depencies and time
I wasn't very clear, but I meant this in a less restrictive sense than what you're imagining.
I meant only that if you know the diagram, and you know the current state, you're fully set up to reason what the agent ought to do (according to its preferences) in its next action.
I'm trying to rule out cases where the optimal action from a state depends on some extra info beyond the simple fact that we're in , such as the trajectory we took to get there, or some number like "money" that hasn't been included in the states yet is still supposed to follow the agent around somehow.
But I still allow that the agent may be doing time discounting, which would make A->B->C less desirable than A->C.
The setup is meant to be fairly similar to an MDP, although it's deterministic (mainly for presentational simplicity), and we are given pairwise preferences rather than a reward function.
Preference doesn't compare what you have to what you might be able to get, it compares with each other the alternatives you might be able to enact. Expected utility theory is about mixed outcomes, but in case of an algorithm making the decision the alternatives become more clearly mutually exclusive, it becomes logically impossible for different alternatives to coexist in any possible world.
A closed term, that is an algorithm without arguments, can't change what it outputs from the thing it does output to some different thing. So you really can't move from one of the possibilities to the other, if it's not part of some process of planning that is happening prior to actually enacting any of the possible decisions.
Preference doesn't compare what you have to what you might be able to get, it compares with each other the alternatives you might be able to enact.
This is a plausible assumption (@Steven Byrnes made a similar comment), yet the money pump argument apparently does compare what you have to what you might get in the future.
You touch on the point that people can mean several different things when talking about preferences. I think this causes most of the confusion and subsequent debates.
I wrote about this from a completely different perspective recently.
Responding mostly to your first bit rather than the circular preferences.
But note, now, that the course of action I just said was "obviously" correct involves going "the wrong way" across the arrow connecting A to B.
This isn't a failure of greedy maximization, but rather a failure of following your proposal in the first "diagrams" section about including everything you care about into the graph.
That is, having a reachable path from A -> B and B -> C but not A -> C implicitly means that you care about the ordering, like as a sense of time or the effects of being in state B. You've failed to encode your preferences into the graph, because that is a valid set of preferences by itself.
A common way of "fixing" this is to just say the graph must be transitive. If there's a path from A -> B and B -> C there must be on from A -> C, likely defined by composition like your proposed plan.
Of course, here I'm taking the position of an arrow meaning the agents prefer going down an arrow and prefers that as a route. If you don't have a route from A -> C, then there must be some fact of the world that makes moving through B a problem. I think your first sections confusion is just not actually putting all the relevant information into the graph.
This seems like it's equivocating between planning in the sense of "the agent, who assigns some (possibly negative) value to following any given arrow, plans out which sequence of arrows it should follow to accumulate the most value*" and planning in the sense of "the agent's accumulated-value is a state function". The former lets you take the detour in the first planning example (in some cases) while spiralling endlessly down the money-pump helix in the cyclical preferences example; the point of money pump arguments is to get the latter sort of planning from the former by ruling out (among other things) cyclical preferences. And it does so by pointing out exactly the contradiction you're asking about; "the fact that we can't meaningfully define planning over [cyclic preferences]" (with "planning" here referring to having your preferences be a state function) is precisely this.
The anthropomorphisation of the agent as thinking in terms of states instead of just arrows (or rather, due to its ability to plan, the subset of arrows that are available) is the error here, I think. Note that this means the agent might not end up at C in the first example if, eg, the arrow from A to B is worse than the arrow from B to C is good. But C isn't its "favourite state" like you claim; it doesn't care about states! It just follows arrows. It seems like you're sneaking in a notion of planning that is basically just assuming something like a utility function and then acting surprised when it yields a contradiction when applied to cycles.
*I guess I'm already assuming that the arrows have value and not just direction, but I think the usual money pump arguments kinda do this already (by stating the possibility of exchanging money for arrow); I'm not sure how you'd get any sort of planning without at least this
In higher dimensional spaces, assuming something like a continuous preference function, it should become increasingly likely for desired outcomes to be achievable by a series of myopic decisions. This is similar to how gradient descent works (and evolution, to a much lesser extent, due to its statistical tolerance for mild negative traits).
Given that the real world is immensely high dimensional, I would expect the most efficient optimisation function for a ML agent to learn would be somewhat myopic, and avoid this issue.
It’s very simple. We have the following assumptions (axioms):
- for any two states, you prefer one over the other, or, you are indifferent, we will say A > B to mark A is preferred over B, A~B to say that you are indifferent, and A ≥ B to say you are either preferring A or you are indifferent.
- if A ≥ B and B ≥ C, then A ≥ C, and at the same time A ~ C iff both A ~ B and B ~ C.
- ~ is equivalency relation (behaves like =)
The conclusion of above assumptions is no cycles. Now, each of them seems as a reasonable assumption. Sure, we can choose different set of axioms, but why? What are we trying to model?
This felt to me like it was something that could be reframed through category theory but I'm not the best at explaining it so here's my Terence Tao Claude giving it's best shot?:
Nostalgebraist has identified a fundamental confusion that elegantly reveals itself through category theory. What's happening is that discussions about preference orderings conflate two distinct mathematical structures without acknowledging the switch. (It's using Steven Byrnes comment and going through a similar comparison from the perspective of category theory to more cleanly restate the confusion.)
Claude Tao:
Two Distinct Categories
Category theory offers a clear framework for understanding this confusion. A category consists of objects, morphisms (arrows) between them, and rules for composition. The crucial insight is that preference orderings can be modeled as two different categories:
The Decision Theory Category (DT)
- Objects: World states (A, B, C)
- Morphisms: Pure preference relations where A→B means "B is preferred over A"
- Composition Rule: If A→B and B→C, then A→C (transitivity)
- Key Property: Arrows represent what would be chosen if all transitions were available
The Reinforcement Learning Category (RL)
- Objects: Same world states (A, B, C)
- Morphisms: Optimal policies where A→B means "move from A to B is the optimal action"
- Composition Rule: Multi-step planning that maximizes value
- Key Property: Arrows incorporate both preference and availability information
Exactly Matching Nostalgebraist's "Two Readings"
These categories precisely correspond to nostalgebraist's two interpretations:
- "Give up on the inference" = Use the DT category, where arrows represent pure preferences that don't dictate actions
- "Refuse to pick arrow orientations until..." = Use the RL category, where arrows represent planned behavior
The Money Pump Confusion
The money pump argument inadvertently mixes these categories in exactly the way nostalgebraist describes. It:
- Starts by defining preference cycles in the DT category (pure preference relations)
- Then claims these are problematic by applying reasoning from the RL category (assuming agents follow arrows)
But as nostalgebraist correctly points out, an agent capable of planning won't blindly follow preference arrows when doing so leads to a worse outcome. In the RL category, such cycles simply wouldn't exist in the optimal policy graph if the state space properly includes resources like money.
The Example Problem
Consider nostalgebraist's example where A→C and C→B→A forms a cycle:
- In the DT category: This represents cyclical pure preferences, which may be mathematically problematic but don't automatically lead to money pumps
- In the RL category: If planning is allowed, the agent would see the resource loss and avoid completing the cycle
The confusion arises when we use DT-category arrows but assume RL-category behaviors. As nostalgebraist notes, this implicitly requires "the agent is kind of stupid (i.e. it can't plan)" as a side assumption.
Mathematical Clarity
This categorical distinction explains why formal RL treatments avoid this confusion. They cleanly separate:
- Reward functions (belonging to the DT category)
- Transition functions (describing available state transitions)
- Value functions and policies (belonging to the RL category)
The problem occurs when we try to reason about "rational preferences" without explicitly stating which category we're working in.
Conclusion
Nostalgebraist's insight is precisely correct: the confusion about preference orderings stems from mixing two different mathematical structures. By maintaining categorical discipline – being clear about whether our arrows represent pure preferences or optimal actions – we can avoid the apparent paradoxes in money pump arguments and similar discussions.
The question isn't which category is "right," but recognizing that they model different aspects of decision-making and being explicit about which one we're using at any given time.
Curated and popular this week