I don't have an answer to your question, but I do have a concern: beware of positive bias. Don't just look for positive examples--how many trends are not precisely exponential? I'm pretty sure the answer is "a lot." (I know it sounds basic, but it bears repeating.)
More crucially, how many trends almost, but not quite look precisely exponential? Are precisely-exponential trends the tip of a long tail, or an additional local mode?
The logistic curve, for example, is extremely similar to the exponential curve for small values seeing as the latter is y' = ky and the former is y' = ky(1-y). That got Malthus with his whole doomsday arguments about population growth outstripping resources (at least for the time being).
Any time the current growth rate depends linearly on the size of the current population, you get exponential growth.
For instance, given effectively boundless food, the number of bacteria will double every regular time period because, in that time period, each bacterium can split into more.
Similarly, human populations grow exponentially (up to environmental bounds like food supply, war, etc.) because after roughly twenty years, humans beget more humans. With a population as gargantuan as Earth's, that growth rate is practically continuous.
Kurzweil's argument is that this applies to many technological industries, too. Faster, more powerful computers make it easier and faster to design the next technological generation. Thus when you measure computing power with any one well-defined scale like transistor count, you'll find that the growth rate depends on the current number. Ergo, exponential.
I'm not sure what's going on with the GDP, but if it's really keeping so nicely to an exponential curve like that, then I'd expect it means that the growth in GDP depends primarily on the current GDP and that it has been this way for a very long time.
I don't know whether this is what's really going on. As others here have pointed out, there might be some biases playing a role here. And as I suspect has been beaten to death here before, Kurzweil hides a number of dubious assumptions about market forces and human creativity in his projections. But I do know that if you really, honestly have a strongly exponential growth pattern, it's most likely that you'll find some reason why the growth rate depends on the current population.
the growth in GDP depends primarily on the current GDP and that it has been this way for a very long time.
If this were the case, we should expect any noise to accumulate as a random walk. After the Great Depression, the data goes back to where it would have been without the interruption.
GDP trend related to population, not to previous GDP? Over the period of time covered by the above GDP graph, the log graph of US population (seen on http://www.wolframalpha.com/input/?i=united+states+population) looks pretty much like a straight line. GDP per person looks exponential over the last ~60 years (also wolframalpha) [edit] looks linear in constant dollars (from wikipedia)[/edit]
Unless an economic disruption is big enough to greatly change the birth or death rates, the GDP will tend to go back to the straight line, it seems.
If there is easy-to-find GDP data going back to the 1600s, when the log(population) graph is not on the same line as recently, my guess could be tested.
Alternatively, we could examine both datasets closely to see if non-trend-predicted variation in one is reflected in the other.
I should perhaps have said in the OP that I understand the natural examples perfectly well; what startles me is that here I'd expect certain exogenous factors (the introduction of income tax and its later peak and descent, the rise and fall of the automobile industry, World War I and the Cold War, etc) to have some significant effects on the growth rate, and different effects in different eras.
Instead, it looks to me (with the exception of the Great Depression and recovery) like the growth rate never leaves the 3-4% range, once you average over decades to iron out the fluctuations. I noticed that this confused me.
Could there be an economic-technocratic explanation of the steadiness of growth since 1950? That is, did someone decide that annual GNP growth should be 3.5% (which is 2% growth per capita, according to Kehoe's graph), and has policy been determined accordingly?
The Federal Reserve does play a relevant role, and it may well have tried to keep growth within a narrow band over the last two decades. If so, then the financial crisis might have started to show that the official GDP numbers of the last decade were a house of cards based on overvaluation of some sectors of the economy, and that we've actually been growing at a lower rate for quite some time.
I don't have evidence of this, but it is a hypothesis that confuses me less than the hypotheses of coincidence or a natural propensity to a 3.5% growth rate.
Abusing linear regression makes the baby Gauss cry... It's true that fitting lines on log-log graphs is what Pareto did back in the day when he started this whole power-law business, but "the day" was the 1890s. There's a time and a place for being old school; this isn't it. - Cosma Shalizi
Great link, thanks! I can't tell, though, whether this caution extends to graphs of change over time, in addition to sets of (supposedly independent) data points with a conjectured power law.
For comparison, here's a relevant example of a log-log graph (also from FiveThirtyEight) of an exponentially growing quantity which doesn't appear to show such a steady rate of growth:
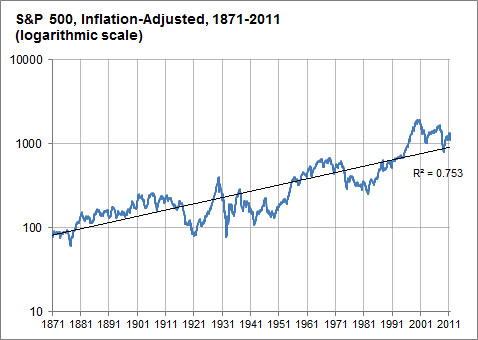
The difference between this graph and the GDP graph is pretty striking.
Fascinating question. I share your curiosity, and I'm not at all convinced by any attempted explanations so far. Further, I note that the trend makes a prediction: an economic crunch will be followed by a swell of corresponding magnitude. So who wants to go invest in the US stock market now?
Would they look so precisely exponential, with exactly the same exponent, if we fit 5-10 log-linear lines to the graph rather than one? Eyeballing it, looks like the answer is no...
Moore's Law is one big idea (Feynman's "There is plenty of room at the bottom") filtered through the conservative engineering practice of not doing too much in one go. Much of engineering proceeds in 20% or 50% increments. Steam trains get more powerful, bridges longer, mines deeper, ships larger, all in percentage increments over the previous record holder.
Technological advances affect GDP as they become mainstream. This requires knowledge propagation in which teachers teach a students, some students become teachers and teach more students,... They say that Faraday discovered electromagnetic induction on 29th August 1831, but by the time this hit the GDP figures with the electrification of American industry in the 1920's and 1930's it had been smeared out an exponential take up on a decades time-scale determined by human factors.
Hmm, my observations don't actually lead to a prediction of a steady rate of growth.
One the other hand, the attention to human factors hints that there might be a fairly low maximum rate of growth of around 3.5% a year, set by the proportion of good students in a population. One notices how steam railway trains stagnated from err, 1910 (not too sure) but they got to 4% thermal efficiency and then all the bright young engineers went into automobiles and aviation, and steam trains remained crap until diesel -electrics came along.

http://www.greatplay.net/offsite/us-econ-growth.png
When you look at a graph of the growth rate itself, the data doesn't look like a perfect fit for a line anymore.
Instead, I think the 3.5% is an average that looks good when you have a graph that is rather zoomed out, but overall isn't that much of some sort of pattern that needs explaining.
Instead, the economy seems to fluctuate and cycle a lot, and we already have some theories of business cycles to explain why that is so.
You can also see points in history where certain geopolitical events caused lower or higher than average growth, so the idea that the GDP is seemingly immune to geopolitical events is hardly there in actuality.
~
I can't explain Moore's Law (that's an area I haven't studied at all), but I'd be willing to wager that if you looked at the graph of growth like this, you would see some fluctuations as well. (No negative growth though, obviously.)
It would be interesting to see. If the Moore's Law graph really didn't fluctuate much, then I think you have something in need of explaining.
~
Also, you might be wondering something like "if technology has improved drastically, why hasn't GDP growth shot up to something wild like 7% per year?". But growth itself requires more and more change every year just to keep at a constant growth percentage, and as Moore's Law shows, technology itself improves at a mostly exponential rate, so we would only expect the same exponential increase in GDP, not something more-exponential-than-exponential.
Hey, what happened to your graph?
Anyway, it seemed to me that if you calculated GDP change over 10-year periods in order to drown out year-to-year fluctuations and business cycles, that you'd have essentially constant 3.5% annualized change except for the 1930s and 1940s. The absence of long-term trends is what confuses me.
If there's no convincing natural explanation, there's likely a human one. The human sense of scale or progress is vaguely exponential, so it's possible that some trends are exponential because humans work to make it that way so that things seem like steady progress.
Why would they care about it that much? If they're spending more money than it's worth to keep up the pace, or if they're intentionally slowing down their R&D, they're leaving a vast gap for a competitor to kick them out of the market.
You have successfully predicted the past ;-) With the Pentium 4, Intel deliberately went for the highest possible clock rate, because that looked good in marketing - at the expense of actual performance. This gave their main competitor, AMD, a massive opening for their then-current lines of processor, which did better in performance per clock, per watt and per dollar. Intel only recovered by going back to the P-III and developing the P-M and Core line from there.
I moved this comment to fall under Tetronian's, and was surprised to learn that deletion no longer seems to work.
If you can read this comment, then I'm also kind of irritated about it. If you really want to delete a comment's contents, you can edit it to be blank, but that looks ugly. There ought to be a proper deletion option somewhere, at least for the first hour or so after posting.
I was reading a post on the economy from the political statistics blog FiveThirtyEight, and the following graph shocked me:
This, according to Nate Silver, is a log-scaled graph of the GDP of the United States since the Civil War, adjusted for inflation. What amazes me is how nearly perfect the linear approximation is (representing exponential growth of approximately 3.5% per year), despite all the technological and geopolitical changes of the past 134 years. (The Great Depression knocks it off pace, but WWII and the postwar recovery set it neatly back on track.) I would have expected a much more meandering rate of growth.
It reminds me of Moore's Law, which would be amazing enough as a predicted exponential lower bound of technological advance, but is staggering as an actual approximation:
I don't want to sound like Kurzweil here, but something demands explanation: is there a good reason why processes like these, with so many changing exogenous variables, seem to keep right on a particular pace of exponential growth, as opposed to wandering between phases with different exponents?
EDIT: As I commented below, not all graphs of exponentially growing quantities exhibit this phenomenon- there still seems to be something rather special about these two graphs.