The command to spread observations rather than theories is a valuable one. I often find it to result in far less confusion.
That said, I'm not sure it follows from a paper. You say it implies
Passing along theories can actually make both understanding and performance worse.
This wasn't found. Here are the two relevant screenshots (the opening line is key, and then the graph also shows no real difference).

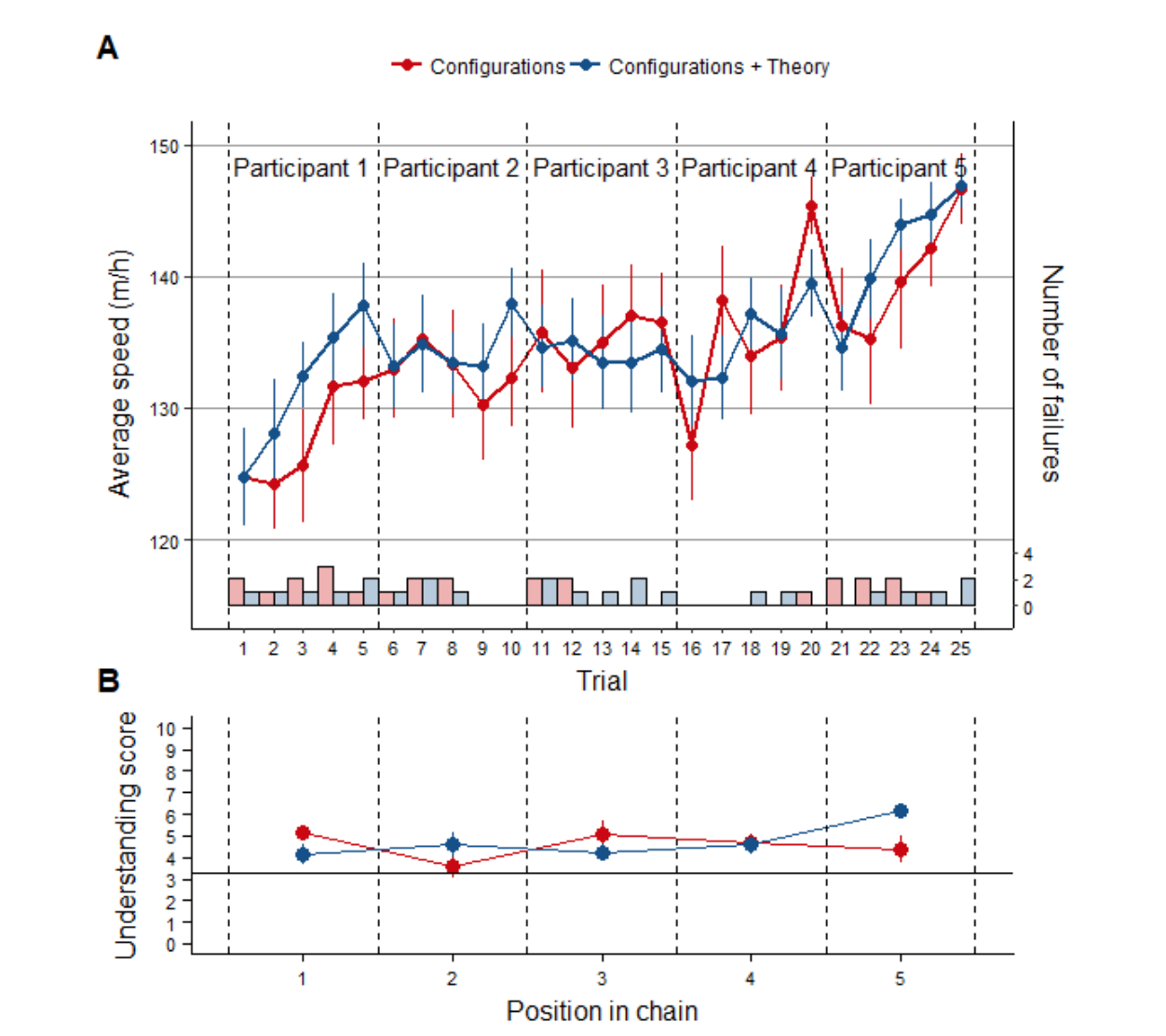
Passing along theories didn't make things worse, the two groups (data vs data+theory) were equally good.
Thanks for pointing this out. I think the OP might have gotten their conclusion from this paragraph:

(Note that, in the web page that the OP links to, this very paragraph is quoted, but for some reason "energy" is substituted for "center-of-mass". Not sure what's going on there.)
In any case, this paragraph makes it sound like participants who inherited a wrong theory did do worse on tests of understanding (even though participants who inherited some theory did the same on average of those who inherited only data, which I guess implies that those who inherited a right theory did better). I'm slightly off-put by the fact that this nuance isn't present in the OP's post, and that they haven't responded to your comment, but not nearly as much as I had been when I'd read only your comment, before I went to read (the first 200 lines of) the paper for myself.
I'm not convinced you're drawing the right conclusion. Here's my take:
The person who has taken a class in mechanics has been given a theory, invented by someone else, which happens to be quite good. Being able to apply an existing theory and being able to create a new theory are different skills. One of the key skills of being able to create your own theories is getting good at noticing anomalies that existing theories don't account for:
The mystery is how a conception of the utility of outcomes that is vulnerable to such obvious counterexamples survived for so long. I can explain it only by a weakness of the scholarly mind that I have often observed in myself. I call it theory-induced blindness: once you have accepted a theory and used it as a tool in your thinking, it is extraordinarily difficult to notice its flaws. If you come upon an observation that does not seem to fit the model, you assume that there must be a perfectly good explanation that you are somehow missing. You give the theory the benefit of the doubt, trusting the community of experts who have accepted it.
(From Thinking Fast and Slow)
In other words, I think that trusting existing theories too much is a very general mistake that lots of people make in lots of contexts.
Yes! I was thinking about adding a couple paragraphs about this, but couldn't figure out how to word it quite right.
When you're trying to create solid theories de-novo, a huge part of it is finding people who've done a bunch of experiments with it, looking at the outcomes, and paying really close attention to the places where they don't match your existing theory. Elinor Ostrom is one of the best examples I know: she won a Nobel in economics for basically saying "ok, how do people actually solve commons problems in practice, and does it make sense from an economic perspective?"
In the case of a wheel with weights on it, that's been nailed down really well already by generations of physicists, so it's not a very good example for theory-generation.
But one important aspect does carry over: you have to actually do the math, to see what the theory actually predicts. Otherwise, you won't notice when the experimental outcomes don't match, so you won't know that the theory is incomplete.
Even in the wheel example, I'd bet a lot of physics-savvy people would just start from "oh, all that matters here is moment of inertia", without realizing that it's possible to shift the initial gravitational potential. But if you try a few random configurations, and actually calculate how fast you expect them to go, then you'll notice very quickly that the theory is incomplete.
To the extend that this is true, our scientific system should move in a direction where data is written up in a way that allows lay people that aren't exposed the theory of a field can interact with it.
It's baby steps, but CERN has an open data portal, where you can download raw data from their LHC experiments for your own analysis. The portal also includes the software used to conduct the analysis, so you don't have to write your own code to process terabytes of LHC collision data.
I would guess that high energy physics is a field where laypeople might make a lot less process then biology or psychology, so I would be more interested in data sets in those domains.
A relevant experience: We spent a good few months tackling a motor problem where our calculations showed we should have been fine. In the end it turned out that someone had entered an incorrect input in one calculation and the test was far too harsh. All the time when we were having the problem the test engineers (read “people who have done a lot of iterative optimisation”) were saying it seemed like the test was too harsh. We wasted months trusting too much in the calculations. Sometimes the main uncertainty is that your model is wrong (or just inadequate) in which case iterative optimisation might win.
Well… not necessarily. We’re talking here about a wheel, with weights on it, rolling down a ramp. Mathematically, this system just isn’t all that complicated. Anyone with an undergrad-level understanding of mechanics can just crank the math, in all of its glory. Take no shortcuts, double-check any approximations, do it right. It’d be tedious, but certainly not intractable. And then… then you’d understand the system.
I guess the idea was to emulate a problem without a established theory, and it was chosen to provide a simple setup for changing the parameters and visualizing the results.
Imagine that instead of this physics problem it was like Eliezer Yudkowsky's problem to find the rule that explain a sequence of numbers, where you cannot find someone who already developed a solution for it. It is easier to generate a set of numbers that satisfies the rule (similar to the iterative optimization) than the rule/theory itself, as each of those proposed rules are falsified by the next iterations.
If it was modified to generate an output to be maximized instead of a true/false answer, the iterative optimization would get a good result faster, but not the optimal solution. If you played this game several times, the optimizers would probably get good heuristic to find a good solution, while the theorizers might find a meta-solution that solves all the games.
For me it looks like that if that experiment was extended to more iterations (and maybe some different configurations of communication between each generation and between independent groups) you would get a simple model of how science progress. Theory pays in the long term, but it might be hindered if the scientist refuse to abandon their proposed/inherited solution.
Thank you for writing this. Since most of my effort involves developing and iterating on ad-hoc incomplete theories, this is extremely relevant.
I'm curious how the complexity of the system affects the results. If someone hasn't learned at least a little physics - a couple college classes' worth or the equivalent - then the probability of inventing/discovering enough of the principles of Newtonian mechanics to apply them to a multi-parameter mechanical system in a few hours/days is ~0. Any theory of mechanics developed from scratch in such a short period will be terrible and fail to generalize as soon as the system changes a little bit.
But what about solving a simpler problem? Something non-trivial but purely geometric or symbolic or something for which a complete theory could realistically be developed by a group of people passing down data and speculation through several rounds of tests. Is it still true that the blind optimizers outperform the theorizers?
What I'm getting at is that this study seems to point to a really interesting and useful limitation to "amateur" theorizing, but if the system under study is sufficiently complicated, it becomes easy to explain the results with the less interesting, less useful claim that a group of non-specialists will not, in a matter of hours or days, come up with a theory that required a community of specialists years to come up with.
For instance, a bunch of undergrads in a psych study are not going to rederive general relativity to improve the chances of predicting when pictures of stars look distorted - clearly in that case the random optimizers will do better but this tells us little about the expected success of amateur theorizing in less ridiculously complicated domains.
Sometimes theory can open up possibilities rather than closing them off. In these cases, once you have a theory that claims that X is important, then you can explore different values of X and do local hill-climbing. But before that it is difficult to explore by varying X, either because there are too many dimensions or because there is some subtlety in recognizing that X is a dimension and being able to vary its level.
This depends on being able to have and use a theory without believing it.
performance was improving, but understanding was not.
If they were passing on data, couldn't they reference the data for 'predictions'?
An interesting experiment: researchers set up a wheel on a ramp with adjustable weights. Participants in the experiment then adjust the weights to try and make the wheel roll down the ramp as quickly as possible. The participants go one after the other, each with a limited number of attempts, each passing their data and/or theories to the next person in line, with the goal of maximizing the speed at the end. As information accumulates “from generation to generation”, wheel speeds improve.
This produced not just one but two interesting results.
First, after each participant’s turn, the researchers asked the participant to predict how fast various configurations would roll. Even though wheel speed increased from person to person, as data accumulated, their ability to predict how different configurations behave did not increase. In other words, performance was improving, but understanding was not.
Second, participants in some groups were allowed to pass along both data and theories to their successors, while participants in other groups were only allowed to pass along data. Turns out, the data-only groups performed better. Why? The authors answer:
And:
So, two lessons:
So… we should iteratively optimize and forget about theorizing? Fox not hedgehog, and all that?
Well… not necessarily. We’re talking here about a wheel, with weights on it, rolling down a ramp. Mathematically, this system just isn’t all that complicated. Anyone with an undergrad-level understanding of mechanics can just crank the math, in all of its glory. Take no shortcuts, double-check any approximations, do it right. It’d be tedious, but certainly not intractable. And then… then you’d understand the system.
What benefit would all this theory yield? Well, you could predict how different configurations would perform. You could say for sure whether you had found the best solution, or whether better configurations were still out there. You could avoid getting stuck in local optima. Y’know, all the usual benefits of actually understanding a system.
But clearly, the large majority of participants in the experiment did not crank all that math. They passed along ad-hoc, incomplete theories which didn’t account for all the important aspects of the system.
This suggests a valley of bad theory. People with no theory, who just iteratively optimize, can do all right - they may not really understand it, they may have to start from scratch if the system changes in some important way, but they can optimize reasonably well within the confines of the problem. On the other end, if you crank all the math, you can go straight to the optimal solution, and you can predict in advance how changes will affect the system.
But in between those extremes, there’s a whole lot of people who are really bad at physics and/or math and/or theorizing. Those people would be better off just abandoning their theories, and sticking with dumb iterative optimization.