X explains Z% of the variance in Y
27foodforthought
4Leon Lang
6foodforthought
2Leon Lang
3Stepan
14habryka
12pmarc
11foodforthought
1pmarc
2Leon Lang
10rain8dome9
9[anonymous]
7the gears to ascension
1rain8dome9
3Leon Lang
3Leon Lang
3Ŧhomas
2Leon Lang
9Stepan
2Leon Lang
8Neel Nanda
5Causal Chain
5Sheikh Abdur Raheem Ali
4quiet_NaN
1homosapien97
4Midi
4Leon Lang
1Midi
3Stepan
3rotatingpaguro
7Leon Lang
4Dalcy
2Leon Lang
3rotatingpaguro
New Comment
TL;DR: Information Theory is another mathematical framework for understanding the relatedness of X and Y based on measured joint probability distributions.
Epistemic status - quite confident. I would not be qualified to teach a course on this for graduate students in mathematics or statistics, but I do teach a course on this for PhD students in biology and psychology.
Well done! In the spirit of "yes, and", I think it is worth pointing out that there are highly related concepts in Shannon Information Theory, and wonder if this comes closer to the OP's notion of Platonic Variance Explained. (If there's interest in a longer explanation of Info. Theory with equations and graphs and examples, I could write that as a post; but perhaps that's already well-tread ground here. For now I just want to make a quick comparison, without fully fleshing out the points).
In the "explained variance" framework we think about the variability of possible Y's in terms of its spread around (literally, distance from) the mean value of Y. If you don't know what Y is in a particular case and you are forced to guess, often the average Y is a good guess in two senses: first, on average this guess has the lowest error (squared difference between the guess and the actual value of Y); and second, it is more frequently correct than any other choice. But this is predicated on the implicit model that Y is a normally distributed variable. Due to the Central Limit Theorem, many variables are approximately normally distributed, so this model is often a useful one. Regression then builds on this to quantify the extent to which X constrains the possible value of Y, as nicely explained above. The OP nicely explains that "variance explained" means the extent to which some particular model of Y based on X (such as: Y=mX+b), provides a better guess than the alternative model of Y=the average Y in the first sense mentioned above. This statement is at least as much a statement about the model, as about X.
Information Theory measures the same things from the same data, through a different conceptual lens.
Instead of measuring the variability of Y by its variance, Information Theory measures this by its entropy, which you can think of is the uncertainty you have about Y before you observe it. Like the variance, the entropy only depends on the distribution of Y. But unlike variance, entropy makes no assumptions about the shape of the distribution of Y. The values of Y can have an arbitrarily complex, non-parametric distribution, for which the mean value of Y might be an extremely bad guess in both senses mentioned above.
Instead of measuring the relationship between X and Y by the variance explained, Information Theory measures the mutual information between X and Y, which you can think of as how much your uncertainty about Y is reduced by knowing X. Like "variance explained", mutual information depends only on the joint distribution of X and Y. But unlike regression, it does not require positing any model of how Y depends on X. This is powerful, because it gives you a fact about the X-Y relationship, not a fact about the goodness of some model. You can measure mutual information even if the form of the relationship is unknown or complicated. On the down side, since it's model-free, it doesn't directly give you a method for predicting Y from X.
I think Mutual Information comes closer to what the OP calls the Platonic Variance Explained, but correct me if I'm wrong!
I'm restricting myself to the main theme of the OP here, but it might be interesting flesh out other ways the two frameworks are similar or different, such as issues of under-sampling/overfitting, independence-of-samples assumption; correlation vs causation; data processing inequality...
Thanks for the comment! Actually, after writing the post, I also wondered why this concept isn't based on information theory :) I think what I'd enjoy most, if you wanted to write it, is probably an in-depth treatment of the differences in meaning, properties, and purpose of:
- Entropy vs. variance
- Mutual information vs. variance explained
- conditional entropy vs. average remaining variance
- etc.
But unlike variance explained, it does not require positing any model of how Y depends on X. This is powerful, because it gives you a fact about the X-Y relationship, not a fact about the goodness of some model.
Note that parts of my post are actually model-free! For example, the mathematical definition and the example of twin studies do not make use of a model.
But this is predicated on the implicit model that Y is a normally distributed variable.
I'm not aware of (implicitly) making that assumption in my post!
You can measure mutual information even if the form of the relationship is unknown or complicated.
Is this so? Suppose we'd want to measure differential entropy, as a simplified example, and the true density "oscillates" a lot. In that case, I'd expect that the entropy is different than what it is if the density were smoother. But it might be hard to see the difference in a small dataset. The type of regularity/simplicity assumptions about the density might thus influence the result.
Note that parts of my post are actually model-free! For example, the mathematical definition and the example of twin studies do not make use of a model
Yes, good point, I should have said "unlike regression" rather than "unlike variance explained". I'll have to think more on how the type of analysis described in the twin example maps onto information theory.
But this is predicated on the implicit model that Y is a normally distributed variable.
I'm not aware of (implicitly) making that assumption in my post!
By "this" I meant the immediately preceding statements in my post. (Although the cartoon distributions you show do look normal-ish, so at least you invite that intuition). The idea that the mean or average is a good measure of central tendency of a distribution, or a good estimator, is so familiar we forget that it requires justification. For Normal distributions, it is the lowest MSE estimator, the maximum likelihood estimator, and is an unbiased estimator, but this isn't true of all distributions. For a skewed, long-tailed distribution, for example, the median is a better estimator. For a binomial distribution, the mean is almost never the maximum likelihood estimator. For a Cauchy distribution, the mean is not even defined (although to be fair I'm not entirely sure entropy is well defined in that case, either). Likewise the properties of variance that make it a good estimator of dispersion for a Normal distribution don't necessarily make it good for other distributions.
It is true that partitioning of variance and "variance explained" as such don't rely on a normality assumption, and there are non-parametric versions of regression, correlation, ANOVA etc. that don't assume normality. So I have not entirely put my finger on what the difference is.
You can measure mutual information even if the form of the relationship is unknown or complicated.
Is this so? Suppose we'd want to measure differential entropy, as a simplified example, and the true density "oscillates" a lot. In that case, I'd expect that the entropy is different than what it is if the density were smoother. But it might be hard to see the difference in a small dataset. The type of regularity/simplicity assumptions about the density might thus influence the result.
This might be a good place to mention that I work exclusively with discrete entropy, and am not very familiar with notations or proofs in differential (continuous) entropy. So if Y is continuous, in practice this involves discretizing the value of Y (binning your histograms). I agree the continuous case would be more directly comparable, but I don't think this is likely to be fundamentally important, do you?
In principle, conceptually, you can estimate entropy directly from the probability density function (PDF) non-parametrically as H = sum(-P log2 P), where the sum is over all possible values of Y, and P is the probability Y takes on a given value.[1] Likewise, you can estimate the mutual information directly from the joint probability distribution between X and Y, the equation for which I won't try to write out here without an equation editor. In practice, if Y is continuous, the more data you have, the more finely you can discretize Y and the more subtly you can describe the shape of the distribution, so you converge on the true PDF and thus the true entropy as the data size goes to infinity.
I'm not denying that it can take a lot of data to measure entropy or mutual information by brute force in this way. What is worse, these naive estimators are biased if distributions are under-sampled. So getting a good estimate of entropy or mutual information from data is very tricky, and the shape of the distribution can make the estimation more or less tricky. To the extent one relies on regularity or simplicity assumptions to overcome data limitations, these assumptions can affect your result.
Still, if you are careful about it, an estimate based on assumptions can still be a strict bound: X removes at least z% of your uncertainty about Y. There is a direct analogy in regression models: if Yhat=f(X) explains z% of the variance of y (assuming this is established properly), then x "Platonically" explains at least z% of the variance of y.
Relatedly, you can pre-process X into some derived variable such as Q=f(X) or an estimator Yhat=f(X), and then measure the mutual information between the derived variable and the true value of Y. The Data Processing Inequality states that if the derived variable contains Z amount of information about Y, the input variable X must contain at least that much information. This is very much like defining a particular regression model f(X); and in the Yhat=f(X) case, it does give you a model you can use to predict Y from X.
- ^
sorry, I haven't figured out the equation editor yet.
The idea that the mean or average is a good measure of central tendency of a distribution, or a good estimator, is so familiar we forget that it requires justification. For Normal distributions, it is the lowest MSE estimator, the maximum likelihood estimator, and is an unbiased estimator, but this isn't true of all distributions. For a skewed, long-tailed distribution, for example, the median is a better estimator.
Is it correct to say that the mean is a good estimator whenever the variance is finite? If so, maybe I should have added that assumption to the post.
I wonder how to think about that in the case of entropy, which you thought about analyzing. Differential entropy can also be infinite, for example. But the Cauchy distribution, which you mention, has infinite variance but finite differential entropy, at least.
1.sorry, I haven't figured out the equation editor yet.
You can type Cmd+4 to type inline latex formulas, and Cmd+m to type standalone latex formulas! Hope that helps.
In principle, conceptually, you can estimate entropy directly from the probability density function (PDF) non-parametrically as H = sum(-P log2 P), where the sum is over all possible values of Y, and P is the probability Y takes on a given value. Likewise, you can estimate the mutual information directly from the joint probability distribution between X and Y, the equation for which I won't try to write out here without an equation editor.
Note: After writing the next paragraph, I noticed that you made essentially the same points further below in your answer, but I'm still keeping my paragraph here for completeness.
I was more wondering whether we can estimate them from data, where we don't get the ground-truth values for the probabilities that appear in the formulas for entropy and mutual information, at least not directly. If we have lots of data, then we can approximate a PDF, that is true, but I'm not aware of a way of doing so that is entirely principles or works without regularity assumptions. As an example, let's say we want to estimate the conditional entropy (a replacement for the "remaining variance" in my post) for continuous and . I think in this case, if all sampled -values differ from each other, you could in principle come to the conclusion that there is no uncertainty in conditional on at all since you observe only one -value for each -value. But that would be severe overfitting, similar to what you'd expect in my section titled "When you have lots of data" for continuous .
Maybe it would be interesting to analyze the conditional entropy case for non-continuous distributions where variance makes less sense.
I think from my point of view we're largely in agreement, thanks for your further elaborations!
Is it correct to say that the mean is a good estimator whenever the variance is finite?
Well, yes, in the sense that the law of large numbers applies, i.e.
The condition for that to hold is actually weaker. If all the are not only drawn from the same distribution, but are also independent, the existence of a finite is necessary and sufficient for the sample mean to converge in probability to as goes to infinity, if I understand the theorem correctly (I can't prove that yet though; the proof with a finite variance is easy). If aren't independent, the necessary condition is still weaker than the finite variance, but it's cumbersome and impractical, so finite variance is fine I guess.
But that kind of isn't enough to always justify the use of a sample mean as an estimator in practice? As foodforthought says, for a normal distribution it's simultaneously the lowest MSE estimator, the maximum likelihood estimator, and is an unbiased estimator, but that's not true for other distributions.
A quick example: suppose we want to determine the parameter of a Bernoulli random variable, i.e. "a coin". The prior distribution over is uniform; we flip the coin times, and use the sample success rate, , i.e. the mean, i.e. the maximum likelihood estimate. Per simulation the mean squared error is about 0.0167. However, if we use instead, the mean squared error drops to 0.0139 (code).
Honestly though, all of this seems like frequentist cockamamie to me. We can't escape prior distributions; we may as well stop pretending that they don't exist. Just calculate a posterior and do whatever you want with it. E.g., how did I come up with the example? Well, it's the expected value of the posterior beta distribution for if the prior is uniform, so it also gives a lower MSE.
I find the phrase this post is about extremely useful. I've also had thoughts along very similar lines in terms of how to define it. And indeed, upon searching the internet I have found no similarly good reference for what this phrase means as this post and the comments below it. As such, it seems to me to be providing a very valuable service of defining and clarifying an expression widely in use.
In my opinion, this post misses the main challenge with the "platonic ideal" vision of a concept like % of explained variance: it's something that accidentally depends on the distribution of your variables in the sample, rather than a fundamental property of the relationship between those variables.
The total variance Var(Y) depends on the distribution of not only X, but all variables affecting Y. Also, because in general Var(Y|X) can depend on X, the term in the definition, which is really the average of Var(Y|X) across all X, depends on the distribution of X.
So from my understanding and in my practical experience using statistics, the coefficient of determination (what % of variance of Y is explained by X) always provides "narrow" information tailored to a specific context, not general information about a platonic ideal understanding of the relationship between X and Y. [I understand it might appear a bit defeatist relative to the goal set by OP... personally I have found accepting that has been useful to avoid a lot of unproductive arguments in real world cases.]
Heritability is a classic example. It can be useful in the context of e.g. breeding crops in specific conditions and predicting how much selection on a trait will affect the next generation, but the heritability you get overestimates how much genetics affect variance in the wild, where the environment is much more variable. Also, since there are genetics x environment interactions, Var(phenotype|genotype) estimated from a limited range of environments is not a good estimate of the average Var(phenotype|genotype) globally.
In the context of twins studies, if you think of twins raised together (as they would be in most cases), then the "predictors" that they share and that could influence whatever outcome you're measuring include a lot more than just genes. So if you're comparing twins vs. non-twins siblings, you overestimate the genetic portion of heritability of the characteristic of interest, since all your comparisons are based on a greater shared environment that 2 random people in the population.
--
As a sidenote, this is a compromise that occurs a lot in study design: if you need to estimate the relationship between Y and X, it's actually useful to have a population that varies less by factors other than X, but doing so potentially limits the generalization of the results to the broader population. If you want a broader sample so your conclusions are more likely to apply in different contexts, you may need a very large sample size, because in effect you need to calculate conditional distributions of (Y|X) for all sorts of combinations of the other variables.
---
Lastly, even if somehow you were able to calculate a version of "% of human characteristic that's genetically explained", that would be the true average across all populations / cultures / etc., you get the problem that the underlying distributions are not fixed in time. In my view, an answer that's contingent of very specific distribution of cultural practices / human environments available at this moment is not a very fundamental quantity of interest, it's more like an accidental characteristic as I mention above.
In my opinion, this post misses the main challenge with the "platonic ideal" vision of a concept like percentage of explained variance: it's something that accidentally depends on the distribution of your variables in the sample, rather than a fundamental property of the relationship between those variables.
Perhaps we need to step back and clarify what "Platonic Explained Variance" could even mean. All knowledge is contextual; it is a mistake to expect that there is a Truth to be known devoid of context. I supposed that the OP meant by this phrase something like: the true, complete statistical dependence between X and Y in the sampled population, as against our estimate or approximation of that dependence based on a given limited sample or statistical model. In any case, I'd like to argue that such distinction makes sense, while it does not make sense to look for a statistical relationship between X and Y that is eternally and universally true, independent of a specific population.
When we are using empirical statistics to describe the relationship between measurable variables X and Y, I think the conclusions we draw are always limited to the population we sampled. That is the essential nature of the inference. Generalization to the sampled population as a whole carries some uncertainty, which we can quantify based on the size of the sample we used and the amount of variability we observed, subject to some assumptions (e.g., about the underlying distributions, or independence of our observations).
But generalization to any other population always entails additional assumptions. If the original sample was limited in scope (e.g. a particular age, sex, geographic location, time point, or subculture), generalization outside that scope entails a new conjecture that the new group is essentially the same as the original one in every respect relevant to the claim. To the extent the original sample was broad in scope, we can as you say test whether such other factors detectably modified the association between X and Y, and if so, include these effects as covariates in our statistical model. As you note, this requires a lot of statistical power. Even so, whenever we generalize outside that population, we assume the new population is similar in the ways that matter, for both the main association and the modifier effects.
A statistical association can be factually, reproducibly true of a population and still be purely accidental, in which case we don't expect it to generalize. When we generalize to a new context or group or point in time, I think we are usually relying on an (implicit or explicit) model that the observed statistical relation between X and Y is a consequence of underlying causal mechanisms. If and to the extent that we know what causal mechanisms are at play, we have a basis for predicting or checking whether the relevant conditions apply in any new context. But (1) generalization of the causal mechanism to a new condition is still subject to verification; a causal model derived in a narrow context could be incomplete, and the new condition may differ in a way that turns out to be causally important in a way we didn't suspect; and (2) even if the causal mechanism perfectly generalizes, we do not expect "the fraction of variance explained" to generalize universally. That value depends on a plethora of other random and causal factors that will in general be different between populations [^1].
Summing up, I think it's a mistake to look for the 'Platonic Variance Explained' divorced from a specific population. But we can meaningfully ask if the statistical dependence we estimated from a finite empirical sample using a particular statistical model accurately reflects the true and complete statistical dependence between the variables in the population from which we sampled.
- This account might be particular to the branches of natural science that seek mechanistic causal models and/or fundamental theories as explanations. Other fields of research or philosophic frameworks that lack or eschew causal explanation or theory may have a different epistemic account, which I'd be interested to hear about.
Yes, when trying to reuse the OP's phrasing, maybe I wasn't specific enough on what I meant. I wanted to highlight how the "fraction of variance explained" metric generalized less that other outputs from the same model.
For example, if you conceive a case where a model of E[y] vs. x provides good out-of-sample predictions even if the distribution of x changes, e.g. because x stays in the range used to fit the model, the fraction of variance explained is nevertheless sensitive to the distribution of x. Of course, you can have a confounder w that makes y(x) less accurate out-of-sample because its distribution changes and indirectly "breaks" the learned y(x) relationship, but then, w would influence the fraction of variance explained even if it's not a confounder, even if it doesn't break the validity of y(x).
Or for a more concrete example, maybe some nutrients (e.g. Vitamin C) are not as predictive of individual health as they were in the past, because most people just have enough of them in their diet, but fundamentally the relationship between those nutrients and health hasn't changed, just the distribution; our model of that relationship is probably still good. This is a very simple example. Still, I think in general there is a lot of potential misinterpretation of this metric (not necessarily on this forum, but in public discourse broadly), especially as it is sometimes called a measure of variable importance. When I read the first part of this post about teachers from Scott Alexander: https://www.lesswrong.com/posts/K9aLcuxAPyf5jGyFX/teachers-much-more-than-you-wanted-to-know , I can't conclude from "having different teachers explains 10% of the variance in test scores" that teaching quality doesn't have much impact on the outcome. (And in fact, as a parent I would value teaching quality, but not a high variance in teaching quality within the school district. I wouldn't want my kids learning of core topics to be strongly dependent of which school or which class in that school they are attending.)
Thanks, I think this is an excellent comment that gives lots of useful context.
To summarize briefly what foorforthought has already expressed, what I meant with platoninc variance explained is the explained variance independent of a specific sample or statistical model, but as you rightly point out, this still depends on lots of context that depends on crucial details of study design or the population one studies.
random variables
This term always sounds like it means a variable selected at random not a variable with randomness in it. Please use the term 'stochastic variable'. Edit: or does it mean a variable composed entirely at random without any relation to any other variable?
Edit: I think this post would be much easier to learn from if it was a jupyter notebook with python code intermixed or R markdown. Sometimes the terminology gets away from me and seeing in code what is being said would really help understand what is going on as well as give some training on how to use this knowledge. Edit: there should be a plot illustrating " which are jointly sampled according to a density ." including rugs for the marginal distributions. I could do that if anyone wants. Here is an example describing a different concept.
Unfortunately, this is a well-established mathematical term that's used universally throughout probability theory. Changing notation to match intuition is not feasible; we must instead change intuition to match notation.
Technically speaking, a random variable is just a measurable function , where is the underlying sample space and is some measurable space. Indeed, even if the function is constant, it is technically speaking still a random variable (in this case it's called a deterministic random variable).
The problem is that, in practice, people don't really pay too much attention to precisely what the sample space is, especially if they don't have some specific reason to care about measure theory. They instead often want to talk about the probability distribution, and the task of figuring out formally and rigorously why this is all well-defined is often omitted. Luckily, the Kolmogorov extension theorem and related results usually allow you to pick a "large enough" sample space that carries all the content you need for your math work.
https://en.wikipedia.org/wiki/Random_variable
stochastic variable is certainly less common, but googling it only returns the right thing. it seems like it'd be a valid replacement and I agree it could reduce a common confusion.
"Random variable" is never defined. I though stochastic variable is just a synonym for random variable. I have seen posts where random variable is always written as r.v. and that helps a bit.
From Wikipedia: "In probability theory, the sample space (also called sample description space,[1] possibility space,[2] or outcome space[3]) of an experiment or random trial is the set of all possible outcomes or results of that experiment.
what is a measurable space?
"he function is constant," you mean its just one outcome like a die that always lands on one side?
what makes a function measurable?
what is a measurable space?
I'm not sure if clarifying this is most useful for the purpose of understanding this post specifically, but for what it's worth: A measurable space is a set together with a set of subsets that are called "measurable". Those measurable sets are the sets to which we can then assign probabilities once we have a probability measure (which in the post we assume to be derived from a density , see my other comment under your original comment).
"the function is constant," you mean its just one outcome like a die that always lands on one side?
I think that's what the commenter you replied to means, yes. (They don't seem to be active anymore)
what makes a function measurable?
This is another technicality that might not be too useful to think about for the purpose of this post. A function is measurable if the preimages of all measurable sets are measurable. I.e.: , for two measurable spaces and , is measurable, if is measurable for all measurable . For practical purposes, you can think of continuous functions or, in the discrete case, just any functions.
I'm sorry that the terminology of random variables caused confusion!
If it helps, you can basically ignore the formalism of random variables and instead simply talk about the probability of certain events. For a random variable with values in and density , an event is (up to technicalities that you shouldn't care about) any subset . Its probability is given by the integral
In the case that is discrete and not continuous (e.g., in the case that it is the set of all possible human DNA sequences), one would take a sum instead of an integral:
The connection to reality is that if we sample from the random variable , then its probability of being in the event is modeled as being precisely . I think with these definitions, it should be possible to read the post again without getting into the technicalities of what a random variable is.
I think this post would be much easier to learn from if it was a jupyter notebook with python code intermixed or R markdown.
In the end of the article I link to this piece of code of how to do the twin study analysis. I hope that's somewhat helpful.
FYI Likelihood refers to a function of parameters given the observed data.
Likelihood being larger supports a particular choice of parameter estimate, ergo one may write some hypothesis is likely (in response to the observation of one or more events).
The likelihood of a hypothesis is distinct from the probability of a hypothesis under both bayesianism and frequentism.
Likelihood is not a probability: it does not integrate to unity over the parameter space, and scaling it up to a monotonic transformation does not change its usage or meaning.
I digress, the main point is there is no such thing as the likelihood of an event. Again, Likelihood is a function of the parameter viz. the hypothesis. Every hypothesis has a likelihood (and a probability, presuming you are a bayesian). Every event has a probability, but not a likelihood.
Thanks, I've replaced the word "likelihood" by "probability" in the comment above and in the post itself!
It really is an important, well-written post, and I very much enjoyed it. I especially appreciate the twin studies example. I even think that something like that should maybe go into the wikitags, because of how often the title sentence appears everywhere? I'm relatively new to LessWrong though, so I'm not sure about the posts/wikitags distinction, maybe that's not how it's done here.
I have a pitch for how to make it even better though. I think the part about "when you have lots of data" vs "when you have less data" would be cleaner and more intuitive if it were rewritten as "when is discrete vs continuous". Now the first example (the "more data" one) uses a continuous ; thus, the sentence "define as the sample mean of taken over all for which " creates confusion, since it's literally impossible to get the same value from a truly continuous random variable twice; it requires some sort of binning or something, which, yes, you do explain later. So it doesn't really flow as a "when you have lots of data" case---nobody does that in practice with continuous , no matter how much data (at least as far as I know).
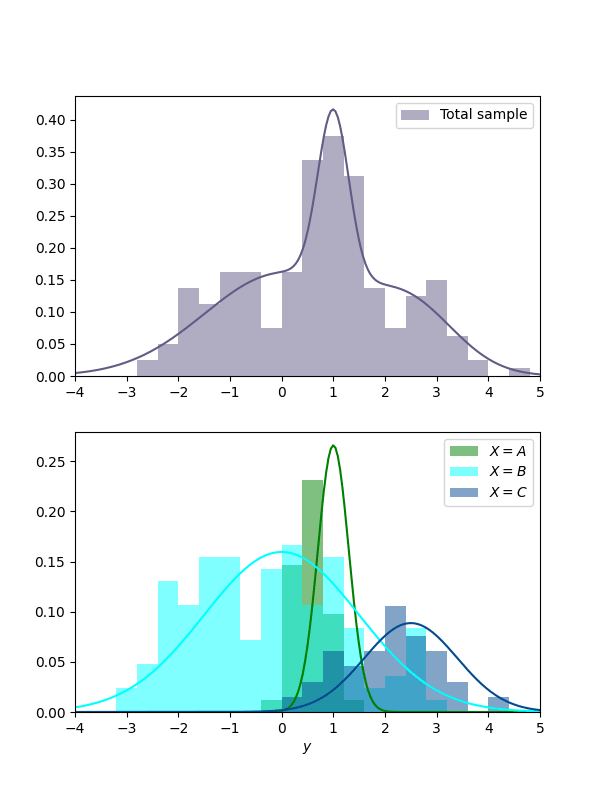
Now say we have a discrete : e.g., an observation can come from classes A, B, or C. We have a total of observations, from class . Turning the main spiel into numbers becomes straightforward:
On average, over all different values of weighted by their probability, the remaining variance in is times the total variance in .
- "Over all different values of " -> which we have three of;
- "weighted by their probability" -> we approximate the true probability of belonging to class as , obviously;
- "the remaining variance in " for class is , also obviously.
And we are done, no excuses or caveats needed! The final formula becomes:
An example: . Since we are creating the model, we know the true "platonic" explained variance. In this example, it's about 0.386. An estimated explained variance on an sample came out as 0.345 (code)
After that, we can say that directly approximating the variance of for every value of a continuous is impossible, so we need a regression model.
And also that way it prepares the reader for the twin study example, which then can be introduced as a discrete case with each "class" being a unique set of genes, where always equals two.
If you do decide that it's a good idea, but don't feel like rewriting it, I guess we can go colab on the post and I can write that part. Anyway, please let me know your thoughts if you feel like it.
Thanks for the comment Stepan!
I think it's right that the distinction "lots of data" and "less data" doesn't really carve reality at its natural joints. I feel like your distinction between "discrete" and "continuous" also doesn't fully do this since you could imagine a case of discrete where we have only one for each in the dataset, and thus need regression, too (at least, in principle).
I think the real distinction is probably whether we have "several 's for each " in the dataset, or not. The twin dataset case has that, and so even though it's not a lot of data (only 32 pairs, or 64 total samples), we can essentially apply what I called the "lots of data" case.
Now, I have to admit that by this point I'm somewhat attached to the imperfect state of this post and won't edit it anymore. But I've strongly upvoted your comment and weakly agreed with it, and I hope some confused readers will find it.
Nice post. The intuition that makes most sense to me is "how much less uncertain/confused should I be about Y, on average, if I know the value of X"
The relevant intuition I use comes from the [law of total variance](https://en.m.wikipedia.org/wiki/Law_of_total_variance) (or variance decomposition formula):
An interpretation: if you sample Y through a process of getting partial information step by step, the variance of each step adds up to the variance of sampling Y directly
The first two terms are V_{tot}(Y) and E[Var_{rem}(Y|X)] respectively, while the last part describes the "explained" variance.
To give an intuition for Var(E[Y|X]):
- If X gives me some information about Y, then my new mean for Y should change depending on X. If X gives little information, then it should only wiggle my mean estimate of Y a little (low variance), but a very explanatory X will move my mean estimate of Y a lot (high variance)
- If X gave no information, then E[Y|X] should have no variance (it's always equal to the mean E[Y]).
- If X completely explains Y, then E[Y|X] can equal any value in the domain of Y. Because every y has a corresponding x, that if sampled, means that P(Y=y|X=x) = 1. Indeed, E[Y|X] will have exactly the same distribution as Y, and so it will contain the full variance as Y
Thanks for writing this up. I really appreciate this post because I was confused about the intuition behind variance explained despite this being the primary evaluation metric used in a recent paper I co-authored on interpreting text-to-image diffusion models with dictionary learning. It's more helpful than any other resource I used.
While I am fine with your math, I do not like the phrasing "X explains Z% of the variance of Y", because to the casual reader, it suggests that there is a causal relationship. For example, I might say "smoking explains X% of the (variance of the binary variable indicating the presence of) lung cancer (cases)". Here I have a causal relationship.
But consider "IQ explains X% of the variance of lifetime earnings in Americans", or "Lifetime earnings explain Y% of the IQ variance in Americans". The casual reader might read the first sentence and infer a causal relationship. "Every point of IQ I CRISPR into my kid will raise the expected amount of money they make by $Z". But purely from the correlation, we can not be sure that this intervention will have any effect at all (though there are good reasons to believe that there is some causal relationship).
More bluntly, getting a positive result on a cancer screening is correlated with dying in the next decade, but bribing your doctor to falsify your results has the opposite effect on your life expectancy as you would guess from the correlation.
Scott Alexander has recently written about heritability:
Predictive power is different from causal efficacy. Consider a racist society where the government ensures that all white people get rich but all black people stay poor. In this society, the gene for lactose tolerance (which most white people have, but most black people lack) would do a great job predicting social class, but it wouldn’t cause social class.
(As usual, worth reading in full.)
Or take your initial statement
The group consensus on somebody's attractiveness accounted for roughly 60% of the variance in people's perceptions of the person's relative attractiveness.
There could be vastly different causal models which explain this observation:
a) Every group member randomly assigns an attractiveness rating to a newcomer. Then everyone signals the attractiveness rating they assigned implicitly or explicitly through group interactions, and every group member updates towards the group consensus.
b) The group has some rough consensus about which traits are attractive (perhaps there is an universal attractiveness, or the group members adjusted their preferences to the group average over time, or people who find certain traits attractive ended in the group for complicated reasons), so they will rate a newcomer similarly based on their traits.
Likely, in reality it is going to be a mix of both of these and also three more causal chains. Again, as soon as you are discussing interventions you will find "explains X% of the variance" insufficient. Say you want to ask a specific person of that group on a date. You know that the group generally likes people with stripy socks, but that your potential date is indifferent to them. In case (a), you want to wear stripy socks because the group consensus of your attractiveness will update the attractiveness rating of your potential date, while in case (b) it does not matter.
I agree that "X explains Q% of the variance in Y" to me sounds like an assertion of causality, and a definition of that phrase that is merely correlations seems misleading.
Might it be better to say "After controlling for Y, the variance of X is reduced by Q%" if one does not want to imply causation?
Nice post. Is there some subtle distinction between and I'm missing, or are they synonyms as used here?
They are synonyms! Both are the expected value of (the function of) a random variable. (I had started writing mu, but then changed the notation for the remaining variance to also make the expected value explicit as requested. Mu seemed like less appropriate notation for this. Maybe I’ll change all mu to E once I have access to more than my phone again. Edit: I was too lazy to do that change :) ).
Consequently, we obtain
Technically, we should also apply Bessel's correction to the denominator, so the right-hand side should be multiplied by a factor of . Which is negligible for any sensible , so doesn't really matter I guess.
I don't like the notation because appears as a free RV but actually it's averaged over. I think it would be better to write .