I argued in this post that the differences in capability between different researchers are vast (Kaj Sotala provided me with some interesting empirical evidence that backs up this claim). Einstein's contributions to physics or John von Neumann's contributions to mathematics (and a number of other disciplines) are arguably at least hundreds of times greater than that of an average physicist or mathematician.
At the same time, Yudkowsky argues that "in the space of brain designs" the difference between the village idiot and Einstein is tiny. Their brains are extremely similar, with the exception of some "minor genetic tweaks". Hence we get the following picture:

The picture I am painting is rather something like this:

It would seem that these pictures are incompatible - something that would be a problem for my picture, since I think that Yudkowsky's picture is right. So how can they both be true? The answer is, obviously, that they are measuring different things. The first is measuring something like difference in brain design that is relevant for intelligence. The second is rather measuring the difference in capability to come up with physical theories that are of use for mankind. Here the village idiot is on par with the chimp and the mouse - all of whom have no such capability whatsover. The average physicist has some such capability, but it's just a fraction of Einstein's.
Why is this? Well it is not because the village idiot has no capability at all to come up with physical theories. In fact, a primitive physical theory that is quite useful is hard-wired into our brains. Rather, the reason is that the village idiot has no capability to come up with a physical theory that is not already well-known.
Problems in theoretical physics and mathematics are typically problems that are so complex that they are hard to solve for some of the world's smartest people. This means that unless you're quite smart, your chances of contributing anything at at all to these disciplines is very slim. But, if you are but a tiny bit smarter than everyone else, you'll be able to spot solutions to problem after problem that others have struggled with - these problems being problems precisely because they were hard to solve for people with a certain level of intelligence. Thus we get something like the following relationship between cognitive ability, in Yudkowsky's sense, and ability to come up with useful physical theories, i.e. productivity - what I'm talking about:
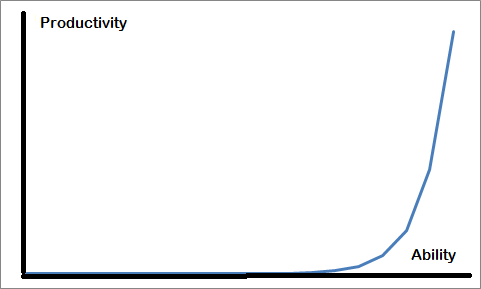
It is for this reason that people like von Neumann and Einstein are so vastly much more productive than the average mathematician/physicist. The difference in intelligence is tiny on Yudkowsky's scale - obviously much smaller than that between Einstein and the village idiot - but this tiny difference allowed von Neumann and Einstein to solve lots of problems that were just too hard for other mathematicians/physicists. (It follows that an artificial intelligence just a tiny bit smarter than Einstein and von Neumann would be as much more productive than them as they are in relation to other mathematician/physicists).
(Obviously other characteristics besides intelligence are very important in these fields - e.g. work ethic. I put that complication aside here, though.)
The same pattern holds in many other fields - e.g. sports. In a sense, the difference in ability between Rafael Nadal and no 300 on the ATP ranking is very small - e.g. they are hitting the ball roughly as hard, are roughly as good at, say, shooting the ball within half a metre of the base-line when not under pressure, etc - but this small difference in ability makes for a huge difference in productivity (in the sense that lots of people want to watch Nadal - which means that his games generate a lot of utility - but few people want to watch no 300).
But there are also fields where you have an entirely different pattern. The difference in productivity between the world's best cleaner and the average cleaner is, I'd guess, tiny. Similarly, if Peter is twice as strong as Paul, he will be able to fetch as much as water as needed in half the time Paul needs - neither more, nor less. In other words, the relationship between ability and productivity in these fields is linear:
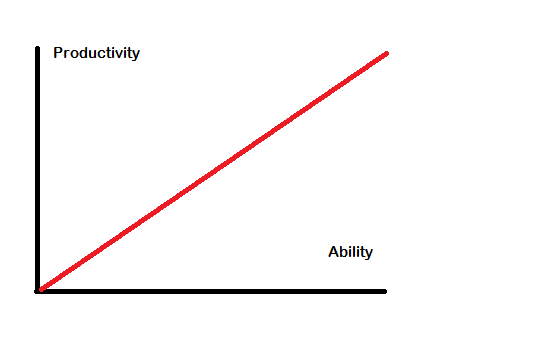
You get approximately this linear pattern in many physical jobs, but also in some intellectual jobs. Assume, for instance, that there is an intellectual field where the only thing that determines your productivity is your ability to acquire and memorize factual information. Say also that this field is neatly separated into small problems, so that your knowledge of one problem doesn't affect your ability to solve other problems. In this case, a twice as good capacity to acquire and memorize factual information will mean that you'll be able to solve twice as many of these problems - neither more nor less. Now there is obviously no intellectual field where you have exactly this pattern, but there are fields - the more "descriptive", as opposed to theoretical, social sciences come to mind - which at least approach it, and where the differences in productivity hence are much smaller than they are in theoretical physics or mathematics. (Of course, there are other patterns besides these; for instance, in some jobs, what's important is that you meet some minimum level of ability, beyond which more ability translates in very little additional productivity.)
Due to the fact that different academic disciplines have more or less the same pay structure, and are governed by similar rules and social institutions, these large differences between them are, however, seldom noted. This contributes to our inability to see how huge the differences in productivity between different scientists are in some disciplines.
The difference between these two patterns is due to the fact that the first kinds of jobs are more "social" than the latter kinds in a particular way. The usefulness of your work in theoretical physics is dependent on how good others are at theoretical physics in a way the usefulness of your water fetching isn't. Even if you're weak, you'll still contribute something by carrying a small amount of water to put out a fire, but if you're not above a certain level of cognitive ability, your work in theoretical physics will have no value whatsoever.
I suppose that economists must have written on this phenomenon - what I term other-dependent productivity. If so I'd be interested in that and in adopting their terminology.
I think one reason why people have trouble accepting Yudkowsky's picture is that they note how vastly much more productive Einstein was than an average physicist (let alone the village idiot...) and then infer that this difference must be due to a vast difference in intelligence. Hence pointing out that the difference in productivity could be vast even though the difference in intelligence is not, due to the fact that productivity in theoretical physics is strongly other-dependent, should make people more disposed to accept Yudkowsky's picture.
It would be interesting to discuss what the relationship between ability and productivity is in different jobs and intellectual fields. I leave that for later, though. Obviously, the question of how ability is to be defined is relevant here. This question was extensively discussed in the comments to Yudkowsky's post but I have avoided to discuss it for two reasons: firstly, because I think it is possible to get an intuitive grasp of the phenomena I'm discussing without a precise definition of ability, and, secondly, because an extensive discussion of this notion would have made the post far too long and complicated.
Edit: Here is a relevant article I just found on Marginal Revolution on "winner-take-all economies" where "small differences in skills can mean large differences in returns". It also has some useful tips for further reading.