I want to talk about a few different approaches to general problem solving (for humans). It turns out that they can all be applied to mazes, so I’ll use some disney-themed mazes to illustrate each approach.
We’ll start off with some traditional path-search algorithms (DFS, BFS, heuristic). Next, we’ll talk about how these algorithms can fall short for everyday problem solving. Then we’ll move on to the interesting part: two techniques which often work better for everyday problem solving, and lend some interesting insights when applied to mazes.
I’ll assume no technical background at all, so if you’ve seen some of this stuff before, feel free to skim it.
DFS and BFS
You have a maze, with a start point and an end point, and you are searching for a path through it. In algorithms classes, this problem is called “path search”.

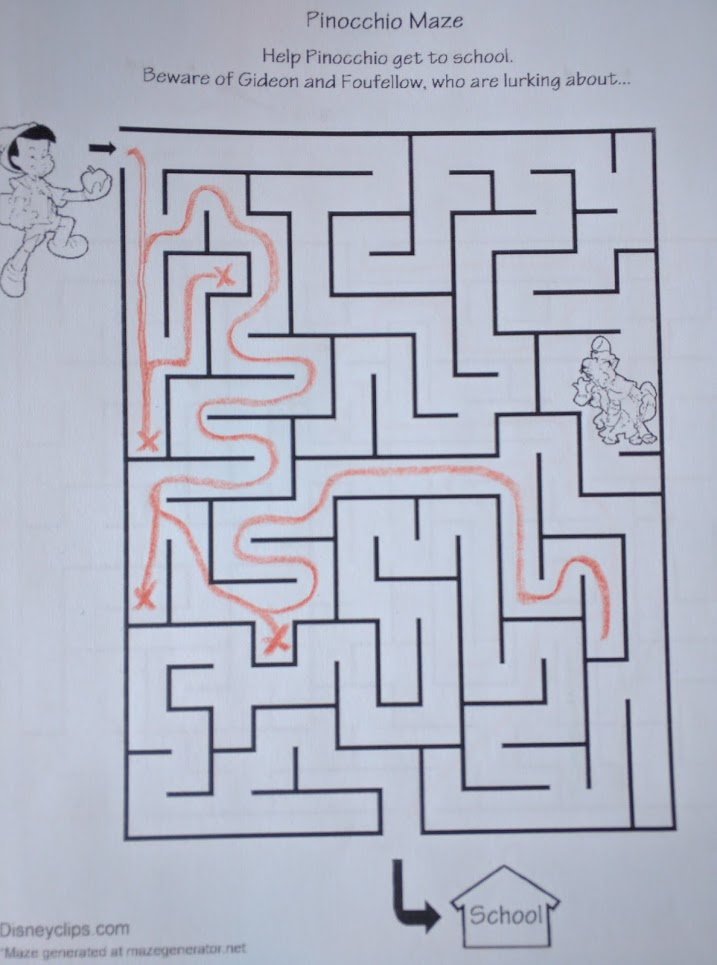
The very first path search algorithms students typically learn are depth-first search (DFS) and breadth-first search (BFS). Here’s DFS, applied to the Pinocchio maze above:
Basically, the DFS rule is “always take the right-most path which you haven’t already explored”. So, in the Pinoccchio maze, we start out by turning right and running until we hit a wall (the first “x”). Then we turn around and go back, find another right turn, and hit another dead end. Turn around again, continue…
That’s depth-first search. We go as far as we can down one path (“depth-first”) and if we hit a dead end, we turn around, back up, and try another path.
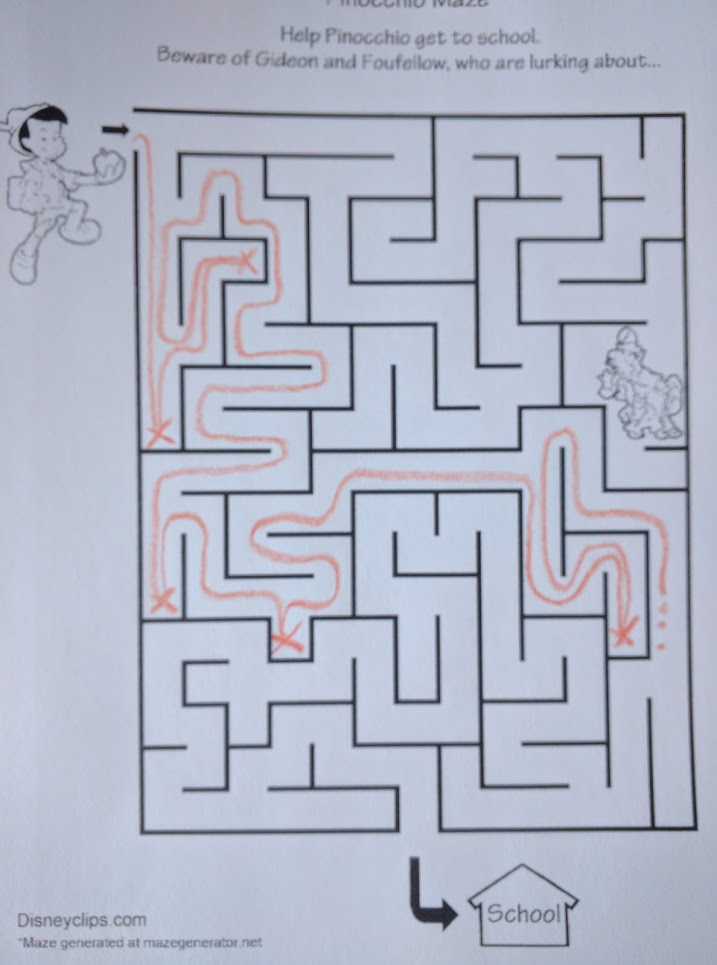
Breadth-first search, on the other hand, tries all paths in parallel:
In this snapshot, we’ve hit three dead ends, and we have four separate “branches” still exploring the maze. It’s like a plant: every time BFS hits an intersection, it splits and goes both ways. It’s “breadth-first”: it explores all paths at once, keeping the search as wide as possible.
There’s lots more to say about these two algorithms, but main point is what they have in common: these are brute-force methods. They don’t really do anything clever, they just crawl through the whole maze until they stumble on a solution. Just trying out paths at random will usually solve a maze about as quickly as DFS or BFS (as long as you keep track of what you’ve already tried).
Let’s be smarter.
Heuristic Search
A human solving a maze usually tries to work their way closer to the end. If we’re not sure which way to go, we take the direction which points more toward the goal.
Formalizing this approach leads to heuristic search algorithms. The best-known of these is A*, but we’ll use the more-human-intuitive “greedy best-first” search. Like breadth-first search, best-first explores multiple paths in parallel. But rather than brute-force searching all the paths, best-first focuses on paths which are closest to the goal “as the bird flies”. Distance from the goal serves as an heuristic to steer the search.
Here’s an example where best-first works very well:
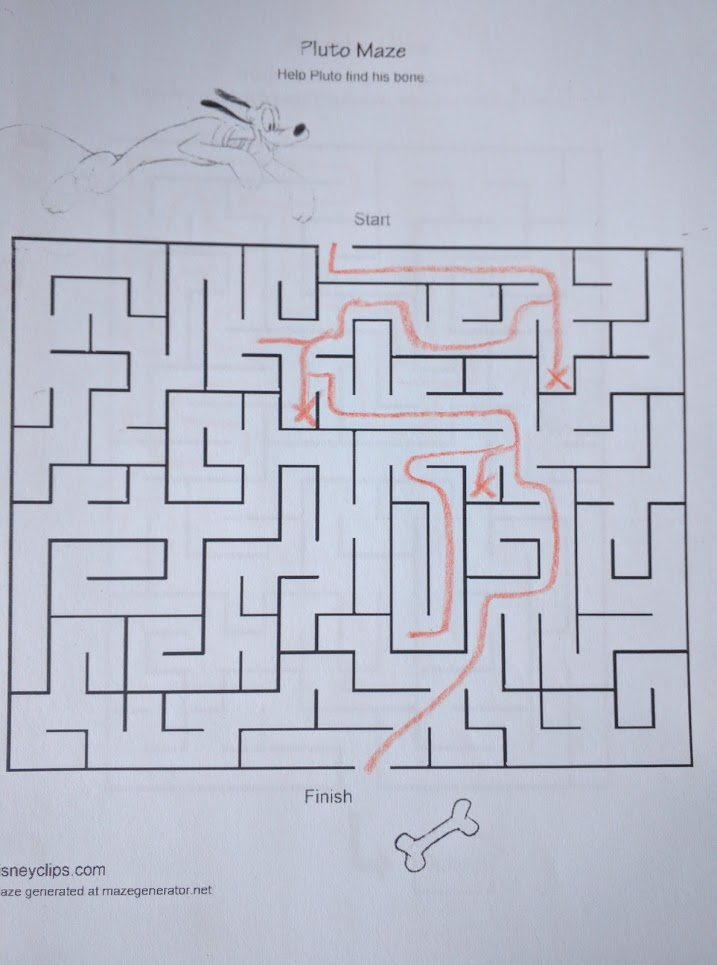
By aggressively exploring the path closest to the goal, Pluto reaches his bone without having to explore most of the maze.
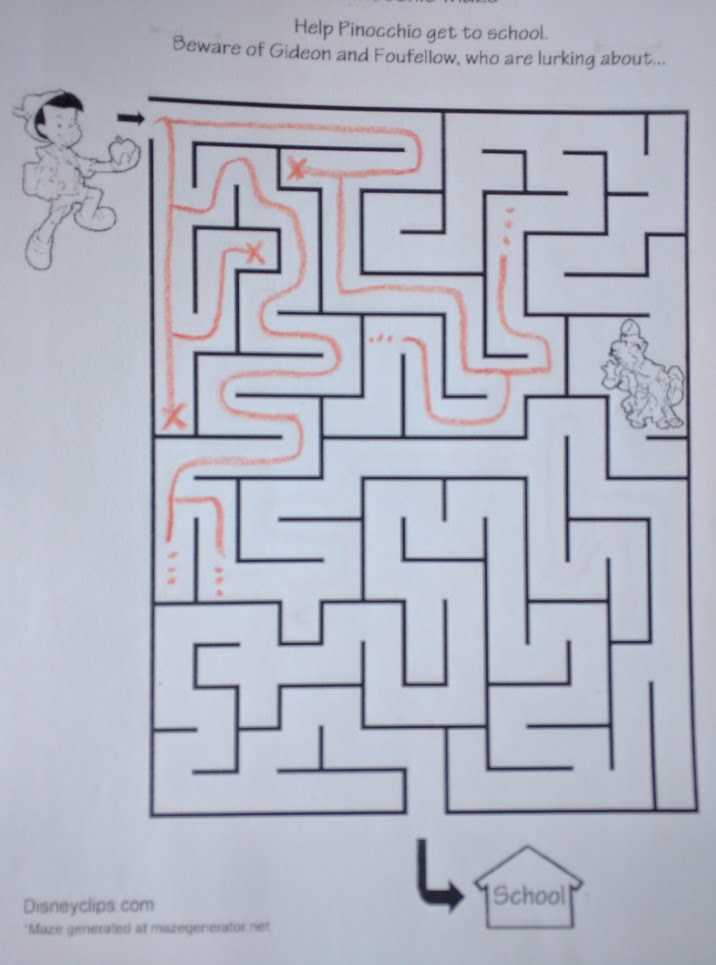
But heuristic search comes with a catch: it’s only as good as the heuristic. If we use straight-line distance from the goal as an heuristic, then heuristic search is going to work well if-and-only-if the solution path is relatively straight. If the solution path wiggles around a lot, especially on a large scale, then heuristic search won’t help much. That’s what happens if we apply best-first to the Pinocchio maze:
… the best-first solution in this case is almost identical to DFS.
General Problem Solving
In AI, path search is used to think about solving problems in general. It turns out all sorts of things can be cast as path search problems: puzzles, planning, and of course navigation. Basically any problem whose solution is a sequence of steps (or can be made a sequence of steps).
What do our maze-solving algorithms look like in a more general problem-solving context?
Brute-force search is, well, brute-force search. It’s trying every possible solution until you hit on one which works. If we use the random variant, it’s randomly trying things out until you hit something which works. I do not recommend solving problems this way unless they are very small, very simple problems.
Heuristic search is more like how most people solve problems, at least in areas we aren’t familiar with. We’ll have some heuristics, and we’ll try stuff which the heuristics suggest will work well.
One common version of heuristic search in real-world problem solving is babble and prune: brainstorm lots of random ideas, then pick out a few which seem promising based on heuristics. Lather, rinse, repeat. This goes by many names; in design, for example, it’s called “flare and focus”. It’s like e-coli path search: flail around, run in a random direction, and if it looks like it’s working, keep going. Otherwise, flail around some more and run in a new direction.
The problem with any heuristic search is that it’s only as good as our heuristic. In particular, most heuristics are “local”: like the straight-line distance heuristic, they’re bad at accounting for large-scale problem structure. Without some knowledge of large-scale problem structure, local heuristics will lead us down many dead ends. Eventually, when we find the “right” solution, we realize in hindsight that we weren’t really solving the right problem, in some intuitive sense — more on that later.
Upping our Game
So we have algorithms which correspond to blindly flailing about (brute force), and we have algorithms which roughly correspond to how humans solve many problems (heuristics). But the real goal is to come with better ways for us humans to solve problems. We need to up our game.
For single-shot problem solving, it’s tough to do better than heuristic path search. One way or another, you have to explore the problem space.
But in the real world, we more often face multiple problems in the same environment. We have jobs, and our jobs are specialized. It’s like needing to find paths between many different pairs of points, but all in the same maze. In this context, we may be able to invest some effort up-front in better understanding the problem space (e.g. the maze) in order to more easily solve problems later on.
(Technical note: here, the usual textbook pathfinding algorithms are not so good. All-pairs path search tries to explicitly represent distances between each pair of points, which is out of the question for real-world high-dimensional problem solving.)
Bottlenecks
Here’s an interesting way to look at the Pinocchio maze:
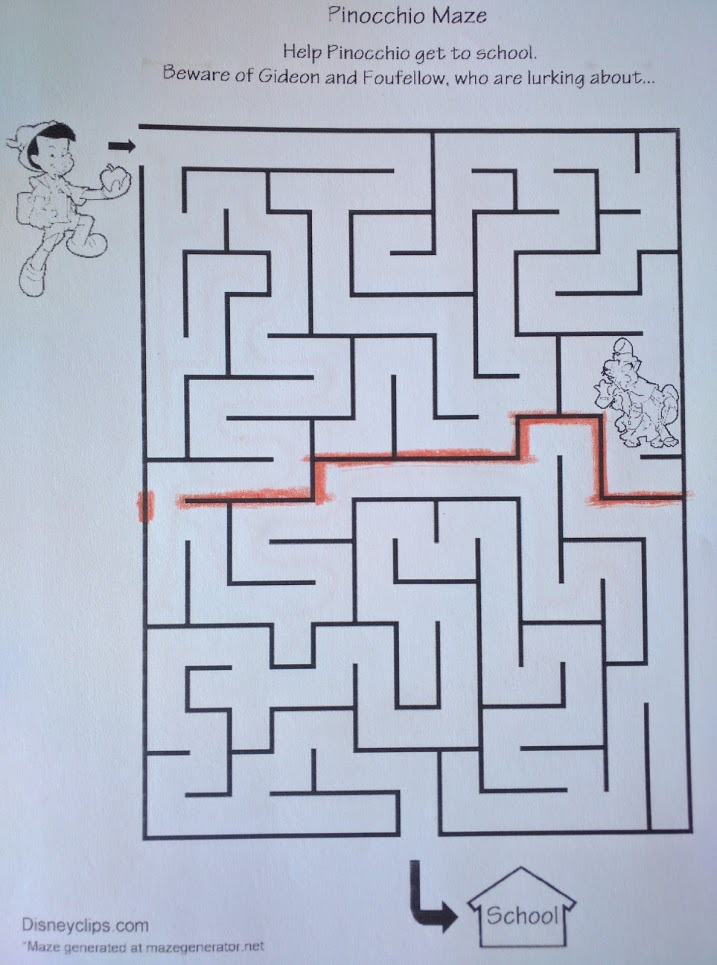
Note that the highlighted walls have exactly one gap in them. If Pinocchio wants to get from one side of the highlighted walls to the other, then he has to go through that gap.
This observation lets us break the original problem up into two parts. First, Pinocchio needs to get from the start to the gap. Next, he has to get from the gap to the end. During the first half, he can completely ignore all of the maze below the highlight; during the second half, he can completely ignore all of the maze above the highlight.
This is a bottleneck: it’s a subproblem which must be solved in order to solve the main problem.
Once we have identified a bottleneck, we can use it in conjunction with other search algorithms. For instance, rather than running heuristic search on the full maze, we can use heuristic search to get Pinocchio to the gap in the wall, and then run a second heuristic search from the gap to the end. This will do at least as well as the original heuristic search, and usually better.
Even more powerful: unlike search methods, a bottleneck can be re-used for other problems. It’s a property of the problem space, not the problem itself. If Pinocchio is starting anywhere in the top half of the maze, and needs to get anywhere in the bottom half, then the same bottleneck applies. It can even be useful to know about the bottleneck when we don’t need to solve it for the problem at hand; consider this maze:
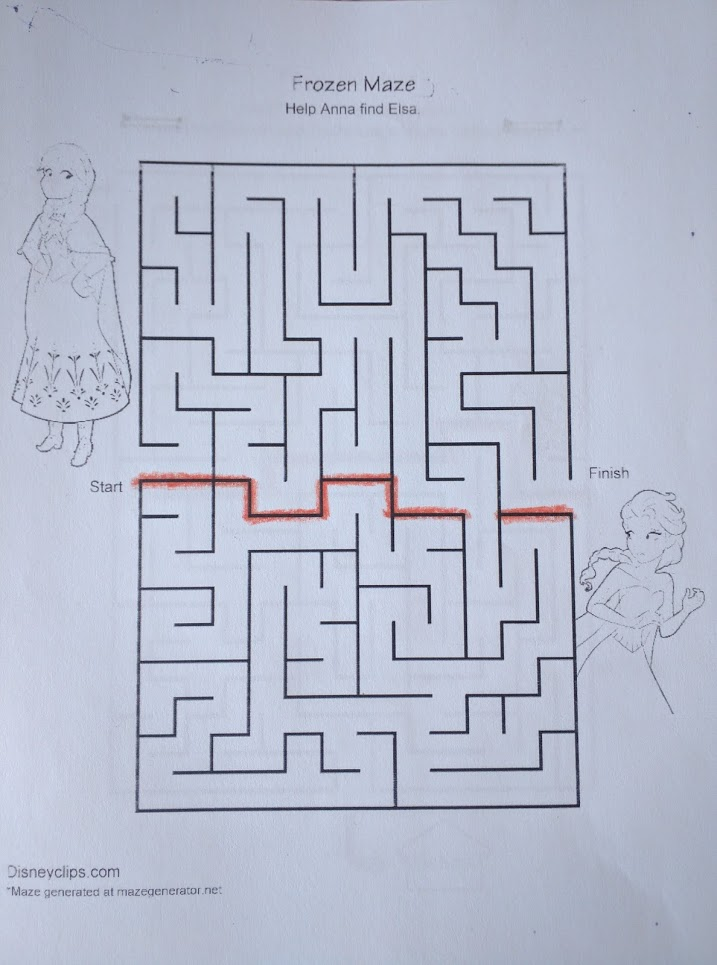
Having identified the bottleneck, we can see at a glance that the entire bottom half of the maze is irrelevant. If Anna crosses the gap, sooner or later she’ll have to turn around and come back out again in order to reach Elsa. In other words: knowing about a bottleneck you don’t need to solve is useful, because you can avoid it.
Bottlenecks in Real-World Problems
Note that, in order for the bottleneck to add value on top of heuristic search, the bottleneck should be something which the heuristic search would not efficiently solve on its own. For instance, if we’re using a straight-line-distance heuristic in a maze, then a bottleneck is most useful to know about if it’s notnear the straight line between start and finish. If there’s a bottleneck we must cross which is way out to the side, then that’s a useful bottleneck to know about.
Another way to word this: the ideal bottleneck is not just a subproblem which must be solved. It’s a maximally difficult subproblem, where difficulty is based on the original heuristics.
This is how we usually recognize bottlenecks in real-world problems. If I’m a programmer trying to speed up some code, then I time each part of the program and then focus on the section which takes longest: the slowest part is the “most difficult” subproblem, the limiting factor for performance. If I want to improve the throughput of a factory, then I look for whichever step currently has the lowest throughput. If I’m designing a tool or a product, then I start by thinking about the most difficult problem which that product needs to solve: once that’s figured out, the rest is easier.
Personally, I find a lot of “shower insights” come this way. I’m thinking about some problem, mulling over the hardest part. I focus in on the hard part, the bottleneck itself, forget about the broader context… and suddenly realize that there’s a really nice solution to the bottleneck in isolation. What’s hard with the original heuristic often becomes easy when we focus on the bottleneck itself, and apply bottleneck-specific heuristics.
In a maze, a bottleneck way to the side is hard using the straight-line distance to the finish as an heuristic. But if we aim for the gap in the wall from the start, then it’s easier.
To find the “right” solution, focus on the right problem. That’s what bottlenecks are all about.
Chunking
Let’s go back to the Anna and Elsa maze. Here’s an equivalent way to represent the bottleneck we highlighted in that maze:
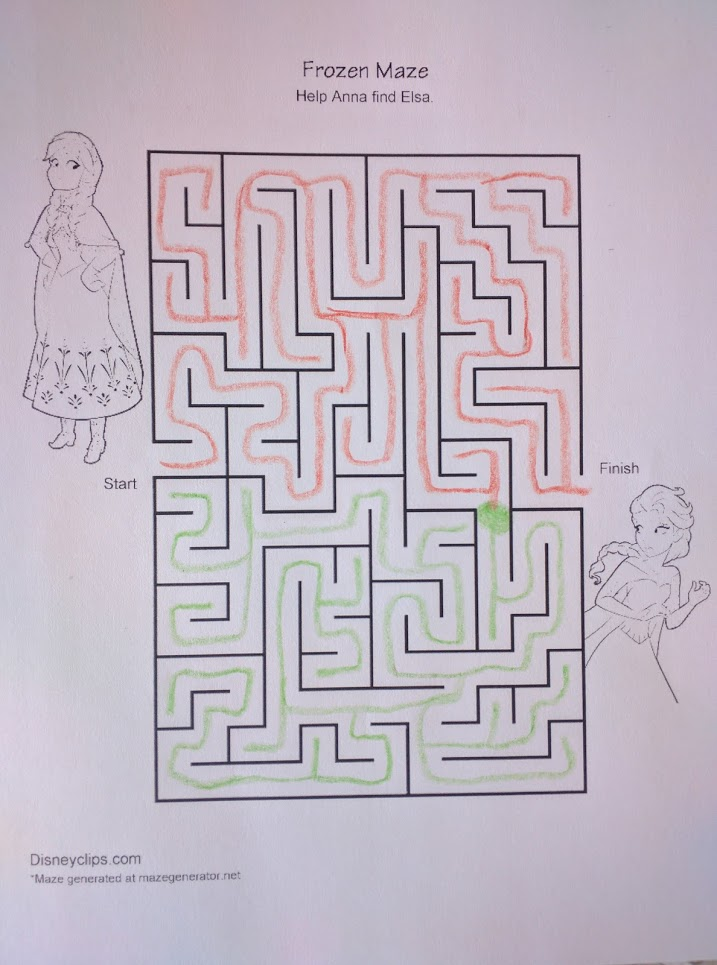
Half the maze is orange, the other half is green, and the two touch at exactly one point: the green dot, right where we identified a bottleneck. If we want to go from an orange point to another orange point, then we only need to worry about the orange part of the maze. If we want to move between orange and green, then we must cross the green point.
Here, we’ve “chunked” the maze into two pieces, and we can think about those two pieces more-or-less independently. Here’s chunking on the Pinocchio maze, with a few more colors:
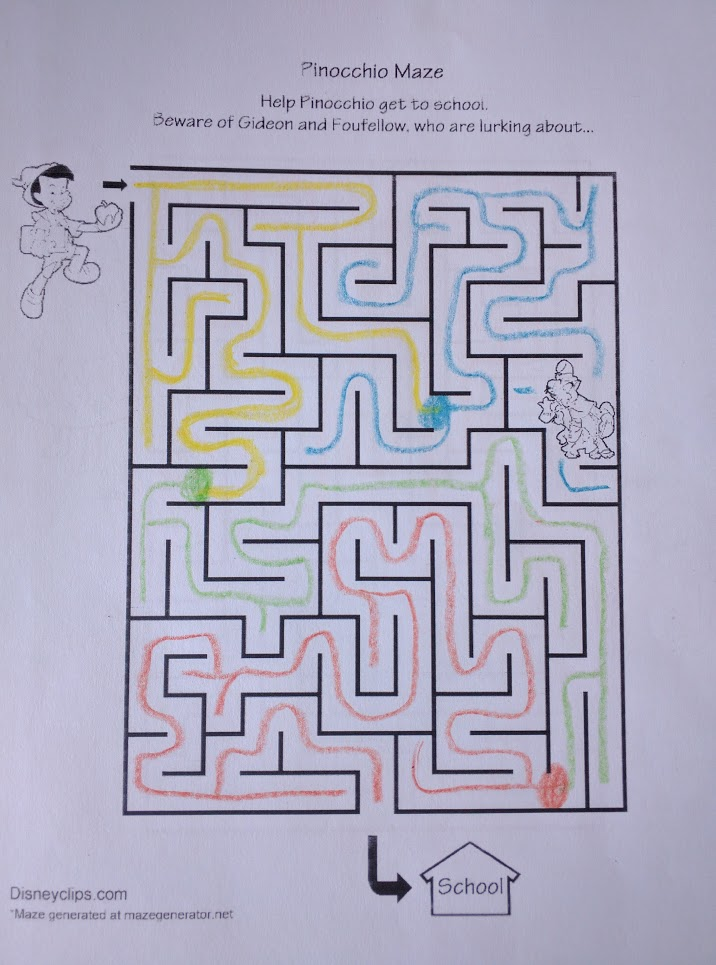
For Pinocchio to get to school, he must start in the yellow chunk and get to the orange chunk. We can only get from yellow to orange via green, so the color path must be yellow -> green -> orange (and we can ignore the blue part of the maze entirely). The original maze is broken into three parts, one within each color chunk, and each problem can be solved separately.
(Side question: there’s at least one more-human-intuitive way to apply chunking to mazes. Can you figure it out?)
Once we’ve represented the maze using colored chunks, and once we know how to use that information, we can use it to move between any two points in the maze. “Local” moves, within the same color chunk, can ignore all the other chunks. Larger-scale travel can focus first on the sequence of color moves — essentially a path through a larger-scale, more abstracted maze — and then zoom in to find paths within each chunk. Ideally, we choose the chunks so that an heuristic works well within each piece.
This is actually how humans think about moving around in space. Our mental map of the world contains five or six different levels, each one more granular than the last. When planning a path, we start with the highest-abstraction-level map, and then zoom in.
More generally, experts in a field process information more efficiently by chunking things together into more abstract pieces. Expert chess players don’t think in terms of individual pieces; they think in terms of whole patterns and how they interact. For a human, this is basically what it means to understand something.
Conclusion
I frequently see people tackle problems with tools which resemble heuristic path search — e.g., a brainstorming session, followed by picking out the most promising-sounding ideas.
I think a lot of people just don’t realize that there are other ways to tackle a problem. It’s possible to look at properties of the problem space — like bottlenecks or chunks — before proposing solutions. These are (some of) the pieces from which understanding is built, and when they work, they allow much more efficient and elegant approaches to problems.