Background: The Language-Learning Argument

How many functions are there from a 1 megabyte image to a yes/no answer to the question “does this image contain an apple?”.

Well, there are 8M bits in the image, so $2^{8000000}$ possible images. The function can assign “yes” or “no” independently to each of those $2^{8000000}$ images, so $2^{2^{8000000}}$ possible functions. Specifying one such function by brute force (i.e. not leveraging any strong prior information) would therefore require $2^{8000000}$ bits of information - one bit specifying the output on each of the $2^{8000000}$ possible images. Even if we allow for some wiggle room in ambiguous images, those ambiguous images will still be a very tiny proportion of image-space, so the number of bits required would still be exponentially huge.

Empirically, human toddlers are able to recognize apples by sight after seeing maybe one to three examples. (Source: people with kids.)

Point is: nearly-all the informational work done in a toddler’s mind of figuring out which pattern is referred to by the word “apple” must be performed by priors and general observations of the world, not by examples of apples specifically. Before the toddler ever hears the word, they must already have some internal data structure which represents the-things-we-call-apples as a natural category (though possibly implicitly rather than explicitly), just waiting to have a word attached to it. In ML terms, nearly-all the informational work of learning what “apple” means must be performed by unsupervised learning, not supervised learning. Otherwise the number of examples required would be far too large to match toddlers’ actual performance.

Furthermore, humans are empirically able to communicate; one human can say words, the other can guess what those words refer to, and then the two humans will both agree on what physical thing was referred to by the words. Admittedly this outcome is less robust than we might like (i.e. miscommunication still happens a lot), but it happens ridiculously more often than chance, to the point where exceptions are more notable than non-exceptions.

So, not only must unsupervised learning perform nearly-all the informational work of learning what words mean, but that unsupervised learning method must also somehow coordinate on (at least roughly) the same potential-word-meanings across different humans.

We can even go a step further: other kinds of minds, like dogs or neural nets, are also able to coordinate on (at least roughly) the same potential-word-meanings as humans. For now they usually require a lot more examples than human children, but nowhere near the exponentially huge number required to learn meanings by full brute force. Most of the informational work must still be done by some unsupervised process.

What We’ll Do In This Post

The language-learning argument adds up to a weak version of the Natural Abstraction Hypothesis: a wide variety of minds converge to using the same “natural abstractions”, i.e. the potential-word-meanings. Those abstractions are “natural” in the sense that they’re a fairly general property of minds (i.e. priors) plus the environment; a wide variety of minds are able to learn them in an unsupervised way just from the environment plus whatever priors are common to all these different kinds of minds. 

My other writing on natural abstraction usually starts from thinking of natural abstractions as summaries of information relevant at a distance, or of information which is highly redundant - both properties which are mostly informational features of the environment, and mostly avoid explicitly talking about minds. They’re “bottom-up” notions of natural abstraction: they start from a low-level environment model, and build up to natural high-level features. The hope would be that we can later prove such features are convergently useful for minds via e.g. selection theorems.

But we can also come from a “top-down” direction: start from the idea of natural abstractions as features used convergently by a wide variety of minds. For instance, taking a theoretical angle, we can use a standard theoretical model of minds (i.e. Bayesianism), combine it with some natural criterion which might make a feature convergently useful, and ask what “natural abstractions” are implied.

That’s the idea behind this post.

More specifically, we’ll start from the usual idea of a Bayesian mind which can learn the environment-distribution arbitrarily well via observation, but has some freedom around which latent variables to use in order to represent that distribution efficiently. Those latent variables are the features/concepts/potential-word-meanings. Then, we’ll ask if there’s some “minimal” or “most general” latent variables, some latents such that any other latents must contain at least as much information - the idea being that such “minimal” latents might be naturally convergent, and natural coordination points for agents to coordinate on potential-word-meanings.

Then, the main technical result: these “minimal” latents are the same natural abstractions we get from the “information which is highly redundant” or “information relevant at a distance” views.

Background: Latent Variables

Here’s a standard conceptual model for how an agent figures out the concept of e.g. trees. First, the agent receives a bunch of observations from the world (images, for instance), many of which show what you or I would call trees. The agent then clusters together data based on similarity. More precisely, the agent looks for patterns which are well-modeled (i.e. compressed) by assuming that they were generated in the same way. For instance, all those subimages which show what you or I would call trees can be compressed a lot by assuming that there’s a common pattern-generator (i.e. the general concept of “trees”), which is mostly not generating the patterns in other subimages. That common pattern-generator, or whatever set of variables parameterize the pattern-generator, is the “latent” variable.

Mathematically, we usually assume that the latent variable summarizes all the information which any subset of the trees tells us about the rest - i.e. by observing particular trees, we learn general facts about trees (including general facts about particular tree-species), which in turn tell us about the rest of the trees. That means the individual tree-instances are all conditionally independent, given the latent variable. That’s the most common form used for Bayesian clustering models: we try to simultaneously cluster and fit latents such that instances in the same cluster are independent given that cluster’s latent.

The standard formula: we have a bunch of instances $X_1,\dots ,X_N$ all in the same cluster. Then, conditional on the latent variable $\Lambda$, the instances should be independent:

$P[X_1,\dots ,X_N|\Lambda ]={\prod }_{i}P\left[X_i|\Lambda \right]$

Or, graphically:

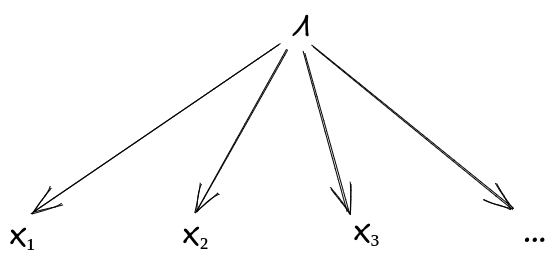
(There is some room to complain here - for instance, maybe it intuitively seems like the concept of trees should only include general facts about trees, not about specific species of tree, so instances from the same species should not be independent even conditional on the general concept of trees. We’ll come back to that near the end of the post, once we’ve connected this all back to other approaches to natural abstraction.)

Under this frame, the latents themselves take center stage, and the clusters become less central. Given the latent concept of trees, it’s pretty easy to recognize a tree; the interesting question is what models/parameterizations/etc to use for the general model of trees. More generally, given the latents, it’s relatively easy to compute the probability that any particular instance was generated by a particular latent (i.e. figure out what cluster the instance is in). The main question is what latent models/parameterizations/etc to use for each cluster.

And that’s where the notion of “minimal” or “most general” latents enters.

“Minimal” Latents

The key condition for a valid latent is that each instance be independent given the latent. All trees must be independent given the general concept of/facts about trees. But that still leaves a lot of options. For instance, we could declare that the tree-concept consists of all facts about all trees ever. Mathematically, $\Lambda =(X_1,\dots ,X_N)$. That is obviously a terrible choice; we gain nothing by using that latent. But it does technically satisfy the conditional independence requirement.

What we’d really like is a latent on the other end of the spectrum - one which includes as little information about the instances as possible, while still satisfying the conditional independence condition. Conceptually, I’ll operationalize that as follows: first, I want some latent which satisfies the conditional independence condition. Second, if anyone else comes along with another latent which satisfies the conditional factorization condition, then I should find that their latent contains at least all the information about the instances which is present in my latent. Or, to put it differently: all information in ${\Lambda }^{\ast }$ about $X_1,\dots ,X_N$ must also be present in any other $\Lambda$ which satisfies the conditional independence condition. Third, for cleanliness, we’ll assume that ${\Lambda }^{\ast }$ doesn’t contain any extra “irrelevant” information, e.g. random bits which have nothing at all to do with $X_1,\dots ,X_N$. (The third condition just eliminates some obviously-silly possibilities; we’ll mostly ignore it.)

Mathematically: call my special minimal latent ${\Lambda }^{\ast }$. First, ${\Lambda }^{\ast }$ must itself satisfy the conditional independence condition:

$P[X_1,\dots ,X_N|{\Lambda }^{\ast }]={\prod }_{i}P\left[X_i|{\Lambda }^{\ast }\right]$

Second, given any other $\Lambda$ which satisfies the conditional independence condition, $\Lambda$ must contain at least all the information in ${\Lambda }^{\ast }$ about $X_1,\dots ,X_N$. Graphically,

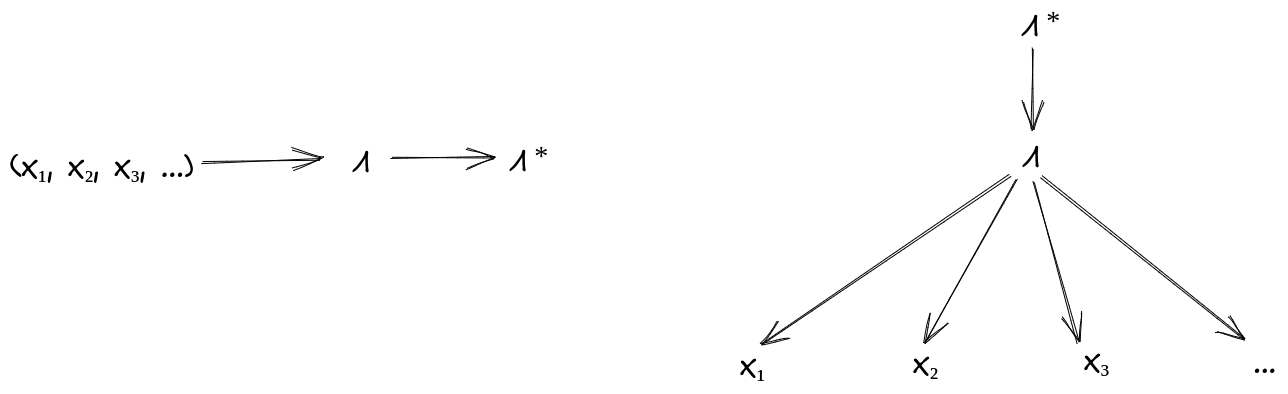
That second diagram, in equation form:

$P[{\Lambda }^{\ast },\Lambda ,X_1,\dots ,X_N]=P\left[{\Lambda }^{\ast }\right]P\left[\Lambda |{\Lambda }^{\ast }\right]{\prod }_{i}P\left[X_i|\Lambda \right]$

Caution: the notation and wording have hidden some potentially-confusing conceptual pieces here. When I say e.g. “I have a latent $\Lambda$” or “I want some latent $\Lambda$”, what I really have/want is not the value of random variable $\Lambda$, but rather the factorization of the distribution $P[X_1,\dots ,X_N]$ using $\Lambda$, i.e.

$P[X_1,\dots ,X_N]={\sum }_{\Lambda }{\prod }_{i}P\left[X_i|\Lambda \right]P\left[\Lambda \right]$

In other words, I have/want a way to model the distribution of $X$ using $\Lambda$ as a latent, and $\Lambda$ is in some sense “defined by” the distributions I use. The relevant mathematical object is not $\Lambda$ itself, but rather the distributions $P\left[\Lambda \right]$ and $\left\{P\right[X_i|\Lambda \left]\right\}$, which must reproduce the observed distribution over $X$. Similarly, the condition on $\Lambda$ and ${\Lambda }^{\ast }$ asserts that there exists some joint distribution $P[{\Lambda }^{\ast },\Lambda ,X_1,\dots ,X_N]$ such that the factorization holds, and the marginals match the given distributions $\left\{P\right[X_i|\Lambda \left]\right\}$, $\left\{P\right[X_i|{\Lambda }^{\ast }\left]\right\}$, $P\left[\Lambda \right]$, $P\left[{\Lambda }^{\ast }\right]$. Another way to say this: if I later learn that some other person is using a different latent-factorization to model the same tree-cluster as me, with the same observable distribution over the same physically-observable trees $X$, then I should be able to model their latent, and my latent and the observables all in one distribution $P[{\Lambda }^{\ast },\Lambda ,X_1,\dots ,X_N]$, while still being consistent with all the marginals and the conditions.

Anyway, the big question now is: when can I find some ${\Lambda }^{\ast }$ which satisfies all conditions - i.e. ${\Lambda }^{\ast }$ which satisfies the conditional independence condition and contains at least as little info as any other $\Lambda$ which satisfies the conditional independence condition?

The Connection to Redundancy

Now for the main trick. To illustrate, we’ll start with a simplified case, in which we have only two instances $X_1$ and $X_2$ (e.g. only two trees).

Our “minimality” condition says that all information about $(X_1,X_2)$ which is in ${\Lambda }^{\ast }$ must also be in $\Lambda$, for any other latent $\Lambda$ allowed by conditional independence. So, we’re allowed to pick any latent $\Lambda$ such that $X_1$ and $X_2$ are independent given $\Lambda$. Well, $X_1$ is always independent of everything (including $X_2$) given $X_1$ itself. Likewise, $X_2$ is always independent of everything (including $X_1$) given $X_2$ itself. So, we could pick either $X_1$ or $X_2$ to be $\Lambda$.

Our “minimal” ${\Lambda }^{\ast }$ must therefore satisfy:

• All information about $(X_1,X_2)$ which is in ${\Lambda }^{\ast }$ must also be in $X_1$
• All information about $(X_1,X_2)$ which is in ${\Lambda }^{\ast }$ must also be in $X_2$

In other words: all information about $(X_1,X_2)$ which is in ${\Lambda }^{\ast }$ must be redundantly present in both $X_1$ and $X_2$. We must have both:

• $\Lambda$ independent of $X_1$ given $X_2$, and
• $\Lambda$ independent of $X_2$ given $X_1$

Generalizing beyond the two-instance case, we can’t just use $X_i$ as a latent any more; two tree are not necessarily independent given a third tree. But we can use all but one tree as a latent - i.e. $X_{\ne i}$. Any subset of the $X_i$’s are independent given all but one $X_i$. Our “minimal” latent ${\Lambda }^{\ast }$ must therefore satisfy: all information about $(X_1,\dots ,X_N)$ which is in ${\Lambda }^{\ast }$ must also be in $X_{\ne i}$ for any $i$. Any choice of all-but-one instance must still include the information in ${\Lambda }^{\ast }$. In that sense, ${\Lambda }^{\ast }$ depends on only the “perfectly redundant” information in $(X_1,\dots ,X_N)$.

This connects us directly to natural abstractions as redundant information. Indeed, we can carry over the same idea from that formulation: since $X_{\ne i}$ contains all the information relevant to ${\Lambda }^{\ast }$, we can resample any $X_i$ individually without changing our information about ${\Lambda }^{\ast }$. Therefore, ${\Lambda }^{\ast }$ can only depend on $X$ via quantities conserved under repeatedly resampling each $X_i$ individually.

Now to answer our big question from the previous section: I can find some ${\Lambda }^{\ast }$ satisfying the conditions exactly when all of the $X_i$’s are independent given the “perfectly redundant” information. In that case, I just set ${\Lambda }^{\ast }$ to be exactly the quantities conserved under the resampling process, i.e. the perfectly redundant information itself. Conversely, if the $X_i$’s are not independent given the perfectly redundant information, then I can’t find any ${\Lambda }^{\ast }$ satisfying the conditions.

(A somewhat more complete proof is in A Correspondence Theorem, though it doesn’t make explicit the connection to resampling because the resampling framework for natural abstraction didn’t yet exist when it was written. The results here are essentially a repackaging of that correspondence theorem, but with context, hindsight and a lot more understanding of natural abstraction from other angles.)

The Connection to Information At A Distance

Via redundancy, we can also connect to natural abstraction as information relevant at a distance. By the Telephone Theorem, in order for information to propagate over a long distance, it needs to be near-perfectly conserved through many intermediate layers; therefore the information is arbitrarily-perfectly redundantly represented in the variables constituting each of those layers. Conversely, in a local model (i.e. a model where most things only interact directly with a few “nearby” things), information needs to propagate over a long distance in order to reach very many variables, and therefore needs to propagate over a long distance in order to be redundantly represented in very many variables. Thus the equivalence between information relevant at a distance and highly redundant information, at least in local models. (Abstractions as Redundant Information contains more formal and fleshed-out versions of these arguments, though still not fully rigorous.)

That said, our conditions for ${\Lambda }^{\ast }$ so far aren’t quite equivalent to information relevant at a distance. Information relevant at a distance requires massive redundancy, information redundantly represented in many different “places” (i.e. many different $X_i$ or disjoint subsets thereof). In other words, we have to be able to throw away a whole bunch of $X_i$’s and still be able to reconstruct ${\Lambda }^{\ast }$. Our conditions so far only require enough redundancy to throw away one $X_i$ at a time, and still reconstruct ${\Lambda }^{\ast }$. If exactly two trees have some perfectly redundant information between them, and that information is entirely absent from all other trees, that would be included in ${\Lambda }^{\ast }$ under our current conditions, but might be omitted from information relevant at a distance (modulo some degrees of freedom around what to consider the low-level variables and what corresponding notion of “distance” to use, e.g. if we have separate variables for the state of each tree at each time then even a single tree may be very redundant and contain info relevant to that same tree at a far-distant time). So: ${\Lambda }^{\ast }$ includes all information relevant at a distance (at least when ${\Lambda }^{\ast }$ exists at all), but may include some other stuff too.

That said, since we’ve found that ${\Lambda }^{\ast }$ doesn’t always exist, our conditions probably aren’t quite right anyway. Let’s fix that.

Weakening the Conditional Independence Requirement

We have a minor problem: if the $X_i$’s are not conditionally independent given whatever perfectly redundant information they contain, then there isn’t any “minimal” latent satisfying the conditional independence condition.

One simple response: weaken the conditional independence condition. We already mentioned earlier that e.g. it intuitively seems like the concept of trees should only include general facts about trees, not about specific species of tree, so instances from the same species should not be independent even conditional on the general concept of trees. Maybe we can still require most trees to be independent given the general latent concept of trees, but allow for some exceptions?

Coming from another direction: when formulating natural abstractions as information relevant at a distance, the key condition is not that all the variables be conditionally independent, but that variables “far apart” be conditionally independent. Since locality in a large model implies that most variables are “far apart” from most other variables, weakening the conditional independence condition to conditional independence amongst most variables again makes sense.

So, here’s a new conditional independence condition for “large” systems, i.e. systems with an infinite number of $X_i$’s: given $\Lambda$, any finite subset of the $X_i$’s must be approximately independent (i.e. mutual information below some small $ϵ$) of all but a finite number of the other $X_i$’s. Now ${\Lambda }^{\ast }$ must satisfy this new condition, and be “minimal” (in the same sense as earlier) among latents $\Lambda$ which satisfy the new condition.

Returning to our argument about redundancy and resampling: in the step where we chose $\Lambda$ to be $X_{\ne i}$, we can now instead take $\Lambda =X_{\notin S}$ for any finite subset $S$. Otherwise, the argument remains the same. As before, we take ${\Lambda }^{\ast }$ to be whatever quantities are conserved by the resampling process, i.e. the highly redundant information. But now, perfect redundancy between two variables is no longer enough for conservation in the resampling process; ${\Lambda }^{\ast }$ will only include highly redundant information, information present in enough variables that we can drop any finite subset and still exactly recompute the information. Is that highly redundant information enough to satisfy our new independence condition?

At least in systems where each variable directly interacts with only a finite number of neighbors (e.g. a Bayes net or Markov random field of bounded degree), the answer is “yes”. Similar to the arguments in the “Connection to Information At A Distance” section earlier, information would have to propagate over a long distance in order to end up relevant to infinitely many variables, and therefore by the Telephone Theorem such information must be highly redundant, so that information is fully encoded in ${\Lambda }^{\ast }$. Conditional on ${\Lambda }^{\ast }$, then, only finitely many variables can have mutual information above a given cutoff $ϵ$. The relevant mathematical argument here is that information at a distance approaches zero conditional on the quantities conserved by resampling, which is in Abstractions as Redundant Information.

I also currently expect that we can extend beyond systems in which each variable directly interacts with only a finite number of neighbors. Intuitively, it seems like ${\Lambda }^{\ast }$ should exist for large systems in full generality, under our weakened conditional independence condition. It also seems like approximate versions of the arguments should go through. But I don’t have proofs or even proof sketches for those claims yet.

Takeaways

There are currently three main framings of natural abstraction which I think about: information at a distance, highly redundant information, and minimal latents. We can view the concept of trees as:

• A summary of information about a bunch of trees which is relevant to far-away trees
• Information which is highly redundant across many trees
• The minimal latent variables which induces approximate conditional independence between most trees

(In all cases, the abstract-summarization-method is coupled with clustering to figure out which chunks of reality to consider trees in the first place.) 

For infinite systems with locality (i.e. variables only directly interact with a bounded number of neighbors), these three framings yield equivalent abstract summaries. Though I don’t have full proofs yet, I expect that the redundancy and minimal latent framings are equivalent even without locality (in which case the “information relevant far away” frame doesn’t apply, since it inherently requires locality). I'd love if someone else proved this claim, by the way!

The convergence between these three approaches to natural abstraction, which look so different at first glance, is currently one of my main pieces of mathematical evidence that they’re on the right track.