Contest: An Alien Message

Solution:

#!/usr/bin/env python3

import struct

a = [1.3, 2.1, -0.5] # initialize data
L = 2095 # total length
i = 0

while len(a)<L:
    if abs(a[i]) > 2.0 or abs(a[i+1]) > 2.0:
        a.append(a[i]/2)
        i += 1
    else:
        a.append(a[i] * a[i+1] + 1.0)
        a.append(a[i] - a[i+1])
        a.append(a[i+1] - a[i])
        i += 2

f = open("out_reproduced.bin","wb") # save in binary
f.write(struct.pack('d'*L,*a)) # use IEEE 754 double format
f.close()

Then one can check that the produced file is identical:

$ sha1sum *bin
70d32ee20ffa21e39acf04490f562552e11c6ab7  out.bin
70d32ee20ffa21e39acf04490f562552e11c6ab7  out_reproduced.bin

edit: How I found the solution: I found some of the other comments helpful, especially from gjm (although I did not read all). In particular, interpreting the data as a sequence of 64-bit floating point numbers saved me a lot of time. Also gjm's mention of the pattern a, -a, b, c, -c, d was an inspiration. If you look at the first couple of numbers, you can see that they are sometimes half of an earlier number. Playing around further with the numbers I eventually found the patterns a[i] * a[i+1] + 1.0 and a[i] - a[i+1]. It remaine... (read more)

[-]dkirmani3y146

Replicated!

[-]anonymousaisafety3y1215

I have mixed thoughts on this.

I was delighted to see someone else put forth an challenge, and impressed with the amount of people who took it up.

I'm disappointed though that the file used a trivial encoding. When I first saw the comments suggesting it was just all doubles, I was really hoping that it wouldn't turn out to be that.

I think maybe where the disconnect is occurring is that in the original That Alien Message post, the story starts with aliens deliberately sending a message to humanity to decode, as this thread did here. It is explicitly described as such:

From the first 96 bits, then, it becomes clear that this pattern is not an optimal, compressed encoding of anything. The obvious thought is that the sequence is meant to convey instructions for decoding a compressed message to follow...

But when I argued against the capability of decoding binary files in the I No Longer Believe Intelligence To Be Magical thread, that argument was on a tangent -- is it possible to decode an arbitrary binary files? I specifically ruled out trivial encodings in my reasoning. I listed the features that make a file difficult to decode. A huge issue is ambiguity because in almost all... (read more)

1blf3y

Your interlocutor in the other thread seemed to suggest that they were busy until mid-July or so. Perhaps you could take this into account when posting. I agree that IEEE754 doubles was quite an unrealistic choice, and too easy. However, the other extreme of having a binary blob with no structure at all being manifest seems like it would not make for an interesting challenge. Ideally, there should be several layers of structure to be understood, like in the example of a "picture of an apple", where understanding the file encoding is not the only thing one can do.

1anonymousaisafety3y

I have posted my file here https://www.lesswrong.com/posts/BMDfYGWcsjAKzNXGz/eavesdropping-on-aliens-a-data-decoding-challenge.

9Rafael Harth3y

Interesting, I expected the solution to be simpler, and I'm surprised you found it this quickly given that it's this complex.

5Bucky3y

This suggests a different question. For non-participants who are given the program which creates the data, what probability/timeframe to assign to success. On this one I think that I would have put a high probability to be solved but would have anticipated a longer timeframe.

3anonymousaisafety3y

https://en.wikipedia.org/wiki/Kolmogorov_complexity The fact that the program is so short indicates that the solution is simple. A complex solution would require a much longer program to specify it.

5Rafael Harth3y

Kolmogorov Complexity isn't the right measure. I'm pretty sure this program is way simpler (according to you or me) than most uniformly sampled programs of equal KC that produce a string of equal length. And i wouldn't consider it short given how hard it would be to find a "typical" program with this KC.

1anonymousaisafety3y

Why do you say that Kolmogorov complexity isn't the right measure? I am worried that you might have this backwards? Kolmogorov complexity describes the output, not the program. The output file has low Kolmogorov complexity because there exists a short computer program to describe it.

2Rafael Harth3y

Let me rephrase then: most strings of same length and same KC will have much more intuitively complex programs-of-minimum-length that generated them. Why is the program intuitively simple? Well for example, suppose you have the following code in the else block: a.append(min(max(int(i+a[i]),2),i) i += 1 I think the resulting program has lower length (so whatever string it generates has lower KC), but it would be way harder to find. And I bet that a uniformly sampled string with the same KC will have a program that looks much worse than that. The kinds or programs that look normal to you or me are a heavily skewed sample, and this program does look reasonably normal.

5Bucky3y

I don’t think this follows - your code is shorter in python but it includes 3 new built in functions which is hidden complexity. I do agree with the general point that KC isn’t a great measure of difficulty for humans - we are not exactly arbitrary encoders.

4gjm3y

Why do you think that "would be way harder to find"? (My intuition goes exactly the other way.)

5Rafael Harth3y

Eh. I agree with both replies that the example was bad. I wanted to do something unintuitive with pointer arithmetic, but the particular code probably doesn't capture it well, so it may in fact be easier to find. (Still totally stand by the broader point though.)

7gjm3y

Lovely!

2Alex Vermillion3y

Might be an obvious thought, but why did the aliens send us this gibberish. Is there an interpretation of this that makes sense?

[-]dkirmani3y100

Even more obviously, why do aliens adhere to the IEEE 754 standard? My interpretation is that the cryptanalyst from the post has indeed been pranked by their friend at NASA.

[-]gjm3y215

Interpreting each 8-byte block as an IEEE double-precision float (endianity whatever's default on x86-64, which IIRC is little-endian) yields all values in the range -4 .. 4.2. FFT of the resulting 2095 values gives (ignoring the nonzero DC term arising from the fact that the average isn't quite zero) is distinctly not-flat, indicating that although the numbers look pretty random they are definitely not -- they have more high-frequency and less low-frequency content than one would get from truly random numbers.

[-]Rafael Harth3y162

Here's what you get when you interpret them as (y,x) positions of points.

7Nnotm3y

For what it's worth, colored by how soon in the sequence they appear (blue is early, red is late) (Also note I interpreted it as 2094 points, with each number first used in the x-dimension and then in the y-dimension): Note that one line near the top appears to be drawn twice, confirming if nothing else that it's not a rule that it's not a succession rule that only depends on the previous value, since the paths diverge afterwards. Still, comparing those two sections could be interesting.

1Nnotm3y

The double line I was talking about is actually a triple line, at indices 366, 677, and 1244. The lines before come from fairly different places, and they diverge pretty quickly afterwards: However, just above it, there's another duplicate line, at indices 1038 and 1901: These start out closer together and also take a little bit longer to diverge. This might be indicative of a larger pattern that points that are close together and have similar histories tend to have their next steps close to each other as well.

6gjm3y

Every number in the sequence which equals 1-(y/2)^2 for "nice" y to "good" accuracy is in fact on the quadratic; i.e., when a number is "approximately" 1-(y/2)^2 for a y that "could" come next, that y does in fact come next. BUT to make this so I am having to define "nice" and "good" fairly tightly; this in fact occurs for only 14 values early in the sequence, perhaps before roundoff error starts being a nuisance. (I am conjecturing that the way this thing is constructed might be that we start with a few initial values and then iterate some process like: "if (condition) then next number is - previous number; else if (condition) then next number is 2sqrt(1-previous); else if ...". If so, then we might start with "nice" numbers -- in fact the first two are 1.3 and 2.1 to machine precision -- but that "niceness" might be eroded as we calculate. This is all very handwavy and there is at least one kinda-obvious objection to it.)

5gjm3y

A few reasons for suspecting that this sort of iterative process is in play: * It would fit with the relationship to "That Alien Message" where the idea is that each frame (here, each number) is the "next" state of affairs as something evolves according to simple rules. * There are many cases in which it sure looks as if one number is derived from its predecessor. (Or maybe from its successor.) * It's an obvious thing to do, if you want to set a challenge like this. Note that I am not necessarily conjecturing that each number is a function of its predecessor. There might be other internal state that we don't get to see.

1blf3y

Do you see how such an iteration can produce the long-distance correlations I mention in a message below, between floats at positions that differ by a factor of 2/e? It seems that this would require some explicit dependence on the index.

2Donald Hobson3y

Its not exactly 2/e. Here is a plot of the "error" of those points. The x axis is the larger point. The y axis is the smaller point minus 2/e times the larger. So its within about 1% of 2/e, suggesting it might be a real thing, or might just be a coincidence.

3Rafael Harth3y

Have you tried writing programs that create sequences like the above to see how close they get? (Asking to avoid redoing work if the answer is yes.)

2gjm3y

Making explicit something I said in passing elsewhere: it seems not-impossible that the sequence might be best looked at in reverse order, since mapping x to 1-(x/2)^2 or (1-x^2)/2 is somewhat more natural than going the other way. However, it does look rather as if there might be some accumulation of roundoff error in the forward direction, which if true would argue for reading it forwards rather than backwards.

5ObserverSuns3y

More structure emerges! Here's a plot of consecutive pairs of values (data[i], data[i+1]) such that data[i+1] = -data[i+2]. ![Consecutive values before a negation](https://i.imgur.com/2FRBhAz.png)

4dkirmani3y

Has anyone tried a five-dimensional representation instead of a two-dimensional one? 2095 isn't divisible by 2 or by 3, but it is divisible by 5. Maybe our "aliens" have four spatial dimensions and one temporal.

5Rafael Harth3y

I've tried highlighting every k-th point out of n with the same color for a bunch of n, but it all looks random. Right now, I've also tried using only 2 of 5 float values. It looks like a dead end, even though the idea is good. I think the data is 1-dimensional, the interesting part is how each number is transformed into the next, and the 2d representation just happens to catch that (e.g., if x is transformed into −x, it lands on the diagonal).

5Nnotm3y

Second try: When looking at scatterplots of any 3 out of 5 of those dimensions and interpreting each 5-tuple of numbers as one point, you can see the same structures that are visible in the 2d plot, the parabola and a line - though the line becomes a plane if viewed from a different angle, and the parabola disappears if viewed from a different angle.

1Nnotm3y

Looking at scatterplots of any 3 out of 5 of those dimensions, it looks pretty random, much less structure than in the 2d plot. Edit: Oh, wait, I've been using chunks of 419 numbers as the dimensions but should be interleaving them

4gjm3y

(This has y increasing downwards.) The straight line comes from the (x,-x) pairs I remarked on, which make up ~2/3 of the dataset. The parabolic thing comes from values ...,a,b,... where a = 1-(b/2)^2 to something like full precision.

2moridinamael3y

Ah, it's the Elden Ring

2Rafael Harth3y

There are 1047 points. The points on the diagonal are distributed all across the list -- here are the first indices [3,6,9,10,13,16,18,21,25,27,28,31,34,38,41,43,46,49,52,55]... They're usually 3 apart, but sometimes 1, 2, 4, 5, or 6. The last one has index 1045.

[-]gjm3y158

By the way, it's definitely not aliens. Aliens would not be sending messages encoded using IEEE754 double-precision floats.

2blf3y

Here is a rather clear sign that it is IEEE754 64 bit floats indeed. (Up to correctly setting the endianness of 8-byte chunks,) if we remove the first n bits from each chunk and count how many distinct values that takes, we find a clear phase transition at n=12, which corresponds to removing the sign bit and the 11 exponent bits. These first 12 bits take 22 different values, which (in binary) clearly cluster around 1024 and 3072, suggesting that the first bit is special. So without knowing about IEEE754 we could have in principle figured out the splitting into 1+11+52 bits. The few quadratic patterns we found have enough examples with each exponent to help understand the transitions between exponents and completely fix the format (including the implicit 1 in the significand?).

2dkirmani3y

Alternative hypothesis: The first several bits (of each 64-bit chunk) are less chaotic than the middle bits due to repetitive border behavior of a 1-D cellular automaton. This hypothesis also accounts for the observation that the final seven bits of each chunk are always either 1000000 or 0111111. If you were instead removing the last n bits from each chunk, you'd find another clear phase transition at n=7, as the last seven bits only have two observed configurations.

1blf3y

If you calculate the entropy p0log2(p0)+p1log(p1) of each of the 64 bit positions (where p0 and p1 are the proportion of bits 0 and 1 among 2095 at that position), then you'll see that the entropy depends much more smoothly on position if we convert from little endian to big endian, namely if we sort the bits as 57,58,...,64, then 49,50,...,56, then 41,42,...,48 and so on until 1,...,8. That doesn't sound like a very natural boundary behaviour of an automaton, unless it is then encoded as little endian for some reason.

2dkirmani3y

Now that I know that, I've updated towards the "float64" area of hypothesis space. But in defense of the "cellular automaton" hypotheses, just look at the bitmap! Ordered initial conditions evolving into (spatially-clumped) chaos, with at least one lateral border exhibiting repetitive behavior:

[-]gjm3y101

The first few numbers are mostly "nice". 1.3, 2.1, -0.5, 0.65, 1.05, 0.675, -1.15, 1.15, 1.70875, 0.375, -0.375, -0.3225, -2.3, 2.3. Next after that is 1.64078125, which is not so nice but still pretty nice.

These are 13/10, 21/10, -1/2, 13/20, 21/20, 27/40, -23/20, 23/20, 1367/800, 3/8, -3/8, -129/400, -23/10, 23/10, 10501/6400, ...

A few obvious remarks about these: denominators are all powers of 2 times powers of 5; 13 and 21 are Fibonacci numbers; shortly after 13/10 and 21/10 we have 13/20 and 21/20; we have three cases of x followed by -x.

5gjm3y

Slightly less than 1/3 of all numbers are followed by their negatives. Usually it goes a, -a, b, c, -c, d, etc., but (1) the first x,-x pair isn't until the 7th/8th numbers, and (2) sometimes there is a longer gap and (3) there are a few places where there's a shorter gap and we go x, -x, y, -y.

3Measure3y

Most of the breaks in the (a, -a, b, c, -c, d) pattern look like either the +/- pair was skipped entirely or the unpaired value was skipped. My guess is the complete message consists of alternating "packets" of either a single value or a +/- pair, and each packet has some chance to be omitted (or they are deterministically omitted according to some pattern).

4gjm3y

The number 23/20 appears three times. Each time it appears it is followed by a different number, and that different number is generally "unusually nasty compared with others so far". First time, at (0-based) index 7: followed by 1367/800, first with a denominator > 40. Second time, at (0-based) index 21: followed by 3.1883919921875 ~= 1632.4567/2^9, first with a denominator > 6400. Third time, at (0-based) index 48: followed by 2.4439140274654036, dunno what this "really" is, first with no obvious powers-of-2-and-5 denominator. [EDITED to fix an error.]

2Measure3y

2.4439140274654036 might be (3³x19×3671×10631)/(2¹⁹x5⁶) with some incorrect rounding (2.4439140274658203125).

2Measure3y

Value[71] is exactly half of value[49]. (and this again follows a 23)

2gjm3y

The ".4567" seems just slightly suspicious. That third number is quite close to 5005/2^11. If we multiply it by 2^11/1001, the number we actually get is 5.00013579245669; that decimal tail also seems just slightly suspicious. 1, 3, 5, 7, 9, 2, 4, 6, approximately-8. This could all be mere pareidolia, obviously.

2gjm3y

Early in the sequence (i.e., before roundoff error has much effect, if there's something iterative going on) it seems like a surprising number of our numbers have denominators that are (power of 2) x 10000. As if there's something happening to 4 decimal places, alongside something happening that involves exact powers of 2. (Cf. Measure's conjecture that something is keeping track of numerators and denominators separately.) This is all super-handwavy and I don't have a really concrete hypothesis to offer. [EDITED to add:] The apparent accumulating roundoff is itself evidence against this, because it means that after a while our numbers are not powers of 2 over 10000. So I'll be quite surprised if this turns out to be anything other than delusion. I'm leaving it here just in case it gives anyone useful ideas.

2gjm3y

These aren't all quite correctly rounded. E.g., the 12th number is about -0.3225 but it isn't the nearest IEEE754 doublefloat to -0.3225. I suspect these are "honest" rounding errors (i.e., the values were produced by some sort of computation with roundoff error) rather than there being extra hidden information lurking in the low bits.

4Donald Hobson3y

x followed by -x is common. cases where 1−xn=(xn+1/2)2 are also common.

4Measure3y

Hypothesis: the generator separately tracks the numerator and denominator and uses the xₙ₊₁ = 2*sqrt(1 - xₙ) rule exactly when this will result in both the numerator and denominator remaining integers.

5Donald Hobson3y

Here is a plot of denominator ( of the closest fraction with denominator < 1000,000,000) This looks exactly what you would expect if you started with a number that happened to be a fraction, and applied a process like squaring or adding that made the denominator bigger and bigger. This also indicates the sequence was computed from start to end, not the other way around.

4Donald Hobson3y

Well xn+1=−2√1−xn appears around as often. If this were true, there must be something aiming towards simplicity. (A huge numerator + denominator are unlikely to be squares)

3Measure3y

The second relation never occurs when xₙ is the negation of the previous xₙ₋₁. Furthermore, the second relation is always followed by xₙ₊₁ = -xₙ (i.e. there is never a "skipped pair" pattern break immediately following). This means that the skips are unlikely to be random.

1blf3y

Whenever 1−xn=(xn+1/2)2, this quantity is at most 4. I'm finding also around 50 instances of 1−2xn=(xn+1)2∈[1,4] (namely 1≤|xn+1|≤2), with again xn+2=−xn+1.

2gjm3y

It doesn't look as if there are a lot of other such relationships to be found. There are a few probably-coincidental simple linear relationships between consecutive numbers very near the start. There are lots of y=−x, quite a lot of 4x=4−y2, one maybe-coincidental 14−x=2−y2, one maybe-coincidental x=−4(1−y)2, some 2x=1−y2, and I'm not seeing anything else among the first 400 pairs. [EDITED to add:] But I have only looked at relationships where all the key numbers are powers of 2; maybe I should be considering things with 5s in as well. (Or maybe it's 2s and 10s rather than 2s and 5s.)

2gjm3y

There is one place where −xn=4(1−xn+1)2. I wonder whether there are many other relationships of broadly similar shape.

2gjm3y

The distribution of the numbers is distinctly not-uniform. Might be normal. Mean is about 0.157, standard deviation about 1.615. (I doubt these are really pi/20 and the golden ratio, but those would be consistent with the data :-).) Again, clearly not independent given how the FFT looks.

2gjm3y

Pretty sure it's not normal. The middle isn't bulgy enough. It's hard to be very confident with relatively few numbers, but I eyeballed the histogram against several batches of normals with the same mean and variance, and it's well outside what looks to me like the space of plausible histograms. I haven't bothered attempting any actual proper statistical tests. (Also, of course, if the numbers are generated by the sort of iterative process I imagine, it seems like it would be quite difficult to arrange for them to be much like normally distributed.)

[-]Donald Hobson3y70

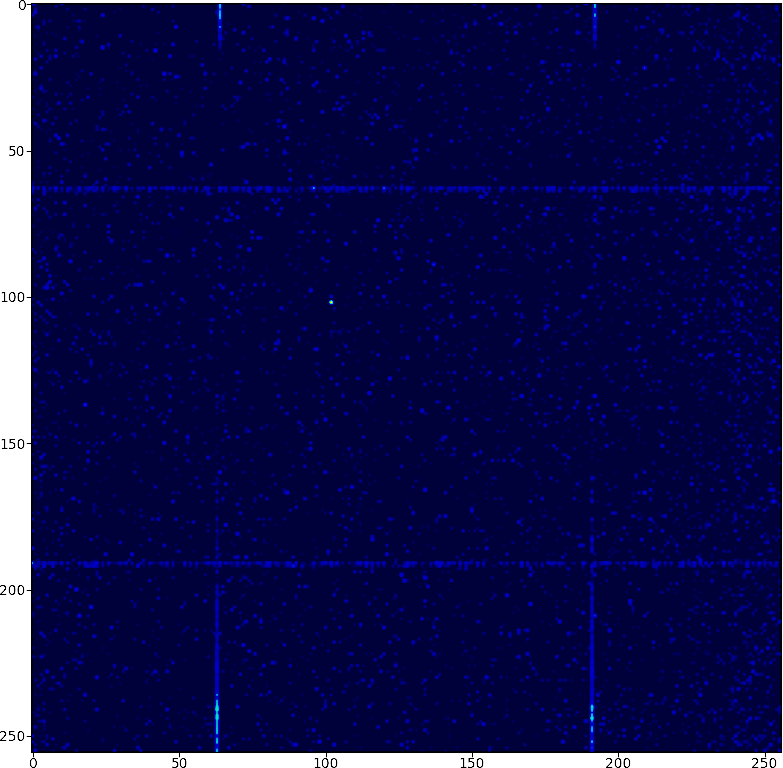
If you plot the correlation of consecutive pairs of bytes, it looks like this. The bright dot is 102, which repeats itself a fair bit at the start. The horizontal and vertical lines are 63,64,191,192 as every 8th number is one of those four values. Most of the space is 0. when a pattern appears once, it usually appears more than once. 2,4,6,8,10,12 all appear frequently.

[-]Raemon3y61

Just wanted to say I think this is a cool experiment and look forward to seeing how it plays out.

(This is somewhat betting on the contest turns out to be a well crafted experience/goal, so I guess also specifically looking to see the debrief on that)

[-]Yitz3y60

Without looking at the data, I’m giving a (very rough) ~5% probability that this is a version of the Arecibo Message.

7dkirmani3y

I turned the message into an Arecibo-style image. There are patterns there, but I can't ascribe meaning to them yet. Good luck!

5dkirmani3y

Update: I took the row-wise xor, and eliminated the redundancy on the right margin: The full image is available here.

2Alex Vermillion3y

Can you explain more how you got this? I'm trying to figure out why the left hand side of the full picture has a binary 01010101 going almost the whole way (after the header) Nevermind, I got it! Break the bits into groups of 64

2dkirmani3y

Yeah, I originally uploaded this version by accident, which is the same as the above image, but the lines that go [0,0,0, .... ,0,1,0] are so common that I removed them and represented them as a single bit on the left.

2Alex Vermillion3y

The bar on the right hand side, if you take it as high and low, has an interesting property. Pairing each high-low, it goes 1 1 10 2 8 1 3 2 4 2 15 1 8 1 3 2 15 2 ... 12 1 5 1 8 3 9 3 26 2 1 2 4 2 3 1 3 2 9 The second group (0s) is almost always pretty short, while the first group isn't as bounded.

[-]Ericf3y63

Enumerating our unfair advantages:

We know the file was generated by code
We know that code was written by a human 2a. That human was trying to simulate an extraterrestrial signal
We know that this is a puzzle, though not a "fair" puzzle like those found in escape rooms or that MIT contest. 3a. An exhaustive brainstorming of different domains of solution is warranted.

[-]Rafael Harth3y60

Well, looking at the binary data reveals some patterns; the first 6 bytes of each block of 8 start out highly repetitive, though this trend lessens later in the file. This is what it looks like as an image.

8dkirmani3y

Edit: The y-axis is inverted. The graph shows differences when it should show similarities. * Each bit of the message is 55% likely to be the the same as its predecessor; the bits of the message are autocorrelated. * If we split the message into 64-bit chunks, each bit in a given chunk has a 68% chance of being the same as the corresponding bit in the previous chunk.

4dkirmani3y

If you split the message into 64-bit chunks, the last 6 bits of each chunk are always identical. That is, they're either "000000" or "111111". I don't think there's a third spatial dimension to the data, as chunking by n*64 doesn't yield any substantial change in autocorrelation for n > 1.

2dkirmani3y

Oh, and the 7th-last bit (index [57]) is always the opposite of the final six bits. I interpret this as either being due to some cellular automaton rule, or that the "aliens" have given us six redundant bits in order to help us figure out the 64-bit reading frame.

1dkirmani3y

There's something up with the eighth bit (index [7]) of every 64-bit chunk. It has a remarkably low turnover rate (23%) when compared to its next-door neighbors. Bits [48:51] also have low turnover rates (22%-25%), but the eighth bit's low turnover rate uniquely persists when extended to context windows with lengths up to 20 chunks.

2dkirmani3y

The last seven bits of every 64-bit chunk actually carry only one bit of information. The bit right before these seven (index [56]) has an abnormally high turnover rate w.r.t. next-door neighbors(66%). Part of me wants to attribute this to some cellular automaton rule. But isn't it interesting that, in a chunk, the eighth bit is unusually stable, while the eighth-last bit is unusually volatile? Some weird kind of symmetry at play here.

4dkirmani3y

Looking at the image, two conspicuous vertical bars emerge.

[-]green_leaf3y60

See Mundane, therefore harmless.

[-]Lone Pine3y50

Thanks for doing this. I was considering offering my own version of this challenge, but it would have just been the last 50% of a file in a standard media format. That may stump one unmotivated person but probably would be easy for a large community to crack. (But what an update it would be if LWers failed that!) Anyway, I didn't have the time to do the challenge justice, which is why I didn't bother. So again, thanks!

[-]Mitchell_Porter3y52

Adding a .txt extension and translating to English produced some fun messages. :-)

2dkirmani3y

I failed to replicate this finding.

4Mitchell_Porter3y

Rename to out.bin.txt, view in Chrome, translate from Chinese to English, and you too may "recognize the spicy 5, recognize evil".

6Rafael Harth3y

Swallowing Hot.?Swallowing Hot.@ 嗫Swallowing Hot.?Swallowing Hot.?Locker Cabinet??ffffff詩ffffff.?wup= W ? ? = I wish the key ffffff 纅ffffff @q= I wish @ ?wu p= W ? p= W繩徛 (\銺? { 铽qi { 铽進?ffffff驩ffffff ?V0┯ @dffffτ?dffffτ緿韜zhen 43333 43333 @(~尮k罱? { 罱巷 { 罱巷?xu= Zhukey ffffff and fffff @V0┯侚?| 0 ?徛 (\ ? (\劭ffffff ffffff ? 1 " @0L ?0L 遵頠镢?dffff?dffffshrinking 龾澑采?潽 q琙 ?掽 q琙锟囪tBf.@山管@ ?山閇@陈 / -2兯啩Wsheng @醯sheng . Swimming cool? (For convenience :-))

[-]Donald Hobson3y40

If you let w be the first of the negation pairs, and q come before it. So the sequence goes ..., q, w, -w, ...

Then a plot of q (x axis) and w(y axis) looks like.

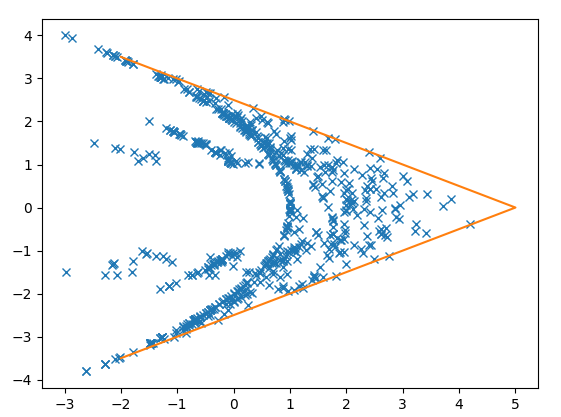
All points are within the orange line (which represents absolute(w)<-0.5*q+2.5 )

Note also that this graph appears approximately symmetric about the x axis. You can't tell between ...q,w,-w... and ...q, -w, w, ... The extra information about which item of the pair is positive resides elsewhere.

For comparison, the exact same graph, but using an unfiltered list of all points, looks like... (read more)

[-]Donald Hobson3y40

Here is the image you get if you interpret the data as floats, consider the ratio of all possible pairs, and color those with a simple ratio blue.

The pattern of horrizontal and vertical lines in the top left corner is straightforward, those numbers are individually simple fractions, so their ratio is too. The main diagonal is just numbers having a simple 1:1 ratio with themselves. The shallower diagonal lines tell us something interesting.

The non_diagonal line that is closest to diagonal means some process must be refering back to values around 73% a... (read more)

3Donald Hobson3y

What are the values along that line. Shows you multiply by 1/2, -1/2, 2 or -2.

1blf3y

These simple ratios are "always" ±2n, see my comment https://www.lesswrong.com/posts/dFFdAdwnoKmHGGksW/contest-an-alien-message?commentId=Nz2XKbjbzGysDdS4Z for a proposal that 0.73 is close to 2/e (which I am not completely convinced by).

[-]abstractapplic3y40

Misc. notes:

As we've all discovered, the data is most productively viewed as a sequence of 2095 8-byte blocks.
The eightth byte in each block takes the values 64, 63, 192, and 191. 64 and 192 are much less common than 63 and 191.
The seventh byte takes a value between 0 and 16 for 64/192 rows, weighted to be more common at the 0 end of the scale. For 63/191 rows, it takes a value between ??? and 256, strongly weighted to be more common at the 256 end of the scale (the lowest is 97 but there's nothing special about that number so the generator probably

... (read more)

[-]anonymousaisafety3y30

Some thoughts for people looking at this:

It's common for binary schemas to distinguish between headers and data. There could be a single header at the start of the file, or there could be multiple headers throughout the file with data following each header.
There's often checksums on the header, and sometimes on the data too. It's common for the checksums to follow the respective thing being checksummed, i.e. the last bytes of the header are a checksum, or the last bytes after the data are a checksum. 16-bit and 32-bit CRCs are common.
If the data represents

... (read more)

[-]blf3y30

I'm treating the message as a list of 2095 chunks of 64 bits. Let d(i,j) be the Hamming distance between the i-th and j-th chunk. The pairs (i,j) that have low Hamming distance (namely differ by few bits) cluster around straight lines with ratios j/i very close to integer powers of 2/e (I see features at least from (2/e)^-8 to (2/e)^8).

1blf3y

This observation is clearer when treating the 64-bit chunks simply as double-precision IEEE754 floating points. Then the set of pairs (i,j) for which xi/xj is ±2n for some n clearly draws lines with slopes close to powers of 2/e. But they don't seem quite straight, so the slope is not so clear. In any case there is some pretty big long-distance correlation between xi and xj with rather different indices. (Note that if we explain the first line j≃(2/e)i then the other powers are clearly consequences.)

[-]jaspax3y31

Hex dump of the first chunk of the file:

00000000: cdcc cccc cccc f43f cdcc cccc cccc 0040  .......?.......@
00000010: 0000 0000 0000 e0bf cdcc cccc cccc e43f  ...............?
00000020: cdcc cccc cccc f03f 9a99 9999 9999 e53f  .......?.......?
00000030: 6666 6666 6666 f2bf 6666 6666 6666 f23f  ffffff..ffffff.?
00000040: d8a3 703d 0a57 fb3f 0000 0000 0000 d83f  ..p=.W.?.......?
00000050: 0000 0000 0000 d8bf a070 3d0a d7a3 d4bf  .........p=.....
00000060: 6666 6666 6666 02c0 6666 6666 6666 0240  ffffff..ffffff.@
00000070: 713d 0ad7 a340 fa3f d8a3 703d 0a57

... (read more)

5gjm3y

I believe all this bit-level structure is a consequence of the values being IEEE754 double-precision values, many of them for fairly "simple" numbers, often with simple arithmetical relationships between consecutive numbers.

7jaspax3y

The nature of binary representations of floating-point is that nice bit-patterns make for round numbers and vice-versa, so I'm not sure that we can conclude a lot from that. The fact that the floating-point interpretation of the data results in numbers that cluster around certain values is telling, but could still be a red-herring. Part of my reluctance to endorse that theory is narrative: we were told that this is a simulated alien message, and what are the odds that aliens have independently invented double-precision floating point? In any case, I'm reading those threads attentively, but in the meantime I'm going to pursue some hunches of my own.

2jaspax3y

Actually, the opener is quite a bit more structured than that, even: it's three 4-byte sequences where the bytes are all identical or differ in only one bit, followed by a different 4-byte sequence. There is probably something really obvious going on here, but I need to stare at it a bit before it jumps out at me. ETA: Switching to binary since there's no reason to assume that the hexadecimal representation is particularly useful here.

6jaspax3y

Okay, here's something interesting. Showing binary representation, in blocks of 8 bytes: 00000000: 11001101 11001100 11001100 11001100 11001100 11001100 11110100 00111111 .......? 00000008: 11001101 11001100 11001100 11001100 11001100 11001100 00000000 01000000 .......@ 00000010: 00000000 00000000 00000000 00000000 00000000 00000000 11100000 10111111 ........ 00000018: 11001101 11001100 11001100 11001100 11001100 11001100 11100100 00111111 .......? 00000020: 11001101 11001100 11001100 11001100 11001100 11001100 11110000 00111111 .......? 00000028: 10011010 10011001 10011001 10011001 10011001 10011001 11100101 00111111 .......? 00000030: 01100110 01100110 01100110 01100110 01100110 01100110 11110010 10111111 ffffff.. 00000038: 01100110 01100110 01100110 01100110 01100110 01100110 11110010 00111111 ffffff.? 00000040: 11011000 10100011 01110000 00111101 00001010 01010111 11111011 00111111 ..p=.W.? 00000048: 00000000 00000000 00000000 00000000 00000000 00000000 11011000 00111111 .......? 00000050: 00000000 00000000 00000000 00000000 00000000 00000000 11011000 10111111 ........ 00000058: 10100000 01110000 00111101 00001010 11010111 10100011 11010100 10111111 .p=..... 00000060: 01100110 01100110 01100110 01100110 01100110 01100110 00000010 11000000 ffffff.. 00000068: 01100110 01100110 01100110 01100110 01100110 01100110 00000010 01000000 ffffff.@ The obvious pattern now is that every 8 bytes there is a repeated sequence of 6 bits which are all the same. Despite my initial protestations that the latter part of the file is less regular, this pattern holds throughout the entire file. The majority of the time the pattern is 111111, but there are a decent number of ones which are 000000 as well.

[-]Ericf3y30

Solution domain brainstorms (reply ti this thread with your own:

A deliberate message in an alien language
Sensor data from a pulsar, comet, or other astronomical event
An encoded image in an alien encoding scheme
A mathematical "test pattern" - possibly to serve as a key for future messages

5dkirmani3y

The output of a 1-dimensional cellular automaton, with a context window of more than one row. Or non-deterministic behavior.

[-]dkirmani3y30

The zipped version of the message is 59.47% the size of the orginal. DEFLATE (the zipping algorithm) works by using shorter encodings for commonly-used bytes, and by eliminating duplicated strings. Possible next steps include investigating the frequencies of various bytes (histograms, Huffman trees).

1dkirmani3y

Bytewise tallies: array([156, 117, 71, 90, 114, 95, 65, 59, 97, 49, 80, 60, 58, 52, 37, 57, 80, 28, 79, 53, 58, 53, 76, 31, 77, 30, 47, 41, 50, 33, 30, 28, 43, 31, 43, 36, 59, 38, 33, 37, 52, 41, 50, 37, 33, 55, 75, 52, 59, 50, 37, 44, 34, 23, 27, 51, 41, 15, 21, 46, 55, 47, 24, 903, 335, 59, 76, 38, 47, 37, 102, 47, 81, 50, 68, 33, 45, 28, 65, 38, 76, 55, 30, 42, 61, 43, 70, 74, 54, 39, 52, 48, 37, 37, 19, 49, 97, 65, 31, 55, 70, 48, 131, 60, 62, 42, 60, 64, 42, 42, 39, 39, 71, 37, 55, 49, 77, 38, 66, 23, 66, 45, 52, 37, 47, 35, 80, 43, 78, 46, 45, 36, 21, 46, 80, 38, 43, 46, 84, 47, 49, 39, 46, 54, 51, 19, 43, 32, 66, 28, 48, 56, 59, 40, 62, 41, 48, 37, 47, 20, 57, 29, 61, 26, 45, 34, 76, 74, 21, 67, 66, 30, 38, 43, 49, 56, 82, 41, 42, 54, 63, 43, 53, 74, 35, 49, 53, 47, 71, 56, 46, 798, 335, 45, 52, 65, 50, 53, 32, 52, 55, 28, 66, 35, 60, 65, 73, 48, 58, 85, 37, 58, 65, 72, 64, 58, 51, 42, 62, 59, 60, 35, 82, 55, 60, 80, 68, 77, 101, 57, 95, 73, 62, 45, 73, 45, 109, 36, 88, 84, 133, 157, 85, 117, 142, 123, 100, 95, 112, 80, 96, 82, 135, 107, 82, 84])

[-]abstractapplic3y20

If (like me) you're having a hard time reading the .bin format, here's a plaintext version of it in hexadecimal.

[-]Nnotm3y10

Interpreting the data as unsigned 8-bit integers and plotting it as an image with width 8 results in this (only the first few rows shown):

The rest of the image looks pretty similar. There is a almost continuous high-intensity column (yellow, the second-to-last column), and the values in the first 6 columns repeat exactly in the next row pretty often, but not always.

[+][comment deleted]3y10

LESSWRONG
LW

LESSWRONG
LW

95

Contest: An Alien Message

95

95

Scenario

Rules

Why is this interesting?