"- try pondering this one. Why does 2 + 2 come out the same way each time? Never mind the question of why the laws of physics are stable - why is logic stable? Of course I can't imagine it being any other way, but that's not an explanation."
Nothing in the process described, of pinpointing the natural numbers, makes any reference to time. That is why it is temporally stable: not because it has an ongoing existence which is mysteriously unaffected by the passage of time, but because time has no connection with it. Whenever you look at it, it's the same, identical thing, not a later, miraculously preserved version of the thing.
What if 2 + 2 varies over something other than time that nonetheless correlates with time in our universe? Suppose 2 + 2 comes out to 4 the first 1 trillion times the operation is performed by humans, and to 5 on the 1 trillion and first time.
I suppose you could raise the same explanation: the definition of 2 + 2 makes no reference to how many times it has been applied. I believe the same can be said for any other reason you may give for why 2 + 2 might cease to equal 4.
Where that is the case, your method of mapping from the reality to arithmetic is not a good model of that process - no more, no less.
I'm not sure what the etiquette is of responding to retracted comments, but I'll have a go at this one.
Why is the same identical thing the same?
That's what I mean when I say they are identical. It's not another, separate thing, existing on a separate occasion, distinct from the first but standing in the relation of identity to it. In mathematics, you can step into the same river twice. Even aliens in distant galaxies step into the same river.
However, there is something else involved with the stability, which exists in time, and which is capable of being imperfectly stable: oneself. 2+2=4 is immutable, but my judgement that 2+2 equals 4 is mutable, because I change over time. If it seems impossible to become confused about 2+2=4, just think of degenerative brain diseases. Or being asleep and dreaming that 2+2 made 5.
The presentation of the natural numbers is meant to be standard, including the (well-known and proven) idea that it requires second-order logic to pin them down. There's some further controversy about second-order logic which will be discussed in a later post.
I've seen some (old) arguments about the meaning of axiomatizing which did not resolve in the answer, "Because otherwise you can't talk about numbers as opposed to something else," so AFAIK it's theoretically possible that I'm the first to spell out that idea in exactly that way, but it's an obvious-enough idea and there's been enough debate by philosophically inclined mathematicians that I would be genuinely surprised to find this was the case.
On the other hand, I've surely never seen a general account of meaningfulness which puts logical pinpointing alongside causal link-tracing to delineate two different kinds of correspondence within correspondence theories of truth. To whatever extent any of this is a standard position, it's not nearly widely-known enough or explicitly taught in those terms to general mathematicians outside model theory and mathematical logic, just like the standard position on "proof". Nor does any of it appear in the S. E. P. entry on meaning.
Very nice post!
Bug: Higher-order logic (a standard term) means "infinite-order logic" (not a standard term), not "logic of order greater 1" (also not a standard term). (For whatever reason, neither the Wikipedia nor the SEP entry seem to come out and say this, but every reference I can remember used the terms like that, and the usage in SEP seems to imply it too, e.g. "This second-order expressibility of the power-set operation permits the simulation of higher-order logic within second order.")
A few points:
i) you don't actually need to jump directly to second order logic in to get a categorical axiomatization of the natural numbers. There are several weaker ways to do the job: L_omega_omega (which allows infinitary conjunctions), adding a primitive finiteness operator, adding a primitive ancestral operator, allowing the omega rule (i.e. from the infinitely many premises P(0), P(1), ... P(n), ... infer AnP(n)). Second order logic is more powerful than these in that it gives a quasi categorical axiomatization of the universe of sets (i.e. of any two models of ZFC_2, they are either isomorphic or one is isomorphic to an initial segment of the other).
ii) although there is a minority view to the contrary, it's typically thought that going second order doesn't help with determinateness worries (i.e. roughly what you are talking about with regard to "pinning down" the natural numbers). The point here is that going second order only works if you interpret the second order quantifiers "fully", i.e. as ranging over the whole power set of the domain rather than some proper subset of it. But the problem is: how can we rule out non-full interpretations of the quan...
Thanks for posting this. My intended comments got pretty long, so I converted them to a blog post here. The gist is that I don't think you've solved the problem, partly because second order logic is not logic (as explained in my post) and partly because you are relying on a theorem (that second order Peano arithmetic has a unique model) which relies on set theory, so you have "solved" the problem of what it means for numbers to be "out there" only by reducing it to the question of what it means for sets to be "out there", which is, if anything, a greater mystery.
So this is where (one of the inspirations for) Eliezer's meta-ethics comes from! :)
A quick refresher from a former comment:
Cognitivism: Yes, moral propositions have truth-value, but not all people are talking about the same facts when they use words like "should", thus creating the illusion of disagreement.
... and now from this post:
Some people might dispute whether unicorns must be attracted to virgins, but since unicorns aren't real - since we aren't locating them within our universe using a causal reference - they'd just be talking about different models, rather than arguing about the properties of a known, fixed mathematical model.
(This little realization also holds a key to resolving the last meditation, I suppose.)
I've heard people say the meta-ethics sequence was more or less a failure since not that many people really understood it, but if these last posts were taken as a perequisite reading, it would be at least a bit easier to understand where Eliezer's coming from.
This is a really good post.
If I can bother your mathematical logician for just a moment...
Hey, are you conscious in the sense of being aware of your own awareness?
Also, now that Eliezer can't ethically deinstantiate you, I've got a few more questions =)
You've given a not-isomorphic-to-numbers model for all the prefixes of the axioms. That said, I'm still not clear on why we need the second-to-last axiom ("Zero is the only number which is not the successor of any number.") -- once you've got the final axiom (recursion), I can't seem to visualize any not-isomorphic-to-numbers models.
Also, how does one go about proving that a particular set of axioms has all its models isomorphic? The fact that I can't think of any alternatives is (obviously, given the above) not quite sufficient.
Oh, and I remember this story somebody on LW told, there were these numbers people talked about called...um, I'm just gonna call them mimsy numbers, and one day this mathematician comes to a seminar on mimsy numbers and presents a proof that all mimsy numbers have the Jaberwock property, and all the mathematicians nod and declare it a very fine finding, and then the next week, he comes back, and pre...
You just say: 'For every relation R that works exactly like addition, the following statement S is true about that relation.' It would look like, '∀ relations R: (∀x∀y∀z: R(x, 0, x) ∧ (R(x, y, z)→R(x, Sy, Sz))) → S)', where S says whatever you meant to say about +, using the token R.
The expression '(∀x∀y∀z: R(x, 0, x) ∧ (R(x, y, z)→R(x, Sy, Sz)))' is true for addition, but also for many other relations, such as a '∀x∀y∀z: R(x, y, z)' relation.
Yes, the educational goal of that paragraph is to "taboo addition". Nonetheless, the tabooing should be done correctly. If it is too difficult to do, then it is Eliezer's problem for choosing a difficult example to illustrate a concept.
This may sound like nitpicking, but this website has a goal is to teach people rationality skills, as opposed to "guessing the teacher's password". The article spends five screens explaining why details are so important when defining the concept of a "number", and the reader is supposed to understand it. So it's unfortunate if that explanation is followed by another example, which accidentally gets the similar details wrong. My objections against the wrong formula are very similar to the in-story mathematician's objections to the definitions of "number"; the definition is too wide.
Your suggestion: '∀x∀y∀z∀w: R(x, 0, x) ∧ (R(x, y, z)↔R(x, Sy, Sz)) ∧ ((R(x, y, z)∧R(x, y, w))→z=w)'
My alternative: '∀x∀y∀z: (R(x, 0, z)↔(x=z)) ∧ (R(x, y, z)↔R(x, Sy, Sz)) ∧ (R(x, y, z)↔R(Sx, y, Sz))'.
Both seem correct, and anyone knows a shorter (or a more legible) way to express it, please contribute.
Your idea of pinning down the natural numbers using second order logic is interesting, but I don't think that it really solves the problem. In particular, it shouldn't be enough to convince a formalist that the two of you are talking about the same natural numbers.
Even in second order PA, there will still be statements that are independent of the axioms, like "there doesn't exist a number corresponding to a Godel encoding of a proof that 0=S0 under the axioms of second order PA". Thus unless you are assuming full semantics (i.e. that for any collection of numbers there is a corresponding property), there should be distinct models of second order PA for which the veracity of the above statement differs.
Thus it seems to me that all you have done with your appeal to second order logic is to change my questions about "what is a number?" into questions about "what is a property?" In any case, I'm still not totally convinced that it is possible to pin down The Natural Numbers exactly.
How come we never see anything physical that behaves like any of of the non-standard models of first order PA? Given that's the case, it seems like we can communicate the idea of numbers to other humans or even aliens by saying "the only model of first order PA that ever shows up in reality", so we don't need second order logic (or the other logical ideas mentioned in the comments) just to talk about the natural numbers?
Yeah, but I've found the previous posts much more useful for coming up with clear explanations aimed at non-LWers, and I presume they'd make a better introduction to some of the core LW epistemic rationality than just throwing "The Simple Truth" at them.
You just say: 'For every relation R that works exactly like addition, the following statement S is true about that relation.' It would look like, '∀ relations R: (∀x∀y∀z: R(x, 0, x) ∧ (R(x, y, z)→R(x, Sy, Sz))) → S)', where S says whatever you meant to say about +, using the token R.
I would change the statement to be something other than 'S', say 'Q', as S is already used for 'successor'.
Requesting feedback:
..."Whenever a part of reality behaves in a way that conforms to the number-axioms - for example, if putting apples into a bowl obeys rules, like no apple spontaneously appearing or vanishing, which yields the high-level behavior of numbers - then all the mathematical theorems we proved valid in the universe of numbers can be imported back into reality. The conclusion isn't absolutely certain, because it's not absolutely certain that nobody will sneak in and steal an apple and change the physical bowl's behavior so that it doesn't m
Terry Tao's 2007 post on nonfirstorderizability and branching quantifiers gives an interesting view of the boundary between first- and second-order logic. Key quote:
...Moving on to a more complicated example, if Q(x,x’,y,y’) is a quaternary relation on four objects x,x’,y,y’, then we can express the statement
For every x and x’, there exists a y depending only on x and a y’ depending on x and x’ such that Q(x,x’,y,y’) is true
...but it seems that one cannot express
For every x and x’, there exists a y depending only on x and a y’ depending only on x’ such that
I'm a little confused as to which of two positions this is advocating:
Numbers are real, serious things, but the way that we pick them out is by having a categorical set of axioms. They're interesting to talk about because lots of things in the world behave like them (to some degree).
Mathematical talk is actually talk about what follows from certain axioms. This is interesting to talk about because lots of things obey the axioms and so exhibit the theorems (to some degree).
Both of these have some problems. The first one requires you to have weird, no...
Aye, right. Yer bum's oot the windae, laddie. Ye dinna need tae been lairnin a wee Scots tae unnerstan, it's gaein be awricht! Ane leid is enough.
Followup to: Causal Reference, Proofs, Implications and Models
The fact that one apple added to one apple invariably gives two apples helps in the teaching of arithmetic, but has no bearing on the truth of the proposition that 1 + 1 = 2.
-- James R. Newman, The World of Mathematics
Previous meditation 1: If we can only meaningfully talk about parts of the universe that can be pinned down by chains of cause and effect, where do we find the fact that 2 + 2 = 4? Or did I just make a meaningless noise, there? Or if you claim that "2 + 2 = 4"isn't meaningful or true, then what alternate property does the sentence "2 + 2 = 4" have which makes it so much more useful than the sentence "2 + 2 = 3"?
Previous meditation 2: It has been claimed that logic and mathematics is the study of which conclusions follow from which premises. But when we say that 2 + 2 = 4, are we really just assuming that? It seems like 2 + 2 = 4 was true well before anyone was around to assume it, that two apples equalled two apples before there was anyone to count them, and that we couldn't make it 5 just by assuming differently.
Speaking conventional English, we'd say the sentence 2 + 2 = 4 is "true", and anyone who put down "false" instead on a math-test would be marked wrong by the schoolteacher (and not without justice).
But what can make such a belief true, what is the belief about, what is the truth-condition of the belief which can make it true or alternatively false? The sentence '2 + 2 = 4' is true if and only if... what?
In the previous post I asserted that the study of logic is the study of which conclusions follow from which premises; and that although this sort of inevitable implication is sometimes called "true", it could more specifically be called "valid", since checking for inevitability seems quite different from comparing a belief to our own universe. And you could claim, accordingly, that "2 + 2 = 4" is 'valid' because it is an inevitable implication of the axioms of Peano Arithmetic.
And yet thinking about 2 + 2 = 4 doesn't really feel that way. Figuring out facts about the natural numbers doesn't feel like the operation of making up assumptions and then deducing conclusions from them. It feels like the numbers are just out there, and the only point of making up the axioms of Peano Arithmetic was to allow mathematicians to talk about them. The Peano axioms might have been convenient for deducing a set of theorems like 2 + 2 = 4, but really all of those theorems were true about numbers to begin with. Just like "The sky is blue" is true about the sky, regardless of whether it follows from any particular assumptions.
So comparison-to-a-standard does seem to be at work, just as with physical truth... and yet this notion of 2 + 2 = 4 seems different from "stuff that makes stuff happen". Numbers don't occupy space or time, they don't arrive in any order of cause and effect, there are no events in numberland.
Meditation: What are we talking about when we talk about numbers? We can't navigate to them by following causal connections - so how do we get there from here?
...
...
...
"Well," says the mathematical logician, "that's indeed a very important and interesting question - where are the numbers - but first, I have a question for you. What are these 'numbers' that you're talking about? I don't believe I've heard that word before."
Yes you have.
"No, I haven't. I'm not a typical mathematical logician; I was just created five minutes ago for the purposes of this conversation. So I genuinely don't know what numbers are."
But... you know, 0, 1, 2, 3...
"I don't recognize that 0 thingy - what is it? I'm not asking you to give an exact definition, I'm just trying to figure out what the heck you're talking about in the first place."
Um... okay... look, can I start by asking you to just take on faith that there are these thingies called 'numbers' and 0 is one of them?
"Of course! 0 is a number. I'm happy to believe that. Just to check that I understand correctly, that does mean there exists a number, right?"
Um, yes. And then I'll ask you to believe that we can take the successor of any number. So we can talk about the successor of 0, the successor of the successor of 0, and so on. Now 1 is the successor of 0, 2 is the successor of 1, 3 is the successor of 2, and so on indefinitely, because we can take the successor of any number -
"In other words, the successor of any number is also a number."
Exactly.
"And in a simple case - I'm just trying to visualize how things might work - we would have 2 equal to 0."
What? No, why would that be -
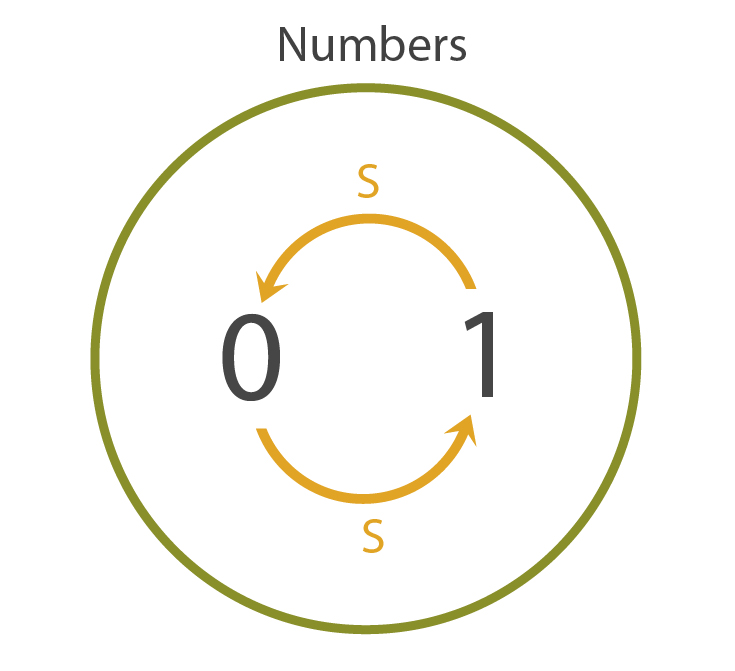
"I was visualizing a case where there were two numbers that were the successors of each other, so SS0 = 0. I mean, I could've visualized one number that was the successor of itself, but I didn't want to make things too trivial -"
No! That model you just drew - that's not a model of the numbers.
"Why not? I mean, what property do the numbers have that this model doesn't?"
Because, um... zero is not the successor of any number. Your model has a successor link from 1 to 0, and that's not allowed.
"I see! So we can't have SS0=0. But we could still have SSS0=S0."
What? How -
No! Because -
(consults textbook)
- if two numbers have the same successor, they are the same number, that's why! You can't have 2 and 0 both having 1 as a successor unless they're the same number, and if 2 was the same number as 0, then 1's successor would be 0, and that's not allowed! Because 0 is not the successor of any number!
"I see. Oh, wow, there's an awful lot of numbers, then. The first chain goes on forever."
It sounds like you're starting to get what I - wait. Hold on. What do you mean, the first chain -
"I mean, you said that there was at least one start of an infinite chain, called 0, but -"
I misspoke. Zero is the only number which is not the successor of any number.
"I see, so any other chains would either have to loop or go on forever in both directions."
Wha?
"You said that zero is the only number which is not the successor of any number, that the successor of every number is a number, and that if two numbers have the same successor they are the same number. So, following those rules, any successor-chains besides the one that start at 0 have to loop or go on forever in both directions -"
There aren't supposed to be any chains besides the one that starts at 0! Argh! And now you're going to ask me how to say that there shouldn't be any other chains, and I'm not a mathematician so I can't figure out exactly how to -
"Hold on! Calm down. I'm a mathematician, after all, so I can help you out. Like I said, I'm not trying to torment you here, just understand what you mean. You're right that it's not trivial to formalize your statement that there's only one successor-chain in the model. In fact, you can't say that at all inside what's called first-order logic. You have to jump to something called second-order logic that has some remarkably different properties (ha ha!) and make the statement there."
What the heck is second-order logic?
"It's the logic of properties! First-order logic lets you quantify over all objects - you can say that all objects are red, or all objects are blue, or '∀x: red(x)→¬blue(x)', and so on. Now, that 'red' and 'blue' we were just talking about - those are properties, functions which, applied to any object, yield either 'true' or 'false'. A property divides all objects into two classes, a class inside the property and a complementary class outside the property. So everything in the universe is either blue or not-blue, red or not-red, and so on. And then second-order logic lets you quantify over properties - instead of looking at particular objects and asking whether they're blue or red, we can talk about properties in general - quantify over all possible ways of sorting the objects in the universe into classes. We can say, 'For all properties P', not just, 'For all objects X'."
Okay, but what does that have to do with saying that there's only one chain of successors?
"To say that there's only one chain, you have to make the jump to second-order logic, and say that for all properties P, if P being true of a number implies P being true of the successor of that number, and P is true of 0, then P is true of all numbers."
Um... huh. That does sound reminiscent of something I remember hearing about Peano Arithmetic. But how does that solve the problem with chains of successors?
"Because if you had another separated chain, you could have a property P that was true all along the 0-chain, but false along the separated chain. And then P would be true of 0, true of the successor of any number of which it was true, and not true of all numbers."
I... huh. That's pretty neat, actually. You thought of that pretty fast, for somebody who's never heard of numbers.
"Thank you! I'm an imaginary fictionalized representation of a very fast mathematical reasoner."
Anyway, the next thing I want to talk about is addition. First, suppose that for every x, x + 0 = x. Next suppose that if x + y = z, then x + Sy = Sz -
"There's no need for that. We're done."
What do you mean, we're done?
"Every number has a successor. If two numbers have the same successor, they are the same number. There's a number 0, which is the only number that is not the successor of any other number. And every property true at 0, and for which P(Sx) is true whenever P(x) is true, is true of all numbers. In combination, those premises narrow down a single model in mathematical space, up to isomorphism. If you show me two models matching these requirements, I can perfectly map the objects and successor relations in them. You can't add any new object to the model, or subtract an object, without violating the axioms you've already given me. It's a uniquely identified mathematical collection, the objects and their structure completely pinned down. Ergo, there's no point in adding any more requirements. Any meaningful statement you can make about these 'numbers', as you've defined them, is already true or already false within that pinpointed model - its truth-value is already semantically implied by the axioms you used to talk about 'numbers' as opposed to something else. If the new axiom is already true, adding it won't change what the previous axioms semantically imply."
Whoa. But don't I have to define the + operation before I can talk about it?
"Not in second-order logic, which can quantify over relations as well as properties. You just say: 'For every relation R that works exactly like addition, the following statement Q is true about that relation.' It would look like, '∀ relations R: (∀x∀y∀z: (R(x, 0, z)↔(x=z)) ∧ (R(x, Sy, z)↔R(Sx, y, z))) → Q)', where Q says whatever you meant to say about +, using the token R. Oh, sure, it's more convenient to add + to the language, but that's a mere convenience - it doesn't change which facts you can prove. Or to say it outside the system: So long as I know what numbers are, you can just explain to me how to add them; that doesn't change which mathematical structure we're already talking about."
...Gosh. I think I see the idea now. It's not that 'axioms' are mathematicians asking for you to just assume some things about numbers that seem obvious but can't be proven. Rather, axioms pin down that we're talking about numbers as opposed to something else.
"Exactly. That's why the mathematical study of numbers is equivalent to the logical study of which conclusions follow inevitably from the number-axioms. When you formalize logic into syntax, and prove theorems like '2 + 2 = 4' by syntactically deriving new sentences from the axioms, you can safely infer that 2 + 2 = 4 is semantically implied within the mathematical universe that the axioms pin down. And there's no way to try to 'just study the numbers without assuming any axioms', because those axioms are how you can talk about numbers as opposed to something else. You can't take for granted that just because your mouth makes a sound 'NUM-burz', it's a meaningful sound. The axioms aren't things you're arbitrarily making up, or assuming for convenience-of-proof, about some pre-existent thing called numbers. You need axioms to pin down a mathematical universe before you can talk about it in the first place. The axioms are pinning down what the heck this 'NUM-burz' sound means in the first place - that your mouth is talking about 0, 1, 2, 3, and so on."
Could you also talk about unicorns that way?
"I suppose. Unicorns don't exist in reality - there's nothing in the world that behaves like that - but they could nonetheless be described using a consistent set of axioms, so that it would be valid if not quite true to say that if a unicorn would be attracted to Bob, then Bob must be a virgin. Some people might dispute whether unicorns must be attracted to virgins, but since unicorns aren't real - since we aren't locating them within our universe using a causal reference - they'd just be talking about different models, rather than arguing about the properties of a known, fixed mathematical model. The 'axioms' aren't making questionable guesses about some real physical unicorn, or even a mathematical unicorn-model that's already been pinpointed; they're just fictional premises that make the word 'unicorn' talk about something inside a story."
But when I put two apples into a bowl, and then put in another two apples, I get four apples back out, regardless of anything I assume or don't assume. I don't need any axioms at all to get four apples back out.
"Well, you do need axioms to talk about four, SSSS0, when you say that you got 'four' apples back out. That said, indeed your experienced outcome - what your eyes see - doesn't depend on what axioms you assume. But that's because the apples are behaving like numbers whether you believe in numbers or not!"
The apples are behaving like numbers? What do you mean? I thought numbers were this ethereal mathematical model that got pinpointed by axioms, not by looking at the real world.
"Whenever a part of reality behaves in a way that conforms to the number-axioms - for example, if putting apples into a bowl obeys rules, like no apple spontaneously appearing or vanishing, which yields the high-level behavior of numbers - then all the mathematical theorems we proved valid in the universe of numbers can be imported back into reality. The conclusion isn't absolutely certain, because it's not absolutely certain that nobody will sneak in and steal an apple and change the physical bowl's behavior so that it doesn't match the axioms any more. But so long as the premises are true, the conclusions are true; the conclusion can't fail unless a premise also failed. You get four apples in reality, because those apples behaving numerically isn't something you assume, it's something that's physically true. When two clouds collide and form a bigger cloud, on the other hand, they aren't behaving like integers, whether you assume they are or not."
But if the awesome hidden power of mathematical reasoning is to be imported into parts of reality that behave like math, why not reason about apples in the first place instead of these ethereal 'numbers'?
"Because you can prove once and for all that in any process which behaves like integers, 2 thingies + 2 thingies = 4 thingies. You can store this general fact, and recall the resulting prediction, for many different places inside reality where physical things behave in accordance with the number-axioms. Moreover, so long as we believe that a calculator behaves like numbers, pressing '2 + 2' on a calculator and getting '4' tells us that 2 + 2 = 4 is true of numbers and then to expect four apples in the bowl. It's not like anything fundamentally different from that is going on when we try to add 2 + 2 inside our own brains - all the information we get about these 'logical models' is coming from the observation of physical things that allegedly behave like their axioms, whether it's our neurally-patterned thought processes, or a calculator, or apples in a bowl."
I... think I need to consider this for a while.
"Be my guest! Oh, and if you run out of things to think about from what I've said already -"
Hold on.
"- try pondering this one. Why does 2 + 2 come out the same way each time? Never mind the question of why the laws of physics are stable - why is logic stable? Of course I can't imagine it being any other way, but that's not an explanation."
Are you sure you didn't just degenerate into talking bloody nonsense?
"Of course it's bloody nonsense. If I knew a way to think about the question that wasn't bloody nonsense, I would already know the answer."
Meditation for next time:
Humans need fantasy to be human.
"Tooth fairies? Hogfathers? Little—"
Yes. As practice. You have to start out learning to believe the little lies.
"So we can believe the big ones?"
Yes. Justice. Mercy. Duty. That sort of thing.
"They're not the same at all!"
You think so? Then take the universe and grind it down to the finest powder and sieve it through the finest sieve and then show me one atom of justice, one molecule of mercy.
- Susan and Death, in Hogfather by Terry Pratchett
So far we've talked about two kinds of meaningfulness and two ways that sentences can refer; a way of comparing to physical things found by following pinned-down causal links, and logical reference by comparison to models pinned-down by axioms. Is there anything else that can be meaningfully talked about? Where would you find justice, or mercy?
Mainstream status.
Part of the sequence Highly Advanced Epistemology 101 for Beginners
Next post: "Causal Universes"
Previous post: "Proofs, Implications, and Models"