Related to: Shane Legg on Prospect Theory and Computational Finance
This post is on prospect theory partly because it fits the theme of replacing simple utility functions with complicated reward functions, but mostly because somehow Less Wrong doesn't have any posts on prospect theory yet and that needs to change.
Kahneman and Tversky, the first researchers to identify and rigorously study cognitive biases, proved that a simple version of expected utility theory did not accurately describe human behavior. Their response was to develop prospect theory, a model of how people really make decisions. Although the math is less elegant than that of expected utility, and the shapes of the curves have to be experimentally derived, it is worth a look because it successfully predicts many of the standard biases.
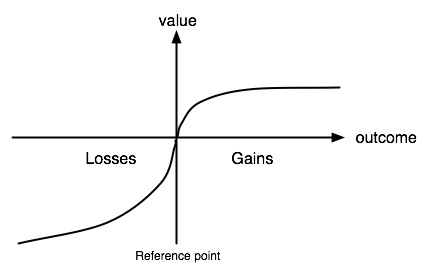
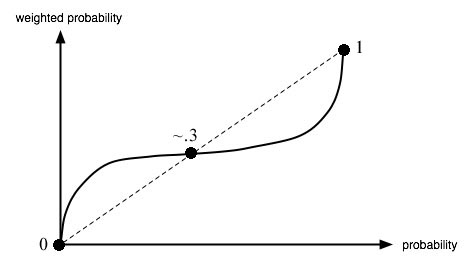
(source: Wikipedia)
A prospect theory agent tasked with a decision first sets it within a frame with a convenient zero point, allowing em to classify the results of the decision as either losses or gains. Ey then computes a subjective expected utility, where the subjective expected utility equals the subjective value times the subjective probability. The subjective value is calculated from the real value using a value function similar to the one on the left-hand graph, and the subjective probability is calculated from the real probability using a weighting function similar to the one on the right-hand graph.
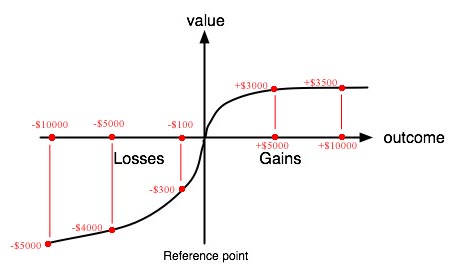
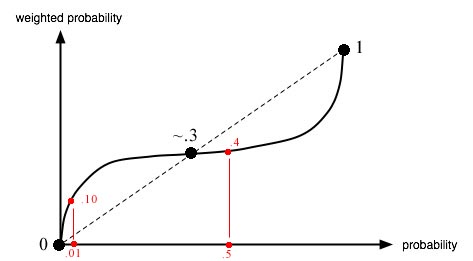
Clear as mud? Let's fill some numbers into the functions - the exact assignments don't really matter as long as we capture the spirit of where things change steeply versus slowly - and run through an example.
Imagine a prospect theory agent - let's call him Prospero - trying to decide whether or not to buy an hurricane insurance policy costing $5000/year. Prospero owns assets worth $10,000, and estimates a 50%/year chance of a hurricane destroying his assets; to make things simple, he will be moving in one year and so need not consider the future. Under expected utility theory, he should feel neutral about the policy.
Under prospect theory, he first sets a frame in which to consider the decision; his current state is a natural frame, so we'll go with that.
We see on the left-hand graph that an objective $10,000 loss feels like a $5,000 loss, and an objective $5000 loss feels like a $4000 loss. And we see on the right-hand graph that a 50% probability feels like a 40% probability.
Now Prospero's choice is a certain $4000 loss if he buys the insurance, versus a 40% chance of a $5000 loss if he doesn't. Buying has a subjective expected utility of -$4000; not buying has a subjective expected utility of -$2000. So Prospero decisively rejects the insurance.
But suppose Prospero is fatalistic; he views his assets as already having been blown away. Here he might choose a different frame: the frame in which he starts with zero assets, and anything beyond that is viewed as a gain.
Since the gain half of the value function levels off more quickly than the loss half, $5000 is now subjectively worth $3000, and $10000 is now subjectively worth $3500.
Here he must choose between a certain gain of $5000 and a 50% chance of gaining $10000. Expected utility gives the same result as before, obviously. In prospect theory, he chooses between a certain subjective gain of $3000 and a 40% chance of gaining $3500. The insurance gives him subjective expected utility of $3000, and rejecting it gives him subjective expected utility of $1400.
All of a sudden Prospero wants the insurance.
We notice the opposite effect if there is only a a 1% chance of a hurricane. The insurance salesman lowers his price to $100 to preserve the neutrality of the insurance option when using utility.
But subjective probability rises very quickly, so a 1% chance may correspond to a subjective 10% chance. Now in the first frame, Prospero must decide between an objective loss of -$100 with certainty (corresponding to -$300 subjective since the value function is steeper closer to zero) or an objective loss of -$10,000 with objective probability 1% (subjective of 10%). Now the expected subjective utilities are -$300 if he buys, versus -$500 if he rejects. And so he buys the insurance. When we change the risk of hurricane from 50% to 1%, then even though we reduce the price of the insurance by an exactly equal amount, Prospero's decision switches from not buying to buying.
Let's see how many previously discussed biases we can fit into this model.
Prospero's change from rejecting the insurance when framed as gains, to buying it when framed as losses, directly mirrors the change in preferred survival strategies mentioned in Circular Altruism.
The necessity of frame-shifting between different perceptions of losses also produces the Sunk Cost Fallacy.
The greater steepness of the value function with losses as opposed to gains is not even an explanation for, but merely a mathematical representation of, loss aversion.
The leveling off of the value function that turned the huge objective difference between +$5000 and +$10000 into the teensy little subjective difference between +$3000 and +$3500 mirrors the scope insensitivity under which people show about the same level of interest in proposals to save endangered birds whether a thousand, ten thousand, or a hundred thousand birds are involved.
It may not be an official bias, but the "but there's still a chance, right" outlook looks a lot like the sharply rising curve of the subjective probability function near zero.
And although it is not immediately obvious from the theory, some people want to link the idea of a frame to priming and anchoring-adjustment, on the grounds that when a suitable reference frame doesn't exist any primed stimulus can help establish one.
And now, the twist: prospect theory probably isn't exactly true. Although it holds up well in experiments where subjects are asked to make hypothetical choices, it may fare less well in the rare experiments where researchers can afford to offer subjects choices for real money (this isn't the best paper out there, but it's one I could find freely available).
Nevertheless, prospect theory seems fundamentally closer to the mark than simple expected utility theory, and if any model is ever created that can explain both hypothetical and real choices, I would be very surprised if at least part of it did not involve something looking a lot like Kahneman and Tversky's model.