Sometime during the 1740s, the Reverend Thomas Bayes made the ingenious discovery that bears his name but then mysteriously abandoned it. It was rediscovered independently by a different and far more renowned man, Pierre Simon Laplace, who gave it its modern mathematical form and scientific application — and then moved on to other methods. Although Bayes’ rule drew the attention of the greatest statisticians of the twentieth century, some of them vilified both the method and its adherents, crushed it, and declared it dead. Yet at the same time, it solved practical questions that were unanswerable by any other means: the defenders of Captain Dreyfus used it to demonstrate his innocence; insurance actuaries used it to set rates; Alan Turing used it to decode the German Enigma cipher and arguably save the Allies from losing the Second World War; the U.S. Navy used it to search for a missing H-bomb and to locate Soviet subs; RAND Corporation used it to assess the likelihood of a nuclear accident; and Harvard and Chicago researchers used it to verify the authorship of the Federalist Papers. In discovering its value for science, many supporters underwent a near-religious conversion yet had to conceal their use of Bayes’ rule and pretend they employed something else. It was not until the twenty-first century that the method lost its stigma and was widely and enthusiastically embraced.
So begins Sharon McGrayne's fun new book, The Theory That Would Not Die, a popular history of Bayes' Theorem. Instead of reviewing the book, I'll summarize some of its content below. I skip the details and many great stories from the book, for example the (Bayesian) search for a lost submarine that inspired Hunt for Red October. Also see McGrayne's Google Talk here. She will be speaking at the upcoming Singularity Summit, too, which you can register for here (price goes up after August 31st).
Origins
In the 1700s, when probability theory was just a whiff in the air, the English Reverend Thomas Bayes wanted to know how to infer causes from effects. He set up his working problem like this: How could he learn the probability of a future event occurring if he only knew how many times it had occurred or not occurred in the past?
He needed a number, and it was hard to decide which number to choose. In the end, his solution was to just guess and then improve his guess later as he gathered more information.
He used a thought experiment to illustrate the process. Imagine that Bayes has his back turned to a table, and he asks his assistant to drop a ball on the table. The table is such that the ball has just as much chance of landing at any one place on the table as anywhere else. Now Bayes has to figure out where the ball is, without looking.
He asks his assistant to throw another ball on the table and report whether it is to the left or the right of the first ball. If the new ball landed to the left of the first ball, then the first ball is more likely to be on the right side of the table than the left side. He asks his assistant to throw the second ball again. If it again lands to the left of the first ball, then the first ball is even more likely than before to be on the right side of the table. And so on.
Throw after throw, Bayes is able to narrow down the area in which the first ball probably sits. Each new piece of information constrains the area where the first ball probably is.
Bayes' system was: Initial Belief + New Data -> Improved Belief.
Or, as the terms came to be called: Prior + Likelihood of your new observation given competing hypotheses -> Posterior.
In each new round of belief updating, the most recent posterior becomes the prior for the new calculation.
There were two enduring criticisms to Bayes' system. First, mathematicians were horrified to see something as whimsical as a guess play a role in rigorous mathematics. Second, Bayes said that if he didn't know what guess to make, he'd just assign all possibilities equal probability to start. For most mathematicians, this problem of priors was insurmountable.
Bayes never published his discovery, but his friend Richard Price found it among his notes after Bayes' death in 1761, re-edited it, and published it. Unfortunately, virtually no one seems to have read the paper, and Bayes' method lay cold until the arrival of Laplace.
Laplace
By the late 18th century, Europe was awash in scientific data. Astronomers had observations made by the Chinese in 1100 BC, by the Greeks in 200 BC, by the Romans in AD 100, and by the Arabs in AD 1000. The data were not of equal reliability. How could scientists process all their observations and choose the best? Many astronomers simply averaged their three 'best' observations, but this was ad-hoc. The world needed a better way to handle all these data.
Pierre-Simon Laplace, a brilliant young mathematician, came to believe that probability theory held the key, and he independently rediscovered Bayes' mechanism and published it in 1774. Laplace stated the principle not with an equation, but in words: the probability of a cause (given an event) is proportional to the probability of the event (given its cause). And for the next 40 years, Laplace used, extended, clarified, and proved his new principle.
In 1781, Richard Price visited Paris, and word of Bayes' earlier discovery eventually reached Laplace. Laplace was now all the more confident that he was on the right track.
He needed to test his principle, so he turned to the largest data set available: birth records. A few people had noticed that slightly more boys than girls were born, and Laplace wanted to know if this was an anomalous or constant phenomenon. He began by applying equal probability to his hunches, and then updated his belief as he examined data sets from Paris, from London, from Naples, from St. Petersburg, and from rural areas in France. Later he even asked friends for birth data from Egypt and Central America. Finally, by 1812, he was almost certain that the birth of more boys than girls was "a general law for the human race."
Laplace's friend Bouvard used his method to calculate the masses of Jupiter and Saturn from a wide variety of observations. Laplace was so impressed that he offered his readers a famous bet: 11,000 to 1 odds that Bouvard's results for Saturn were within 1% of the correct answer, and a million to one odds for Jupiter. Nobody seems to have taken Laplace's bet, but today's technology confirms that Laplace should have won both bets.
Laplace used his principle on the issue of testimony, both in court and in the Bible, and made famous progress in astronomy. When asked by Napoleon who authored the heavens, Laplace replied that natural law could explain the behavior of the heavens. Napoleon asked why Laplace had failed to mention God in his book on the subject. Laplace replied: "Sire, I have no need of that hypothesis."
The answer became a symbol of the new science: the search for natural laws that produced phenomena without the need to call upon magic in the explanation.
And then, Laplace invented the central limit theorem, which let him handle almost any kind of data. He soon realized that where large amounts of data were available, both the Bayesian and the frequentist approaches (judging an event's probability by how frequently it occurs among many observations) to probability tended to produce the same results. (Only much later did scientists discover how wildly the two approaches can diverge even given lots of data.)
And so at age 62, Laplace — the world's first Bayesian — converted to frequentism, which he used for the remaining 16 years of his life.
...though he did finally realize what the general theorem for Bayes' method had to be:
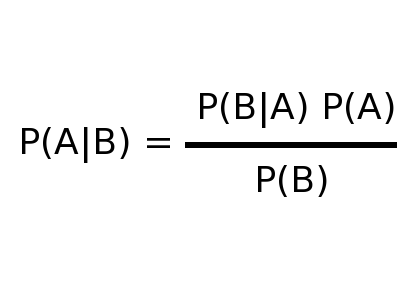
P(C|E) = [ P(E|C)Pprior(C) ] / [ΣP(E|C')Pprior(C')
Which says that the probability of a hypothesis C given some evidence E equals our initial estimate of the probability times the probability of the evidence given the hypothesis C divided by the sum of the probabilities of the data in all possible hypotheses.
Basically, Laplace did all the hard work, and he deserves most of the honor for what we call Bayes' Theorem. But historical accidents happen, and the method is named after Bayes.
The Decline of Bayes' Theorem
Empowered by Laplace's central limit theorem, government officials were expected to collect statistics on all sorts of things: cholera victims, the chest sizes of soldiers, the number of Prussian officers killed by kicking horses, and so on. But the idea that probability quantifies our ignorance was gone, replaced by the idea that the new science could not allow for anything 'subjective'. John Stuart Mill denounced probability as "ignorance... coined into science."
By 1891, the Scottish mathematician George Chrystal urged: "[Laplace's principle] being dead, [it] should be decently buried out of sight, and not embalmed in text-books and examination papers... The indiscretions of great men should be quietly allowed to be forgotten."
And thus, Bayes' Theorem fell yet again in disuse... at least among theoreticians. A smattering of practitioners continued to find it useful.
Joseph Bertrand was convinced that Bayes' Theorem was the only way for artillery officers to correctly deal with a host of uncertainties about the enemies' location, air density, wind direction, and more. From 1890-1935, French and Russian artillery officers used Bertrand's Bayesian textbook to fire their weapons.
When the French Jew Alfred Dreyfus was falsely accused of having sold a letter to German military expert, France's famous mathematician Henri Poincaré was called to the stand. Poincaré was a frequentist, but when asked whether Dreyfus had written the letter, Poincaré invoked Bayes' Theorem as the only sensible way for a court of law to update a hypothesis with new evidence, and proclaimed that the prosecution's discussion of probability was nonsense. Dreyfus was still convicted, though his sentence was reduced, but the public was outraged and the president issued a pardon two weeks later.
Statisticians used Bayes' Theorem to set up a functioning Bell phone system, set of up the United States' first working social insurance system, and solve other problems.
Meanwhile, the biologist R.A. Fisher was pioneering new randomization methods, sampling theory, tests of significant, analyses of variance, and a variety of experimental designs. In 1925 he published his revolutionary manual, Statistical Methods of Research Workers. The success of the book enshrined frequentism and the standard statistical method.
Jeffreys
Even during its decline, a few people made progress on Bayesian theory. At about the same time, three men in three countries — Émile Borel, Frank Ramsey, and Bruno de Finetti — independently happened upon the same idea: knowledge is subjective, and we can quantify it with a bet. The amount we wager shows how strongly we believe something.
And then, the geologist Harold Jeffreys made Bayes' Theorem useful for scientists, proposing it as an alternative to Fisher's 'p-values' and 'significance tests', which depended on "imaginary repetitions." In contrast, Bayesianism considered data as fixed evidence. Moreover, the p-value is a statement about data, but Jeffreys wanted to know about his hypothesis given the data. He published the monumental Theory of Probability in 1939, which remained for many years the only explanation of how to use Bayes to do science.
For decades, Fisher and Jeffreys were the world's two greatest statisticians, though both were practicing scientists instead of theoreticians. They traded blows over probability theory in scientific journals and in public. Fisher was louder and bolder, and frequentism was easier to use than Bayesianism.
Bayes at War
In 1941, German U-Boats were devastating allied naval forces. Britain was cut off from its sources of food, and couldn't grow enough on its own soil to feed its citizens. Winston Churchill said the U-boat problem was the scariest part of the war for him.
The German codes, produced by Enigma machines with customizable wheel positions that allowed the codes to be changed rapidly, were considered unbreakable, so nobody was working on them. This attracted Alan Turing to the problem, because he liked solitude. He built a machine that could test different code possibilities, but it was slow. The machine might need four days to test all 336 wheel positions on a particular Enigma code. Until more machines could be built, Turing had to find a way for reducing the burden on the machine.
He used a Bayesian system to guess the letters in an Enigma message, and add more clues as they arrived with new data. With this method he could reduce the number of wheel settings to be tested by his machine from 336 to as few as 18. But soon, Turing realized that he couldn't compare the probabilities of his hunches without a standard unit of measurement. So, he invented the 'ban', defined as "about the smallest change in weight of evidence that is directly perceptible to human intuition." This unit turned out to be very similar to the bit, the measure of information discovered using Bayes' Theorem while working for Bell Telephone.
Now that he had a unit of measurement, he could target the amount of evidence he needed for a particular hunch and then stop the process when he had that much evidence.
While Turing was cracking the Enigma codes in Britain, Andrey Kolmogorov was fleeing the German artillery bombardment of Moscow. In 1933 he had showed that probability theory can be derived from basic mathematical axioms, and now Russia's generals were asking him about how best to fire back at the Germans. Though a frequentist, Kolmogorov recommended they used Bertrand's Bayesian firing system in a crisis like this.
Shortly after this, the British learned that the Germans were now using stronger, faster encryption machines: Lorenz machines. The British team used Turing's Bayesian scoring system and tried a variety of priors to crack the codes.
Turing visited America and spent time with Claude Shannon, whose brilliant insights about information theory came a bit later. He realized that the purpose of information is to reduce uncertainty and the purpose of encryption is to increase it. He was using Bayes for both. Basically, if the posterior in a Bayesian equation is very different from the prior, then much has been learned, but if the posterior is roughly the same as the prior, then the information content is low. Shannon's unit for information was the 'bit'.
Meanwhile, Allied patrol planes needed to narrow their search for German U-boats. If 7 different listening posts intercepted the same message from the same U-boat, it could be located to somewhere in a circle 236 miles across. That's a lot of uncertainty, and mathematician Bernard Koopman was assigned to solve the problem. He wasn't bashful about Bayes at all. He said: "Every operation involved in search is beset with uncertainties; it can be understood quantitatively only in terms of... probability. This may now be regarded as a truism, but it seems to have taken the developments in operational research of the Second World War to drive home its practical implications."
Koopman started by assigning 50% probability that a U-boat was inside the 236-mile circle, and then update his probability as more data came in, apportioning plane flyover hours according to the probabilities of U-boat locations.
And then, a few day's after Germany's surrender, Churchill ordered the destruction of all evidence that decoding has helped win the war, apparently because the British didn't want the Soviets to know they could decrypt Lorenz codes. It wasn't until 1973 that the story of Turing and Bayes began to emerge.
Revival
Its wartime successes classified, Bayes' Theorem remained mostly in the dark after the Second World War. Textbooks self-righteously dismissed Bayes. During the McCarthyism of the 1950s, one government statistician half-jokingly called a colleague "un-American because [he] was a Bayesian, ...undermining the United States Government."
In 1950, an economist preparing a report asked statistician David Blackwell (not yet a Bayesian) to estimate the probability of another world war in the next five years. Blackwell answered: "Oh, that question just doesn't make sense. Probability applies to a long sequence of repeatable events, and this is clearly a unique situation. The probability is either 0 or 1, but we won't know for five years." The economist replied, "I was afraid you were going to say that. I've spoken to several other statisticians, and they all told me the same thing."
Still, there were flickers of life. For decades after the war, one of Turing's American colleagues taught Bayes to NSA cryptographers. I.J. Good, one of Turing's statistics assistant, developed Bayesian methods and theory, writing about 900 articles about Bayes.
And then there was the Bible-quoting business executive Arthur Bailey.
Bailey was trained in statistics, and when he joined an insurance company he was horrified to see them using Bayesian techniques developed in 1918. They asked not "What should the new rates be?" but instead "How much should the present rates be changed?" But after a year of trying different things, he realized that the Bayesian actuarial methods worked better than frequentist methods. Bailey "realized that the hard-shelled underwriters were recognizing certain facts of life neglected by the statistical theorists." For example, Fisher's method of maximum likelihood assigned a zero probability to nonevents. But since many businesses don't file insurance claims, Fisher's method produced premiums that were too low to cover future costs.
Bailey began writing a paper about his change in attitude about Bayes. By 1950 he was vice president of a large insurance company in Chicago. On May 22 he read his famous paper at a black-tie banquet for an actuarial society. The title: 'Credibility Procedures: Laplace's Generalization of Bayes' Rule and the Combination of [Prior] Knowledge with Observed Data.'
Bailey praised his colleagues for standing mostly alone against the statistics establishment. Then he announced that their beloved Credibility formula was actually Bayes Theorem, and in fact that the person who had published Bayes' work, Richard Price, would today be considered an actuary. He used Bayes' ball-and-table thought experiment to attack Fisher and his methods, and ended with a rousing call to put prior knowledge back into probability theory. His speech occupied theorists for years, and actuaries often see Bailey as taking their profession out of its dark ages.
That same year, I.J. Good published Probability and the Weighing of Evidence, which helped to found Bayes' Theorem into a logical, coherent methodology. Good was smart, quick, and by now perhaps the world's expert on codes. He introduced by holding out his hand and saying "I am Good." When the British finally declassified his cryptanalysis work, allowing him to reveal Bayes' success during WWII, he bought a vanity licensed plate reading 007 IJG.
In the 1950s, Dennis Lindley and Jimmie Savage worked to turn the statistician's hodgepodge of tools into a "respectable branch of mathematics," as Kolmogorov had done for probability in in general in the 1930s. They found some success at putting statistics on a rigorous mathematical footing, and didn't realize at the time that they couldn't get from their theorems to the ad hoc methods of frequentism. Lindley said later, "We were both fools because we failed completely to recognize the consequences of what we were doing."
In 1954, Savage published Foundations of Statistics, which built on Frank Ramsey's earlier attempts to use Bayes' Theorem not just for making inferences but for making decisions, too. His response to a classic objection to Bayesianism is worth remembering. He was asked, "If prior opinions can differ from one researcher to the next, what happens to scientific objectivity in data analysis?" Savage explained that as we gain data, subjectivists move into agreement, just as scientists come to consensus as evidence accumulates about, say, cigarettes causing lung cancer. When they have little data, scientists are subjectivists. When they have tons of data, they agree and become objectivists.
Savage became a Messianic advocate of Bayesianism, but died suddenly of a heart attack in 1971. I.J. Good was active but working at a small university and was poor at public speaking. David Lindley, however, moved to Britain and almost single-handedly created 10 Bayesian departments in the U.K. — professorship by professorship, battle by battle, he got Bayesians hired again and again. By 1977 he was exhausted and retired early.
Medicine
In 1951, history major Jerome Cornfield used Bayes' Theorem to solve a puzzle about the chances of a person getting lung cancer. His paper helped epidemiologists to see how patients' histories could help measure the link between a disease and its possible cause. Moreover, he had begun to establish the link between smoking and lung cancer. Later efforts in England and the U.S. confirmed Cornfield's results.
Fisher and Neyman, the world's two leading anti-Bayesians, didn't accept the research showing that cigarettes caused lung cancer. Fisher, especially, published many papers. He even developed the hypothesis that, somehow, lung cancer might cause smoking. But in 1959, Cornfield published a paper that systematically addressed every one of Fisher's arguments, and Fisher ended up looking ridiculous.
Cornfield went on to be involved in most of the major public health battles involving scientific data and statistics, and in 1974 was elected president of the American Statistical Association despite never having gotten any degree in statistics. He had developed a congenial spirit and infectious laugh, which came in handy when enduring long, bitter battles over health issues.
In 1979 he was diagnosed with pancreatic cancer, but his humor remained. A friend told him, "I'm so glad to see you." Smiling, Cornfield replied, "That's nothing compared to how happy I am to be able to see you." As he lay dying, he called to his two daughters and told them: "You spend your whole life practicing humor for the times when you really need it."
Practical Use
Frequentist methods worked for repetitive, standardized phenomena like crops, genetics, gambling, and insurance. But business executives needed to make decisions under conditions of uncertainty, without sample data. And frequentism didn't address that problem.
At Harvard Business School, Robert Schlaifer thought about the problem. He realized that starting with prior information about demand for a product was better than nothing. From there, he realized that he could update his prior with new evidence, and independently arrived at Bayes' Theorem. Unaware of the literature, he reinvented Bayesian decision theory from scratch and began to teach it confidently. He did not think of it as 'an' approach. It was the approach, and everybody else was wrong, and he could show everybody else why they were wrong.
Later, he recruited Howard Raiffa to come work with him, because he needed another Bayesian to teach him more math. Together, the two invented the field of Decision-making Under Uncertainty (DUU). Schlaifer wrote the first practical textbook written entirely from a Bayesian perspective: Probability and Statistics for Business Decisions (1959). They introduced useful tools like decision trees, 'tree-flipping', and conjugate priors. They co-authored what would become the standard textbook of Bayesian statistics for two decades: Applied Statistical Decision Theory. Today, Bayesian methods dominate the business decision-making literature but frequentists still have some hold on statistics departments.
Meanwhile, Frederick Mosteller spent a decade using early computers and hundreds of volunteers to painstakingly perform a Bayesian analysis of the disputed Federalist Papers, and concluded with high probability that they were all written by Madison, not Hamilton. The work impressed many statisticians, even frequentists.
Bayes had another chance at fame during the 1960 presidential race between Nixon and Kennedy. The race was too close to call, but the three major TV networks all wanted to be the first to make the correct call. NBC went looking for someone to help them predict the winner, and they found Princeton statistics professor John Tukey. Tukey analyzed huge amounts of voting data, and by 2:30am during the election Tukey and his colleagues were ready to call Kennedy as the winner. The pressure was too much for NBC to make the call, though, so they locked Tukey and his team in a room until 8am when it was clear Kennedy was indeed the winner. NBC immediately asked him to come back for the 1962 election, and Tukey worked with NBC for 18 years.
But Tukey publicly denied Bayesianism. When working on the NBC projects, he said he wasn't using Bayes, instead he was "borrowing strength." He didn't allow anybody on his team to talk about their methods, either, saying it was proprietary information.
In 1980 NBC soon switched to exit polling to predict elections. Exit polling was more visual, chatty, and fun than equations. It would be 28 years before someone used Bayes to predict presidential election results. When Nate Silver of FiveThirtyEight.com used Bayes to predict results of the November 2008 race, he correctly predicted the winner in 49 states, an unmatched record among pollsters.
When the U.S. Atomic Energy Commission ordered a safety study of nuclear power plants, they hired Norman Rasmussen. At the time, there had never been a nuclear power plant accident. He couldn't use frequentist methods to estimate the probability of something that had never happened. So he looked to two sources: equipment failure rates, and expert opinion. But how could he combine those two types of evidence?
Bayes' Theorem, of course. But Rasmussen knew that Bayes was so out of favor that his results would be dismissed by the statistics community if he used the word 'Bayes'. So he used Raiffa's decision trees, instead. They were grounded in Bayes, but this way he didn't have to use the word 'Bayes.'
Alas, the report's subjectivist approach to statistics was roundly damned, and the U.S. Nuclear Regulatory Commission withdrew its support for the study five years later. And two months after they did so, the Three Mile Island accident occurred.
Previous experts had said the odds of severe core damage were extremely low, but the effects would be catastrophic. Instead, the Rasmussen report had concluded that the probability of core damage was higher than anticipated, but the consequences wouldn't be catastrophic. The report also identified two important sources of the problem: human error and radioactivity outside the building. In the eyes of many, the report had been vindicated.
Finally, in 1983 the US Air Force sponsored a review of NASA's estimates of the probability of shuttle failure. NASA's estimate was 1 in 100,000. The contractor used Bayes and estimated the odds of rocket booster failure at 1 in 35. In 1986, Challenger exploded.
Victory
Adrian Raftery examined a set of statistics about coal-dust explosions in 19th-century British mines. Frequentist techniques had shown the coal mining accident rates changed over time gradually. Our of curiosity, Raftery experimented with Bayes' Theorem, and discovered that accident rates had plummeted suddenly in the early 1890s. A historian suggested why: in 1889, the miners had formed a safety coalition.
Frequentist statistics worked okay when one hypothesis was a special case of another, but when hypotheses were competing and abrupt changes were in the data, frequentism didn't work. Many sociologists were ready to give up on p-values already, and Raftery's short 1986 paper on his success with Bayes led many sociologists to jump ship to Bayesianism. Raftery's paper is now one of the most cited in sociology.
One challenge had always been that Bayesian statistical operations were harder to calculate, and computers were still quite slow. This changed in the 90s, when computers became much faster and cheaper than before, and especially with the invention of the Markov Chain Monte Carlo method, which suddenly allowed Bayesians to do a lot more than frequentists can. The BUGS program also helped.
These advances launched the 'Bayesian revolution' in a long list of fields: medical diagnosis, ecology, geology, computer science, artificial intelligence, machine learning, genetics, astrophysics, archaeology, psychometrics, education performance, sports modeling, and more. This is only partly because Bayes' Theorem shows us the mathematically correct response to new evidence. It is also because Bayes' Theorem works.

