Article on IQ: The Inappropriately Excluded
13Douglas_Knight
2James_Miller
8Douglas_Knight
4James_Miller
2Val
4Houshalter
0Good_Burning_Plastic
1Houshalter
0buybuydandavis
2Douglas_Knight
11J Bostock
11Dagon
8buybuydandavis
9gwern
2buybuydandavis
6moridinamael
17gwern
9James_Miller
13gwern
0ChristianKl
5hg00
2buybuydandavis
3Lumifer
2Elizabeth
2ChristianKl
2Document
2ChristianKl
5gwern
0ChristianKl
1Jay
8gwern
1Jay
0MichaelWFerguson
8gjm
1Jay
7gjm
New Comment
First of all, IQ tests aren't designed for high IQ, so there's a lot of noise there and this would mainly be noise, if he correctly reported the results, which he doesn't.
Second, there are some careful studies of high IQ (SMPY etc) by taking the well designed SAT test, which doesn't have a very high ceiling for adults and giving it to children below the age of 13. By giving the test to representative samples, they can well characterize the threshold for the top 3%. Using self-selected samples, they think that they can characterize up to 1/10,000. In any event, within the 3% they find increasing SAT score predicts increasing probability of accomplishments of all kinds, in direct contradiction of these claims.
IQ tests aren't designed for high IQ,
But they might work on children with high IQs because you can compare their performance to older children. A genius 8-year-old does as well as a typical 14-year old, whereas a super-genius 8-year-old does as well as a 16 year old.
Doesn't that sound like my second paragraph?
But there is an assumption here, that childhood IQ predicts adult IQ. In fact, it isn't very good at age 8. The SMPY age of 12 is better, though by no means perfect. When I say "good" or "better" I mean, of course, stability at the center, which might not predict stability at the tails. When SMPY finds that age 12 tests predict life outcomes, they are testing this directly. But what we really want to know is whether the SAT score at age 12 adds information to the low ceiling SAT score at age 17. I think that the SMPY results are strong enough to guarantee that, but I haven't checked.
Doesn't that sound like my second paragraph?
Yes, my error.
But what we really want to know is whether the SAT score at age 12 adds information to the low ceiling SAT score at age 17.
For testing error/randomness reasons you would think so even independent of the low ceiling problem.
First of all, IQ tests aren't designed for high IQ, so there's a lot of noise there and this is probably mainly noise.
Indeed. If an IQ test claims to provide accurate scores outside of the 70 to 130 range, you should be suspicious.
There are so many misunderstandings about IQ in the general population, ranging from claims like "the average IQ is now x" (where x is different from 100), to claims of a famous scientist having had an IQ score over 200, and claims of "some scientists estimating" the IQ of a computer, an animal, or a fictional alien species. Or things as simple as claiming to calculate an IQ score based on a low number (usually less than 10) of trivia questions about basic geography and names of celebrities.
"the average IQ is now x" (where x is different from 100)
I think you are just being pedantic. When people say something like "the flynn effect has raised the average IQ has increased by 10 points over the last 50 years", they mean that the average person would score 10 points higher on a 1950's IQ test. See also the value of money, which also changes over time due to inflation. When people say "a dollar was worth more 50 years ago", you don't reply "nuh uh, a dollar has always been worth exactly one dollar."
claims of "some scientists estimating" the IQ of a computer, an animal, or a fictional alien species.
I mean it's impossible to do any kind of serious estimate. But I don't think the idea of a linear scale of intelligence is inherently meaningless. So you could give a very rough estimate where nonhuman intelligences would fall on it, and where that would put them relative to humans with such and such IQ.
When people say "a dollar was worth more 50 years ago", you don't reply "nuh uh, a dollar has always been worth exactly one dollar."
Yes, but "a dollar is now worth $x" where x is different from 1 is still meaningless unless you specify you're talking about today's dollar vs some other year's dollar specifically.
That's correct, but usually I don't see that mistake made about IQ. On a handful of occasions I've seen someone say "we could raise the average IQ by 10 points" or something like that, and some pedant responds that "the average IQ must always be 100". Which is technically correct, but misses the point. It makes it difficult to have discussions about IQ over time.
Accomplishments?
Did that include being a part of an elite profession?
I think the original article said that smart people accomplished more in a profession, though they were in appropriately excluded.
I think that the main accomplishments studied were degrees, advanced degrees, published academic articles articles, books published, and patents. I believe that they also looked at postdocs and professorships. The article only presented confused data on two professions: professors and physicians. MDs are a very good proxy for being a physician, so SMPY has that covered, too.
Edit: It appears I have basically just said what Gwern said but with graphs.
I can't work out what they're doing with their statistics to get the numbers they claim, because they don't show their working. I have however seen a very similar article which used the same data. In that case I believe the error came from assuming a normal distribution of intelligence in the overall population and in the faculty population.
Here are a couple of graphs I have thrown together to demonstrate what I suspect has happened:
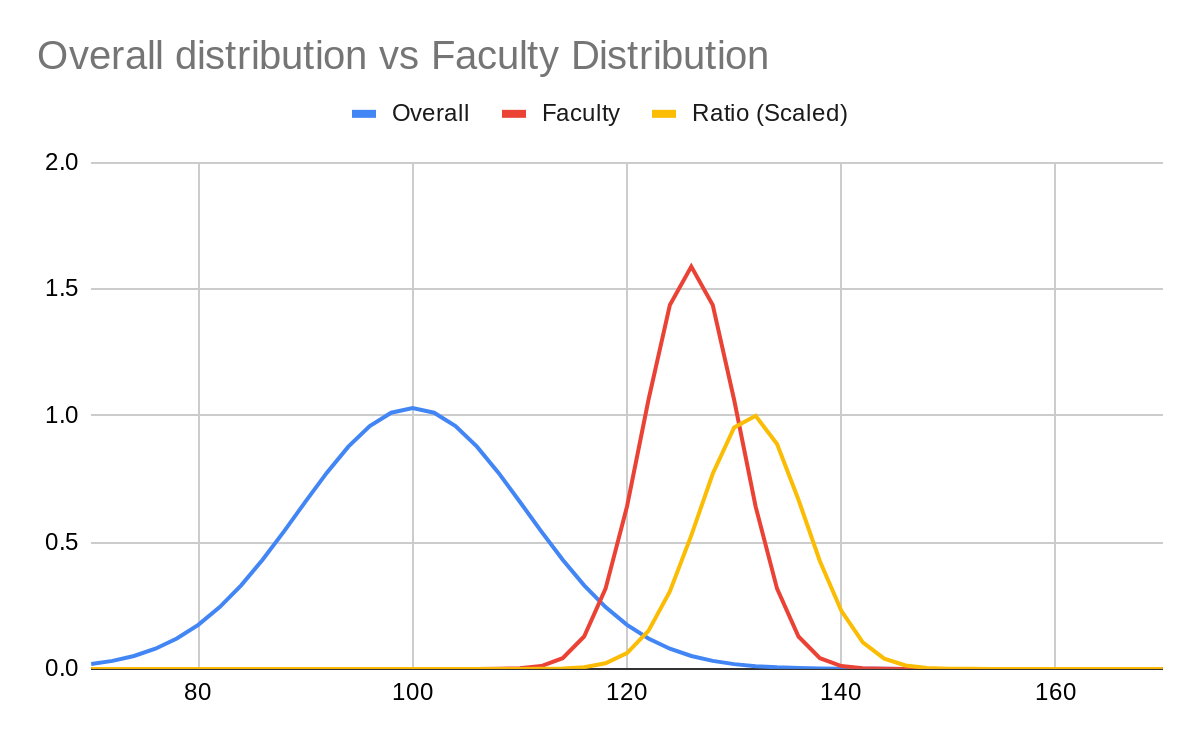
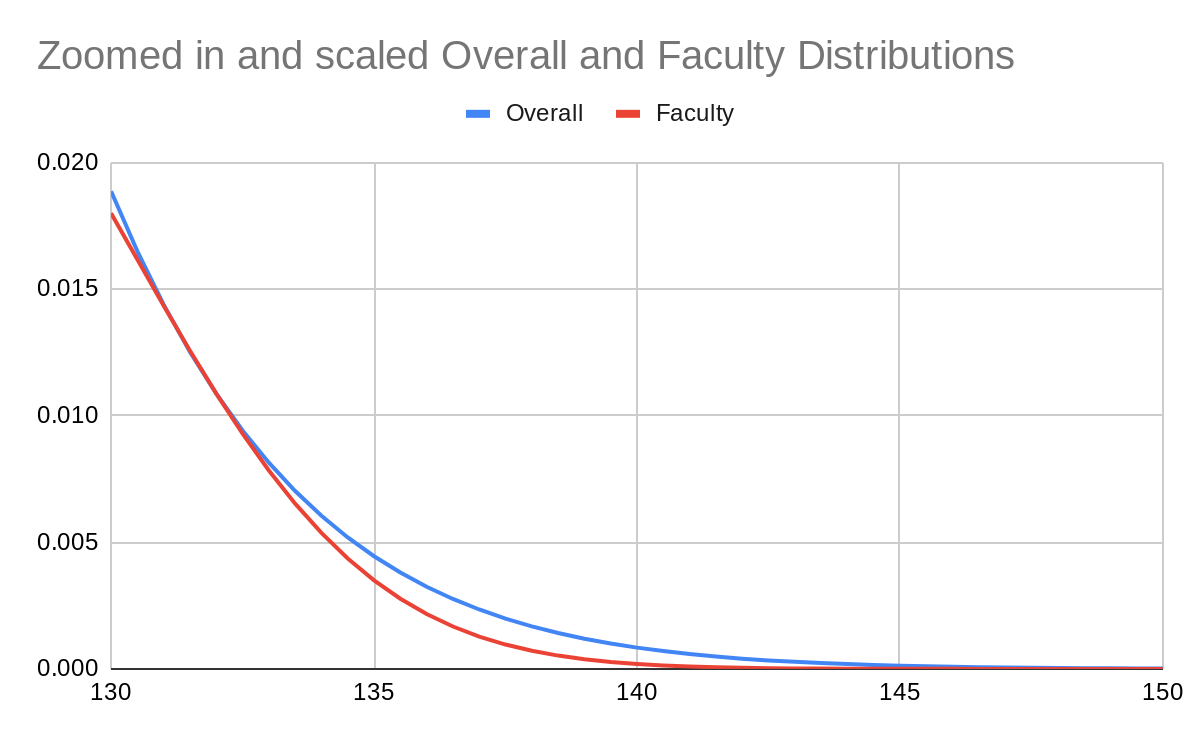
The first graph shows the distributions of the overall population (mean 100, s.d. 15) and faculty population (mean 126, s.d. 6.3) and the ratio between them (divided by ~60 so that the maximum ratio is 1 and it fits on the same graph). The ratio itself seems to peak around 133 like the article stated. So what's going on?
If we scale the two distributions so they line up between 130 and 150, we see that above around 133, the faculty distribution falls off faster. This is because of the smaller standard deviation. Normal distributions have the probability density function
for standard deviation and mean .
At values of x far from the mean, the term inside the exponential dominates the rest, and so dominates the value of the distribution, which is why the distribution of faculty drops off faster than the general population.
The mistake made in this case is assuming a normal distribution of faculty staff. Imagine a ratio function which looks like the one on the graph above, but above 133 remains constant and does not decrease. (This should match our priors on how university faculty hiring works). The distribution of faculty staff would look the same up to an iq of 133, but then would drop off slightly more slowly. This would be undetectable except by surveying an enormous number of faculty members. Normal distributions are a decent prior but they are not the only distributions which exist, especially when the distribution is created by filtering.
I don't know if this is what the authors of this particular article have done, because they won't tell us, but I suspect this is the sort of error they have made.
Yikes. If your lunatic sensor didn't go off reading this, you should get it adjusted.
From a theoretical standpoint, democratic meritocracies should evolve five IQ defined 'castes', The Leaders, The Advisors, The Followers, The Clueless and The Excluded.
If that doesn't bother you, notice that this guy is putting a lot of weight on really simplistic statistics about the edge cases (the half-percent or less of the population which is very smart and/or is "successful in" one of his preferred "intellectually elite professions"). Oh, I see Gwern actually commented about this in a comment.
Basically, this is a lovely irony of a presumed-high-IQ author jumping to a pretty ridiculous conclusion because he's not willing/able to try to dissolve his questions and do the hard work to be rigorous in his research.
If your lunatic sensor didn't go off reading this, you should get it adjusted.
A funny comment at LW.
Even lunatics can be right.
Gwern said
The assumption here is that both the general population and elite professions are described by a normal distribution (N(100,15) and N(125,6.5), respectively)
Is it? I didn't see that. assumption stated. Problem is, they didn't explicitly specify where they got their distributions. At least I don't see it.
Looking again at some of their conclusions in the preceding paragraph, it does look like they're assuming gaussians based on mean and sd a small sample, then projecting that out to the tails. Clearly malpractice.
They don't come out and say it, but the "This means that" below shows that they are extrapolating to the tails.
This means that 95% of people in intellectually elite professions have IQs between 112 and 138 99.98% have IQs between 99 and 151.
Funny that an article talking about how hard it is to be smart can be so dumb.
Still, my question remains - is there real data out there to support the contention that P(elite career|IQ) has a local max and then decreases for higher IQ?
Still, my question remains - is there real data out there to support the contention that P(elite career|IQ) has a local max and then decreases for higher IQ?
No. As I point out in my comment there, the evidence is strongly the other way: TIP/SMPY. To the extent that measures like wealth hit diminishing returns or even fall (eg Zagorsky), it has as much to do with personal choices & values as ability: the physicist who could make money on Wall Street but chooses to continue studying particles, the person who chooses to become an influential but poor writer, etc. (There are many coins of the realm, and greenbacks are but one.)
Had no idea what TIP/SMPY were.
https://en.wikipedia.org/wiki/Talent_Identification_Program
https://en.wikipedia.org/wiki/Study_of_Mathematically_Precocious_Youth
One interpretation I've seen is that ~130 is about as high as a human brain can get while still using basically the same architecture as an IQ 100 brain. The further beyond that you get, the more you're using significantly different systems. These differences may tend to be autism-related, such that the higher IQ comes at the expense of impairments.
My reading of the behavioral genetics literature is that high intelligence being driven by rare autism variants is looking unlikely. DeFries-Fulker extremes analyses like "Thinking positively: The genetics of high intelligence", Shakeshaft et al 2015 aren't consistent with the (relatively) high end being due to rare variants (but are consistent with the low end being due to rare variants) and current attempts to find rare variants enriched in the very high IQ with large effect sizes have turned up nothing: "A genome-wide analysis of putative functional and exonic variation associated with extremely high intelligence", Spain et al 2015. There is also an autism heritability observed in the GCTAs/LD score regression using only common SNPs (>=1% population frequency), along with a positive autism/intelligence genetic correlation, which undermines that idea.
My speculation at this point is that Spearman's law of diminishing returns is - based on all the genetic correlations with intelligence which have piled up and the current trends in brain imaging studies finding brain volume/thickness & global connectivity & white-matter integrity & connection speed to be the best predictors of intelligence - is due to intelligence reflecting a bottleneck between all the regions of the brain communicating to solve problems and that as the global communication becomes closer to optimal due to better health & development, individual specialized brain regions start to become the bottleneck to higher performance and shrinking the g factor.
My reading of the behavioral genetics literature is that high intelligence being driven by rare autism variants is looking unlikely.
I haven't looked at this literature, but people with autism and very high IQs might be able to fake being neurotypical. As Steve Hsu told me, we don't know if von Neumann had a normal personality because he certainly had the intelligence to fake being normal if he felt this suited his interests.
von Neumann was noted as being social and extraverted long before he began his lobbying and politicking, and was never described as a second Dirac, so I don't think he was simply acting out of expediency. If high intelligence enabled faking extraversion & social skills, which are useful in almost all contexts*, we would see a noted personality correlation with intelligence and increasing with intelligence, which we don't - extraversion is largely independent of IQ, it's Openness in the Big Five which correlates. High-functioning autistic people are also not noted for easily acquiring psychopath-level skills in imitating & manipulating without feeling.
* see for example the correlation of increasing extraversion with increasing lifetime income in the Terman semi-high IQ sample
Is anyone from LW part of a high IQ society that's more exclusive than Mensa? Can you tell us what it's like?
AFAIK, the Triple Nine Society mainly just puts out a bimonthly magazine as pdfs. Surprisingly, I couldn't find an archive of those. They have a few at their site. It was only $10 to join for a year. I joined and let it lapse. I don't have anything bad to say about it, but it obviously did not interest me enough to return, and I had forgotten about it for years since.
http://www.triplenine.org/Vidya
Wikipedia says they have a facebook group and a linked in group, but they also say two yahoo groups, and and I know yahoo canceled yahoo groups, so that page isn't up to date.
I have doubts about the definition of "elite professions". The link gives only two examples (of academia and (future) doctors) and vaguely handwaves towards "an extensive range of studies" without naming them.
One obvious observation is that capable very-high-IQ people will just do their own thing -- and will become successful e.g. businessmen or hedge fund managers or grey cardinals in politics, etc. etc.
I think they do that for the grunt level and not management positions. If the concern of the employer is that people leave the job because it's too boring it's likely not elite work.
From the comments:
Let me demonstrate how the summary statistics you report are entirely consistent with models which totally contradict your inferences.
(...)
your statistical model is bad and the data cannot support any alarmist claims about society discriminating enormously against high IQ or the need for a 'clarion call'.
There's no response to this from the author despite the passage of more than a year. Any thoughts?
I opened a question on skeptics to check the claim: http://skeptics.stackexchange.com/q/35204/196
You did read the rest of the article right, perhaps looked at the bibliography with over a dozen references?
Checkmate atheists.
(More seriously, you should've posted that to the cognitive science stack where there might actually be someone who knows something about IQ or gifted & talented education.)
It wasn't a regular user of skeptics SE but someone without any reputation on the website ;) I think questions like this are valuable to put on skeptics SE even if the question might also get an answer on cognitive science SE.
The sample consisted of mid-level leaders from multinational private-sector companies.
This sort of pre-filtered sample suffers from issues like Berkson's paradox. For example, for those managers who have IQ>120, why are they underperforming? Perhaps for lack of leadership qualities, which they make up for on intelligence. On the flip side, for managers who have unimpressive IQs (as low as <100), why are they so successful? This is why longitudinal samples like SMPY are so much more useful when you want to talk about what high IQs are or are not good for. If you run this sort of cross-sectional design, you find things like "Conscientiousness is inversely correlated with intelligence" (it's not).
This isn't really my field, and I see your point. The poster asked for other studies so I linked a study I'd recently seen. It's less about me endorsing the study than about trying to provide an entry point into the relevant literature.
WOW!! I have heard that Lesswrong.com is at the intellectual pinnacle of the Internet. Very little here is even worthy of refutation. The general population has a mean IQ of 100 and a standard deviation of 15. The elite professions have a mean IQ of 126 and a stand deviation of 6.5. If you don't believe the latter, I provided the evidence in the bibliography. Do the math. If you can't, than who cares what you think? In the article I reference the Robert Hauser work that suggests a lower mean but a higher standard deviation. If used solely, it would lower the extent of exclusion, but not by much.
The study of precocious math students shows that a talent is generally rewarded in Western society. But, if you look at the verbal scores of this group, it is clear that their quantitative SAT scores are not primarily the result of g.
Actually, this inverse correlation between very high IQ and career success is well known among top researchers. Robert Sternberg, Miraca Gross, Linda Gottfredson have all speculated on its cause. BTW, I enjoy quality criticism. However, there is none of it here.
Michael W. Ferguson
Author of the article
The article says:
The above statistics are the result of dividing the Gaussian distribution of 126 with a standard deviation of 6.7 by the IQ distribution of the total population
and I'm sorry but this is complete nonsense unless you have good evidence that (even at the tails) the "elite professions" IQ distribution is close to being Gaussian with the mean and standard deviation you cite. I bet it isn't.
To reiterate: the point is the shape of the distribution, not its mean and standard deviation. Lots of different distributions have mean 126 and standard deviation 6.5. Some of them lead to curves like the one you plotted. Some don't.
Toy model: the "elite professions" simply reject everyone with an IQ below 120 and sample at random from those with higher IQs. This gives a mean of almost exactly 127 and a standard deviation of 6.1 -- very close to the ones you quote, and if you redid your calculation with those figures you would get an even worse "exclusion" for higher IQs. But in a world matching this model, there is no real "exclusion" at all.
So, show us your evidence that the distribution of IQs in "elite professions" is close to Gaussian or, alternatively, your evidence that your analysis still works if you use a more realistic estimate of that distribution. If you can do that, then you'll have some evidence that people with very high IQ have less success in (or maybe less interest in) entering "elite professions". Otherwise, not. The argument in your actual article, as it stands, is 100% hopeless, I'm afraid.
IQ tests are designed to produce a bell curve with a mean at 100 and a standard deviation of 15. That's inherent to the definition of IQ. Actual implementations aren't perfect, but they're not far off.
Sure. But that doesn't tell us anything about the distribution of IQ among people in "elite professions", and that's the key question here.
Curated and popular this week