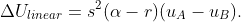On the importance of taking limits: Infinite Spheres of Utility
11VincentYu
2aspera
0VincentYu
0wedrifid
0aspera
2aspera
2VincentYu
2aspera
7MrMind
9aspera
6CronoDAS
10nshepperd
2aspera
6Kaj_Sotala
6TsviBT
2buybuydandavis
2TsviBT
1buybuydandavis
0TsviBT
3[anonymous]
2aspera
1VincentYu
0aspera
3Decius
2Pentashagon
0Decius
2aspera
5Decius
0aspera
0Decius
0aspera
2MrMind
0Decius
0MrMind
0Decius
2lmm
0Decius
0Decius
0aspera
1A1987dM
3Decius
1Manfred
0A1987dM
0Decius
0aspera
2Decius
2DanielLC
0Adele Lopez
3DanielLC
0Adele Lopez
4DanielLC
1aspera
1megasilverfist
1aspera
0D_Alex
0aspera
1buybuydandavis
0aspera
0aspera
New Comment
The answer [edited Oct 13, 2013]
As several commenters have pointed out, the original problem does not supply a method for taking limits. Our analysis shows that the problem is ill posed: it has no unique solution unless we take on additional assumptions.
I disagree that the mathematics of original problem is ill-posed, and I think DanielLC made the same point. The point of contention seems to center on the use of infinities in the original problem, which is indeed an issue if they were manipulated as real numbers, but they were not. It is perfectly acceptable and mathematical to have a countably infinite set of objects, and to define a sequence of subsets corresponding to the time evolution of that set. Infinite sets are not defined as the limit of some sequence of finite sets! There is no ambiguity in the mathematics of original problem.*
Because the use of infinity in the original problem is not in the sense of a limit, there is no good reason to think that we should take limits, or that the limits of the solutions to the finite problems should correspond in any way to the solutions of the original problem.
Where there are ambiguities are in the use of the word "utility" and similar concepts as though they were well-defined in this context. And in this sense, I agree that the original problem is ill-posed.
* There are mathematical ambiguities in an unfavorable reading of the original problem, but the following steelman removes them: Biject the people with the natural numbers, and then transfer the nth person on day n.
I added a section called "Deciding how to decide" that (hopefully) deals with this issue appropriately. I also amended the conclusion, and added you as an acknowledgement.
One of the simplest and most intuitive is aggregative utilitarianism, in which we define a utility for each person, add them all together, and make the choice with the larger total utility.
I suggest using the phrase "additive utilitarianism" rather than "aggregative utilitarianism". It was entirely my fault for saying aggregative utilitarianism in my comment, which was a misnomer; I got it mixed up with aggregative consequentialism. (All flavors of utilitarianism are by definition aggregative because they take into account the utilities from some collection of beings, but not all flavors are additive.)
Note: VincentYu has pointed out in the comments below that VNM utility may be able to deal with the infinites in this problem without taking limits.
Unfortunately, I think that ascribes too much power to VNM utility functions (that term itself is a LessWrongism; elsewhere, they would be called cardinal utility functions or just utility functions). If we had our hands on a VNM utility function, we would be okay (we simply ask it which option it prefers!), but the VNM theorem simply asserts the existence of a utility function given certain basic axioms, and it doesn't give us the utility function! So, unfortunately, VNM utility also falls flat on its face unless we already know what we prefer. (An important point is that VNM utility functions cannot work with the "utility" described in the problem. It's an unfortunate historical accident that the word "utility" is overloaded, because VNM utility requires careful handling.)
If we fail to specify the exact type of decision theory we’re using, it is entirely unclear whether taking infinite limits would lead to a self-consistent solution.
If we want to make a decision based on [additive] utility, the infinite problem is ill posed; it has no unique solution unless we take on additional assumptions.
Great, I think these are good clarifications!
Unfortunately, I think that ascribes too much power to VNM utility functions (that term itself is a LessWrongism; elsewhere, they would be called cardinal utility functions or just utility functions).
I actually don't recall seeing the usage "VNM utility functions" on less wrong at all, prior to this thread. It may have occurred previously but certainly not with sufficient frequency as to be a 'lesswrongism'. As you say, the "VNM" is unnecessary in that context since is all the VNM part does is say "it must have a utility function because it adheres to these axioms".
It is sometimes necessary to explicitly refer to things other than 'utility functions' with a 'VNM' qualifier. This is largely to pre-empt pedants who, when reading unqualified usage 'consequentialist', are not willing to assume that it refers to the only kind of consequentialist that is ever significantly discussed here (those that have utility functions).
VNM utility also falls flat on its face unless we already know what we prefer.
Not quite, but the point stands. The actual requirement is that there is any way to collect any evidence at all about our preferences (or, to be even more general, any way to cause outcomes to be correlated to our preference).
For the moment, I'm going to strike the comment from the post. I don't want to ascribe a viewpoint to VincentYu that he doesn't actually hold.
I would like to include this issue in the post, but I want to make sure I understand it first. Tell me if this is right:
It is possible mathematically to represent a countably infinite number of immortal people, as well as the process of moving them between spheres. Further, we should not expect a priori that a problem involving such infinities would have a solution equivalent to those solutions reached by taking infinite limits of an analogous finite problem. Some confusion arises when we introduce the concept of “utility” to determine which of the two choices is better, since utility only serves as a basis on which to make decision for finite problems.
If that’s what you’re saying, I have a couple of questions.
Do you view the paradox as therefore unresolvable as stated, or would you claim that a different resolution is correct?
If I carefully restricted my claim about ill-posedness to the question of which choice is better from a utilitarian sense, would you agree with it?
Tell me if this is right:
It is possible mathematically to represent a countably infinite number of immortal people, as well as the process of moving them between spheres. Further, we should not expect a priori that a problem involving such infinities would have a solution equivalent to those solutions reached by taking infinite limits of an analogous finite problem.
That's an accurate interpretation of my comment.
Some confusion arises when we introduce the concept of “utility” to determine which of the two choices is better, since utility only serves as a basis on which to make decision for finite problems.
I do think that confusion arises in this context from the concept of "utility", but not because "utility only serves as a basis on which to make decision for finite problems." The "utility" in the problem is clearly not that of VNM-utility (of which I previously gave a brief explanation) because we not assigning utility to actions, decisions, or choices (a VNM-utility function U would generally have no problem responding to an infinite set of choices, as it simply says: do argmax_{choice}(U(choice))). This severely undermines what we can do with the "utility" in the problem because we are left with the various flavors of aggregative utilitarianism, which suffer from intractable problems even in finite situations! Attempting to extend them to the situation at hand is problematic (and, as Kaj_Sotala remarked, dealing with infinities in aggregative consequentialism is the topic of one of Bostrom's papers).
- Do you view the paradox as therefore unresolvable as stated, or would you claim that a different resolution is correct?
I think that the appearance of the paradox is a consequence of unfamiliarity with infinite sets, and that it is not too surprising that our intuition appears to contradict itself in this context (by presenting each option as better than the other). The contradictory intuitions don't correspond to a logical contradiction, so the apparent paradox needs no resolution. The actual problem (choosing between the two options) is a matter of preference, just as the choice between strawberry and chocolate is a matter of preference.
2. If I carefully restricted my claim about ill-posedness to the question of which choice is better from a utilitarian sense, would you agree with it?
Absolutely. I think aggregative utilitarianism (as a moral theory) is screwed even in finite scenarios, much less infinite scenarios. (But I also think aggregative utilitarianism is a good but ill-defined general standard for comparing consequences in real life.)
Ok, I think I've got it. I'm not familiar with VNM utility, and I'll make sure to educate myself.
I'm going to edit the post to reflect this issue, but it may take me some time. It is clear (now that you point it out) that we can think of the ill-posedness coming from our insistence that the solution conform to aggregative utilitarianism, and it may be possible to sidestep the paradox if we choose another paradigm of decision theory. Still, I think it's worth working as an example, because, as you say, AU is a good general standard, and many readers will be familiar with it. At the minimum, this would be an interesting finite AU decision problem.
Thanks for all the time you've put into this.
The plots were done in Mathematica 9, and then I added the annotations in PowerPoint, including the dashed lines. I had to combine two color functions for the density plot, since I wanted to highlight the fact that the line s=n represented indifference. Here's the code:
r = 1; ua = 1;ub = -1; f1[n, s] := (ns - s^2r ) (ua - ub); Show[DensityPlot[-f1[n, s], {n, 0, 20}, {s, 0, 20}, ColorFunction -> "CherryTones", Frame -> False, PlotRange -> {-1000, 0}], DensityPlot[f1[n, s], {n, 0, 20}, {s, 0, 20}, ColorFunction -> "BeachColors", Frame -> False, PlotRange -> {-1000, 0}]]
The Ross-Littlewood Paradox is amusing.
You have an infinite collection of balls in a storeroom, labeled with the natural numbers (1, 2, 3, etc.) and a vase that can hold any number, or all, of them.
At each integer time T, starting with T=1, you take the 10 lowest numbered balls out of the storeroom and put them in the vase, and then take the lowest numbered ball out of the vase and destroy it. So at any finite time T, there are 9T balls in the vase and all the balls labeled with a number less than or equal to T have been destroyed.
Now, because the number of balls at any given time T is given by 9T, in the limit as T approaches infinity, there are infinitely many balls in the vase. On the other hand, because every ball has a time T at which it will be destroyed, the limit of the set of balls in the vase as T approaches infinity is the empty set. So at T = infinity, you have an empty vase that contains infinitely many balls.
The moral of the story is to be careful what limits you take, because taking two different limits can give two different answers even if they seem like they're measuring the same thing.
(Can this be used as an argument for the existence of nonstandard numbers?)
This is actually a good example of the difference between pointwise and uniform convergence. Consider the characteristic function of the vase at time t, g_t : N -> {0, 1}. Then g_t(n) = 1 if and only if ball n is in the vase at time t. It will actually help to convert g_t to a function on the real numbers, by making f_t(x) = g_t(floor(x)).
Now, for each ball n, there is a time when it will be destroyed, and therefore will never be in the vase after that time. So the characteristic function f_t(x) converges pointwise to f(x) = 0. This is presumably what you mean by the limit of the vase being the empty set.
But the criterion of uniform convergence is that for any epsilon>0 there is a t such that f_t is within epsilon of the limit everywhere. Which is obviously not true, because at any time t there are some balls in the vase, and so the characteristic function is 1 somewhere. So f_t(x) does not uniformly converge to anything.
As it happens, without uniform convergence, the limit of the integrals of f_t(x) (which just so happens to be the number of balls in the vase, by my setup) is not generally equal to the integral of the limiting function f(x). So, in a way it is not really true that you can say
in the limit as T approaches infinity, there are infinitely many balls in the vase
as the integral does not transfer to the limit.
Great problem, thanks for mentioning it!
I think the answer to "how many balls did you put in the vase as T->\infty" and "How many balls have been destroyed as T->\infty" both have well defined answers. It's just a fallacy to assume that the "total number of balls in the vase as T->\infty" is equal to the difference between these quantities in their limits.
On the difficulties that infinities pose to utilitarianism, see also Nick Bostrom's Infinite Ethics.
Two of the best fundamental probability guys, Jaynes and Wolpert, both basically said that the applications of their theories to infinite sets were unnecessary and likely more trouble than they're worth.
Yeah I read PT:LOS and I'd like to be able to say that, but infinite ethics doesn't really look to be so easily swept under the rug.
Would you recommend The Mathematics of Generalization by Wolpert, and/or something else?
Amazon doesn't provide an index, but the title was promising enough that I bought one. The date looks good too, as it was after I know much of the original papers were completed.
What you want are his general framework for analyzing generalization problems, and his application of that framework to Stacked Generalization and No Free Lunch Theorems in machine learning and Search/Optimization.
Sorry I don't have better details, but the papers are in storage, and I read them 15+ years ago.
Nice.
Bug reports:
Note that even though t is 1, we'll end up with a unit error if we don't carry it around.
I think you meant r here.
And you have flipped the sign of \Delta U_{linear}.
Does it matter if the number of people is countably infinite, or uncountably infinite?
If each person corresponds on a 1-1 basis with the real numbers, there are an infinite number people who will not be selected to change spheres on any of the integer-numbered days. Those people will never change spheres.
Just compare the cardinality of the number of days to the cardinality of the number of people. If |days| < |people| then start them in the heaven sphere. If |days| = |people| then it doesn't matter (by symmetry the first are last, and the last first, so to speak). If |days| > |people| then start them in the hell sphere.
My first impression was the same as yours, but then I realized there was no guarantee about any of the cardinality, even for the set of days. The post assumes the reals, but comparing the cardinality should work for any sets (although if they're bigger than the reals can we really compare "utility" at all?)
In the above example, the number of people and the number of days they live were uncountable, if I'm not mistaken. The take-home message is that you do not get an answer if you just evaluate the problem for sets like that, but you might if you take a limit.
Conclusions that involve infinity don't map uniquely on to finite solutions because they don't supply enough information. Above, "infinite immortal people" refers to a concept that encapsulates three different answers. We had to invent a new parameter, alpha, which was not supplied in the original problem, to come up with a well defined result. In essence, we didn't actually answer the question. We made up our own problem that was similar to the original one.
Provided you can assign a unique rational number to each day each person lives, they are countable.
I will note that the expected time for a given person to remain in the sphere in which they started is infinite, provided they don't know in what order they will be removed. The summation for each day becomes (total of an infinite number of people)+(total of a finite number of people); if we assume that a person-day in bliss is positive and a person-day in agony is negative, then the answer is trivial. An infinite summation of terms of positive infinity is greater than an infinite sum of terms of negative infinity- the cardinalities are irrelevant.
Thanks for clearing up the countability. It's clear that there are some cases where taking limits will fail (like when the utility is discontinuous at infinity), but I don't have an intuition about how that issue is related to countability.
You said 'discontinuous at infinity'. Did you mean 'the infinite limit diverges or otherwise does not exist'?
No, I mean a function whose limit doesn't equal its defined value at infinity. As a trivial example, I could define a utility function to be 1 for all real numbers in [-inf,+inf) and 0 for +inf. The function could never actually be evaluated at infinity, so I'm not sure what it would mean, but I couldn't claim that the limit was giving me the "correct" answer.
The function could never actually be evaluated at infinity, so I'm not sure what it would mean, but I couldn't claim that the limit was giving me the "correct" answer.
If you accept the Axiom of Infinity, there's no problem at evaluating a function at infinity. The problem is rather that omega is a regular limit cardinal, so there's no way to define the value at infinity from the value at the successor, unless you include in the definition an explicit step for limit cardinals.
You can very well define a function that has 1 as value on 0 and on every successor cardinal, but 0 on every limit cardinal. The function will indeed be discontinuous, but its value at omega will be perfectly defined (I just did).
The problem with saying a function is not continuous at infinity is that the definitions of 'continuous' requires the standard definition of 'limit' (sigma-epsilon), while the definition of limits at infinity uses the same nomenclature and similar notation, but expresses something different.
Consider the case where F(X-epsilon) is 1, F(X) is 0, and F(X+epsilon) is either 0 or undefined. The common thought there is that the limit at X does not exist; why is that any different just because X is infinite, without sacrificing the concept which allows us to talk about continuity in terms of limits?
The problem with saying a function is not continuous at infinity is that the definitions of 'continuous' requires the standard definition of 'limit' (sigma-epsilon), while the definition of limits at infinity uses the same nomenclature and similar notation, but expresses something different.
Well... I guess you can see it that way if you want, but in set theory (again, everything I say is under the axiom of infinity) both notions are unified under the notion of limit in the order topology.
In this way, you can define a continuous function for every transfinite ordinal.
Consider the case where F(X-epsilon) is 1, F(X) is 0, and F(X+epsilon) is either 0 or undefined. The common thought there is that the limit at X does not exist; why is that any different just because X is infinite, without sacrificing the concept which allows us to talk about continuity in terms of limits?
Yes, I understand that the concept of limit in calculus and set theory means something a little different. Possibly this is just arguing over definitions: in calculus, it is said that a limit doesn't exist when the function has a different value w.r.t. the value calculated using the topology of its domain, but in set theory a limit is defined in a different way, using only the order topology. In this sense, a function can be defined at omega, at omega+1, omega+2, etc. After all, that's the raison d'etre of the entire concept. Under this assumption, you just say that if the function is defined at omega, and if it has a different value at omega than the one defined from its order topology, you just say that it's discontinuous.
Let me clarify with an example: the function y = 2x, defined in set theory, would have at omega the limit omega (demonstration below). If you just define a similar function but that has at omega the value 0, then you have a discontinuous function, because the (topological) limit is different from the defined value.
Of course, if you want, you can just say that the (simple) limit doesn't exists when this situation arise, I was on the other side pointing to the fact that a function can be perfectly defined and continuous or discontinuous at infinity.
Thesis
Omega is the limit of y=2x, defined on the natural number.
Demonstration
The intersection of the range of the function with omega is still the range of the function.
The range is unbounded but every one of its member is finite: since omega is regular limit, it is never reached by the sequence. So, any ordinal greater then or equal to omega is an upper bound. But omega is also an initial ordinal, so is the least upper bound.
That is, the least upper bound of the intersection of the range of the function with omega is still omega, so by definition omega is the limit of the range of the function. QED.
TIL that mathematicians commonly strictly define terms in one context, then extend them into other contexts in ways that are not strictly compatible with the original context.
Now I understand that two people with significantly different levels of math education and understanding lack the common vocabulary required to trivially communicate basic math-related concepts.
It's still going to be hard to convince me that the sum of an infinite number of days, each of which has infinite positive utility and finite negative utility, will ever be lower than zero.
It's still going to be hard to convince me that the sum of an infinite number of days, each of which has infinite positive utility and finite negative utility, will ever be lower than zero.
Remember you're not allowed to talk about infinity except as a limit.
Consider the sequence:
1. 1 person, 3 days - utility 1 - 1 - 1 = -1
2. 2 people, 6 days - utility 2 + 0 - 2 - 2 - 2 - 2 = -6
3. 3 people, 9 days - utility 3 + 1 - 1 - 3 - 3 - 3 - 3 - 3 - 3 = -15
4. 4 people, 12 days - utility 4 + 2 + 0 - 2 - 4 - 4 - 4 - 4 - 4 - 4 - 4 - 4 = -28
etc.
Clearly the limit of this sequence is the sum you're talking about (that is, the utility of an infinite number of immortal people who start in sphere A, where we move one each day to sphere B). At the same time, clearly the limit of this sequence is negative.
(Of course the "real" answer is that it's not well defined; there are many sequences we can construct that come out as "infinite immortal people" in the limit, and the utility is different depending which we pick. But this is an example of why "lower than zero" is as legitimate an answer as "higher than zero").
Except that in the original problem, there cannot be more days than people;
...each day, one more person gets permanently transferred across to...
(Emphasis added.)
Then again, rephrasing the problem in equivalent ways has interesting effects:
Assume that the number of people is countable; assign each of them a natural number, but don't tell them which one it is.
Suppose that on the Nth day you move the person with the Nth prime number to the opposite sphere; every individual prefers case 1, where they have 100% chance of infinite happiness.
Suppose that you tell everyone their number and on the Nth day you move the person with the Nth number to the opposite sphere; every individual prefers case 2, where they have a finite period of agony followed by infinite happiness.
What's the Erdos number of an infinite number of monkeys juggling an infinite number of bananas?
Um... -inf and +inf are not real numbers. (Noting that your function as described is undefined at -inf.)
In addition, the definition of continuous restricts it to points which exist on an open interval; if the limit from below and limit from above are equal to the value at X, then the function is continuous on an open interval containing X. How do you determine the limit as X approaches +inf from above?
That can also happen if there are countably infinite people. Suppose that for each n, on the n-th day the 2n-th person is moved from hell to heaven. All the odd-numbered people will stay in hell forever.
Conclusions that involve infinity cannot generally be generalized to any finite solution; this seems like a 'each monkey now has two bananas' moment.
The finite analogue come from the fact that infinity minus infinity is undefined, and can be anything from "still infinity" (like if you had infinity people and then only sent away the even numbered ones) to any number you choose, to negative infinity. In a finite problem, the answer becomes well-defined, but there are multiple possible answers.
Consider the converse: Is there a way to arrange the days and people such that it is better to start in hell? Trivially, it seems like the simple solution is that way, since each person leaves hell after a finite number of days and then spends infinity days in heaven, but I lack the concept which allows me to find the amount of time the average person spends in hell.
My problem with this is how do you know the proper way to take the limit? The scenario isn't a limit. It's just something with infinities in it. The limit is something we force onto it.
Another, finite, problem occurred to me:
Suppose there are two bliss spheres, that are equally good. You can either spend one year in sphere A or one year in sphere B.
If you spend 1-1/n years in sphere A vs. one year in sphere B, sphere B is always better. The limit of these cases is the original problem, so sphere B must be better. Similarly, sphere A must be better.
Perhaps if you can get two answers from two different limits, that just means that they're the same. The problem is that it's really easy to get this to happen. Just use something similar to Pascal's wager. This would mean that everything is the same, which is a completely useless utility function.
My problem with this is how do you know the proper way to take the limit? The scenario isn't a limit. It's just something with infinities in it. The limit is something we force onto it.
And as such, it is ambiguous. The limit is how we resolve the ambiguity.
If you take a particular converging limit, that gives you a resolution to the ambiguity, but the idea of taking a limit does not. You're just picking your answer when you pick your limit.
Deciding what to do in situations involving infinities by invoking limits is not a well-defined decision theory.
Deciding what to do in situations involving infinities by invoking limits is not a well-defined decision theory.
Well yes, because those situations are not well-defined without some additional structure capturing something which also describes the limiting process.
There is no additional structure. It's not as if we can come upon two pairs of spheres, and notice while the end result is the same, they're the limits of two different processes, and therefore different choices are better. There is only the infinite case. If you want to consider sequence that converge to it, there's no clear way to decide which sequence to look at.
Limits help you if you're looking at an extreme value. If the limit as the population goes to infinity is that a random sample of X of them will give you Y confidence on a poll, then you can just use that if there's a large population. If you're dealing with the limit itself, it doesn't always help. You can start with a square, and then cut little squares off of the corners, and then more squares off of those corners etc. until you approach a circle. The perimeter will always be four times the length, but this won't be true of the circle.
In this problem, you can get literally any answer if you take the limit appropriately, so once you've decided on the right answer, there is some way to get to it with the limit, but deciding that the right answer is one that a limit converges to helps you not at all.
The problem isn't a sequence of finite cases. It's just the infinite case all by itself.
You're completely right! As stated, the problem is ill posed, i.e. it has no unique solution, so we didn't solve it.
Instead, we solved a similar problem by introducing a new parameter, \alpha. It was useful because we gained a mathematical description that works for very large n and s, and which matches our intuition about the problem.
It is important to recognize, as you point out, that that taking limits does not solve the problem. It just elucidates why we can't solve it as stated.
Given that the original problem involves discrete units (one person once a day) is it correct to treat infinity as being a cluster point/limit point of the function
Thanks to whomever moved this to Discussion. From the FAQ, I wasn't sure where to put it. This is better, in retrospect.
I'm not sure why it got moved: maybe not central to the thesis of LW, or maybe not high enough quality. I'm going to add some discussion of counter-arguments to the limit method. Maybe that will make a difference.
I noticed that the discussion picked up when it got moved, and I learned some useful stuff from it, so I'm not complaining.
Very nice work.
I feel it accomplishes too much for most people, though, so that they might not get everything out of it.
Great as a demonstration of Jaynes' point about paradoxes generate by failure to identify the limiting process for proposed infinities. But also great as a demonstration of how "doing the math" can resolve a lot of these philosophical debates which just don't specify problem conditions sufficiently because they don't explicitly write them down in mathematical form.
I think a lot of the self referential problems many like around here (Omega stuff, as an example) would be similarly dissolved by the latter.
I agree that it's a lot to cover, but I wanted to work a full example. We talk a lot on LW about decision analysis and paradoxes in the abstract, but I'm coming from a math/physics background, and it's much more helpful for me to see concrete examples. I assume some other people feel the same way.
Self-referential problems would be an interesting area to study, but I'm not familiar with the techniques. I suspect you're right, though.