I haven't read this in detail but one very quick comment: Cox's Theorem is a representation theorem showing that coherent belief states yield classical probabilities, it's not the same as the dutch-book theorem at all. E.g. if you want to represent probabilities using log odds, they can certain relate to each other coherently (since they're just transforms of classical probabilities), but Cox's Theorem will give you the classical probabilities right back out again. Jaynes cites a special case of Cox in PT:TLOS which is constructive at the price of assuming probabilities are twice differentiable, and I actually tried it with log odds and got the classical probabilities right back out - I remember being pretty impressed with that, and had this enlightenment experience wherein I went to seeing probability theory as a kind of relational structure in uncertainty.
I also quickly note that the worst-case scenario often amounts to making unfair assumptions about "randomization" wherein adversaries can always read the code of deterministic agents but non-deterministic agents have access to hidden sources of random numbers. E.g. http://lesswrong.com/lw/vq/the_weighted_majority_algorithm/
Good catch on Cox's theorem; that is now fixed. Do you know if the dutch book argument corresponds to a named theorem?
I'm not sure exactly how your comment about deterministic vs. non-deterministic agents is meant to apply to the arguments I've advanced here (although I suppose you will clarify after you're done reading).
Separately, I disagree that the assumptions are unfair; I think of it as a particularly crisp abstraction of the actual situation you care about. As long as pseudo-random generators exist and you can hide your source of randomness, you can guarantee that no adversary can predict your random bits; if you could usefully make the same guarantee about other aspects of your actions without recourse to a PRG then I would happily incorporate that into the set of assumptions, but in practice it is easiest to just work in terms of a private source of randomness. Besides, I think that the use of this formalism has been amply validated by its intellectual fruits (see the cited network flow application as one example, or the Arora, Hazan, and Kale reference).
Good catch on Cox's theorem; that is now fixed. Do you know if the dutch book argument corresponds to a named theorem?
There is a whole class of dutch book arguments, so I'm not sure which one you mean by the dutch book argument.
In any case, Susan Vineberg's formulation of the Dutch Book Theorem goes like this:
Given a set of betting quotients that fails to satisfy the probability axioms, there is a set of bets with those quotients that guarantees a net loss to one side.
Then you might think you could have inconsistent betting prices that would harm the person you bet with, but not you, which sounds fine.
Rather: "If your betting prices don't obey the laws of probability theory, then you will either accept combinations of bets that are sure losses, or pass up combinations of bets that are sure gains."
Well, Cox's Theorem still assumes that you're representing belief-strengths with real numbers in the first place. Really you should go back to Savage's Theorem... :)
I've tried to do something similar with odds once, but the assumption about (AB|C) = F[(A|C), (B|AC)] made me give up.
Indeed, one can calculate O(AB|C) given O(A|C) and O(B|AC) but the formula isn't pretty. I've tried to derive that function but failed. It was not until I appealed to the fact that O(A)=P(A)/(1-P(A)) that I managed to infer this unnatural equation about O(AB|C), O(A|C) and O(B|AC).
And this use of classical probabilities, of course, completely defeats the point of getting classical probabilities from the odds via Cox's Theorem!
Did I miss something?
By the way, are there some other interesting natural rules of inference besides odds and log odds which are isomorphic to the rules of probability theory? (Judea Pearl mentioned something about MYCIN certainty factor, but I was unable to find any details)
EDIT: You can view the CF combination rules here, but I find it very difficult to digest. Also, what about initial assignment of certainty?
EDIT2: Nevermind, I found an adequate summary ( http://www.idi.ntnu.no/~ksys/NOTES/CF-model.html ) of the model and pdf ( http://uai.sis.pitt.edu/papers/85/p9-heckerman.pdf ) about probabilistic interpretations of CF. It seems to be an interesting example of not-obviously-Bayesian system of inference, but it's not exactly an example you would give to illustrate the point of Cox's theorem.
When the assumptions of Bayes' Theorem hold, and when Bayesian updating can be performed computationally efficiently, then it is indeed tautological that Bayes is the optimal approach. Even when some of these assumptions fail, Bayes can still be a fruitful approach. However, by working under weaker (sometimes even adversarial) assumptions, frequentist approaches can perform well in very complicated domains even with fairly simple models; this is because, with fewer assumptions being made at the outset, less work has to be done to ensure that those assumptions are met.
I've only skimmed this for now (will read soon), but I wanted to point out that I completely agree with this conclusion (without reading the arguments in detail). However, I might frame it differently: both Bayesian statistics and frequentist statistics are useful only insofar as they approximate the true Bayesian epistemology. In other words, if you know the prior and know the likelihood, then performing the Bayesian update will give P(A|data) where A is any question you're interested in. However, since we usually don't know our prior or likelihood, there's no guarantee that Bayesian statistics -- which amounts to doing the Bayesian update on the wrong model of the actual structure of our uncertainty (i.e. our actual prior + likelihood) -- will closely approximate Bayesian epistemology. So, of course we should consider other methods that, while superficially don't look like the true Bayesian update, may do a better job of approximating the answer we want. Computational difficulty is a separate reason why we might have to approximate Bayesian epistemology even if we can write down the prior + likelihood and that, once again, might entail using methods that don't look "Bayesian" in any way.
If you recall, I briefly made this argument to you at the July minicamp, but you didn't seem to find it persuasive. I'll note now that I'm simply not talking about decision theory. So, e.g., when you say
It follows, then, that Bayes is the superior method whenever we can obtain a good prior and when good average-case performance is sufficient.
I'm not taking a position on whether we need to consider whether we need average-case performance to be sufficient in order for using Bayesian statistics to be the best or a good option (I have intuitions going both directions, but nothing fleshed out).
I predict that you'll probably answer my question in the later essay since my position hinges, crucially, one whether Bayesian epistemology is correct, but do you see anything that you disagree with here?
I predict that you'll probably answer my question in the later essay since my position hinges, crucially, one whether Bayesian epistemology is correct, but do you see anything that you disagree with here?
Nope, everything you said looks good! I actually like the interpretation you gave:
However, I might frame it differently: both Bayesian statistics and frequentist statistics are useful only insofar as they approximate the true Bayesian epistemology.
I don't actually intend to take a position on whether Bayesian epistemology is correct; I merely plan to talk about implications and relationships between different interpretations of probability and let people decide for themselves which to prefer, if any. Although if I had to take a position, it would be something like, "Bayes is more correct than frequentist but frequentist ideas can provide insight into patching some of the holes in Bayesian epistemology". For instance, I think UDT is a very frequentist thing to do.
A nice middle-ground between purely Bayesian and purely frequentist methods is to use a Bayesian model coupled with frequentist model-checking techniques; this gives us the freedom in modeling afforded by a prior but also gives us some degree of confidence that our model is correct. This approach is suggested by both Gelman [9] and Jordan [10].
Just to pile on a little bit here: A Bayesian might argue that uncertainty about which model you're using is just uncertainty, so put a prior on the space of possible models and do the Bayesian update. This can be an effective method, but it doesn't entirely get rid of the problem - now you're modeling the structure of your uncertainty about models in a particular way, and that higher level model could be wrong. You're also probably excluding some plausible possible models, but I'll sidestep that issue for now. The Bayesian might argue that this case is analogous to the previous - just model your (model of the structure of uncertainty about models) - put a prior on that space too. But eventually this must stop with a finite number of levels of uncertainty, and there's no guarantee that 1) your model is anywhere near the true model (i.e. the actual structure of your uncertainty) or 2) you'll be able to get answers out of the mess you've created.
On the other hand, frequentist model checking techniques can give you a pretty solid idea of how well the model is capturing the data. If one model doesn't seem to be working, try another instead! Now a Bayesian might complain that this is "using the data twice" which isn't justified by probability theory, and they would be right. However, you don't get points for acting like a Bayesian, you get points for giving the same answer as a Bayesian. What the Bayesian in this example should be worried about is whether the model chosen at the end ultimately gives answers that are close to what a true Bayesian would give. Intuitively, I think this is the case - if a model doesn't seem to fit the data by some frequentist model checking method, e.g. a goodness of fit test, then it's likely that if you could actually write down the posterior probability that the particular model you chose is true (i.e. it's the true structure of your uncertainty), that probability would be small, modulo a high degree of prior certainty that the model was true. But I'm willing to be proven wrong on this.
As Andrew Critch [6] insightfully points out, the Bayesians vs. frequentists debate is really three debates at once, centering around one or more of the following arguments:...
I think there's a much more important and fundamental debate you're missing in your taxonomy, and one of the wellsprings of LW criticism: the sub-category of frequentist techniques called null hypothesis testing. There are legitimate & powerful frequentist criticisms of NHST, and these are accepted and echoed as major arguments by many who are otherwise on an opposite side for one of those other debates.
For my part, I'm sure that NHST is badly misleading and wrong, but I'm not so sure that I can tar all the other frequentist techniques with the same brush.
Bayesian methods make stronger assumptions than may be warranted, and frequentists methods provide little in the way of a coherent framework for constructing models, and ask for worst-case guarantees, which probably cannot be obtained in general.
As a non-expert in the area, I find that this implies that "Bayesian methods" are unsuitable for FAI research, as preventing UFAI requires worst-case guarantees coupled with the assumption that AI can read your source code. This must be wrong, otherwise EY would not trumpet Bayesianism so much. What did I miss?
If I apply Frequentist Decision Theory As Described By Jsteinhardt (FDTADBJ) to a real-world decision problem, where θ ranges over all possible worlds (as opposed to a standard science paper where θ ranges over only a few parameters of some restricted model space), then the worst case isn't "we need to avoid UFAI", it's "UFAI wins and there's nothing we can do about it". Since there is at least one possible world where all actions have an expected utility of "rocks fall, everyone dies", that's the only possible world that affects worst case utility. So FDTADBJ says there's no point in even trying to optimize for the case where it's possible to survive.
Yup, exactly. It seems possible to me that you can get around this within the frequentist framework, but most likely it's the case that you need to at least use Bayesian ideas somewhere to get an AI to work at all.
I plan to write up a sketch of a possible FAI architecture based on some of the ideas paulfchristiano has been developing; hopefully that will clarify some of these points.
For those who really want to discuss interpretations of probability, I will address that in a later essay.
I am still waiting with bated breath. :-)
Sorry about that! I'm really behind on writing right now, and probably will be for at least the next month as I work on a submission to NIPS (http://nips.cc/). I have a few other writing things to catch up on before this, but still hope to get to it eventually.
These theorems, however, ignore the issue of computation --- while the best decision procedure may be Bayesian, the best computationally-efficient decision procedure could easily be non-Bayesian.
This raises another important point against Bayes, which is that the proper Bayesian interpretation may be very mathematically complex.
if we are trying to build a software package that should be widely deployable, we might want to use a frequentist method because users can be sure that the software will work as long as some number of easily-checkable assumptions are met.
I think these are the strongest reasons you've raised that we might want to deviate from pure Bayesianism in practice. We usually think of these (computation and understandability-by-humans) as irritating side issues, to be glossed over and mostly considered after we've made our decision about which algorithm to use. But in practice they often dominate all other considerations, so it would be nice to find a way to rigorously integrate these two desiderata with the others that underpin Bayesianism.
In fact, now that the year is 2012 the majority of new graduate students are being raised as Bayesians (at least in the U.S.) with frequentists thought of as stodgy emeritus professors stuck in their ways.
Is this actually true? Where would one get numbers on such a thing?
No, it's not true. This whole F vs B thing is such a false choice too. Does it make sense in computational complexity to have a holy war between average case and worst case analysis of algorithm running time? Maybe for people who go on holy wars as a hobby, but not as a serious thing.
I don't understand why this was linked as a response at all. Randomization is conjectured not to help in the sense that people think P = BPP. But there are cases where randomization does strictly help (wikipedia has a partial list: http://en.wikipedia.org/wiki/Randomized_algorithm).
My point was about sociology. Complexity theorists are not bashing each other's heads in over whether worst case or average case analysis is "better," they are proving theorems relating the approaches, with the understanding that in some algorithm analysis applications, it makes sense to take the "adversary view," for example in real time systems that need strict guarantees. In other applications, typical running time is a more useful quantity. Nobody calls worst case analysis an apostate technique. Maybe that's a good example to follow. Keep religion out of math, please.
Keep religion out of math, please.
I agree with this. That was supposed to be the point of the post.
Randomization is conjectured not to help in the sense that people think P = BPP.
Even if P = BPP, randomization still probably helps; P = BPP just means that randomization doesn't help so much that it separates polynomial from non-polynomial.
Your analogy is imprecise. Average case and worst case analyses are both useful in their own right, and deal with different phenomena; F and B claim to deal with the same phenomena, but F is usually more vague about what assumptions its techniques follow from.
A more apt analogy, in my opinion, would be between interpretations of QM. All of them claim to deal with the same phenomena, but some interpretations are more vague about the precise mechanism than others.
Why do you think F is more vague than B? I don't think that's true. LW folks (up to and including EY) are generally a lot more vague and imprecise when talking about statistics than professional statisticians using F for whatever reason. But still seem to have strong opinions about B over F. It's kinda culty, to be honest.
Here's a book by a smart F:
http://www.amazon.com/All-Statistics-Statistical-Inference-Springer/dp/0387402721
The section on B stat is fairly funny.
F techniques tend to make assumptions that are equivalent to establishing prior distributions, but because it's easy to forget about these assumptions, many people use F techniques without considering what the assumptions mean. If you are explicit about establishing priors, however, this mostly evaporates.
Notice that the point about your analogy was regarding area of application, not relative vagueness.
I don't have a strong personal opinion about F/B. This is just based on informal observations about F techniques versus B techniques.
many people use F techniques without considering what the assumptions mean
Can you name three examples of this happening?
Every biology paper released based on a 5% P-value threshold without regard to the underlying plausibility of the connection. There are many effects where I wouldn't take a 0.1% P-value to mean anything (see: kerfluffle over superluminal neutrinos), and some where I'd take a 10% P-value as a weak but notable degree of confirmation.
I could, but I doubt anything would come of it. Forget about the off-hand vagueness remark; the analogy still fails.
"Area of app" depends on granularity: "analysis of running time" (e.g. "how long will this take, I haven't got all day") is an area of app, but if we are willing to drill in we can talk about distributions on input vs worst case as separate areas of app. I don't really see a qualitative difference here: sometimes F is more appropriate, sometimes not. It really depends on how much we know about the problem and how paranoid we are being. Just as with algorithms -- sometimes input distributions are reasonable, sometimes not.
Or if we are being theoretical statisticians, our intended target for techniques we are developing. I am not sympathetic to "but the unwashed masses don't really understand, therefore" kind of arguments. Math techniques don't care, it's best to use what's appropriate.
edit: in fact, let the utility function u(.) be the running time of an algorithm A, and the prior over theta the input distribution for algorithm A inputs. Now consider what the expectation for F vs the expectation for B is computing. This is a degenerate statistical problem, of course, but this isn't even an analogy, it's an isomorphism.
The section on B stat is fairly funny.
No doubt about it, Larry Wasserman* is a smart guy. Unfortunately, that section isn't his finest work. The normal prior example compares apples and oranges as discussed here, and the normalizing constant paradox analysis is just wrong, as LW himself discusses here.
* I'm just a teeny bit jealous that his initials are "LW". How awesome would that be?
Data point: One of our Montreal LW meetup members showed us a picture and description pulled from his Bayes stats/analysis class, and the picture shows kiosks with the hippy bayes person and the straight-suited old-and-set-in-his-ways corporate clone, along with the general idea that frequentist thinking is good for long-term verification and reliability tests, but that people who promote frequentism over bayes when both are just as good are Doing Something Wrong (AKA sneer at the other tribe).
I don't think anyone needs anecdotes that Bayesian approaches are more popular than ever before or are a bona fide approach; I'm interested in the precise claim that now a majority of grad students identify as Bayesians. That is the interest.
I don't have precise numbers but this is my experience after having worked with ML groups at Cambridge, MIT, and Stanford. The next most common thing after Bayesians would be neural nets people if I had to guess (I don't know what you want to label those as). Note that as a Bayesian-leaning person I may have a biased sample.
I suspect Berkeley might be more frequentist but am unsure.
Another answer is the complete class theorem, which shows that any non-Bayesian decision procedure is strictly dominated by a Bayesian decision procedure --- meaning that the Bayesian procedure performs at least as well as the non-Bayesian procedure in all cases with certainty.
I don't understand the connection to the earlier claims about minimizing worst-case performance. To strictly dominate, doesn't this imply that the Bayesian algorithm does as well or better on the worst-case input? In which case, how does frequentism ever differ? Surely the complete class theorem doesn't show that all frequentist approaches are just a Bayesian approah in disguise?
I don't understand why Bayesians are presented as going for expected value while Frequentists are going for worst-case. These seem kind of orthogonal issues.
Support vector machines [2], which try to pick separating hyperplanes that minimize generalization error, are one example of this where the algorithm is explicitly trying to maximize worst-case utility.
Could you expand on this a little? I've always thought of SVMs as minimizing an expected loss (the sum over hinge losses) rather than any best-worst-case approach. Are you referring to the "max min" in the dual QP? I'm interested in other interpretations...
Finally, Bayes has no good way of dealing with […] with cases where the data was generated in a complicated way that could make it highly biased […].
Wait, what? If we don't know about the possibility of bias, we're doomed anyway, are we not? If we do know about it, then we just have to adjust our prior, right? Or is this again about the intractability of true Bayesian computation in complicated cases?
Some random thoughts:
In order to fix "Bayesian Decision Theory" so that it works in multiplayer games, have it search through strategies for the one that leads to maximum utility, rather than just going action by action. I guess this may be a non-mainstream thing?
Bayes is the superior method whenever we can obtain a good prior and when good average-case performance is sufficient. However, if we have no way of obtaining a good prior, or when we need guaranteed performance, frequentist methods are the way to go.
If you "need guaranteed performance," just include that information in the utility function.
the Bayesians vs. frequentists debate is really three debates at once, centering around one or more of the following arguments:
Whether to interpret subjective beliefs as probabilities
Whether to interpret probabilities as subjective beliefs (as opposed to asymptotic frequencies)
Whether a Bayesian or frequentist algorithm is better suited to solving a particular problem.Why are these arguments so commonly conflated?
Given the rest of your article, it looks like "conflated" could be replaced by "correlated" here. Calling the relationship between ideals and algorithms "conflation" already judges the issue a bit :)
In order to fix "Bayesian Decision Theory" so that it works in multiplayer games, have it search through strategies for the one that leads to maximum utility, rather than just going action by action. I guess this may be a non-mainstream thing?
Nope, that's definitely a standard thing to do. It's what I was referring to when I said:
We can incorporate notions like planning and value of information by defining U(θ; a) recursively in terms of an identical agent to ourselves who has seen one additional observation (or, if we are planning against an adversary, in terms of the adversary).
However, this doesn't actually work that well, since recursively modeling other agents is expensive, and if the adversary is more complicated than our model can capture, we will do poorly. It is often much better to just not assume that we have a model of the adversary in the first place.
If you "need guaranteed performance," just include that information in the utility function.
There is a difference between "guaranteed performance" and "optimizing for the worst case". Guaranteed performance means that we can be confident, before the algorithm gets run, that it will hit some performance threshold. I don't see how you can do that with a Bayesian method, except by performing a frequentist analysis on it.
Given the rest of your article, it looks like "conflated" could be replaced by "correlated" here. Calling the relationship between ideals and algorithms "conflation" already judges the issue a bit :)
When terminology fails to carve reality at its joints then I think it is fair to refer to it as conflation. If it was indeed the case that ideals mapped one-to-one onto algorithms then I would reconsider my word choice.
There is a difference between "guaranteed performance" and "optimizing for the worst case". Guaranteed performance means that we can be confident, before the algorithm gets run, that it will hit some performance threshold.
Ah, okay. Whoops.
I don't see how you can do that with a Bayesian method, except by performing a frequentist analysis on it.
How about a deliberate approximation to an ideal use of the evidence? Or do any approximations with limited ranges of validity (i.e. all approximations) count as "frequentist"? Though then we might have to divide computer-programming frequentists into "bayesian frequentists" and "frequentist frequentists" depending on whether they made approximations or applied a toolbox of methods.
How about a deliberate approximation to an ideal use of the evidence?
I'm confused by what you are suggesting here. Even a Bayesian method making no approximations at all doesn't necessarily have guaranteed performance (see my response to Oscar_Cunningham).
I'm referring to using an approximation in order to guarantee performance. E.g. replacing the sum of a bunch of independent, well-behaved random variables with a gaussian, and using monte-carlo methods to get approximate properties of the individual random variables with known resources if necessary.
There is a difference between "guaranteed performance" and "optimizing for the worst case".
I'm not sure what the difference between these two is, could you spell it out for me?
"Guaranteed performance" typically cashes out as "replace the value of an action with the probability that its outcome is better than L, then pick the best" whereas "optimizing for the worst case" typically cashes out as "replace the value of an action with the value of its worst outcome, then pick the best."
The latter is often referred to as "robustness" and the former as "partial robustness," and which one is applicable depends on the situation. Generally, the latter is used in problems with severe probabilistic uncertainty, whereas the former needs some probabilistic certainty.
Suppose that there are two possible policies A and B, and in the worst case A gives utility 1 and B gives utility 2, but for the specific problem we care about we require a utility of 3. Then an algorithm that optimizes for the worst case will choose B. On the other hand, there is no algorithm (that only chooses between policies A and B) that can guarantee a utility of 3. If you absolutely need a utility of 3 then you'd better come up with a new policy C, or find an additional valid assumption that you can make. The subtlety here is that "optimizing for the worst case" implicitly means "with respect to the current set of assumptions I have encoded into my algorithm, which is probably a subset of the full set of assumptions that I as a human make about the world".
The notion of guaranteed performance is important because it tells you when you need to do more work and design a better algorithm (for instance, by finding additional regularities of the environment that you can exploit).
(Note: this is cross-posted from my blog and also available in pdf here.)
If you are a newly initiated student into the field of machine learning, it won't be long before you start hearing the words "Bayesian" and "frequentist" thrown around. Many people around you probably have strong opinions on which is the "right" way to do statistics, and within a year you've probably developed your own strong opinions (which are suspiciously similar to those of the people around you, despite there being a much greater variance of opinion between different labs). In fact, now that the year is 2012 the majority of new graduate students are being raised as Bayesians (at least in the U.S.) with frequentists thought of as stodgy emeritus professors stuck in their ways.
If you are like me, the preceding set of facts will make you very uneasy. They will make you uneasy because simple pattern-matching -- the strength of people's opinions, the reliability with which these opinions split along age boundaries and lab boundaries, and the ridicule that each side levels at the other camp – makes the "Bayesians vs. frequentists" debate look far more like politics than like scholarly discourse. Of course, that alone does not necessarily prove anything; these disconcerting similarities could just be coincidences that I happened to cherry-pick.
My next point, then, is that we are right to be uneasy, because such debate makes us less likely to evaluate the strengths and weaknesses of both approaches in good faith. This essay is a push against that --- I summarize the justifications for Bayesian methods and where they fall short, show how frequentist approaches can fill in some of their shortcomings, and then present my personal (though probably woefully under-informed) guidelines for choosing which type of approach to use.
Before doing any of this, though, a bit of background is in order...
1. Background on Bayesians and Frequentists
1.1. Three Levels of Argument
As Andrew Critch [6] insightfully points out, the Bayesians vs. frequentists debate is really three debates at once, centering around one or more of the following arguments:
Given my own research interests, I will add a fourth argument:
4. Whether Bayesian or frequentist techniques are better suited to engineering an artificial intelligence.
Andrew Gelman [9] has his own well-written essay on the subject, where he expands on these distinctions and presents his own more nuanced view.
Why are these arguments so commonly conflated? I'm not entirely sure; I would guess it is for historical reasons but I have so far been unable to find said historical reasons. Whatever the reasons, what this boils down to in the present day is that people often form opinions on 1. and 2., which then influence their answers to 3. and 4. This is not good, since 1. and 2. are philosophical in nature and difficult to resolve correctly, whereas 3. and 4. are often much easier to resolve and extremely important to resolve correctly in practice. Let me re-iterate: the Bayes vs. frequentist discussion should center on the practical employment of the two methods, or, if epistemology must be discussed, it should be clearly separated from the day-to-day practical decisions. Aside from the difficulties with correctly deciding epistemology, the relationship between generic epistemology and specific practices in cutting-edge statistical research is only via a long causal chain, and it should be completely unsurprising if Bayesian epistemology leads to the employment of frequentist tools or vice versa.
For this reason and for reasons of space, I will spend the remainder of the essay focusing on statistical algorithms rather than on interpretations of probability. For those who really want to discuss interpretations of probability, I will address that in a later essay.
1.2. Recap of Bayesian Decision Theory
(What follows will be review for many.) In Bayesian decision theory, we assume that there is some underlying world state θ and a likelihood function p(X1,...,Xn | θ) over possible observations. (A likelihood function is just a conditional probability distribution where the parameter conditioned on can vary.) We also have a space A of possible actions and a utility function U(θ; a) that gives the utility of performing action a if the underlying world state is θ. We can incorporate notions like planning and value of information by defining U(θ; a) recursively in terms of an identical agent to ourselves who has seen one additional observation (or, if we are planning against an adversary, in terms of the adversary). For a more detailed overview of this material, see the tutorial by North [11].
What distinguishes the Bayesian approach in particular is one additional assumption, a prior distribution p(θ) over possible world states. To make a decision with respect to a given prior, we compute the posterior distribution pposterior(θ | X1,...,Xn) using Bayes' theorem, then take the action a that maximizes]) .
.
In practice, pposterior(θ | X1,...,Xn) can be quite difficult to compute, and so we often attempt to approximate it. Such attempts are known as approximate inference algorithms.
1.3. Steel-manning Frequentists
There are many different ideas that fall under the broad umbrella of frequentist techniques. While it would be impossible to adequately summarize all of them even if I attempted to, there are three in particular that I would like to describe, and which I will call frequentist decision theory, frequentist guarantees, and frequentist analysis tools.
Frequentist decision theory has a very similar setup to Bayesian decision theory, with a few key differences. These are discussed in detail and contrasted with Bayesian decision theory in [10], although we summarize the differences here. There is still a likelihood function p(X1,...,Xn | θ) and a utility function U(θ; a). However, we do not assume the existence of a prior on θ, and instead choose the decision rule a(X1,...,Xn) that maximizes
In other words, we ask for a worst case guarantee rather than an average case guarantee. As an example of how these would differ, imagine a scenario where we have no data to observe, an unknown θ in {1,...,N}, and we choose an action a in {0,...,N}. Furthermore, U(0; θ) = 0 for all θ, U(a; θ) = -1 if a = θ, and U(a;θ) = 1 if a ≠ 0 and a ≠ θ. Then a frequentist will always choose a = 0 because any other action gets -1 utility in the worst case; a Bayesian, on the other hand, will happily choose any non-zero value of a since such an action gains (N-2)/N utility in expectation. (I am purposely ignoring more complex ideas like mixed strategies for the purpose of illustration.).
Note that the frequentist optimization problem is more complicated than in the Bayesian case, since the value of (1) depends on the joint behavior of a(X1,...,Xn), whereas with Bayes we can optimize a(X1,...,Xn) for each set of observations separately.
As a result of this more complex optimization problem, it is often not actually possible to maximize (1), so many frequentist techniques instead develop tools to lower-bound (1) for a given decision procedure, and then try to construct a decision procedure that is reasonably close to the optimum. Support vector machines [2], which try to pick separating hyperplanes that minimize generalization error, are one example of this where the algorithm is explicitly trying to maximize worst-case utility. Another example of a frequentist decision procedure is L1-regularized least squares for sparse recovery [3], where the procedure itself does not look like it is explicitly maximizing any utility function, but a separate analysis shows that it is close to the optimal procedure anyways.
The second sort of frequentist approach to statistics is what I call a frequentist guarantee. A frequentist guarantee on an algorithm is a guarantee that, with high probability with respect to how the data was generated, the output of the algorithm will satisfy a given property. The most familiar example of this is any algorithm that generates a frequentist confidence interval: to generate a 95% frequentist confidence interval for a parameter θ is to run an algorithm that outputs an interval, such that with probability at least 95% θ lies within the interval. An important fact about most such algorithms is that the size of the interval only grows logarithmically with the amount of confidence we require, so getting a 99.9999% confidence interval is only slightly harder than getting a 95% confidence interval (and we should probably be asking for the former whenever possible).
If we use such algorithms to test hypotheses or to test discrete properties of θ, then we can obtain algorithms that take in probabilistically generated data and produce an output that with high probability depends only on how the data was generated, not on the specific random samples that were given. For instance, we can create an algorithm that takes in samples from two distributions, and is guaranteed to output 1 whenever they are the same, 0 whenever they differ by at least ε in total variational distance, and could have arbitrary output if they are different but the total variational distance is less than ε. This is an amazing property --- it takes in random input and produces an essentially deterministic answer.
Finally, a third type of frequentist approach seeks to construct analysis tools for understanding the behavior of random variables. Metric entropy, the Chernoff and Azuma-Hoeffding bounds [12], and Doob's optional stopping theorem are representative examples of this sort of approach. Arguably, everyone with the time to spare should master these techniques, since being able to analyze random variables is important no matter what approach to statistics you take. Indeed, frequentist analysis tools have no conflict at all with Bayesian methods --- they simply provide techniques for understanding the behavior of the Bayesian model.
2. Bayes vs. Other Methods
2.1. Justification for Bayes
We presented Bayesian decision theory above, but are there any reasons why we should actually use it? One commonly-given reason is that Bayesian statistics is merely the application of Bayes' Theorem, which, being a theorem, describes the only correct way to update beliefs in response to new evidence; anything else can only be justified to the extent that it provides a good approximation to Bayesian updating. This may be true, but Bayes' Theorem only applies if we already have a prior, and if we accept probability as the correct framework for expressing uncertain beliefs. We might want to avoid one or both of these assumptions. Bayes' theorem also doesn't explain why we care about expected utility as opposed to some other statistic of the distribution over utilities (although note that frequentist decision theory also tries to maximize expected utility).
One compelling answer to this is dutch-booking, which shows that any agent must implicitly be using a probability model to make decisions, or else there is a series of bets that they would be willing to make that causes them to lose money with certainty. Another answer is the complete class theorem, which shows that any non-Bayesian decision procedure is strictly dominated by a Bayesian decision procedure --- meaning that the Bayesian procedure performs at least as well as the non-Bayesian procedure in all cases with certainty. In other words, if you are doing anything non-Bayesian, then either it is secretly a Bayesian procedure or there is another procedure that does strictly better than it. Finally, the VNM Utility Theorem states that any agent with consistent preferences over distributions of outcomes must be implicitly maximizing the expected value of some scalar-valued function, which we can then use as our choice of utility function U. These theorems, however, ignore the issue of computation --- while the best decision procedure may be Bayesian, the best computationally-efficient decision procedure could easily be non-Bayesian.
Another justification for Bayes is that, in contrast to ad hoc frequentist techniques, it actually provides a general theory for constructing statistical algorithms, as well as for incorporating side information such as expert knowledge. Indeed, when trying to model complex and highly structured situations it is difficult to obtain any sort of frequentist guarantees (although analysis tools can still often be applied to gain intuition about parts of the model). A prior lets us write down the sorts of models that would allow us to capture structured situations (for instance, when trying to do language modeling or transfer learning). Non-Bayesian methods exist for these situations, but they are often ad hoc and in many cases ends up looking like an approximation to Bayes. One example of this is Kneser-Ney smoothing for n-gram models, an ad hoc algorithm that ended up being very similar to an approximate inference algorithm for the hierarchical Pitman-Yor process [15, 14, 17, 8]. This raises another important point against Bayes, which is that the proper Bayesian interpretation may be very mathematically complex. Pitman-Yor processes are on the cutting-edge of Bayesian nonparametric statistics, which is itself one of the more technical subfields of statistical machine learning, so it was probably much easier to come up with Kneser-Ney smoothing than to find the interpretation in terms of Pitman-Yor processes.
2.2. When the Justifications Fail
The first and most common objection to Bayes is that a Bayesian method is only as good as its prior. While for simple models the performance of Bayes is relatively independent of the prior, such models can only capture data where frequentist techniques would also perform very well. For more complex (especially nonparametric) Bayesian models, the performance can depend strongly on the prior, and designing good priors is still an open problem. As one example I point to my own research on hierarchical nonparametric models, where the most straightforward attempts to build a hierarchical model lead to severe pathologies [13].
Even if a Bayesian model does have a good prior, it may be computationally intractable to perform posterior inference. For instance, structure learning in Bayesian networks is NP-hard [4], as is topic inference in the popular latent Dirichlet allocation model (and this continues to hold even if we only want to perform approximate inference). Similar stories probably hold for other common models, although a theoretical survey has yet to be made; suffice to say that in practice approximate inference remains a difficult and unsolved problem, with many models not even considered because of the apparent hopelessness of performing inference in them.
Because frequentist methods often come with an analysis of the specific algorithm being employed, they can sometimes overcome these computational issues. One example of this mentioned already is L1 regularized least squares [3]. The problem setup is that we have a linear regression task Ax = b+v where A and b are known, v is a noise vector, and x is believed to be sparse (typically x has many more rows than b, so without the sparsity assumption x would be underdetermined). Let us suppose that x has n rows and k non-zero rows --- then the number of possible sparsity patterns is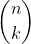 --- large enough that a brute force consideration of all possible sparsity patterns is intractable. However, we can show that solving a certain semidefinite program will with high probability yield the appropriate sparsity pattern, after which recovering x reduces to a simple least squares problem. (A semidefinite program is a certain type of optimization problem that can be solved efficiently [16].)
--- large enough that a brute force consideration of all possible sparsity patterns is intractable. However, we can show that solving a certain semidefinite program will with high probability yield the appropriate sparsity pattern, after which recovering x reduces to a simple least squares problem. (A semidefinite program is a certain type of optimization problem that can be solved efficiently [16].)
Finally, Bayes has no good way of dealing with adversaries or with cases where the data was generated in a complicated way that could make it highly biased (for instance, as the output of an optimization procedure). A toy example of an adversary would be playing rock-paper-scissors --- how should a Bayesian play such a game? The straightforward answer is to build up a model of the opponent based on their plays so far, and then to make the play that maximizes the expected score (probability of winning minus probability of losing). However, such a strategy fares poorly against any opponent with access to the model being used, as they can then just run the model themselves to predict the Bayesian's plays in advance, thereby winning every single time. In contrast, there is a frequentist strategy called the multiplicative weights update method that fairs well against an arbitrary opponent (even one with superior computational resources and access to our agent's source code). The multiplicative weights method does far more than winning at rock-paper-scissors --- it is also a key component of the fastest algorithm for solving many important optimization problems (including the network flow algorithm), and it forms the theoretical basis for the widely used AdaBoost algorithm [1, 5, 7].
2.3. When To Use Each Method
The essential difference between Bayesian and frequentist decision theory is that Bayes makes the additional assumption of a prior over θ, and optimizes for average-case performance rather than worst-case performance. It follows, then, that Bayes is the superior method whenever we can obtain a good prior and when good average-case performance is sufficient. However, if we have no way of obtaining a good prior, or when we need guaranteed performance, frequentist methods are the way to go. For instance, if we are trying to build a software package that should be widely deployable, we might want to use a frequentist method because users can be sure that the software will work as long as some number of easily-checkable assumptions are met.
A nice middle-ground between purely Bayesian and purely frequentist methods is to use a Bayesian model coupled with frequentist model-checking techniques; this gives us the freedom in modeling afforded by a prior but also gives us some degree of confidence that our model is correct. This approach is suggested by both Gelman [9] and Jordan [10].
3. Conclusion
When the assumptions of Bayes' Theorem hold, and when Bayesian updating can be performed computationally efficiently, then it is indeed tautological that Bayes is the optimal approach. Even when some of these assumptions fail, Bayes can still be a fruitful approach. However, by working under weaker (sometimes even adversarial) assumptions, frequentist approaches can perform well in very complicated domains even with fairly simple models; this is because, with fewer assumptions being made at the outset, less work has to be done to ensure that those assumptions are met.
From a research perspective, we should be far from satisfied with either approach --- Bayesian methods make stronger assumptions than may be warranted, and frequentists methods provide little in the way of a coherent framework for constructing models, and ask for worst-case guarantees, which probably cannot be obtained in general. We should seek to develop a statistical modeling framework that, unlike Bayes, can deal with unknown priors, adversaries, and limited computational resources.
4. Acknowledgements
Thanks to Emma Pierson, Vladimir Slepnev, and Wei Dai for reading preliminary versions of this work and providing many helpful comments.
5. References
[1] Sanjeev Arora, Elad Hazan, and Satyen Kale. The multiplicative weights update method: a meta algorithm and applications. Working Paper, 2005.
[2] Christopher J.C. Burges. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 2:121--167, 1998.
[3] Emmanuel J. Candes. Compressive sampling. In Proceedings of the International Congress of Mathematicians. European Mathematical Society, 2006.
[4] D.M. Chickering. Learning bayesian networks is NP-complete. LECTURE NOTES IN STATISTICS-NEW YORK-SPRINGER VERLAG-, pages 121--130, 1996.
[5] Paul Christiano, Jonathan A. Kelner, Aleksander Madry, Daniel Spielman, and Shang-Hua Teng. Electrical flows, laplacian systems, and faster approximation of maximum flow in undirected graphs. In Proceedings of the 43rd ACM Symposium on Theory of Computing, 2011.
[6] Andrew Critch. Frequentist vs. bayesian breakdown: Interpretation vs. inference. http://lesswrong.com/lw/7ck/frequentist_vs_bayesian_breakdown_interpretation/.
[7] Yoav Freund and Robert E. Schapire. A short introduction to boosting. Journal of Japanese Society for Artificial Intelligence, 14(5):771--780, Sep. 1999.
[8] J. Gasthaus and Y.W. Teh. Improvements to the sequence memoizer. In Advances in Neural Information Processing Systems, 2011.
[9] Andrew Gelman. Induction and deduction in bayesian data analysis. RMM, 2:67--78, 2011.
[10] Michael I. Jordan. Are you a bayesian or a frequentist? Machine Learning Summer School 2009 (video lecture at http://videolectures.net/mlss09uk_jordan_bfway/).
[11] D. Warner North. A tutorial introduction to decision theory. IEEE Transactions on Systems Science and Cybernetics, SSC-4(3):200--210, Sep. 1968.
[12] Igal Sason. On refined versions of the Azuma-Hoeffding inequality with applications in information theory. CoRR, abs/1111.1977, 2011.
[13] Jacob Steinhardt and Zoubin Ghahramani. Pathological properties of deep bayesian hierarchies. In NIPS Workshop on Bayesian Nonparametrics, 2011. Extended Abstract.
[14] Y.W. Teh. A bayesian interpretation of interpolated Kneser-Ney. Technical Report TRA2/06, School of Computing, NUS, 2006.
[15] Y.W. Teh. A hierarchical bayesian language model based on pitman-yor processes. Coling/ACL, 2006.
[16] Lieven Vandenberghe and Stephen Boyd. Semidefinite programming. SIAM Review, 38(1):49--95, Mar. 1996.
[17] F.~Wood, C.~Archambeau, J.~Gasthaus, L.~James, and Y.W. Teh. A stochastic memoizer for sequence data. In Proceedings of the 26th International Conference on Machine Learning, pages 1129--1136, 2009.