LESSWRONG
LW

Comment Permalink
Vaniver40

First, thanks for your patience.

Conclusion: I don't agree with Harsanyi's claim that the linear combination of utility functions is unique up to linear transformations. I agree it is unique up to affine transformations, and the discrepancy between my statement and his is explained by his comment "on the understanding that the zero point of the social welfare function is appropriately chosen." (Why he didn't explicitly generalize to affine transformations is beyond me.)

I don't think the claim "the utility function can be expressed as a linear combination of the individual utility functions" is particularly meaningful, because it just means that the aggregated utility function must exist in the space spanned by the individual utility functions. I'd restate it as:

If the aggregator introduces new values not shared by humans, it is willing to trade human values to get them, and thus is not a friendly aggregator.

(Because, as per VNM, all values are comparable.) Also, note that this might not be a necessary condition for friendliness, but it is a necessary condition for axiom 2-ness.

Notes:

I've been representing the utilities as vectors, and it seems like moving to linear algebra will make this discussion much cleaner.

Suppose the utility vector for an individual is a row vector. We can combine their preferences into a matrix P=[A;B;C].

In order to make a counterexample, we need a row vector S which 1) is linearly independent of P, that is, rank[P;S] =/= rank[P]. Note that if P has rank equal to the number of outcomes, this is impossible; all utility functions can be expressed as linear combinations. In our particular example, the rank of P is 3, and there are 4 outcomes, so S=null[P]=[-1,0,0,0], and we can confirm that rank[P;S]=4. (Note that for this numerical example, S is equivalent to a affinely transformed C, but I'm not sure if this is general.)

We also need S to 2) satisfy any preferences shared by all members of P. We can see gambles as column vectors, with each element being the probability that a gamble leads to a particular outcome; all values should be positive and sum to one. We can compare gambles by subtracting them; A*x-A*y gives us the amount that A prefers x to y. Following Harsanyi, we'll make it share indifferences; that is, if A*(x-y)=0, then A is indifferent between x and y, and if P*(x-y) is a zero column vector, then all members of the population are indifferent.

Let z=(x-y), and note that P*z=0 is the null space of P, which we used earlier to identify a candidate S, because we knew incorporating one of the vectors of the null space would increase the rank. We need S*z=0 for it to be indifferent when P is indifferent; this requires that the null space of P have at least two dimensions. (So three independent agents aggregated in four dimensions isn't enough!)

We also need the sum of z to be zero for it to count as a comparison between gambles, which is equivalent to [1,1,1,1,1]*z=0. If we get lucky, this occurs normally, but we're not guaranteed two different gambles that all members of the population are indifferent between. If we have a null space of at least three dimensions, then that is guaranteed to happen, because we can toss the ones vector in as another row to ensure that all the vectors returned by null sum to 0.

So, if the null space of P is at least 2-dimensional, we can construct a social welfare function that shares indifferences, and if the null space of P is at least 3-dimensional, those indifferences are guaranteed to exist. But sharing preferences is a bit tougher- we need every case where P*z>0 to result in S*z>0. Since z=x-y, we have the constraint that the sum of z's elements must add up to 0, which makes things weirder, since it means we need to consider at least two elements at once.

So it's not clear to me yet that it's impossible to construct S which shares preferences and is linearly independent, but I also haven't generated a constructive method to do so in general.

Reply
AlexMennen50

I don't agree with Harsanyi's claim that the linear combination of utility functions is unique up to linear transformations. I agree it is unique up to affine transformations, and the discrepancy between my statement and his is explained by his comment "on the understanding that the zero point of the social welfare function is appropriately chosen." (Why he didn't explicitly generalize to affine transformations is beyond me.)

I'm not quite sure what you mean. Are you talking about the fact that you can add a constant to utility function without... (read more)

Reply
See in context
by AlexMennen
AI Alignment Forum
4 min read
90

37

Ω 7

A Friendly AI would have to be able to aggregate each person's preferences into one utility function. The most straightforward and obvious way to do this is to agree on some way to normalize each individual's utility function, and then add them up. But many people don't like this, usually for reasons involving utility monsters. If you are one of these people, then you better learn to like it, because according to Harsanyi's Social Aggregation Theorem, any alternative can result in the supposedly Friendly AI making a choice that is bad for every member of the population. More formally,

Axiom 1: Every person, and the FAI, are VNM-rational agents.

Axiom 2: Given any two choices A and B such that every person prefers A over B, then the FAI prefers A over B.

Axiom 3: There exist two choices A and B such that every person prefers A over B.

(Edit: Note that I'm assuming a fixed population with fixed preferences. This still seems reasonable, because we wouldn't want the FAI to be dynamically inconsistent, so it would have to draw its values from a fixed population, such as the people alive now. Alternatively, even if you want the FAI to aggregate the preferences of a changing population, the theorem still applies, but this comes with it's own problems, such as giving people (possibly including the FAI) incentives to create, destroy, and modify other people to make the aggregated utility function more favorable to them.)

Give each person a unique integer label from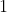 to , where is the number of people. For each person 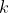, let 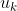be some function that, interpreted as a utility function, accurately describes 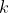's preferences (there exists such a function by the VNM utility theorem). Note that I want 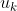to be some particular function, distinct from, for instance, 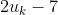, even though 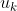and 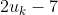represent the same utility function. This is so it makes sense to add them.

Theorem: The FAI maximizes the expected value of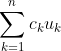 , for some set of scalars .

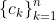Actually, I changed the axioms a little bit. Harsanyi originally used “Given any two choices A and B such that every person is indifferent between A and B, the FAI is indifferent between A and B” in place of my axioms 2 and 3 (also he didn't call it an FAI, of course). For the proof (from Harsanyi's axioms), see section III of Harsanyi (1955), or section 2 of Hammond (1992). Hammond claims that his proof is simpler, but he uses jargon that scared me, and I found Harsanyi's proof to be fairly straightforward.

Harsanyi's axioms seem fairly reasonable to me, but I can imagine someone objecting, “But if no one else cares, what's wrong with the FAI having a preference anyway. It's not like that would harm us.” I will concede that there is no harm in allowing the FAI to have a weak preference one way or another, but if the FAI has a strong preference, that being the only thing that is reflected in the utility function, and if axiom 3 is true, then axiom 2 is violated.

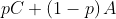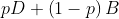proof that my axioms imply Harsanyi's: Let A and B be any two choices such that every person is indifferent between A and B. By axiom 3, there exists choices C and D such that every person prefers C over D. Now consider the lotteries and , for 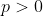. Notice that every person prefers the first lottery to the second, so by axiom 2, the FAI prefers the first lottery. This remains true for arbitrarily small 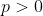, so by continuity, the FAI must not prefer the second lottery for 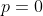; that is, the FAI must not prefer B over A. We can “sweeten the pot” in favor of B the same way, so by the same reasoning, the FAI must not prefer A over B.

So why should you accept my axioms?

Axiom 1: The VNM utility axioms are widely agreed to be necessary for any rational agent.

Axiom 2: There's something a little rediculous about claiming that every member of a group prefers A to B, but that the group in aggregate does not prefer A to B.

Axiom 3: This axiom is just to establish that it is even possible to aggregate the utility functions in a way that violates axiom 2. So essentially, the theorem is “If it is possible for anything to go horribly wrong, and the FAI does not maximize a linear combination of the people's utility functions, then something will go horribly wrong.” Also, axiom 3 will almost always be true, because it is true when the utility functions are linearly independent, and almost all finite sets of functions are linearly independent. There are terrorists who hate your freedom, but even they care at least a little bit about something other than the opposite of what you care about.

At this point, you might be protesting, “But what about equality? That's definitely a good thing, right? I want something in the FAI's utility function that accounts for equality.” Equality is a good thing, but only because we are risk averse, and risk aversion is already accounted for in the individual utility functions. People often talk about equality being valuable even after accounting for risk aversion, but as Harsanyi's theorem shows, if you do add an extra term in the FAI's utility function to account for equality, then you risk designing an FAI that makes a choice that humanity unanimously disagrees with. Is this extra equality term so important to you that you would be willing to accept that?

Remember that VNM utility has a precise decision-theoretic meaning. Twice as much utility does not correspond to your intuitions about what “twice as much goodness” means. Your intuitions about the best way to distribute goodness to people will not necessarily be good ways to distribute utility. The axioms I used were extremely rudimentary, whereas the intuition that generated "there should be a term for equality or something" is untrustworthy. If they come into conflict, you can't keep all of them. I don't see any way to justify giving up axioms 1 or 2, and axiom 3 will likely remain true whether you want it to or not, so you should probably give up whatever else you wanted to add to the FAI's utility function.

Citations:

Harsanyi, John C. "Cardinal welfare, individualistic ethics, and interpersonal comparisons of utility." The Journal of Political Economy (1955): 309-321.

Hammond, Peter J. "Harsanyi’s utilitarian theorem: A simpler proof and some ethical connotations." IN R. SELTEN (ED.) RATIONAL INTERACTION: ESSAYS IN HONOR OF JOHN HARSANYI. 1992.

Coherent Extrapolated VolitionUtility Functions
Personal Blog

37

Ω 7

Mentioned in
Harsanyi's Social Aggregation Theorem and what it means for CEV
New Comment
90 comments, sorted by
top scoring
Click to highlight new comments since:
Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings
[-]Qiaochu_Yuan340

So when you're talking about decision theory and your intuitions come into conflict with the math, listen to the math.

I think you're overselling your case a little here. The cool thing about theorems is that their conclusions follow from their premises. If you then try to apply the theorem to the real world and someone dislikes the conclusion, the appropriate response isn't "well it's math, so you can't do that," it's "tell me which of my premises you dislike."

An additional issue here is premises which are not explicitly stated. For example, there's an implicit premise in your post of there being some fixed collection of agents with some fixed collection of preferences that you want to aggregate. Not pointing out this premise explicitly leaves your implied social policy potentially vulnerable to various attacks involving creating agents, destroying agents, or modifying agents, as I've pointed out in other comments.

Reply
[-]Wei Dai120

I suggest the VNM Expected Utility Theorem and this theorem should be used as a test on potential FAI researchers. Is their reaction to these theorems "of course, the FAI has to be designed that way" or "that's a cool piece of math, now let's see if we can't break it somehow"? Maybe you don't need everyone on the research team to instinctively have the latter reaction, but I think you definitely want to make sure at least some do. (I wonder what von Neumann's reaction was to his own theorem...)

Reply
8AlexMennen
That's a good point. I agree, and I've edited my post to reflect that. I thought I was being explicit about that when I was writing it, but looking at my post again, I now see that I was not. I've edited it to try to clarify that. Thanks for pointing those out.
[-]Kaj_Sotala90

Axiom 1: Every person, and the FAI, are VNM-rational agents.

[...]

So why should you accept my axioms?

Axiom 1: The VNM utility axioms are widely agreed to be necessary for any rational agent.

Though of course, humans are not VNM-rational.

Reply
2AlexMennen
Only a VNM-rational agent can have preferences in a coherent way, so if we're talking about aggregating people's preferences, I don't see any way to do it other than modeling people as having underlying VNM-rational preferences that fail to perfectly determine their decisions.
6Academian
Non-VNM agents satisfying only axiom 1 have coherent preferences... they just don't mix well with probabilities.
2steven0461
Presumably there would be first be an extrapolation phase resulting in rational preferences.
[-]615C68A690

There's something a little rediculous about claiming that every member of a group prefers A to B, but that the group in aggregate does not prefer A to B.

That would look a bit like Simpson's paradox actually.

Reply
7Oscar_Cunningham
The situation analogous to Simpson's paradox can only occur if for some reason we care about some people's opinion more than others in some situations (this is analogous to the situation in Simpson's paradox where we have more data points in some parts of the table than others. It is a necessary condition for the paradox to occur.) For example: Suppose Alice (female) values a cure for prostate cancer at 10 utils, and a cure for breast cancer at 15 utils. Bob (male) values a cure for prostate cancer at 100 utils, and a cure for breast cancer at 150 utils. Suppose that because prostate cancer largely affects men and breast cancer largely affects women we value Alice's opinion twice as much about breast cancer and Bob's opinion twice as much about prostate cancer. Then in the aggregate curing prostate cancer is 210 utils and curing breast cancer 180 utils, a preference reversal compared to either of Alice or Bob.
3AlexMennen
This is essentially just an example of Harsanyi's Theorem in action. And I think it makes a compelling demonstration of why you should not program an AI in that fashion.
0615C68A6
Isn't that the description of an utility maximizer (or optimizer) taking into account the preferences of an utility monster?
0Oscar_Cunningham
To get the effect that we need an optimiser that cares about some people's opinion more about some things but then for some other things cares about someone else's opinion. If we just have a utility monster who the optimiser always values more than others we can't get the effect. The important thing is that it sometimes cares about one person and sometimes cares about someone else.
2Luke_A_Somers
I don't see how it's like Simpson's paradox, actually. You want to go to Good Hospital instead of Bad Hospital even if more patients who go to Good Hospital die because they get almost the hard cases. Aggregating only hides the information needed to make a properly informed choice. Here, aggregating doesn't hide any information. But there are a bunch of other ways things like that can happen. This very morning I did a nonlinear curvefit on a bunch of repeats of an experiment. One of the parameters that came out had values in the range -1 to +1. I combined the data sets directly and that parameter for the combined set came out around 5. In a way, this analogy may be even more directly applicable than Simpson's paradox. Even if A and B are complete specifications (unlike that parameter, which was one of several), the interpersonal reactions to other people can do some very nonlinear things to interpretations of A and B.
[-]buybuydandavis80

But many people don't like this, usually for reasons involving utility monsters. If you are one of these people, then you better learn to like it, because according to Harsanyi's Social Aggregation Theorem, any alternative can result in the supposedly Friendly AI making a choice that is bad for every member of the population. More formally,

That a bad result can happen in a given strategy is not a conclusive argument against preferring that strategy. Will it happen? What's the likelihood that it happens? What's the cost if it does happen?

The two alterna... (read more)

Reply
0AlexMennen
It's possible that the AI would just happen never to confront a situation where it would choose differently than everyone else would, but not reliably. If you had an AI that violated axiom 2, it would be tempting to modify it to include the special case "If X is the best option in expectation for every morally relevant agent, then do X." It seems hard to argue that such a modification would not be an improvement. And yet only throwing in that special case would make it no longer VNM-rational. Worse than a VNM-irrational agent is pretty bad. Because maximizing a weighted sum of utility functions does not have any comparably convincing failure modes. None that I've heard of anyway, and I'd be pretty shocked if you came up with a failure mode that did compete.
4buybuydandavis
You don't think utility monster is a comparably convincing failure mode? I think we just don't have data one way or the other.
0AlexMennen
Utility monster isn't a failure mode. It just messes with our intuitions because no one could imagine being a utility monster. Edit: At the time I made this comment, the wikipedia article on utility monsters incorrectly stated that a utility monster meant an agent that gets increasing marginal utility with respect to resources. Now that I know that a utility monster means an agent that gets much more utility from resources than other agents do, my response is that you can multiply the utility monster's utility function by a small coefficient, so that it no longer acts as a utility monster.
[-]Wei Dai50

Have you looked at some of the more recent papers in this literature (which generally have a lot more negative results than positive ones)? For example Preference aggregation under uncertainty: Savage vs. Pareto? I haven't paid too much attention to this literature myself yet, because the social aggregation results seem pretty sensitive to details of the assumed individual decision theory, which is still pretty unsettled. (Oh, I mentioned another paper here.)

Reply
0AlexMennen
Subjective uncertainty doesn't seem particularly relevant to Friendly AI, since the FAI could come up with a more accurate probability estimate than everyone else, and axiom 2 could refer to what everyone would want if they knew the probabilities as well as the FAI did. Do you have any examples of undesirable effects of the Pareto property that do not involve subjective uncertainty, or do you think subjective uncertainty is more important than I think it is?
0Wei Dai
I'm not sure. It probably depends on what "priors" really are and/or whether people have common priors. I have a couple of posts that explain these problems a bit more. But it does seem quite possible that the more recent results in the Bayesian aggregation literature aren't really relevant to FAI.
0private_messaging
Accurate probability estimate is a bit of oxymoron for anything other than certain class of problems where you have objective probability as a property of a non-linear system that has certain symmetries (e.g. die that bounces enough times).
3AlexMennen
How to measure accuracy
[-]Wei Dai40

What if we also add a requirement that the FAI doesn't make anyone worse off in expected utility compared to no FAI? That seems reasonable, but conflicts the other axioms. For example, suppose there are two agents: A gets 1 util if 90% of the universe is converted into paperclips, 0 utils otherwise, and B gets 1 util if 90% of the universe is converted into staples, 0 utils otherwise. Without an FAI, they'll probably end up fighting each other for control of the universe, and let's say each has 30% chance of success. An FAI that doesn't make one of them wo... (read more)

Reply
[-]Kaj_Sotala113

What if we also add a requirement that the FAI doesn't make anyone worse off in expected utility compared to no FAI?

Sounds obviously unreasonable to me. E.g. a situation where a person derives a large part of their utility from having kidnapped and enslaved somebody else: the kidnapper would be made worse off if their slave was freed, but the slave wouldn't become worse off if their slavery merely continued, so...

Reply
0Wei Dai
The way I said that may have been too much of a distraction from the real problem, which I'll restate as: considerations of fairness, which may arise from bargaining or just due to fairness being a terminal value for some people, can imply that the most preferred outcome lies on a flat part of the Pareto frontier of feasible expected utilities, in which case such preferences are not VNM rational and the result described in the OP can't be directly applied.
5Academian
I don't think that seems reasonable at all, especially when some agents want to engage in massively negative-sum games with others (like those you describe), or have massively discrete utility functions that prevent them from compromising with others (like those you describe). I'm okay with some agents being worse off with the FAI, if that's the kind of agents they are. Luckily, I think people, given time to reflect and grown and learn, are not like that, which is probably what made the idea seem reasonable to you.
4Wei Dai
Do you see CEV as about altruism, instead of cooperation/bargaining/politics? It seems to me the latter is more relevant, since if it's just about altruism, you could use CEV instead of CEV. So, if you don't want anyone to have an incentive to shut down an FAI project, you need to make sure they are not made worse off by an FAI. Of course you could limit this to people who actually have the power to shut you down, but my point is that it's not entirely up to you which agents the FAI can make worse off. Right, this could be another way to solve the problem: show that of the people you do have to make sure are not made worse off, their actual values (given the right definition of "actual values") are such that a VNM-rational FAI would be sufficient to not make them worse off. But even if you can do that, it might still be interesting and productive to look into why VNM-rationality doesn't seem to be "closed under bargaining". Also, suppose I personally (according to my sense of altruism) do not want to make anyone among worse off by my actions. Depending on their actual utility functions, it seems that my preferences may not be VNM-rational. So maybe it's not safe to assume that the inputs to this process are VNM-rational either?
3AlexMennen
Even if it's about bargaining rather than about altruism, it's still okay to have someone worse off under the FAI just so long as they would not be able to predict ahead of time that they wold get the short end of the stick. It's possible to have everyone benefit in expectation by creating an AI that is willing to make some people (who humans cannot predict the identity of ahead of time) worse off if it brings sufficient gain to the others.
2Wei Dai
I agree with this, which is why I said "worse off in expected utility" at the beginning of the thread. But I think you need "would not be able to predict ahead of time" in a fairly strong sense, namely that they would not be able to predict it even if they knew all the details of how the FAI worked. Otherwise they'd want to adopt the conditional strategy "learn more about the FAI design, and try to shut it down if I learn that I will get the short end of the stick". It seems like the easiest way to accomplish this is to design the FAI to explicitly not make certain people worse off, rather than depend on that happening as a likely side effect of other design choices.
1AlexMennen
I expect that with actual people, in practice, the FAI would leave no one worse off. But I wouldn't want to hardwire that into the FAI because then its behavior would be too status quo-dependent.
0cousin_it
What do you think about Eliezer's proposed solution of making the FAI's utility function depend on a coinflip outcome?
0[anonymous]
It seems like too much of a hack, but maybe it's not? Can you think of a general procedure for aggregating preferences that would lead to such an outcome (and also leads to sensible outcomes in other circumstances)?
0Wei Dai
It seems like too much of a hack, but maybe it's not? Can you think of a general procedure for aggregating preferences that would lead to such an outcome (and also leads to sensible outcomes in other circumstances)?
3cousin_it
Looking over my old emails, it seems that my email on Jan 21, 2011 proposed a solution to this problem. Namely, if the agents can agree on a point on the Pareto frontier given their current state of knowledge (e.g. the point where agent A and agent B each have 50% probability of winning), then they can agree on a procedure (possibly involving coinflips) whose result is guaranteed to be a Bayesian-rational merged agent, and the procedure yields the specified expected utilities to all agents given their current state of knowledge. Though you didn't reply to that email, so I guess you found it unsatisfactory in some way...
1Wei Dai
I must not have been paying attention to the decision theory mailing list at that time. Thinking it over now, I think technically it works, but doesn't seem very satisfying, because the individual agents jointly have non-VNM preferences, and are having to do all the work to pick out a specific mixed strategy/outcome. They're then using a coin-flip + VNM AI just to reach that specific outcome, without the VNM AI actually embodying their joint preferences. To put it another way, if your preferences can only be implemented by picking a VNM AI based on a coin flip, then your preferences are not VNM rational. The fact that any point on the Pareto frontier can be reached by a coin-flip + VNM AI seems more like a distraction to trying to figure how to get an AI to correctly embody such preferences.
0[anonymous]
What do you mean when you say the agents "jointly have non-VNM preferences"? Is there a definition of joint preferences?
[-]steven046140

I'd be curious to see someone reply to this on behalf of parliamentary models, whether applied to preference aggregation or to moral uncertainty between different consequentialist theories. Do the choices of a parliament reduce to maximizing a weighted sum of utilities? If not, which axiom out of 1-3 do parliamentary models violate, and why are they viable despite violating that axiom?

Reply
4Qiaochu_Yuan
Can you be more specific about what you mean by a parliamentary model? (If I had to guess, though, axiom 1.)
4steven0461
This and models similar to it.
4Qiaochu_Yuan
Interesting. A parliamentary model applied to moral uncertainty definitely fails axiom 1 if any of the moral theories you're aggregating isn't VNM-rational. It probably still fails axiom 1 even if all of the individual moral theories are VNM-rational because the entire parliament is probably not VNM-rational. That's okay from Bostom's point of view because VNM-rationality could be one of the things you're uncertain about.
3steven0461
What if it is not, in fact, one of the things you're uncertain about?
3Qiaochu_Yuan
Then I am not sure, because that blog post hasn't specified the model precisely enough for me to do any math, but my guess would be that the parliament fails to be VNM-rational. Depending on how the bargaining mechanism is set up, it might even fail to have coherent preferences in the sense that it might not always make the same choice when presented with the same pair of outcomes...
0Wei Dai
An advantage of parliamentary models is that you don't have to know the utility functions of the individual agents, but can just use them as black boxes that output decisions. This is useful for handling moral uncertainty when you don't know how to encode all the ethical theories you're uncertain about as utility functions over the same ontology. Let's say the parliament makes a Pareto optimal choice, in which case that choice is also made by maximizing some weighted sum of utilities (putting aside the coin flip issue). But the parliament doesn't reduce to maximizing that weighted sum of utilities, because the computation being done is likely very different. Saying that every method of making Pareto optimal choices reduces to maximizing a weighted sum of utilities would be like saying that every computation that outputs an integer greater than 1 reduces to multiplying a set of prime numbers.
[-]615C68A640

I don't see how I could agree with this conclusion :

But many people don't like this, usually for reasons involving utility monsters. If you are one of these people, then you better learn to like it, because according to Harsanyi's Social Aggregation Theorem, any alternative can result in the supposedly Friendly AI making a choice that is bad for every member of the population.

If both ways are wrong, then you haven't tried hard enough yet.

Well explained though.

Reply
8AlexMennen
The Social Aggregation Theorem doesn't just show that some particular way of aggregating utility functions other than by linear combination is bad; it shows that every way of aggregating utility functions other than by linear combination is bad.
[-]A.H.30

The link to Harsanyi's paper doesn't work for me. Here is a link that does, if anyone is looking for one: 

https://hceconomics.uchicago.edu/sites/default/files/pdf/events/Harsanyi_1955_JPE_v63_n4.pdf 

Reply
1momom2
Thanks! I wish the math hadn't broken down, it makes the post harder to read...
[-]DanielLC30

Axiom two reminds me of Simpson's paradox. I'm not sure how applicable it is, but I wouldn't be all that surprised so find an explanation that a violation of it this axiom perfectly reasonable. I don't suppose you have a set of more obvious axioms you could work with.

Reply
0Oscar_Cunningham
See my reply to 615C68A6.
0AlexMennen
There is no relation to Simpson's paradox. In Simpson's paradox, each of the data points comes from the same one-dimensional x-axis, so as you keep increasing x, you can run through all the data points in one group, go out the other side, and then get to another group of data points. In preference aggregation, there is no analogous meaningful way to run through one agent considering each possible state of the universe, keep going, and get to another agent considering each possible state of the universe.
3Oscar_Cunningham
Simpson's paradox can occur in discrete cases too, such as the example of a university showing a bias against women even though each of its constituent colleges was biased in their favour..
0AlexMennen
Good point. More relevantly, Simpson's paradox relies on different groups containing different values of the independent variable. If each group contains each independent variable in equal measure, Simpson's paradox cannot occur. The analogue of this in decision theory would be the probability distribution over outcomes. So if each agent has different beliefs about what A and B are, then it makes sense that everyone could prefer A over B but the FAI prefers B, but that's because the FAI has better information, and knows that at least some people would prefer B if they had better information about what the options consisted of. If everyone would prefer A over B given the FAI's beliefs, then that reason goes away, and the FAI should choose A. This latter situation is the one modeled in the post, and the former does not seem particularly relevant, since there's no point in asking which option someone prefers given bad information if you could also apply their utility function to a better-informed estimate of the probabilities involved.
[-]bryjnar30

Great post! I wish Harsanyi's papers were better known amongst philosophers.

Reply
[-]Qiaochu_Yuan30

Thanks for posting this! This is a fairly satisfying answer to my question from before.

Can you clarify which people you want to apply this theorem to? I don't think the relevant people should be the set of all humans alive at the time that the FAI decides what to do because this population is not fixed over time and doesn't have fixed utility functions over time. I can think of situations where I would want the FAI to make a decision that all humans alive at a fixed time would disagree with (for example, suppose most humans die and the only ones left happ... (read more)

Reply
6AlexMennen
I'm not entirely sure. My default answer to that is "all people alive at the time that the singularity occurs", although you pointed out a possible drawback to that (it incentivizes people to create more people with values similar to their own) in our previous discussion. This is really an instrumental question: What set of people should I suggest get to have their utility functions aggregated into the CEV so as to best maximize my utility? One possible answer is to aggregate the utilities of everyone who worked on or supported the FAI project, but I suspect that due to the influence of far thinking, that would actually be a terrible way to motivate people to work on FAI, and it should actually be much broader than that. I don't think it would be terribly problematic. "People in the future should get exactly what we currently would want them to get if we were perfectly wise and knew their values and circumstances" seems like a pretty good rule. It is, after all, what we want.
6Qiaochu_Yuan
And also incentivizes people to kill people with values dissimilar to their own! Fair enough. Hmm.
4AlexMennen
That's a pretty good nail in the coffin. Maybe all people alive at the time of your comment. Or at any point in some interval containing that time, possibly including up to the time the singularity occurs. Although again, these are crude guesses, not final suggestions. This might be a good question to think more about.
4Qiaochu_Yuan
It's not as bad as it sounds. Both arguments are also arguments against democracy, but I don't think they're knockdown arguments against democracy (although the general point that democracy can be gamed by brainwashing enough people is good to keep in mind, and I think is a point that Moldbug, for example, is quite preoccupied with). For example, killing people doesn't appear to be a viable strategy for gaining control of the United States at the moment. Although the killing-people strategy in the FAI case might look more like "the US decides to nuke Russia immediately before the singularity occurs."
5Jayson_Virissimo
Perhaps not, but it might help maintain control of the USG insofar as popularity increases the chances of reelection and killing (certain) people increases popularity.
0Academian
Dumb solution: an FAI could have a sense of justice which downweights the utility function of people who are killing and/or procreating to game their representation in AI's utility function, or something like that do disincentivize it. (It's dumb because I don't know how to operationalize justice; maybe enough people would not cheat and want to punish the cheaters that the FAI would figure that out.) Also, given what we mostly believe about moral progress, I think defining morality in terms of the CEV of all people who ever lived is probably okay... they'd probably learn to dislike slavery in the AI's simulation of them.
[-]timtyler30

A Friendly AI would have to be able to aggregate each person's preferences into one utility function. The most straightforward and obvious way to do this is to agree on some way to normalize each individual's utility function, and then add them up. But many people don't like this, usually for reasons involving utility monsters.

I should think most of those who don't like it do so because their values would be better represented by other approaches. A lot of those involved in the issue think they deserve more than a on-in-seven-billionth share of the fu... (read more)

Reply
4AlexMennen
They could just insist on a normalization scheme that is blatantly biased in favor of their utility function. In a theoretical sense, this doesn't cause a problem, since there is no objective way to define an unbiased normalization anyway. (of course, if everyone insisted on biasing the normalization in their favor, there would be a problem)
5timtyler
I think most of those involved realise that such projects tend to be team efforts - and therefore some compromises over values will be necessary. Anyway, I think this is the main difficulty for utilitarians: most people are not remotely like utilitarians - and so don't buy into their bizarre ideas about what the future should be like.
[-]JenniferRM20

I wonder how hard it would be to self-modify prior to the imposition of the sort of regime discussed here to be a counter-factual utility monster (along the lines of "I prefer X if Z and prefer not-X if not-Z") who very very much wants to be (and thus becomes?) an actual utility monster iff being a utility monster is rewarded. If this turns out to be easy then it seems like the odds of this already having happened in secret before the imposition of the utility-monster-rewarding-regime would need to be taken into account by those contemplating th... (read more)

Reply
0AlexMennen
Linearly combining utility functions does not force you to reward utility monsters. It just forces you to either be willing to sacrifice large amounts of others' utility for extremely large amounts of utility monster utility, or be unwilling to sacrifice small amounts of others' utility for somewhat large amounts of utility monster utility in the same ratio. The normalization scheme could require the range of all normalized utility functions to fit within certain bounds.
[-]A1987dM20

Does the theorem say anything about the sign of the c_k? Will they always all be positive? Will they always all be non-negative?

Reply
6AlexMennen
Under Harsanyi's original axioms, you cannot say anything about the signs of the coefficients. My axioms are slightly stronger, but I think still not quite enough. However, if you make the even stronger (but still reasonable, I think) assumption that the agents' utility functions are linearly independent, then you can prove that all of the coefficients are non-negative. This is because the linear independence allows you create situations where each agent prefers A to B by arbitrarily specifiable relative amounts. As in, for all agents k, we can create choices A and B such that every agent prefers A to B, but the margin by which every agent other than k prefers A to B is arbitrarily small compared to the margin by which k prefers A to B, so since FAI prefers A to B, c_k must be nonnegative.
[-]Kindly10

Being fair is not, in general, a VNM-rational thing to do.

Suppose you have an indivisible slice of pie, and six people who want to eat it. The fair outcome would be to roll a die to determine who gets the pie. But this is a probabilistic mixture of six deterministic outcomes which are equally bad from a fairness point of view.

Preferring a lottery to any of its outcomes is not VNM-rational (pretty sure it violates independence, but in any case it's not maximizing expected utility).

We can make this stronger by supposing some people like pie more than others... (read more)

Reply
0AlexMennen
I'm pretty sure it's possible to reach the same conclusion by removing the requirement that the aggregation be VNM-rational and strengthening axiom 2 to say that the aggregation must be Pareto-optimal with respect to all prior probability distributions over choices the aggregation might face. That is, "given any prior probability distribution over pairs of gambles the aggregation might have to choose between, there is no other possible aggregation that would be better for every agent in the population in expectation." It's possible we could even reach the same conclusion just by using some such prior distribution with certain properties, instead of all such distributions.
2Kindly
I don't understand what your strengthened axiom means. Could you give an example of how, say, the take-the-min-of-all-expected-utilities aggregation fails to satisfy it? (Or if it doesn't I suppose it would be a counterexample, but I'm not insisting on that)
6AlexMennen
Lets say there are 3 possible outcomes: A, B, and C, and 2 agents: x and y. The utility functions are x(A)=0, x(B)=1, x(C)=4, y(A)=4, y(B)=1, y(C)=0. One possible prior probability distribution over pairs of gambles is that there is a 50% chance that the aggregation will be asked to choose between A and B, and a 50% chance that the aggregation will be asked to choose between B and C (in this simplified case, all the anticipated "gambles" are actually certain outcomes). Your maximin aggregation would choose B in each case, so both agents anticipate an expected utility of 1. But the aggregation that maximizes the sum of each utility function would choose A in the first case and C in the second, and each agent would anticipate an expected utility of 2. Since both agents could agree that this aggregation is better than maximin, maximin is not Pareto optimal with respect to that probability distribution. Upvoted for suggesting a good example. I had suspected my explanation might be confusing, and I should have thought to include an example.
0Kindly
Thank you, I understand it now.
[-]Academian00

Thanks for writing this up!

Reply
[-]Douglas_Knight00

It is worth mentioning that Rawl's later Veil of Ignorance forces him to satisfy Harsanyi's axioms and Rawl's conclusions are a math error.

Reply
0AlexMennen
Harsanyi's axioms seem self-evidently desirable on their own. I didn't claim that they were a consequence of the Veil of Ignorance.
[-]Vaniver00

Edit: conclusion here. I misinterpreted axiom 2 as weaker than it is; I now agree that the axioms imply the result (though I interpret the result somewhat differently).

I don't think you can make the broad analogy between what you're doing and what Harsanyi did that you're trying to make.

Harsanyi's postulate D is doing most of the work. Let's replace it with postulate D': if at least two individuals prefer situation X to situation Y, and none of the other individuals prefer Y to X, then X is preferred to Y from a social standpoint.

D' is weaker; the weighted... (read more)

Reply
2AlexMennen
You were looking at Harsanyi's explanation of a previous, similar theorem by Fleming, in section II of his paper. He proves the theorem I explained in the post in section III. My axiom 2 was meant to include decisions involving uncertainty, like Harsanyi's postulates but unlike Fleming's postulates. Sorry if I did not make that clear.
4Vaniver
Your axioms being meant to include something doesn't mean that they include something! Your axioms do not imply Harsanyi's, and so your proof is fatally flawed. Right now, Axiom 1 only means that each agent needs to individually have a scoring system for outcomes which satisfies the VNM axioms (basically, you can map outcomes to reals, and those reals encode probabilistic preferences). Axiom 2 is really weak, and Axiom 3 is really weak. My social utility of T satisfies Axioms 1, 2 and 3 for Alice, Bob, and Charlie: 1. Alice, Bob, and Charlie each have utility functions and T is a utility function. Agents make probabilistic gambles accordingly. 2. If all of Alice, Bob, and Charlie prefer an outcome to another outcome, then so does T. (The only example of this is the preference for Z over W.) 3. There is an example where Alice, Bob, and Charlie all share a preference: Z over W. Note that every agent is indifferent between W and W, and that every agent prefers Z to W. We compare the gambles pZ+(1-p)W and pW+(1-p)W, and note that T satisfies the property that the first gamble is preferred to the second gamble for arbitrarily small p (as the utility of the first gamble is p, and the utility of the second gamble is 0), and that T is indifferent between them for p=0. T, of course, is not a linear combination of Alice, Bob, and Charlie's utility functions. Is T a counterexample to your theorem? If not, why not?
4AlexMennen
T does not satisfy axiom 2 because Alice, Bob, and Charlie all prefer the gamble .5X+.5Y over W, but T is indifferent between .5X+.5Y and W. As I said, axiom 2 includes decisions under uncertainty. The VNM axioms don't even make a distinction between known outcomes and gambles, so I assumed that would be understood as the default.
2Vaniver
Ah! I was interpreting "choice" as "outcome," rather than "probabilistic combination of outcomes," and with the latter interpretation axiom 2 becomes much stronger. I still don't think it's strong enough, though: it appears to me that U still satisfies axiom 2, despite not being a linear combination of the utilities. As well, if I add Diana, who has utility (0,0,0,1), then T appears to serve as a social welfare function for Alice, Bob, Charlie, and Diana. I should note that I suspect that's a general failure mode: take any utility function, and add an agent to the pool who has that utility function. That agent is now a candidate for the social welfare function, as it now satisfies the first two axioms and might satisfy the third. (Alternatively, appoint any agent already in the pool as the social welfare function; the first two axioms will be satisfied, and the third will be unchanged.)
4AlexMennen
That is correct. But in a case like that, the aggregate utility function is a linear combination of the original utility functions where all but one of the coefficients are 0. Being a linear combination of utility functions is not a strong enough requirement to rule out all bad aggregations.
4Vaniver
First, thanks for your patience. Conclusion: I don't agree with Harsanyi's claim that the linear combination of utility functions is unique up to linear transformations. I agree it is unique up to affine transformations, and the discrepancy between my statement and his is explained by his comment "on the understanding that the zero point of the social welfare function is appropriately chosen." (Why he didn't explicitly generalize to affine transformations is beyond me.) I don't think the claim "the utility function can be expressed as a linear combination of the individual utility functions" is particularly meaningful, because it just means that the aggregated utility function must exist in the space spanned by the individual utility functions. I'd restate it as: (Because, as per VNM, all values are comparable.) Also, note that this might not be a necessary condition for friendliness, but it is a necessary condition for axiom 2-ness. Notes: I've been representing the utilities as vectors, and it seems like moving to linear algebra will make this discussion much cleaner. Suppose the utility vector for an individual is a row vector. We can combine their preferences into a matrix P=[A;B;C]. In order to make a counterexample, we need a row vector S which 1) is linearly independent of P, that is, rank[P;S] =/= rank[P]. Note that if P has rank equal to the number of outcomes, this is impossible; all utility functions can be expressed as linear combinations. In our particular example, the rank of P is 3, and there are 4 outcomes, so S=null[P]=[-1,0,0,0], and we can confirm that rank[P;S]=4. (Note that for this numerical example, S is equivalent to a affinely transformed C, but I'm not sure if this is general.) We also need S to 2) satisfy any preferences shared by all members of P. We can see gambles as column vectors, with each element being the probability that a gamble leads to a particular outcome; all values should be positive and sum to one. We can compare ga
5AlexMennen
I'm not quite sure what you mean. Are you talking about the fact that you can add a constant to utility function without changing anything important, but that a constant is not necessarily a linear combination of the utility functions to be aggregated? For that reason, it might be best to implicitly include the constant function in any set of utility functions when talking about whether or not they are linearly independent; otherwise you can change the answer by adding a constant to one of them. Also, where did Harsanyi say that? Yes, that's what it means. I don't see how that makes it unmeaningful. Agreed that linear algebra is a natural way to approach this. In fact, I was thinking in similar terms. If you replace axiom 3 with the stronger assumption that the utility functions to be aggregated, along with the constant function, are linearly independent (which I think is still reasonable if there are an infinite number of outcomes, or even if there are just at least 2 more outcomes than agents), then it is fairly easy to show that sharing preferences requires the aggregation to be a linear combination of the utility functions and the constant function. Let K represent the row vector with all 1s (a constant function). Let "pseudogamble" refer to column vectors whose elements add to 1 (Kx = 1). Note that given two pseudogambles x and y, we can find two gambles x' and y' such that for any agent A, A(x-y) has the same sign as A(x'-y') by mixing the pseuogambles with another gamble. For instance, if x, y, and z are outcomes, and A(x) > A(2y-z), then A(.5x+.5z) > A(.5(2y-z)+.5z) = A(y). So the fact that I'll be talking about pseudogambles rather than gambles is not a problem. Anyway, if the initial utility functions and K are linearly independent, then the aggregate not being a linear combination of the initial utility functions and K would mean that the aggregate, K, and the initial utility functions all together are linearly independent. Given a linearly independen
3Vaniver
Immediately before the statement of Theorem I in section III. In my mind, there's a meangingful difference between construction and description- yes, you can describe any waveform as an infinite series of sines and cosines, but if you actually want to build one, you probably want to use a finite series. And this result doesn't exclude any exotic methods of constructing utility functions; you could multiply together the utilities of each individual in the pool and you'd end up with an aggregate utility function that could be expressed as a linear combination of the individual utilities (and the ones vector), with the weights changing every time you add another individual to the pool or add another outcome to be considered. More relevant to the discussion, though, is the idea of the aggregator should not introduce novel preferences. This is an unobjectionable conclusion, I would say, but it doesn't get us very far: if there are preferences in the pool that we want to exclude, like a utility monster's, setting their weight to 0 is what excludes their preferences, not abandoning linear combinations, and if the system designer has preferences about "fairness" or so on, then so long as one of the agents in the pool has those preferences, the system designer can incorporate those preferences just by increasing their weight in the combination. But in both cases, the aggregator would probably be created through another function, and then so long as it does not introduce novel preferences it can be described as a linear combination. Instead of arguing about weights, we may find it more fruitful to argue about meta-weights, even though there is a many-to-one mapping (for any particular instance) from meta-weights to weights. I'd recommend the use of "e" for the ones vector, and if the elements add to 1, it's not clear to me why it's a "pseudogamble" rather than a "gamble," if one uses the terminology that column vectors where only a single element is 1 are "outcomes." I f
1AlexMennen
Unlikely, unless there are at least as many agents as outcomes. Yes. In fact, I think something like that will be necessary. For example, suppose there is a population of two agents, each of which has a "hedon function" which specifies their agent-centric preferences. One of the agents is an egoist, so his utility function is his hedon function. The other agent is an altruist, so his utility function is the average of his and the egoist's hedon functions. If you add up the two utility functions, you find that the egoist's hedon function gets three times the weight of the altruist's hedon function, which seems unfair. So we would want to give extra weight to the altruist's utility function (you could argue that in this example you should use only the altruist's utility function). It may contain negative elements.
0Vaniver
It's unlikely that the weights of existing agents would change under either of those cases, or that the multiplication could be expressed as a weighted sum, or that the multiplication would have axiom 2-ness? Indeed. The problem is more general- I would classify the parts as "internal" and "external," rather than agent-centric and other, because that makes it clearer that agents don't have to positively weight each other's utilities. If you have a 'maltruist' whose utility is his internal utility minus the egoist's utility (divided by two to normalize), we might want to balance their weight and the egoist's weight so that the agents' internal utilities are equally represented in the aggregator. Such meta-weight arguments, though, exist in an entirely different realm from this result, and so this result has little bearing on those arguments (which is what people are interested in when they resist the claim that social welfare functions are linear combinations of individual utility). Ah! Of course.
2AlexMennen
Unlikely that the multiplication could be expressed as a weighted sum (and hence by extension, also unlikely it would obey axiom 2).
0Vaniver
I agree in general, because we would need the left inverse of the combined linearly independent individual utilities and e, and that won't exist. We do have freedom to affinely transform the individual utilities before taking their element-wise product, though, and that gives us an extra degree of freedom per agent. I suspect we can do it so long as the number of agents is at least half the number of outcomes.
0AlexMennen
Oh, I see what you mean. It should be possible to find some affinely transformed product that is also a linear combination if the number of agents is at least half the number of outcomes, but some arbitrary affinely transformed product is only likely to also be a linear combination if the number of agents is at least the number of outcomes.
2Vaniver
Right, I just noticed that. So T is out as a counterexample, and likewise U is just Charlie's utility. Attempting to build another counterexample.
Moderation Log
90Comments