A Friendly AI would have to be able to aggregate each person's preferences into one utility function. The most straightforward and obvious way to do this is to agree on some way to normalize each individual's utility function, and then add them up. But many people don't like this, usually for reasons involving utility monsters. If you are one of these people, then you better learn to like it, because according to Harsanyi's Social Aggregation Theorem, any alternative can result in the supposedly Friendly AI making a choice that is bad for every member of the population. More formally,
Axiom 1: Every person, and the FAI, are VNM-rational agents.
Axiom 2: Given any two choices A and B such that every person prefers A over B, then the FAI prefers A over B.
Axiom 3: There exist two choices A and B such that every person prefers A over B.
(Edit: Note that I'm assuming a fixed population with fixed preferences. This still seems reasonable, because we wouldn't want the FAI to be dynamically inconsistent, so it would have to draw its values from a fixed population, such as the people alive now. Alternatively, even if you want the FAI to aggregate the preferences of a changing population, the theorem still applies, but this comes with it's own problems, such as giving people (possibly including the FAI) incentives to create, destroy, and modify other people to make the aggregated utility function more favorable to them.)
Give each person a unique integer label from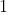 to
, where
is the number of people. For each person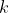
, let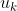
be some function that, interpreted as a utility function, accurately describes
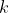's preferences (there exists such a function by the VNM utility theorem). Note that I want
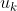to be some particular function, distinct from, for instance,
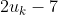, even though
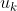and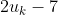
represent the same utility function. This is so it makes sense to add them.
Theorem: The FAI maximizes the expected value of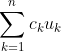 , for some set of scalars
.
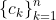Actually, I changed the axioms a little bit. Harsanyi originally used “Given any two choices A and B such that every person is indifferent between A and B, the FAI is indifferent between A and B” in place of my axioms 2 and 3 (also he didn't call it an FAI, of course). For the proof (from Harsanyi's axioms), see section III of Harsanyi (1955), or section 2 of Hammond (1992). Hammond claims that his proof is simpler, but he uses jargon that scared me, and I found Harsanyi's proof to be fairly straightforward.
Harsanyi's axioms seem fairly reasonable to me, but I can imagine someone objecting, “But if no one else cares, what's wrong with the FAI having a preference anyway. It's not like that would harm us.” I will concede that there is no harm in allowing the FAI to have a weak preference one way or another, but if the FAI has a strong preference, that being the only thing that is reflected in the utility function, and if axiom 3 is true, then axiom 2 is violated.
proof that my axioms imply Harsanyi's: Let A and B be any two choices such that every person is indifferent between A and B. By axiom 3, there exists choices C and D such that every person prefers C over D. Now consider the lotteries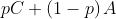 and
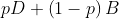, for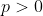
. Notice that every person prefers the first lottery to the second, so by axiom 2, the FAI prefers the first lottery. This remains true for arbitrarily small
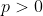, so by continuity, the FAI must not prefer the second lottery for
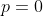; that is, the FAI must not prefer B over A. We can “sweeten the pot” in favor of B the same way, so by the same reasoning, the FAI must not prefer A over B.
So why should you accept my axioms?
Axiom 1: The VNM utility axioms are widely agreed to be necessary for any rational agent.
Axiom 2: There's something a little rediculous about claiming that every member of a group prefers A to B, but that the group in aggregate does not prefer A to B.
Axiom 3: This axiom is just to establish that it is even possible to aggregate the utility functions in a way that violates axiom 2. So essentially, the theorem is “If it is possible for anything to go horribly wrong, and the FAI does not maximize a linear combination of the people's utility functions, then something will go horribly wrong.” Also, axiom 3 will almost always be true, because it is true when the utility functions are linearly independent, and almost all finite sets of functions are linearly independent. There are terrorists who hate your freedom, but even they care at least a little bit about something other than the opposite of what you care about.
At this point, you might be protesting, “But what about equality? That's definitely a good thing, right? I want something in the FAI's utility function that accounts for equality.” Equality is a good thing, but only because we are risk averse, and risk aversion is already accounted for in the individual utility functions. People often talk about equality being valuable even after accounting for risk aversion, but as Harsanyi's theorem shows, if you do add an extra term in the FAI's utility function to account for equality, then you risk designing an FAI that makes a choice that humanity unanimously disagrees with. Is this extra equality term so important to you that you would be willing to accept that?
Remember that VNM utility has a precise decision-theoretic meaning. Twice as much utility does not correspond to your intuitions about what “twice as much goodness” means. Your intuitions about the best way to distribute goodness to people will not necessarily be good ways to distribute utility. The axioms I used were extremely rudimentary, whereas the intuition that generated "there should be a term for equality or something" is untrustworthy. If they come into conflict, you can't keep all of them. I don't see any way to justify giving up axioms 1 or 2, and axiom 3 will likely remain true whether you want it to or not, so you should probably give up whatever else you wanted to add to the FAI's utility function.
Citations:
Harsanyi, John C. "Cardinal welfare, individualistic ethics, and interpersonal comparisons of utility." The Journal of Political Economy (1955): 309-321.
Hammond, Peter J. "Harsanyi’s utilitarian theorem: A simpler proof and some ethical connotations." IN R. SELTEN (ED.) RATIONAL INTERACTION: ESSAYS IN HONOR OF JOHN HARSANYI. 1992.