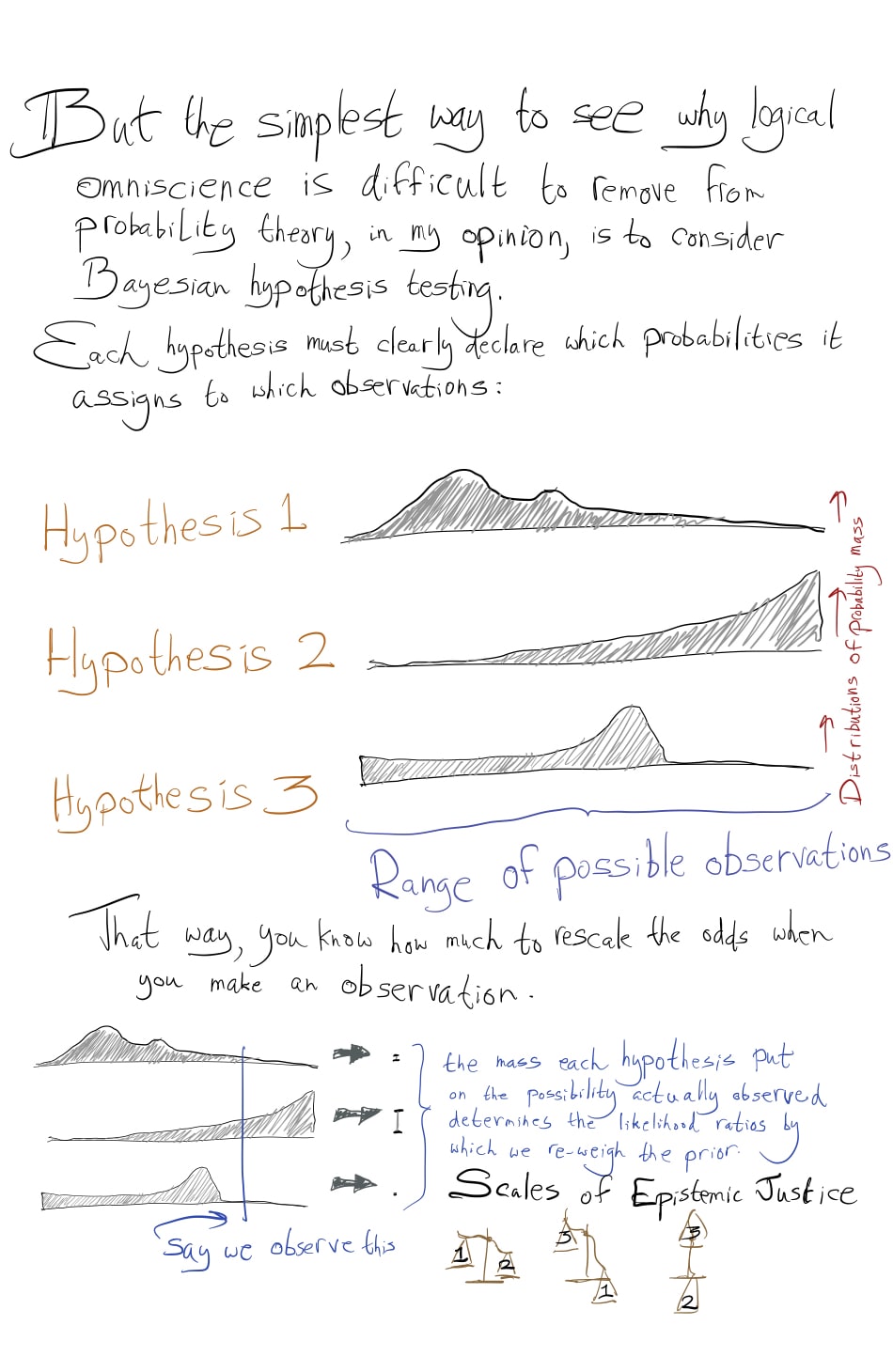
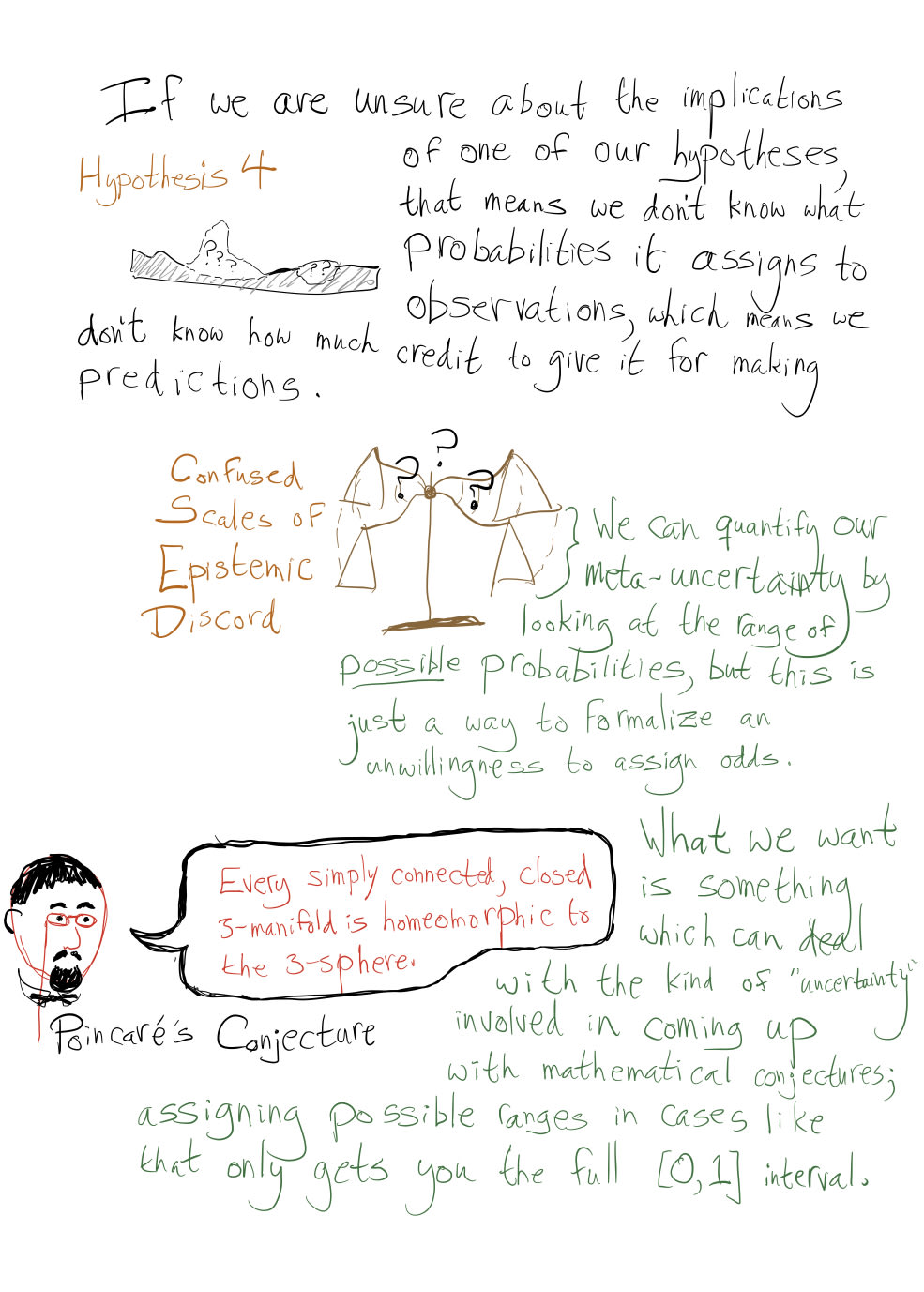
An Untrollable Mathematician Illustrated

abramdemski

This is great. I consistently keep wanting to read the title as "Uncontrollable Mathematician," which I'm excited about as a band name.

[-]ryan_b7y80

Perhaps if we specify a different rule that only solves the problem of updating on negative information, you could have an "Un-Con-Trollable Mathematician."

[-]nostalgebraist7y240

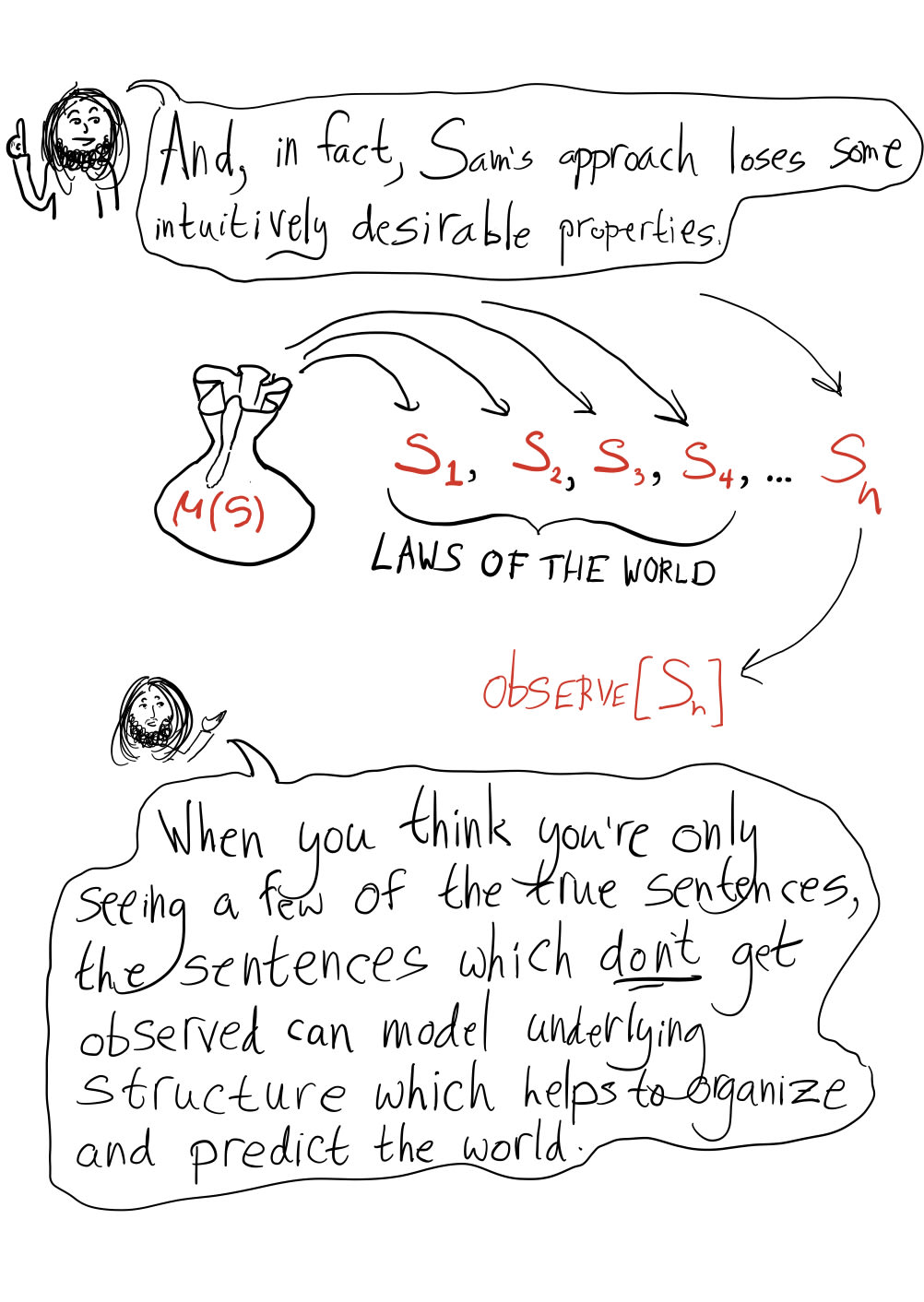
This prior isn’t trollable in the original sense, but it is trollable in a weaker sense that still strikes me as important. Since $μ$ must sum to 1, only finitely many sentences $S$ can have $μ (S) > ϵ$ for a given $ϵ > 0$ . So we can choose some finite set of “important sentences” and control their oscillations in a practical sense, but if there’s any $ϵ > 0$ such that we think oscillations across the range $(ϵ, 1 - ϵ)$ are a bad thing, all but finitely many sentences can exhibit this bad behavior.

It seems especially bad that we can only prevent “up-to- $ϵ$ trolling” for finite sets of sentences, since in PA (or whatever) there are plenty of countable sets of sentences that seem “essentially the same” (like the ones you get from an induction argument), and it feels very unnatural to choose finite subsets of these and distinguish them from the others, even (or especially?) if we pretend we have no prior knowledge beyond the axioms.

[-]Hazard7y210

This was incredibly enjoyable to read! I think you did a very good job of making it easy to read without dumbing it down. Though I'm not well versed in the core math of this post, I still feel like I managed to get some useful gist from it, and I also don't feel like I've been tricked into thinking I understand more than I do.

[-]habryka6yΩ6160Nomination for 2018 Review

I think this post, together with Abram's other post "Towards a new technical explanation" actually convinced me that a bayesian approach to epistemology can't work in an embedded context, which was a really big shift for me.

[-]TurnTrout6yΩ5150Nomination for 2018 Review

Abram's writing and illustrations often distill technical insights into accessible, fun adventures. I've come to appreciate the importance and value of this expository style more and more over the last year, and this post is what first put me on this track. While more rigorous communication certainly has its place, clearly communicating the key conceptual insights behind a piece of work makes those insights available to the entire community.

[-]Ben Pace7y120

(this is so awesome and it helps give me intuitions about Gödel's theorem and how mathematics happens and stuff)

I didn't parse the final sentence?

Logical induction (which is untrollable but not exactly a Bayesian probability distribution) is still the gold standard for logical uncertainty, but perhaps the number of desirable properties we can get by specifying simple sampling processes.

It feels like it should say 'but perhaps the number of desirable properties we can get by specifying simple sampling processes is X' but is missing the final clause, or something.

Edit: This has been fixed now :-)

[-]abramdemski7y60

Right, whoops.

It should have said "... by specifying simple sampling processes will increase as we push further in the direction Sam has opened up."

[-]DanielFilan7y60

Further bug: I can now see both the old final image and the new final image.

[-]abramdemski7y30

Wow, that's weird, I **don't** see both when I try to edit the draft. Only in the non-editing view.

[-]habryka7y60

Sorry for that, fixed it!

[-]Ben Pace7y30

Wow. Oli's on it.

[-]Ben Pace7y90

I curated this post because:

The explanation itself was very clear - a serious effort had been made to explain this work and related ideas.
In the course of explaining a single result, it helps give strong intuitions about a wide variety of related areas in math and logic, which are very important for alignment research.
It was really fun to read; the drawings are very beautiful.

Biggest hesitations I had with curating:

It wasn't clear to me that the main argument the post makes regarding the untrollable mathematicians is itself a huge result in agent foundations research.

This wasn't a big factor for me though, as just making transparent all of the mental moves in achieving this result helps the reader with seeing / learning the mental models used throughout this research area.

[-]Jameson Quinn5y70Review for 2018 Review

This is truly one of the best posts I've read. It guides the reader through a complex argument in a way that's engaging and inspiring. Great job.

[-]hwold7y70

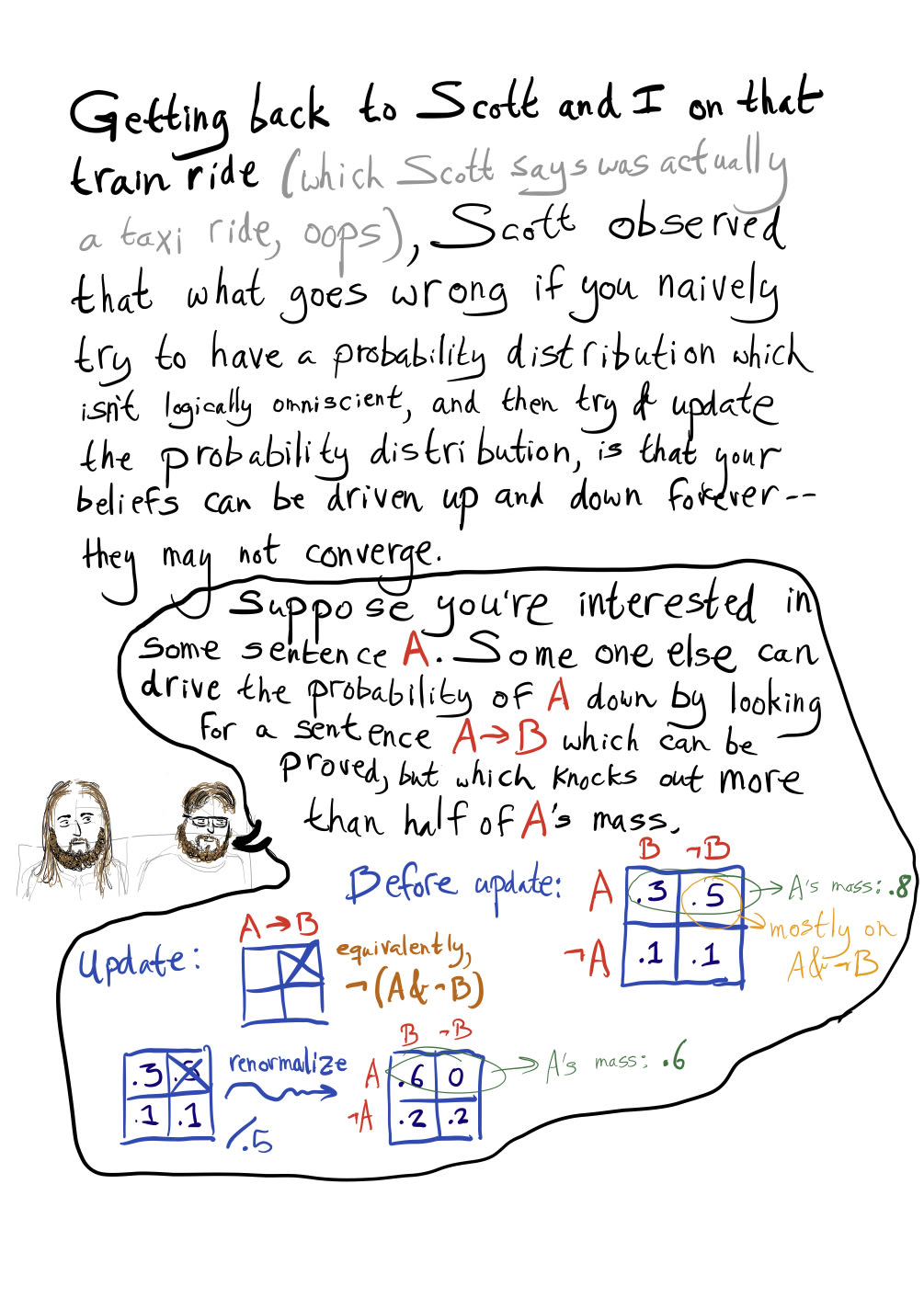
I don’t understand where that 1/2 comes from. Unless I have made a gross mistake P(A|A => B) < P(A) even if P(A&B) > P(A&not(B)). In your first example, if I swap P(AB) and P(A&not(B)) so that P(AB) = .5 and P(A&not(B))=.3 then P(A|A=>B) = .5/.7 ~ 0.71 < 0.8 = P(A).

[-]Chris_Leong7y51

This confused me as well. This being true ensures that the ratio P(A):P(not A) doubles at each step. But part of this comic seems to imply that being less than a half stops the trolling, when it should only stop the trolling from proceeding at such a fast-paced rate.

[-]rk7y70

I want to echo the other comments thanking you for making this lay-approachable and for the fun format!

I do find myself confused by some of the statements though. It may be that I have a root misunderstanding or that I am misreading some of the more quickly stated sentences.

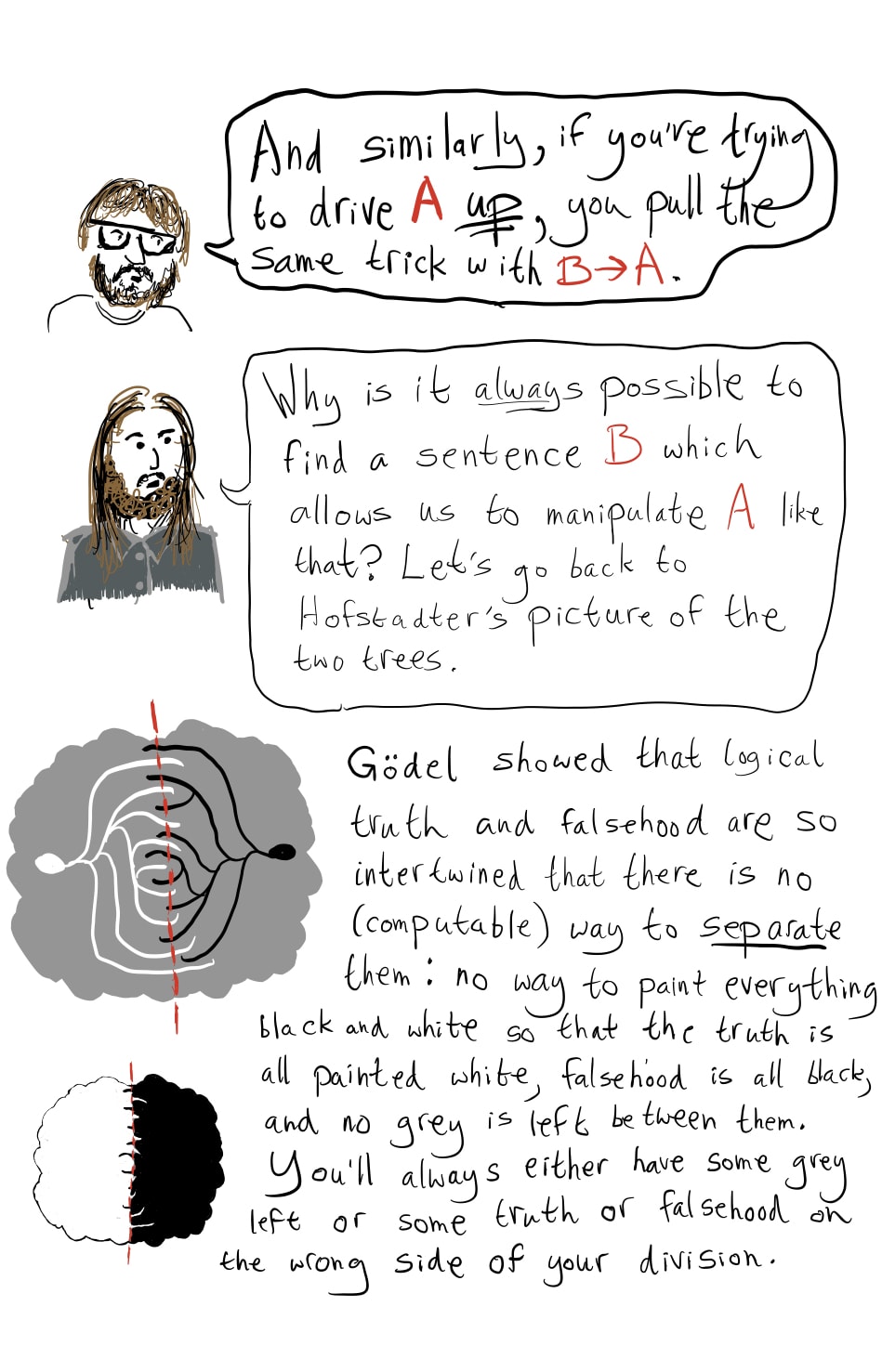
For example, when you talk about the trees of truth & falsehood and the gap in the middle: am I right in thinking of these trees as provability and non-provability? Rather than perhaps truth & falsehood

Also, in the existence proof for Bs such that $P (B | A) > \frac{1}{2}$ and we can prove $A \to B$ , you say that if B is a logical truth, A -> B must be provable, because anything implies a logical truth. It seems right to me that anything logically implies a logical truth. But surely we can't prove all logical truths from anything -- what if it's a truth in the grey area such that it can't be proved at all?

If someone can put me right, that would be great

[-]Dacyn7y60

Yes you are right that the first tree is provability, but I think the second tree is meant to be disprovability rather than non-provability. Similarly, when the OP later talks about "logical truths" and "logical falsehoods" it seems he really means "provable statements" and "disprovable statements" -- this should resolve the issue in your last paragraph, since if B is provable then so is A->B.

[-]rk7y10

disprovability rather than non-provability

Yeah, you're definitely right there. Oops, me.

Similarly, when the OP later talks about "logical truths" and "logical falsehoods" it seems he really means "provable statements" and "disprovable statements" -- this should resolve the issue in your last paragraph, since if B is provable then so is A->B

If that's the case, then how does Goedel kick in? He then says, nothing can separate logical truth from logical falsehood. But if he means provability and disprovability, then trivially they can be separated

[-]Dacyn7y40

Here "separation" would mean that there is an algorithm which inputs any statement and outputs either "yes" or "no", such that the algorithm returns "yes" on all inputs that are provable statements and "no" on all inputs that are disprovable statements. But the algorithm also has to halt on all possible inputs, not just the ones that are provable or disprovable. Such a separation algorithm cannot exist (I am not sure if this follows from Gödel's theorem or requires a separate diagonalization argument). This is the result needed in that step of the argument.

[-]rk7y10

Ah, so I was quite wrong when I said "trivially they can be separated". Cos we only have semi-decision procedures for provability and disprovability!

Thanks for helping me with this

[-]cousin_it7y70

Great explanation! I read your earlier post on IAFF where the whole thing was explained in one sentence, and it was quite clear, but seeing it in pictures is much more fun. Maybe this is also why the Sequences were fun to read - they explained simple ideas but in a very fancy cursive font :-)

[-]Connor_Flexman7y60

I am confused as to how the propositional consistency and $observe []$ function work together to prevent the trolling in the final step. Suppose I do try to find pairs of sentences such that I can show $(A \Rightarrow B_{i})$ and also $\neg B_{i}$ to drive $A$ down. Does this fail because you are postulating non-adversarial sampling, as ESRogs mentions? Or is there some other reason why propositional consistency is important here?

[-]Diffractor7y100

There's a misconception, it isn't about finding sentences of the form $A \to B_{i}$ and $\neg B_{i}$ , because if you do that, it immediately disproves $A$ . It's actually about merely finding many instances of $A \to B_{i}$ where $P (B_{i} | A)$ has $< \frac{1}{2}$ probability, and this lowers the probability of $A$ . This is kind of like how finding out about the Banach-Tarski paradox (something you assign low probability to) may lower your degree of belief in the axiom of choice.

The particular thing that prevents trolling is that in this distribution, there's a fixed probability of drawing $A$ on the next round no matter how many implications and $B$ 's you've found so far. So the way it evades trolling is a bit cheaty, in a certain sense, because it believes that the sequence of truth or falsity of math sentences that it sees is drawn from a certain fixed distribution, and doesn't do anything like believing that it's more likely to see a certain class of sentences come up soon.

[-]Ben Pace7y50

(I fixed your LaTex. FYI whatever your comment looks like before you post, is what it will look like after. Use ctrl-4 or cmd-4 for LaTex, depending on whether you're using a PC or a Mac.)

[-]ESRogs7y60

Propositional consistency lets us express constraints between sentences (such as " $A$ and $B$ cannot both be true") as sentences (such as " $\neg (A & B)$ ") in a way the prior understands and correctly enforces.

Any branch contradicting an already-stated constraint is clipped off the tree of possible sequences of sentences.

The probability of any sentence $S$ which is consistent with everything seen so far can't go below $μ (S)$ or above $1 - μ (\neg S)$ , since $S$ or $\neg S$ can be drawn next. So, no trolling.

How do I know whether $S$ is consistent with everything seen so far. Doesn't that presuppose logical omniscience?

Or does consistency here only mean that it doesn't violate any explicitly stated constraints (such that I don't have to know all the implications of all the sentences I've seen so far and whether they contradict $S$ )?

[-]Diffractor7y150

There's a difference between "consistency" (it is impossible to derive X and notX for any sentence X, this requires a halting oracle to test, because there's always more proof paths), and "propositional consistency", which merely requires that there are no contradictions discoverable by boolean algebra only. So A^B is propositionally inconsistent with notA, and propositionally consistent with A. If there's some clever way to prove that B implies notA, it wouldn't affect the propositional consistency of them at all. Propositional consistency of a set of sentences can be verified in exponential time.

[-]Chris_Leong7y30

Since propositional consistency is weaker than consistency our prior may distribute some probability to cases that are contradictory. I guess that's considered acceptable because the aim is to make the prior non-trollable, rather than good.

[-]cata7y50

Thank you for making this! The format held my attention well, so I understood a lot whereas I might have zoned out and left if the same material had been presented more traditionally. I'm going to print it out and distribute it at work -- people like zines there.

[-]Dacyn7y40

Maybe I am not sure why this mathematician is considered to be untrollable? It seems the same or a similar algorithm could drive his probabilities up and down arbitrarily within the interval $[μ (S), 1 - μ (- S)]$ . If this is true, then his beliefs at any stage are essentially arbitrary with respect to this restriction. But isn't that basically the same as saying that if the statement hasn't been proven or disproven yet, then his beliefs don't give any meaningful (non-trollable) further information as to whether the statement is true?

[-]Diffractor7y30

The beliefs aren't arbitrary, they're still reasoning according to a probability distribution over propositionally consistent "worlds". Furthermore, the beliefs converge to a single number in the limit of updating on theorems, even if the sentence of interest is unprovable. Consider some large but finite set S of sentences that haven't been proved yet, such that the probability of sampling a sentence in that set before sampling the sentence of interest "x", is very close to 1. Then pick a time N, that is large enough that by that time, all the logical relations between the sentences in S will have been found. Then, with probability very close to 1, either "x" or "notx" will be sampled without going outside of S.

So, if there's some cool new theorem that shows up relating "x" and some sentence outside of S, like "y->x", well, you're almost certain to hit either "x" or "notx" before hitting "y", because "y" is outside S, so this hot new theorem won't affect the probabilities by more than a negligible amount.

Also I figured out how to generalize the prior a bit to take into account arbitrary constraints other than propositional consistency, though there's still kinks to iron out in that one. Check this.

[-]ESRogs7y40

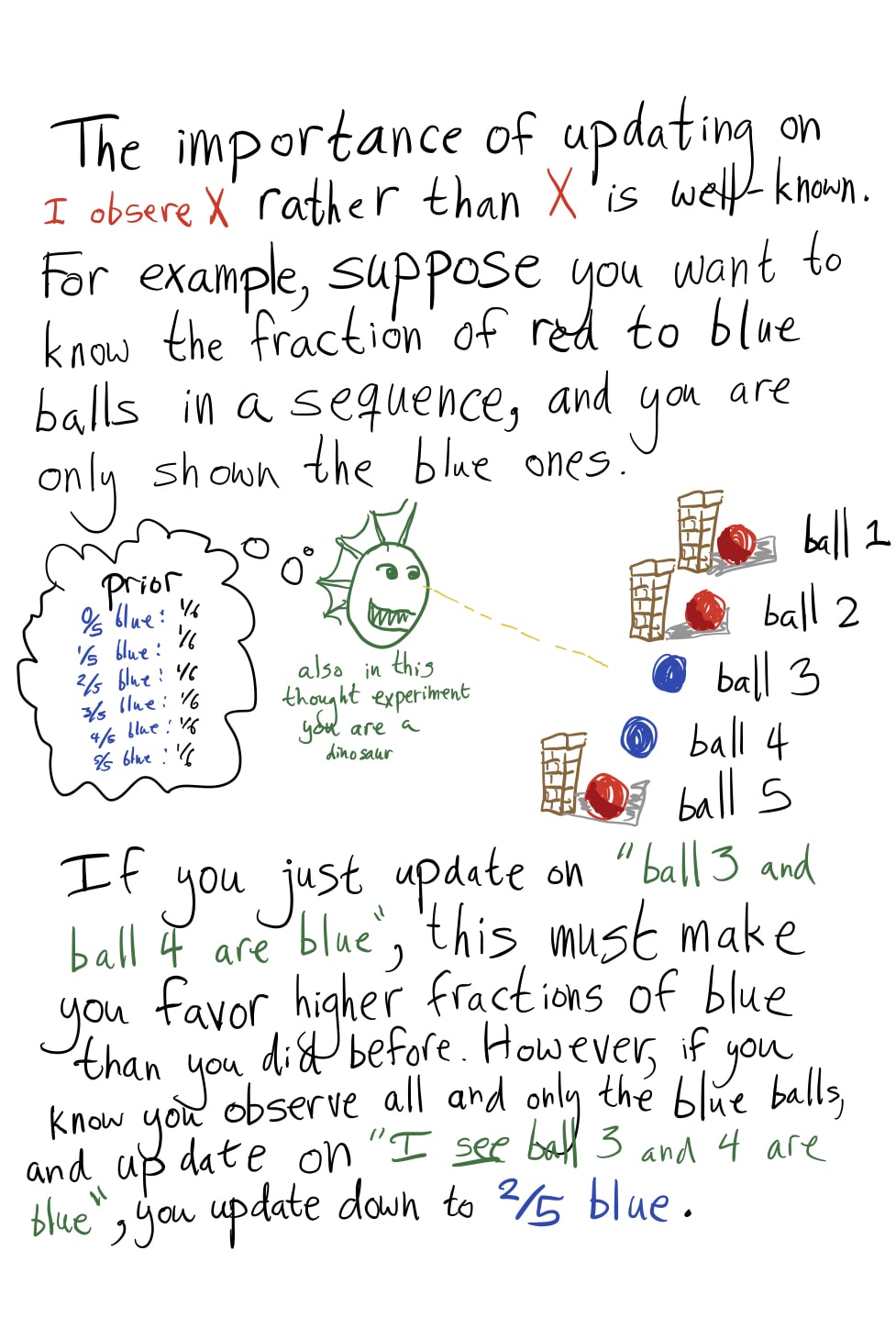
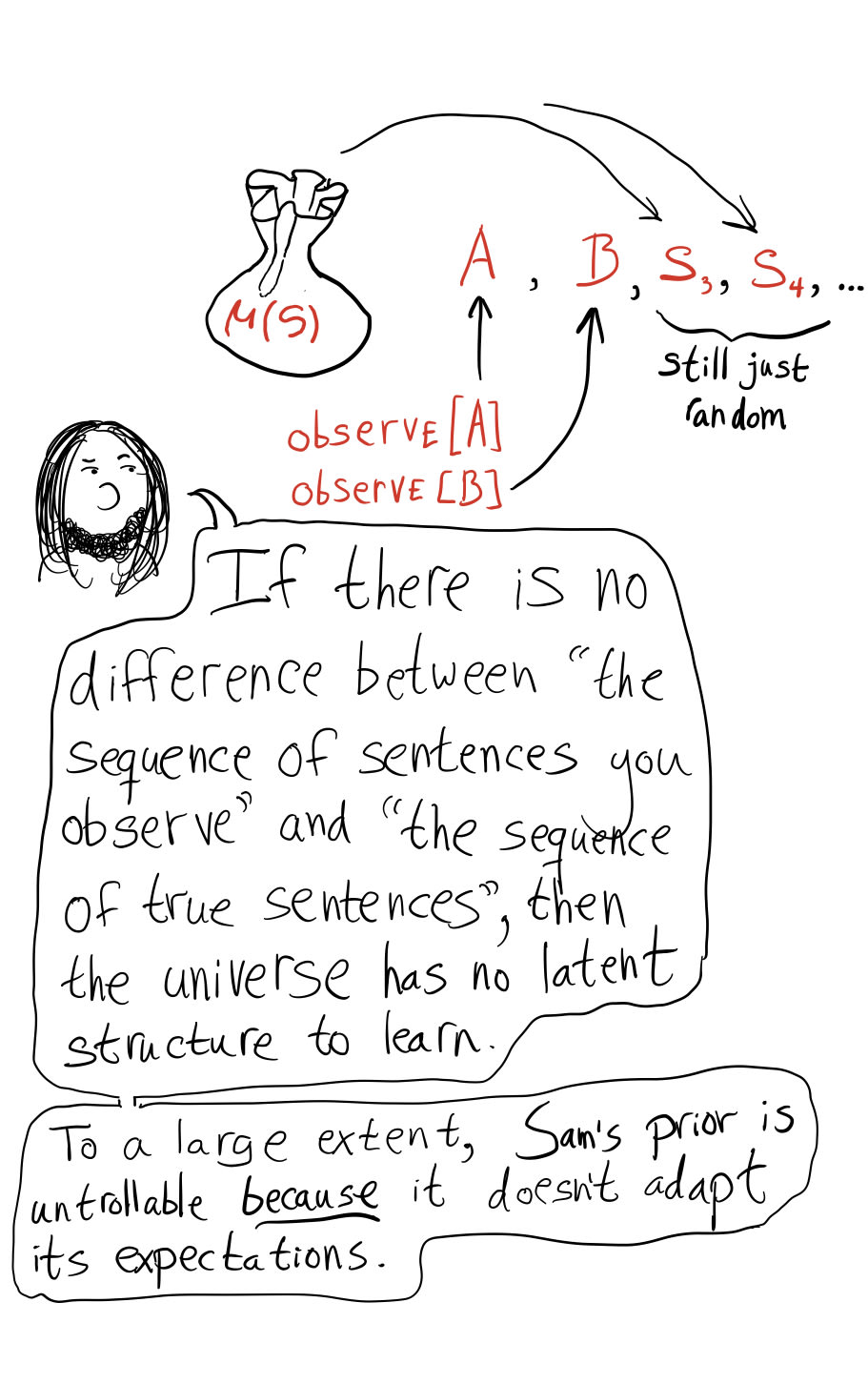
Suppose nature is showing you true sentences one at a time. Model them as drawn randomly from a fixed distribution $μ (S)$ , but enforcing propositional consistency.

Does this mean nature has to in fact be showing me sentences sampled from this fixed distribution, or am I just pretending that that's what it's doing when I update my prior?

Does this work when sentences are shown to me in an adversarial order?

[-]Diffractor7y100

You're pretending that it's what nature is doing what you update your prior. It works when sentences are shown to you in an adversarial order, but there's the weird aspect that this prior expects the sentences to go back to being drawn from some fixed distribution afterwards. It doesn't do a thing where it goes "ah, I'm seeing a bunch of blue blocks selectively revealed, even though I think there's a bunch of red blocks, the next block I'll have revealed will probably be blue". Instead, it just sticks with its prior on red and blue blocks.