But if you throw out causality along with time, it is hard to see how a low-entropy terminal condition and high-entropy initial condition could produce the same pattern of similar and dissimilar regions.
Aren't you assuming an expanding universe here? Some physicists speculate that if the universe were to contract in a Big Crunch, quantum decoherence would reverse and macroscopic entropy would decrease as highly correlated quantum fluctuations would be erased by destructive interference. The end effect is that the thermodynamic arrow of time is reversed and such a situation becomes indistinguishable from an expanding universe with increasing entropy. I'm not sure if this is a widely accepted view.
"It still seems to me that there is some actual connection that makes it more likely for me to wake up tomorrow as Eliezer Yudkowsky, than as Britney Spears."
Connection between what and what? If there is no time, there are no separate moments or instants to be connected to each other. There is just a thing, you, existing. And not even existing continuously, just existing (outside of time).
And yet fire as a phenomenon exists in several spatio-temporal coordinates, right? If the observer of consciousness is a property of conscious experience as a physical phenomena, maybe we should expect to find it wherever consciousness exists.
Your comfort with expressing uncertainty, including rather high levels of fundamental uncertainty, is improving your thinking and your writing, in my opinion.
I am uncertain about difficult problems, HA. I refuse to fake modesty on problems that are easy unto me. Even though I know some people find uncertainty reassuring, I will not pretend to be uncertain on straightforward problems; the truly wise would not be impressed. You should realize that being uncertain about a problem yourself, does not mean that uncertainty is the inherently correct attitude.
I refuse to fake modesty on problems that are easy unto me.And how have you confirmed that you've produced the correct answers for the problems that are "easy unto you", especially when the issue is one that is generally recognized as uncertain or unknown?
It's not a matter of modesty so much as skepticism.
If the universe is timeless, but causal, it is an interesting empirical observation that causal direction never seems to contradict 'temporal direction.'
I don't want to speak for Pearl, but my understanding of his position is that causality is more fundamental than probability in the human mind (not necessarily more fundamental in reality).
Wait a second, this doesn't make sense. If the universe is timeless, then you don't have to actually simulate the universe on a computer. You can just create a detailed model of the universe, put in the neccesery causality structure, stick it in the RAM, and voila! you have conscious beings living out their lives in a universe. You don't even have to put it in the RAM, you can just write out symbols on a piece of paper! Or can this impeccable line of reasoning be invalidated by experimental evidence?
18 months too late, but http://xkcd.com/505/
By Eliezer's line of reasoning above - that the subjective experience is in the causal change between one state and the 'next' then yes, symbols are as good a substrate as any. FWIW, this is how I see things too.
4 years too late but... this is missing the point of both Eliezer and IL. Eliezer/Barbour's timeless physics has no changing state over time, because there is no time. Both states exist in a timeless configuration space, and the causal connection between them is only inferred. IL is trying to illustrate this leads to some pretty rediculous conclusions - such as that all you have to do is write down the states on a piece of paper, and then viola - you have created conscious beings even though no computation is actually going on.
EDIT: For what it's worth I think the Barbour's physics is a mysterious answer that doesn't actually dissolve any of the questions it purports to solve..
"I am uncertain about difficult problems, HA. I refuse to fake modesty on problems that are easy unto me. Even though I know some people find uncertainty reassuring, I will not pretend to be uncertain on straightforward problems; the truly wise would not be impressed. You should realize that being uncertain about a problem yourself, does not mean that uncertainty is the inherently correct attitude."
This response is a result of a fair and reasonable reading of my comment?
Don't think that any of this preserves time, though, or distinguishes the past from the future. I am just holding onto cause and effect and computation and even anticipation for a little while longer.
What is the difference between a time-like relationship and a causal relationship? How have you not preserved time by preserving causality?
What is the difference between a time-like relationship and a causal relationship?Easy: time-like relationships do not imply causality. Just because something follows another thing in sequence - a time-like relationship - does not mean that something implies the other things - a causal relationship.
Post hoc ergo propter hoc....
HA, that's what you get for paying compliments around here!
IL, think of it like this. If you simulated a conscious being one moment-slice at a time, presumably you'd think of it as 'conscious'. So if you simulate all those moment-slices at once, why would it be any less conscious? Whatever the detail, we are reasonably certain that The Passage Of Time is not a fundamental element of the universe, but rather the way we seem to experience things.
Has anyone else read Vonnegut's Slaughterhouse-5? Great plotline about alien beings who experience all of their lives simultaneously.
But if you throw out causality along with time, it is hard to see how a low-entropy terminal condition and high-entropy initial condition could produce the same pattern of similar and dissimilar regions.
My intuition differs - but for those who think otherwise this would be well worth trying to show the difference more formally.
Isn't causality strictly a map of a world strictly governed by physical laws? If a billiard ball strikes another ball, causing it to move, that is just our way of describing the motions of the balls. And besides, the universe doesn't even split the world up into individual "objects" or "events," so how can causality really exist?
By the way, any physical system is defined not just by its positions, but by its derivatives and second derivatives as well (I believe this is enough to describe the complete state of a system?). So when you talk about frozen states in a timeless universe, they still have to have time derivatives (in our perception of them). In other words, a sequence of still claymation frames and continuous motion may produce the same movie, but they correspond to very different realities.
Isn't causality strictly a map of a world strictly governed by physical laws? If a billiard ball strikes another ball, causing it to move, that is just our way of describing the motions of the balls. And besides, the universe doesn't even split the world up into individual "objects" or "events," so how can causality really exist?
By the way, any physical system is defined not just by its positions, but by its derivatives and second derivatives as well (I believe this is enough to describe the complete state of a system?). So when you talk about frozen states in a timeless universe, they still have to have time derivatives (in our perception of them). In other words, a sequence of still claymation frames and continuous motion may produce the same movie, but they correspond to very different realities.
Now my mind is blown. Great post, and great response to HA.
There is an old saying: "Correlation does not imply causation." I don't know if this is my own thought, or something I remember hearing, but on seeing this saying, a phrase ran through my mind: If correlation does not imply causation, what does?
"Imply" here means "imply with certainty", making the saying good advice for people who don't understand probability.
It still seems to me that there is some actual connection that makes it more likely for me to wake up tomorrow as Eliezer Yudkowsky, than as Britney Spears.
This, at least, is naive - what is the "me" that is more likely to wake up as EY? If "you" woke up as Britney Spears, "you" would be Britney Spears, with her memories and everything. I'd be very surprised if this sentence proved to mean anything, even if a long-term connected picture is necessary for anticipation. (Incidentally, an intermediate view is possible, where experience-moments supervene on short-but-nonzero-duration causal structures - in order to evade Dust Theory - but nothing (except memory) links the experience-moments.)
IL, to do what you suggest you'd have to actually compute the history of your universe, meaning the causal relations would exist, so there wouldn't be any problem with there being consciousness.
Now my mind is blown. Great post, and great response to HA.
There is an old saying: "Correlation does not imply causation." I don't know if this is my own thought, or something I remember hearing, but on seeing this saying, a phrase ran through my mind: If correlation does not imply causation, what does?
"Imply" here means "imply with certainty", making the saying good advice for people who don't understand probability.
It still seems to me that there is some actual connection that makes it more likely for me to wake up tomorrow as Eliezer Yudkowsky, than as Britney Spears.
This, at least, is naive - what is the "me" that is more likely to wake up as EY? If "you" woke up as Britney Spears, "you" would be Britney Spears, with her memories and everything. I'd be very surprised if this sentence proved to mean anything, even if a long-term connected picture is necessary for anticipation. (Incidentally, an intermediate view is possible, where experience-moments supervene on short-but-nonzero-duration causal structures - in order to evade Dust Theory - but nothing (except memory) links the experience-moments.)
IL, to do what you suggest you'd have to actually compute the history of your universe, meaning the causal relations would exist, so there wouldn't be any problem with there being consciousness.
Now my mind is blown. Great post, and great response to HA.
There is an old saying: "Correlation does not imply causation." I don't know if this is my own thought, or something I remember hearing, but on seeing this saying, a phrase ran through my mind: If correlation does not imply causation, what does?
"Imply" here means "imply with certainty", making the saying good advice for people who don't understand probability.
It still seems to me that there is some actual connection that makes it more likely for me to wake up tomorrow as Eliezer Yudkowsky, than as Britney Spears.
This, at least, is naive - what is the "me" that is more likely to wake up as EY? If "you" woke up as Britney Spears, "you" would be Britney Spears, with her memories and everything. I'd be very surprised if this sentence proved to mean anything, even if a connected picture is necessary for anticipation. (I'm drawn to an intermediate view, where experience-moments supervene on short-but-nonzero-duration causal structures - in order to evade Dust Theory - but nothing (except memory) links the experience-moments.)
IL, to do what you suggest you'd have to actually compute the history of your universe, meaning the causal relations would exist, so there wouldn't be any problem with there being consciousness.
Caledonian: thanks for the reply, but that wasn't what I was getting at. I can see that things in a temporal sequence may not be causally related - e.g. the light flashes and then the bell rings, but the light didn't cause the bell. My question was about the reverse implication: if causality exists, such that A causes B, does that not necessarily imply that A preceded B and that time exists? If not, what aspect of time is not included within the notion of causality such that we can have causality but not time?
The only case I can think of offhand would be a time loop: grampa tells dad a secret, dad tells it to me, then I go back in time and tell it to grampa. In this case causality and time diverge for at least part of the loop. But in Elizier's explanation of causality without time, where you use Bayesian analysis to determine which events in a series caused the others, requires that there be no causality loops. So I don't think my time loop example answers my question: what is the difference between causality-with-time and causality-without-time?
Nick: IL, to do what you suggest you'd have to actually compute the history of your universe, meaning the causal relations would exist, so there wouldn't be any problem with there being consciousness.
I don't think that's correct. You could populate your model with random data, and if that data happens to be an accurate representation of the timeless universe, then poof you have created consciousness with no computation required (unless you believe that acquiring random data and writing it to RAM is "computation" of the kind that should create causality and consciousness).
Granted, most such randomly populated models wouldn't contain causality or consciousness. But a non-zero number of them would.
I think IL's point stands. If the universe is timeless, then a sufficiently large integer is full of conscious beings.
No, because there are no causal relationships, or relationships at all, within the randomly generated memory. If all you know is the prior distribution, not that the large-scale structure is in fact meaningful, there's no mutual information between any of the bits; and even once you know all the bits, since they're independent and random you can't say "this bit is 1 because this bit is 0."
This all smells of Mind Projection Fallacy, now that I think about it.
if causality exists, such that A causes B, does that not necessarily imply that A preceded BShort answer: no. Causality loops are logically possible, although it's not known whether our universe's physics permit them. B could precede A and still be caused by it - and either A or B could be its own cause and its own effect.
and that time exists?I think you would need to be clearer about what you meant by 'time' and 'exist'. A conceptual model of potential relationships between states might be useful, and that could be what you mean by saying they are linked by time. As for existence, I'm not sure that time meets the criteria for us to be able to say it does or does not exist. What color is an electron? How salty are quadratics? The concepts do not apply.
What is there to support the assumption that the universe generates future values independently of each other?
I feel agreement with "I would sooner associate consciousness with the change in a brain than with the brain itself, if I had to pick one or the other.", and yet I wonder. Doesn't a configuration space contain the fact that change is occurring, at least in the sense that it contains the informational content of relative velocities, not just of relative positions? Also, I have long asserted that experience associated with static configurations seems to me to be close to isomorphic to experience associated with multiple instantiations of a computation. In any event, even if we have retained causality we have still eliminated change.
Very good points Nick T!
Michael: could you elaborate on "Also, I have long asserted that experience associated with static configurations seems to me to be close to isomorphic to experience associated with multiple instantiations of a computation."?
Ricky: I don't think that assumption is being made; rather, you have to transform causal hypotheses with intramoment dependencies into ones without (this seems like it should always be possible).
Eliezer: this may indicate I missed the point of that section, but you can generate a high→low entropy history by computing a low→high entropy history and reversing the frames. It looks to me like Bayesian causality naturally accompanies increase in entropy, since (very handwavingly, this is hard for me to verbalize) P(M2|R1,R2) ≠ P(M2|M1,R1,R2) is more likely to hold if R has higher entropy than M. (Is there a different standard term?)
This definition of causality doesn't seem to work, since the universe clearly doesn't generate future values independently of each other. Consider the following story:
On Monday I decide to buy 2 windows of the same mass. Suppose I want to buy the biggest windows I can afford, and I have money in two bank accounts that I can use for this purpose. On Tuesday a couple of cute little vandals break both of my windows. Some of the glass falls inside my home, and rest outside. Now let:
L1 = how much money I had in bank 1 L2 = how much money I had in bank 2 M1 = mass of window 1 M2 = mass of window 2 R1 = mass of glass that fell inside my home R2 = mass of glass that fell outside my home
Intuitively it seems pretty obvious that the arrow of causality runs from left to right, but if you use the definition Eliezer gave, you'd get the opposite result. Quoting Eliezer:
if we see:
P(M2|L1,L2) ≠ P(M2|M1,L1,L2) P(M2|R1,R2) = P(M2|M1,R1,R2)
Then we can guess causality is flowing from right to left.
Well, P(M2|L1,L2) ≠ P(M2|M1,L1,L2) because M2 depends on the price of glass as well as L1 and L2, but knowing M1 gives us the precise value of M2 (remember that I wanted to buy 2 windows of the same mass). P(M2|R1,R2) = P(M2|M1,R1,R2) since M2=(R1+R2)/2 and M1 doesn't give any more information on top of that.
Nick: What is there to support the assumption that causal hypotheses with intramoment dependencies can always be transformed into ones without?
Dynamically Linked, that's cheating because M1 always equals M2. It's like those division by zero proofs.
Regardless, Eliezer's point here is utterly beautiful and blew my mind, but I just want to check it's applicability in practice:
Suppose that we do know L1 and L2, but we do not know R1 and R2. Will learning M1 tell us anything about M2?
That is, will we observe the conditional dependence
P(M2|L1,L2) ≠ P(M2|M1,L1,L2)
to hold? The answer, on the assumption that causality flows to the right, and on the other assumptions previously given, is no.
True if we're sure we're perfectly reading L1/L2 and perfectly interpreting them to predict M2. But if not then I think the answer's yes because M1 provides additional implicit evidence about L1/L2 than we get from an imperfect reading or interpretation of L1/L2 alone.
Then again, you still get evidence about the direction of causality by how much P(M2|L1,L2) and P(M2|M1,L1,L2) tend to approximately equality in each direction, so even very imperfect knowledge could be got around with statistical analysis. I haven't read Judea Pearl's book yet so sorry if I this is naive or already discussed.
RI, what if I wanted to buy two windows such that one is twice the mass of the other. Is that still cheating?
Nick, how would you transform my causal hypothesis (in the comment above) with intramoment dependencies into one without?
Caledonian: What I mean by "time" is whatever Eliezer means by it, and what I mean by "exist" is that thing that Eliezer says causality does but time doesn't. It seems to me that time and causality are so intertwined that they are surely the same thing; if you have causality but not time, then I don't understand what this "time" thing is that you don't have.
When Eliezer says things like "Our equations don't need a t in them, so we can banish the t and make our ontology that much simpler", perhaps I need a better understanding of exactly what he's proposing to banish.
Perhaps my first clue is your point that causality loops are logically possible. Perhaps time loops aren't logically possible, and that's one way in which the two are not the same. Perhaps I'm using a different mental dictionary than everyone else in these threads.
I'm not sure that the "arrows" are more real in all cases.
Well, first, as far as bijective deterministic thing, I'm going to say that there is no prefered direction, no "true" internal causality direction, given that the rule in all candidate directions is equally simple in either direction and equally local. In that case, claiming any arrows would seem to be epiphenomenal. I mean, it looks like the only thing it could mean there is if something external to the system violated its fundamental rules, reaching in and altering the system somewhere. Then the direction in which the change would propagate would be the causality direction. But then, that just brings in a larger external system and one can ask about the total causality of that...
Perhaps from there we ought take the idea that a simple discrete unique direction of causality is simply a fundamentally wrong model?
Now, if you have some deterministic system which is not bijective, then it does seem pretty clear that the direction in which it's deterministic would perhaps the the most objectively valid direction for "objective causality"
A refinement: Bijective and local, but if we consider a step in some direction, A -> B, such that to determine the state of a neighborhood in B of size x, you need a neighborhood in A of size y, but if going in the B -> A direction, to determine state of neighborhood of size x in A you need neighborhood of size z > y in B, then I think I'd say A -> B is the "natural" direction of causality.
Frankly, I'm semi suspecting that perhaps the concepts of locality and causality are deeply tied to one another.
Anyways, let's consider Barbour's universe for a moment... What would we consider ultimate cause and effect? The basic rule for the amplitude field + boundry conditions = ultimate cause of everything going on, right?
Perhaps we mean "given that, and given some other thing, but changing some other thing, what happens?"
It looks like perhaps some notion of "relative causality" or "conditional causality" may be in order, rather than simply being tied to a single absolute causality.
Sorry some of this is vague, I'm still thinking it through.
Oh... With Barbour's Platonia, there actually would be something that fits with some of the above: The whole thing about neighborhood size. I THINK the direction away from the origin may be the prefered direction based on that criteria, at least if one starts with a neighborhood as "wide" as it needs to be to hit the boundries.
On the other hand, what if someone started midPlatonia with a hyperspherical shell shaped neighborhood of known values? Then away from the origin of that would be the locally prefered direction... until one hit the boundries. Then stuff would start getting odd.
As I said, I'm still thinking it through, but it does look like some form of notion of relative of conditional causality is really needed.
Consider our brain states... Given that and the physics, there's presumably a natural "forward" direction, or group of prefered directions. (There can't be a single prefered direction in Platonia anyways... I mean, you've got effective branching into the decoherent worlds and all that...)
Now, given some locally prefered direction, we might ask if we held fixed the "tag"/dimensions representing us, but varied some other factors/dimensions that we're curios about, then peek ahead in whatever the "obvious relative to us" prefered directions are for each of the states we're testing, what would be different in each? That would tell us something about what the changing thing causally affects, relative to us.
Sorry this is a bit rambling. I'm confused on this issue too, I'm just here poking and prodding at it and hoping I get out some useful insight.
Noether's theorem links symmetry to conservation laws. If you have an asymmetry in your causality, then you don't have conservation of energy anymore.
An exemple of such a system is Conway's game of Life, where you cannot always deduce the past state of the board from its future state. The sum total of all cells values in a Life board isn't constant over different time slices either, so no conservation there.
Is it possible that on that one you're still attached to one of those comfortable fuzzy thoughts ? Is there for instance a(n emotional) reason to value an universe in which there is causality over one where there isn't ?
The symmetry corresponding to conservation of energy is time translation, not time reversal. That said, I have other reasons to be doubtful of Yudkowsky's thesis here. In particular, I think it really does come down to entropy.
Infotropism: There may be some other things which are conserved in Life, some abstract properties maybe. I dunno, anyone here know? Anyways, does Noether's theorem even apply to it? I thought it just applied to things that had lagrangians or something analogous. Can Life be represented in any mathematical form that ends up with sufficient lagrangian or whatever structure that Noether's theorem can even begin to talk about it?
Also, I think Eliezer was hinting at that possibility, he was partly suggesting something along the lines of "am sticking with this notion until I have something better and less confusing to replace it with."
Since patterns in Conway's Game can grow exponentially and without limit, I doubt there are any useful conservation principles that hold in all cases. There are probably specific pattern sets that obey conservation of certain properties, but not the ruleset as a whole.
I'm not sure what you mean by "grow exponentially" here - they certainly can't add dimension or number of live cells exponentially with respect to time; dimension is only ever added one cell per time-slice and is thus O(n) while number of cells contained within the maximum dimensions is O(n^2) and thus so is the number of live cells.
Nick: Casually, either experience is a property of the math, in which case it only comes from a single instance of a computation (or even from zero instances) or it's a property of the existence of the physical state, in which case it comes from multiple instances, but equally much from one instance that endures for as long as those multiple instances do. Timeless physics may make a third path possible, and there may be other work-arounds, but those two possibilities seem to be the default.
Caledonian: It doesn't need to be a simple sum. What I meant was maybe something a bit more abstract. Perhaps something with some form of "directionality", analogous to momentum, such that different sections can cancel out.
Or maybe some more abstract property, perhaps some completely non local property that turns out to be conserved. Again, I'm not saying there is such a property in Life, merely that it's not obvious to me that there isn't, and that as far as I know, Noether's theorem doesn't apply to this sort of system.
(If I'm wrong about the last, well, someone lemme know? :))
Nick, here's what Judea Pearl wrote on this topic. On page 59 of his book:
This suggests that the consistent agreement between physical and statistical times [i.e., the direction of time and the direction of causality] is a byproduct of the human choice of linguistic primitives and not a feature of physical reality. ... Pearl and Verma (1991) speculated that this preference represents survival pressure to facilitate prediction of future events, and that evolution has evidently ranked this facility more urgent than that of finding hindsighted explanation for current events.
Eliezer wants to go from timeless physics to causality, to computation, to anticipation. He admits being unsure about the latter two steps, but even the first step doesn't seem to work. And besides, timeless physics (and relational physics, which timeless physics builds on top of) itself is highly speculative and problematic. Is the intention to actually convince us of the correctness of these ideas, or just to make us "think outside the box" and realize that these possibilities exist?
I don't see the point in all this.
We have this mathematical Platonia object and the relation across the time dimension is not symmetric: in what we call increasing values of time slices of the Platonia get larger. If you want to talk about some of the structures in the Platonia as "timeless causation" or "computation" then, sure, I have no problem with that. But I don't see that you've created or rescued anything, you've just defined existing words in terms of the Platonia's structure.
I certainly don't see why you are being "forced to grind up reality into disconnected configurations". Why not continuous time? Then you don't need "glue between them" as there is no between. Speaking of which, your example is in discrete time, but does it hold in continuous time? From mathematical finance I've learnt that many counter intuitive things can happen in continuous time stochastic processes. Unfortunately, I'm only just coming to terms with discrete time martingale theory and haven't yet progressed to the continuous case - so I can't answer this question myself.
Yes, the discrete vs. continuous time issue calls into question the conclusions drawn from the example. This is related to my question above: "What is there to support the assumption that the universe generates future values independently of each other?"
Configuration vs computation: Storing a configuration depends on the representation. To say that you're storing a configuration of Conway's Life, rather than some other 2d cellular automaton, requires some commitment that this is the intended computation. I have no idea what such a commitment would look like. Actually doing the computation sounds pretty good, but otherwise?
There is no t coordinate, and no global now sweeping across the universe. Events do not happen in the past or the present or the future, they just are. But there may be a certain... asymmetric locality of relatedness... that preserves "cause" and "effect", and with it, "therefore"
Not to trivialize this, but Phillip Fry helps me think about it, by going back in time and being his own grandfather:
http://en.wikipedia.org/wiki/Roswell_That_Ends_Well
for him, whether he was prior to his father is an unanswerable question, but the story is causally consistent.
I'm not sure I understand, but are you saying there's a reason to view a progression of configurations in one direction over another? I'd always (or at least for a long time) essentially considered time a series of states (I believe I once defined passage of time as a measurement of change), basically like a more complicated version of, say, the graph of y=ln(x). Inverting the x-axis (taking the mirror image of the graph) would basically give you the same series of points in reverse, but all the basic rules would be maintained - the height above the x-axis would always be the natural log of the x-value. Similarly, inverting the progression of configurations would maintain all physical laws. This seems to me fit all your posts on time up until this one.
This one, though, differs. Are you claiming in this post that one could invert the t-axis (or invert the progression of configurations in the timeless view) and obtain different physical laws (or at least violations of the ones in our given progression)? If so, I see a reason to consider a certain order to things. Otherwise, it seems that, while we can say y=ln(x) is "increasing" or describe a derivative at a point, we're merely describing how the points relate to each other if we order them in increasing x-values, rather than claiming that the value of ln(5) depends somehow on the value of ln(4.98) as opposed to both merely depending on the definition of the function. We can use derivatives to determine the temporally local configurations just as we can use derivatives to approximate x-local function values, but as far as I can tell it is, in the end, a configuration A that happens to define brains that contain some information on another configuration B that defined brains that contained information on some configuration C, so we say C happened, then B, then A, just like in the analogy we have a set of points that has no inherent order so we read it in order of increasing x-values (which we generally place left-to-right) but it's not inherently that - it's just a set of y-values that depend on their respective x-values.
Short version: Are you saying there's a physical reason to order the configurations C->B->A other than that A contains memories of B containing memories of C?
I've read this again (along with the rest of the Sequence up to it) and I think I have a better understanding of what it's claiming. Inverting the axis of causality would require inverting the probabilities, such that an egg reforming is more likely than an egg breaking. It would also imply that our brains contain information on the 'future' and none on the 'past', meaning all our anticipations are about what led to the current state, not where the current state will lead.
All of this is internally consistent, but I see no reason to believe it gives us a "real" direction of causality. As far as I can tell, it just tells us that the direction we calculate our probabilities is the direction we don't know.
Going from a low-entropy universe to a high-entropy universe seems more natural, but only because we calculate our probabilities in the direction of low-to-high entropy. If we based our probabilities on the same evidence perceived the opposite direction, it would be low-to-high that seemed to need universes discarded and high-to-low that seemed natural.
...right?
All of this is internally consistent, but I see no reason to believe it gives us a "real" direction of causality.
What do you want out of a "real" direction of causality, other than the above?
Well, Eliezer seems to be claiming in this article that the low-to-high is more valid than the high-to-low, but I don't see how they're anything but both internally consistent
Inverting the axis of causality would require inverting the probabilities, such that an egg reforming is more likely than an egg breaking.
I don't think this is a coherent notion. If we "invert the probabilities" in some literal sense, then yes, the egg reforming is more likely than the egg breaking, but still more likely is the egg turning into an elephant.
Hm. This is true. Perhaps it would be better to say "Perceiving states in opposite-to-conventional order would give us reason to assume probabilities entirely consistent with considering a causality in opposite-to-conventional order."
Unless I'm missing something, the only reason to believe causality goes in the order that places our memory-direction before our non-memory direction is that we base our probabilities on our memory.
Do you know that it doesn't work if we use a deterministic rule, or have you just not tried? Cause I'm trying right now.
"To compute a consistent universe with a low-entropy terminal condition and high-entropy initial condition, you have to simulate lots and lots of universes, then throw away all but a tiny fraction of them that end up with low entropy at the end. With a low-entropy initial condition, you can compute it out locally, without any global checks. So I am not yet ready to throw out the arrowheads on my arrows."
Here's the problem with this argument. Your simulations are occurring as a sub-history of a universe where the second law of thermodynamics already holds. A simulation of a universe with increasing entropy will be a sub-history where entropy increases, and will therefore be more likely to occur than a simulation of a universe with decreasing entropy (i.e. a subhistory where entropy decreases.)
That is, unless your simulation finds a way to dump entropy into the environment. The usual way to do this is by erasing information cf: http://en.wikipedia.org/wiki/Von_Neumann-Landauer_limit . Throwing out the simulations where entropy increased would be one example. Likewise, simulating non-information preserving rules (e.g. Conway's game of life) will also allow entropy to decrease within the simulation -- for example, most random fields of a reasonably small size will settle into a pattern of stable oscillators. This can happen because it is perfectly possible for two ancestor states to go to the same descendent state within the rules of Conway's game, and when this happens, entropy must leak into the environment according to the second law.
If the idea that time stems from the second law is true, and we apply the principle of eliminating variables that are redundant because they don't make any difference, we can collapse the notions of time and entropy into one thing. Under these assummptions, in a universe where entropy is decreasing (relative to our external notion of 'time'), the internal 'time' is in fact running backward.
As also noted by some other commenters, it seems to me that the expressed conditional dependence of different points in a universe is in some way equivalent to increasing entropy.
Let's assume that the laws of the universe described by the LMR picture are in fact time-symmetric and that the number of states each point can be in is too large to describe exactly (i.e. just as is the case in our actual universe, as far as we know). In that case, we can only describe our conditional knowledge of M2 given the states of M1 and R1,2 using very rough descriptions, not using the fully detailed descriptions describing the exact states. It seems to me that this can only be usefully done if there is some kind of structure in the states of M1,2 (a.k.a. low entropy) that matches our coarse description. Saying that the L or M part of the universe is in a low entropy state is equivalent to saying that some of the possible states are much more common for the nodes in the L or M part than other states. Our coarse predictor will necessarily make wrong predictions given some input states. Since the actual laws are time symmetric, if the input states to our predictor were randomly distributed over all possible states, our predictions would fail equally often predicting from left to right or from right to left. Only if on the left the states we can predict correctly happen more often than on the right will there be an inequality in the number of correct predictions.
...except that I now seem to have concluded that time always flows in the opposite direction of what Eliezers conditional dependence indicates, so I'm not sure how to interpret that. Maybe it is because I am assuming time symmetric laws and Eliezer is using time-asymmetric probablistic laws. However, it still seems correct to me that in the case of time symmetric underlying laws and a coarse (incomplete) predictor, predictions can only be better in one way than the other if there is a difference in how often we see correctly predicted input relative to incorrectly predicted input, and therefore if there is a difference in entropy.
Okay so the tldr; of this could be : In a nondeterministic universe, effects imply at least one cause, but a cause does not imply an effect, therefore a causal model implies some kind of time like asymmetry. Correct?
So then it seems to me you can make the obvious extension into a quantum universe by subsituting probability mass for amplitudes. So that in our quantum, deterministic universe, the asymmetry comes from the way amplitude spreads down everett branches, and our confinement to a single one. A dead cat in schroedinger's box now implies a live one a certain time in the past, a live one now does not necessitate a dead one at any given time in the past.
I am aware of the standard argument that anything resembling an "arrow of time" should be made to stem strictly from the second law of thermodynamics and the low-entropy initial condition. But if you throw out causality along with time, it is hard to see how a low-entropy terminal condition and high-entropy initial condition could produce the same pattern of similar and dissimilar regions.
I don't completely understand your argument, but note that computing the universe from a low-entropy initial condition might require fewer bits to specify, so something like the universal distribution would give it higher weight. So if the mathematical multiverse assigns observations to observers using a simplicity-based distribution, that might explain why we're not in an ordered bubble about to be eaten by chaos or something...
well, for me is still an enigma how statistical series, any statistical series, wich is by definition defined as pairs of time|numbers series can be in any logical way ... timeless
you have that string of naked numbers, pure numbers ... and its timecoded by its very pure defined nature! 1rst value, second value, third value etcaetera ... that is already time coded and that can't be changed unless you are alowed to work with statistical series where you can randomly permute series members and still pretend that it is still statistical series .. and that, i think, will defeat any statistical analisis of anything because you will work with nothing more than pure and random numerical garbage if you are serios and use real randomness ;-p
so for me timeless causality is just another logical and random pure garbage and nonsense
I would sooner associate experience with the arrows than the nodes, if I had to pick one or the other! I would sooner associate consciousness with the change in a brain than with the brain itself, if I had to pick one or the other.
This also lets me keep, for at least a little while longer, the concept of a conscious mind being connected to its future Nows, and anticipating some future experiences rather than others. Perhaps I will have to throw out this idea eventually, because I cannot seem to formulate it consistently; but for now, at least, I still cannot do without the notion of a "conditional probability".
I wrote a long comment, but the main question is: Why do you guess an answer here, instead of "Shut up and calculate"?
Why are/were you favouring the hypothesis? Considering what I have read so far from you, I find it more likely that I have missed something, than there being no reason, but I can't find it....
If you look into the brains of Alpha and Betty in the morning, as well as the weather forecast, the attitude of each girl to the food that their parents will give them today (that is, how much one of them will deteriorate/elevate their mood) and into the brains of their parents (how they will interact with each other and with their daughters) etc., you will have the conditions to understand which of the girls is more likely to throw a stone.
I haven't made my way through your article yet, though I hope to. But I was a little surprised when you discussed how correlation does not prove causation that you did not mention David Hume who basically says, at least in my reading of him, that no matter how many times one observes lightning and thunder you can not say with absolute certainty that lightning causes thunder.
Followup to: Timeless Physics
Julian Barbour believes that each configuration, each individual point in configuration space, corresponds individually to an experienced Now—that each instantaneous time-slice of a brain is the carrier of a subjective experience.
On this point, I take it upon myself to disagree with Barbour.
There is a timeless formulation of causality, known to Bayesians, which may glue configurations together even in a timeless universe. Barbour may not have studied this; it is not widely studied.
Such causal links could be required for "computation" and "consciousness"—whatever those are. If so, we would not be forced to conclude that a single configuration, encoding a brain frozen in time, can be the bearer of an instantaneous experience. We could throw out time, and keep the concept of causal computation.
There is an old saying: "Correlation does not imply causation." I don't know if this is my own thought, or something I remember hearing, but on seeing this saying, a phrase ran through my mind: If correlation does not imply causation, what does?
Suppose I'm at the top of a canyon, near a pile of heavy rocks. I throw a rock over the side, and a few seconds later, I hear a crash. I do this again and again, and it seems that the rock-throw, and the crash, tend to correlate; to occur in the presence of each other. Perhaps the sound of the crash is causing me to throw a rock off the cliff? But no, this seems unlikely, for then an effect would have to precede its cause. It seems more likely that throwing the rock off the cliff is causing the crash. If, on the other hand, someone observed me on the cliff, and saw a flash of light, and then immediately afterward saw me throw a rock off the cliff, they would suspect that flashes of light caused me to throw rocks.
Perhaps correlation, plus time, can suggest a direction of causality?
But we just threw out time.
You see the problem here.
Once, sophisticated statisticians believed this problem was unsolvable. Many thought it was unsolvable even with time. Time-symmetrical laws of physics didn't seem to leave room for asymmetrical causality. And in statistics, nobody thought there was any way to define causality. They could measure correlation, and that was enough. Causality was declared dead, and the famous statistician R. A. Fisher testified that it was impossible to prove that smoking cigarettes actually caused cancer.
Anyway...
Let's say we have a data series, generated by taking snapshots over time of two variables 1 and 2. We have a large amount of data from the series, laid out on a track, but we don't know the direction of time on the track. On each round, the past values of 1 and 2 probabilistically generate the future value of 1, and then separately probabilistically generate the future value of 2. We know this, but we don't know the actual laws. We can try to infer the laws by gathering statistics about which values of 1 and 2 are adjacent to which other values of 1 and 2. But we don't know the global direction of time, yet, so we don't know if our statistic relates the effect to the cause, or the cause to the effect.
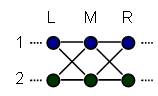
When we look at an arbitrary value-pair and its neighborhood, let's call the three slices L, M, and R for Left, Middle, and Right.
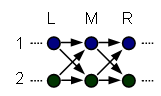
We are considering two hypotheses. First, that causality could be flowing from L to M to R:
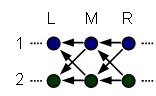
Second, that causality could be flowing from R to M to L:
As good Bayesians, we realize that to distinguish these two hypotheses, we must find some kind of observation that is more likely in one case than in the other. But what might such an observation be?
We can try to look at various slices M, and try to find correlations between the values of M, and the values of L and R. For example, we could find that when M1 is in the + state, that R2 is often also in the + state. But is this because R2 causes M1 to be +, or because M1 causes R2 to be +?
If throwing a rock causes the sound of a crash, then the throw and the crash will tend to occur in each other's presence. But this is also true if the sound of the crash causes me to throw a rock. So observing these correlations does not tell us the direction of causality, unless we already know the direction of time.
From looking at this undirected diagram, we can guess that M1 will correlate to L1, M2 will correlate to R1, R2 will correlate to M2, and so on; and all this will be true because there are lines between the two nodes, regardless of which end of the line we try to draw the arrow upon. You can see the problem with trying to derive causality from correlation!
Could we find that when M1 is +, R2 is always +, but that when R2 is +, M1 is not always +, and say, "M1 must be causing R2"? But this does not follow. We said at the beginning that past values of 1 and 2 were generating future values of 1 and 2 in a probabilistic way; it was nowhere said that we would give preference to laws that made the future deterministic given the past, rather than vice versa. So there is nothing to make us prefer the hypothesis, "A + at M1 always causes R2 to be +" to the hypothesis, "M1 can only be + in cases where its parent R2 is +".
Ordinarily, at this point, I would say: "Now I am about to tell you the answer; so if you want to try to work out the problem on your own, you should do so now." But in this case, some of the greatest statisticians in history did not get it on their own, so if you do not already know the answer, I am not really expecting you to work it out. Maybe if you remember half a hint, but not the whole answer, you could try it on your own. Or if you suspect that your era will support you, you could try it on your own; I have given you a tremendous amount of help by asking exactly the correct question, and telling you that an answer is possible.
...
So! Instead of thinking in terms of observations we could find, and then trying to figure out if they might distinguish asymmetrically between the hypotheses, let us examine a single causal hypothesis and see if it implies any asymmetrical observations.
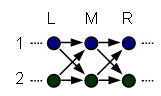
Say the flow of causality is from left to right:
Suppose that we do know L1 and L2, but we do not know R1 and R2. Will learning M1 tell us anything about M2?
That is, will we observe the conditional dependence
to hold? The answer, on the assumption that causality flows to the right, and on the other assumptions previously given, is no. "On each round, the past values of 1 and 2 probabilistically generate the future value of 1, and then separately probabilistically generate the future value of 2." So once we have L1 and L2, they generate M1 independently of how they generate M2.
But if we did know R1 or R2, then, on the assumptions, learning M1 would give us information about M2. Suppose that there are siblings Alpha and Betty, cute little vandals, who throw rocks when their parents are out of town. If the parents are out of town, then either Alpha or Betty might each, independently, decide to throw a rock through my window. If I don't know whether a rock has been thrown through my window, and I know that Alpha didn't throw a rock through my window, that doesn't affect my probability estimate that Betty threw a rock through my window—they decide independently. But if I know my window is broken, and I know Alpha didn't do it, then I can guess Betty is the culprit. So even though Alpha and Betty throw rocks independently of each other, knowing the effect can epistemically entangle my beliefs about the causes.
Similarly, if we didn't know L1 or L2, then M1 should give us information about M2, because from the effect M1 we can infer the state of its causes L1 and L2, and thence the effect of L1/L2 on M2. If I know that Alpha threw a rock, then I can guess that Alpha and Betty's parents are out of town, and that makes it more likely that Betty will throw a rock too.
Which all goes to say that, if causality is flowing from L to M to R, we may indeed expect the conditional dependence
to hold.
So if we observe, statistically, over many time slices:
Then we know causality is flowing from left to right; and conversely if we see:
Then we can guess causality is flowing from right to left.
This trick used the assumption of probabilistic generators. We couldn't have done it if the series had been generated by bijective mappings, i.e., if the future was deterministic given the past and only one possible past was compatible with each future.
So this trick does not directly apply to reading causality off of Barbour's Platonia (which is the name Barbour gives to the timeless mathematical object that is our universe).
However, think about the situation if humanity sent off colonization probes to distant superclusters, and then the accelerating expansion of the universe put the colonies over the cosmological horizon from us. There would then be distant human colonies that could not speak to us again: Correlations in a case where light, going forward, could not reach one colony from another, or reach any common ground.
On the other hand, we would be very surprised to reach a distant supercluster billions of light-years away, and find a spaceship just arriving from the other side of the universe, sent from another independently evolved Earth, which had developed genetically compatible indistinguishable humans who speak English. (A la way too much horrible sci-fi television.) We would not expect such extraordinary similarity of events, in a historical region where a ray of light could not yet have reached there from our Earth, nor a ray of light reached our Earth from there, nor could a ray of light reached both Earths from any mutual region between. On the assumption, that is, that rays of light travel in the direction we call "forward".
When two regions of spacetime are timelike separated, we cannot deduce any direction of causality from similarities between them; they could be similar because one is cause and one is effect, or vice versa. But when two regions of spacetime are spacelike separated, and far enough apart that they have no common causal ancestry assuming one direction of physical causality, but would have common causal ancestry assuming a different direction of physical causality, then similarity between them... is at least highly suggestive.
I am not skilled enough in causality to translate probabilistic theorems into bijective deterministic ones. And by calling certain similarities "surprising" I have secretly imported a probabilistic view; I have made myself uncertain so that I can be surprised.
But Judea Pearl himself believes that the arrows of his graphs are more fundamental than the statistical correlations they produce; he has said so in an essay entitled "Why I Am Only A Half-Bayesian". Pearl thinks that his arrows reflect reality, and hence, that there is more to inference than just raw probability distributions. If Pearl is right, then there is no reason why you could not have directedness in bijective deterministic mappings as well, which would manifest in the same sort of similarity/dissimilarity rules I have just described.
This does not bring back time. There is no t coordinate, and no global now sweeping across the universe. Events do not happen in the past or the present or the future, they just are. But there may be a certain... asymmetric locality of relatedness... that preserves "cause" and "effect", and with it, "therefore". A point in configuration space would never be "past" or "present" or "future", nor would it have a "time" coordinate, but it might be "cause" or "effect" to another point in configuration space.
I am aware of the standard argument that anything resembling an "arrow of time" should be made to stem strictly from the second law of thermodynamics and the low-entropy initial condition. But if you throw out causality along with time, it is hard to see how a low-entropy terminal condition and high-entropy initial condition could produce the same pattern of similar and dissimilar regions. Look at in another way: To compute a consistent universe with a low-entropy terminal condition and high-entropy initial condition, you have to simulate lots and lots of universes, then throw away all but a tiny fraction of them that end up with low entropy at the end. With a low-entropy initial condition, you can compute it out locally, without any global checks. So I am not yet ready to throw out the arrowheads on my arrows.
And, if we have "therefore" back, if we have "cause" and "effect" back—and science would be somewhat forlorn without them—then we can hope to retrieve the concept of "computation". We are not forced to grind up reality into disconnected configurations; there can be glue between them. We can require the amplitude relations between connected volumes of configuration space, to carry out some kind of timeless computation, before we decide that it contains the timeless Now of a conscious mind. We are not forced to associate experience with an isolated point in configuration space—which is a good thing from my perspective, because it doesn't seem to me that a frozen brain with all the particles in fixed positions ought to be having experiences. I would sooner associate experience with the arrows than the nodes, if I had to pick one or the other! I would sooner associate consciousness with the change in a brain than with the brain itself, if I had to pick one or the other.
This also lets me keep, for at least a little while longer, the concept of a conscious mind being connected to its future Nows, and anticipating some future experiences rather than others. Perhaps I will have to throw out this idea eventually, because I cannot seem to formulate it consistently; but for now, at least, I still cannot do without the notion of a "conditional probability". It still seems to me that there is some actual connection that makes it more likely for me to wake up tomorrow as Eliezer Yudkowsky, than as Britney Spears. If I am in the arrows even more than the nodes, that gives me a direction, a timeless flow. This may possibly be naive, but I am sticking with it until I can jump to an alternative that is less confusing than my present confused state of mind.
Don't think that any of this preserves time, though, or distinguishes the past from the future. I am just holding onto cause and effect and computation and even anticipation for a little while longer.
Part of The Quantum Physics Sequence
Next post: "Timeless Identity"
Previous post: "Timeless Beauty"