This is one of three sets of fixed point exercises. The first post in this sequence is here, giving context.
1. (1-D Sperner's lemma) Consider a path built out of edges as shown. Color each vertex blue or green such that the leftmost vertex is blue and the rightmost vertex is green. Show that an odd number of the edges will be bichromatic.

2. (Intermediate value theorem) The Bolzano-Weierstrass theorem states that any bounded sequence in has a convergent subsequence. The intermediate value theorem states that if you have a continuous function such that and , then there exists an such that . Prove the intermediate value theorem. It may be helpful later on if your proof uses 1-D Sperner's lemma and the Bolzano-Weierstrass theorem
3. (1-D Brouwer fixed point theorem) Show that any continuous function has a fixed point (i.e. a point with ). Why is this not true for the open interval ?
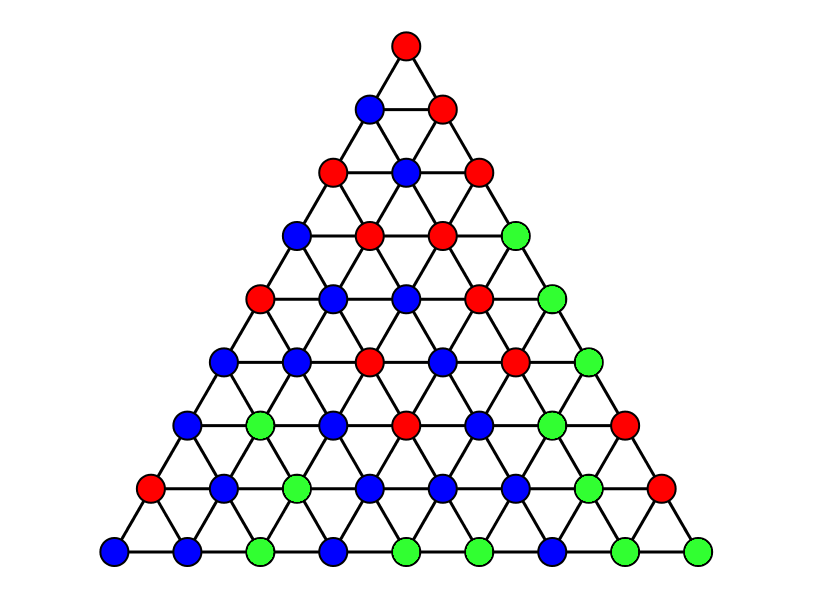
4. (2-D Sperner's lemma) Consider a triangle built out of smaller triangles as shown. Color each vertex red, blue, or green, such that none of the vertices on the large bottom edge are red, none of the vertices on the large left edge are green, and none of the vertices on the large right edge are blue. Show that an odd number of the small triangles will be trichromatic.
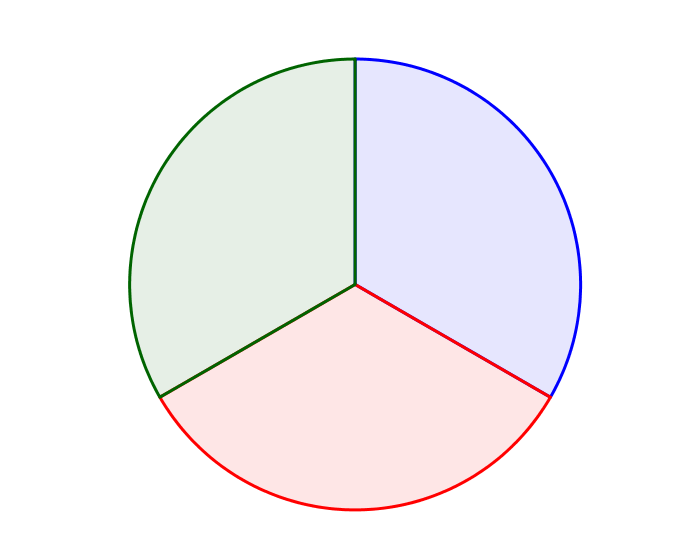
5. Color the all the points in the disk as shown. Let be a continuous function from a closed triangle to the disk, such that the bottom edge is sent to non-red points, the left edge is sent to non-green points, and the right edge is sent to non-blue points. Show that sends some point in the triangle to the center.
6. Show that any continuous function from closed triangle to itself has a fixed point.
7. (2-D Brouwer fixed point theorem) Show that any continuous function from a compact convex subset of to itself has a fixed point. (You may use the fact that given any closed convex subset of , the function from to which projects each point to the nearest point in is well defined and continuous.)
8. Reflect on how non-constructive all of the above fixed-point findings are. Find a parameterized class of functions where for each , , and the function is continuous, but there is no continuous way to pick out a single fixed point from each function (i.e. no continuous function such that is a fixed point of for all ).
9. (Sperner's lemma) Generalize exercises 1 and 4 to an arbitrary dimension simplex.
10. (Brouwer fixed point theorem) Show that any continuous function from a compact convex subset of to itself has a fixed point.
11. Given two nonempty compact subsets , the Hausdorff distance between them is the supremum
over all points in either subset of the distance from that point to the other subset. We call a set valued function a continuous Hausdorff limit if there is a sequence of continuous functions from to whose graphs, , converge to the graph of , , in Hausdorff distance. Show that every continuous Hausdorff limit from a compact convex subset of to itself has a fixed point (a point such that ).
12. Let and be nonempty compact convex subsets of . We say that a set valued function, is a Kakutani function if the graph of , , is closed, and is convex and nonempty for all . For example, we could take and to be the interval , and we could have send each to , map to the whole interval , and map to . Show that every Kakutani function is a continuous Hausdorff limit. (Hint: Start with the case where is a unit cube. Construct by breaking into small cubes of side length . Constuct a smaller cube of side length within each cube. Send each small to the convex hull of the images of all points in the cube with a continuous function, and glue these together with straight lines. Make sure you don't accidentally get extra limit points.)
13. (Kakutani fixed point theorem) Show that every Kakutani function from a compact convex subset of to itself has a fixed point.
Please use the spoilers feature - the symbol '>' followed by '!' followed by space -in your comments to hide all solutions, partial solutions, and other discussions of the math. The comments will be moderated strictly to hide spoilers!
I recommend putting all the object level points in spoilers and leaving metadata outside of the spoilers, like so: "I think I've solved problem #5, here's my solution <spoilers>" or "I'd like help with problem #3, here's what I understand <spoilers>" so that people can choose what to read.