The salt in pasta water fallacy
82johnswentworth
58Steven Byrnes
15AnthonyC
0dr_s
1momom2
18Richard_Kennaway
5JenniferRM
34Shmi
26Charlie Steiner
11noggin-scratcher
23Richard Korzekwa
3Alex_Altair
29cozyfractal
5khafra
19Jan_Kulveit
10ponkaloupe
1SpectrumDT
7DirectedEvolution
10RamblinDash
5localdeity
5Steven Byrnes
4localdeity
4Steven Byrnes
2cubefox
5Going Durden
2RamblinDash
2cubefox
2DirectedEvolution
1antanaclasis
9avancil
1dr_s
1avancil
-1dr_s
5Adam Zerner
3Crazy philosopher
3Review Bot
2Ben
1Noosphere89
1Alex Vermillion
1p
1nem
1whestler
1rotatingpaguro
1MentalGear
1MissouriTiger
1moonlight
1transhumanist_atom_understander
1M. Y. Zuo
1Niclas Kupper
1theflowerpot
2Ben
-8Iknownothing
New Comment
Terminologically, I think it would be useful to name this as a variant of the epsilon fallacy, which has the benefit of being exactly what it sounds like.
Also, great post, I love the pasta-cooking analysis.
Another reason the pasta terminology is bad is that I bet a reasonable fraction of the population have always believed that the salt is for taste, and have never heard any other justification. For them, “salt in pasta water fallacy” would be a pretty confusing term. I like “epsilon fallacy”.
I had never heard about the salt making pasta cook faster. I know that some people only add salt when the water is on the point of boiling because this makes the boiling faster (which is also true but a negligibly tiny effect: adding salt before just increases the boiling point, meanwhile adding it when the past is already about to boil breaks surface tension and adds nucleation centres which precipitate the formation of bubbles).
I read the epsilon fallacy and verified that it was good. Then I went to the fallacy tag, opened the list of all the articles with that tag, found the "epsilon" article, and upvoted the tag association itself! That small action was enough to make your old article show up on the first page, and rank just above the genetic fallacy. Hopefully this small action is very effective and making the (apparently best?) name for this issue more salient, for more people, as time progresses :-)
1Seems like it's related to the Motte-and-Bailey fallacy, where people claim more than they can defend, retreat to the defensible claim when pushed, and expand back to the indefensible claim the moment the pressure lets up.
Adding salt makes the pasta taste better. So I think this is a halo effect or manichean error - since salting the water is a good idea, it should do other good things too.
Or just a post-hoc rationalisation, by people who know you're "supposed" to salt the pasta water, but don't really know why. Because they've been taught to cook by example rather than from theory and first principles (as most of us are), maybe by someone who also didn't know why they do it.
If they've also separately heard that salt raises the boiling point of water, but don't really know the magnitude of that effect, then that presents itself as an available salient fact to slot into the empty space in "I salt my pasta water because..."
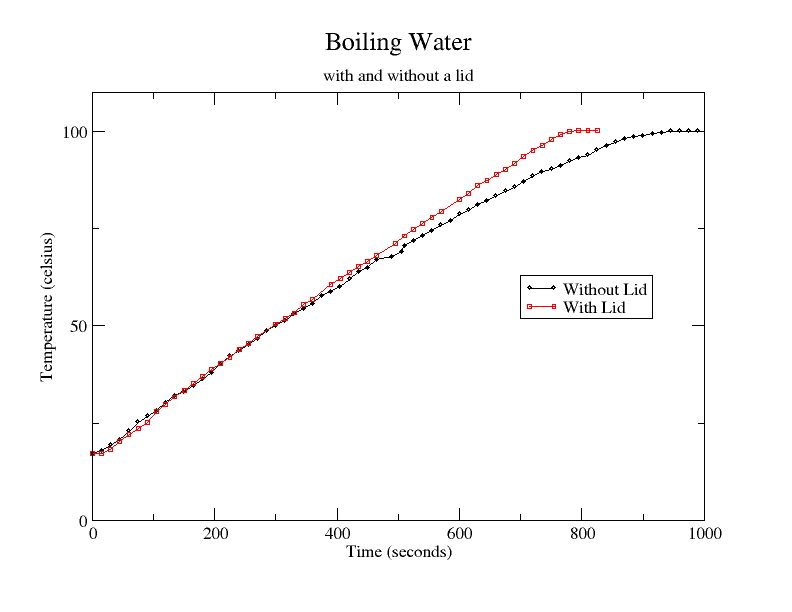
I put a lid on the pot because it saves energy/cooks faster. Or maybe it doesn't, I don't know, I never checked.
I checked and it does work.
It's the horizontal difference that matters and not the vertical one, so the water boils about 200s earlier or 20% faster (according to this one experiment) which quite nice!
Note also that there are several free parameters in this example. E.g., I just moved to Germany, and now have wimpy German burners on my stove. If I put on a large container with 6L or more of water, and I do not cover it, the water will never go beyond bubble formation into a light simmer, let alone a rolling boil. If I cover the container at this steady state, it reaches a rolling boil in about another 90s.
- The concrete example seems just an example of scope insensitivity?
- I don't trust the analysis of point (2) in the concrete example. It seems plausible turning off the wifi has a bunch of second-order effects, like making various wifi-connected devices not to run various computations happening when online. Consumption of the router could be smaller part of the effect. It's also quite possible this is not the case, but it's hard to say without experiments.
- I would guess most aspiring rationalists are prone to something like an "inverse salt in pasta water fallacy": doing a Fermi estimate like the one described, concluding that everyone is stupid, and stopping to add salt to pasta water.
- but actually people add salt to pasta water because of the taste
- it's plausible salt actually decreases cooking time (or increases cooking time) - but the dominant effect will be chemical interaction with the food. Salt makes some food easier to cook or harder to cook
- overall, focusing on proving something about the non-dominant effect ... is not great
the second-order effects of turning off the WiFi are surely comprised of both positive and negative effects, and i have no idea which valence it nets out to.
these days homes contain devices whose interconnectedness is used to more efficiently regulate power use. for example, the classic utility-controlled water heater, which reduces power draw when electricity is more expensive for the utility company (i.e. when peakers would need to come online). water heaters mostly don’t use WiFi but thermostats like Nest, programmable light bulbs, etc do: when you disrupt that connection, in which direction is power use more likely to change?
i have my phone programmed so that when i go to bed (put it in the “i’m sleeping” Do Not Disturb mode) it will automatically turn off all the outlets and devices — like my TV, game consoles, garage space heater — which i only use during the day. leaving any one of these on for just one night would cancel weeks of gains from disabling WiFi.
the second-order effects of turning off the WiFi are surely comprised of both positive and negative effects
Linguistic nitpick: Strictly speaking the effects comprise both positive and negative effects. Equivalently, the effects are composed of both positive and negative effects.
The whole comprises the parts. The parts compose the whole.
I’m actually more interested in reverse salted pasta water fallacies! It’s an extension of Chesterton’s Fence, but with an added twist where the fence has a sign with an incorrect explanation of what the fence is for.
In the language of Bayes, we might think of it thus:
E = The purpose of the fence stated on the sign H = The actual purpose of the fence is the stated one
The fallacy would simply be ascribing too high a prior value of P(H), at least within a certain reference class.
Potentially, that might be caused by rationalists tailoring their environment such that a high P(H) is a reasonable default assumption almost all the time in their lived experience. Think a bunch of SWE autistics who hang out with each other and form a culture centered on promoting literal precise statements. For them, P(H) is very high for the signs they’ll typically encounter.
The failure mode is not noticing when you’re outside the samples distribution of life circumstances - when you’re thinking about the world outside rationalist culture. It may not have a lower truth content, but it may have lower literalism. But there’s not always a clear division between them, and anyway, insisting on literalism and interrogating the false premises of mainstream culture is a way of expanding the boundaries of rationalist culture.
Also you would have to add back in additional time to get the water to its (new, higher) boiling point in the first place...
Though, actually, apparently adding salt decreases the "specific heat capacity" of water, so that increasing it by N degrees requires less heat to be added (and therefore takes less stove time). The numbers in this article suggest that this makes a larger difference than the increased boiling point would.
(Though, again, the effect size seems to be epsilon for realistic amounts of salt people would add.)
The article has an egregious typo where they say “The pot containing a 20% salt concentration will heat up over 25 times faster”. I think they meant “over 25% faster”, which is either true or close-to-true. I’m not sure about the conclusion that cooking time goes (slightly) down; I think they’re holding total-mass fixed, but if we’re talking about “adding salt” then we should hold water-mass fixed instead, which adds onto the boiling point elevation effect and might tip the balance. I didn’t do the calculation because it’s entirely pointless. :-P
Doing the math because I have the urge:
- The graphs look like straight lines within the range from 0-5% salt concentration, so I'll use the numbers at 5% and assume they scale down to the epsilon of salt one would actually add.
- Density appears to increase by 4%.
- Specific heat appears to go from 4200 to 3930 (edit: not 3850, whoops), a decrease of ~7%.
- Boiling point ... not present in your link, but this says approximately +0.5° C per 2.9% of salt, so let's say at 5% salt it becomes 100.8°C. The delta from a starting point of, say, 21°C thus increases by about 1%.
- Conclusion: time to boiling is multiplied by , a (tiny) decrease.
- Addendum: I see recommendations of 1 tablespoon of salt per gallon of water, which is 0.4% by mass, so in practice the time to boiling would be multiplied by more like 0.998.
I think you meant 3950 not 3850? And if we hold water-mass fixed instead of total-volume (i.e. the water is already in the pot and we’re deciding whether to add salt or not) we should use 5% not 4% (density doesn’t matter, because we don’t care whether the volume goes up a bit upon adding salt). Seems awfully close to even.
(I don't know much about physics, but...) Raising the boiling point just means raising the maximal temperature of the water. Since during normal (saltless) cooking that maximum is usually reached at some time x before the pasta is done, raising the boiling point with salt means the water becomes overall hotter after x, which means you have to cook (a tiny bit) shorter. What makes the pasta done is not the boiling, just the temperature of the water and the time it has some temperature.
Im pretty sure, though I cannot find data on it, that cooking in salt water simply causes salt to interact chemically with the pasta, "tenderizing" it, the same way salt tenderizes meat, vegetables etc.
I assume we could perform an experiment in which we submerge identical amounts of pasta in cold tap water, and in an equal volume of salt water, and wait until it becomes soft enough to eat. My assumption is that waterlogging pasta in salt water would soften it much faster.
Right, but if you wait for the water to boil before you put the pasta in, then you are waiting a little longer before adding the pasta. Then cooking the pasta slightly shorter after you put it in.
Yeah. And many people do indeed recommend one should add pasta only after the water is boiling. For example:
Don't add the noodles until the water has come to a rolling boil, or they'll end up getting soggy and mushy.
Except ... they don't get soggy.
I would know, I made a lot of pasta in spring of 2020!
While we're at it, they also say
Bring a large pot of water to a boil.
which other sources also tend to recommend. This is usually justified by saying that by using a lot of water the pasta will thereby stick together less. But as I said, I consider myself a noodle expert now, I optimized the process, and using a larger pot just increases the cooking time (since more water takes longer to get hot), but has no measurable influence on stickiness.
There have been multiple egregious examples of this fallacy with respect to pandemic policy. The complete lack of rational cost benefit analysis (across the political spectrum) for the various measures was truly disheartening.
But to give a less politically charged example: Locally, in response to drought conditions, some restaurants announced they would only bring glasses of water to the table, on request. Now, this might make some sense in terms of reducing labor, although the extra work of having to ask everyone, and possibly bring out additional glasses later, probably cancels this out. But for reducing water usage, this is just silly. Let's do some math:
Total water usage in US is about 1000 gal/person-day (including domestic, agricultural and industrial uses). So, assuming 50% of patrons leave their 12 oz glass of water untouched, you are reducing the daily water consumption of restaurant patrons by less than 0.005%. Of course, it also takes water to wash said glass -- it can vary a lot, but 18 oz of water would be a reasonable estimate (assuming an automatic commercial dishwater). That gets us up around 0.012%, or the water you get from running the faucet in the sink for 5-10 seconds.
The complete lack of rational cost benefit analysis (across the political spectrum) for the various measures was truly disheartening.
To be fair there also was an environment of high uncertainty in which making good CBA without data was simply impossible, and calling for extensive and unrealistic standards of proof was a common dithering technique from people who simply didn't want anything done on principle. We still lack good enough data on transmission properties to e.g. estimate properly the benefits of ventilation in reducing it, three years into this. I was honestly baffled that the first thing done in March 2020 wasn't to immediately estimate in multiple experiments how long the virus stayed in the air or on surfaces still viable, how much exposure caused infection, etc. We had like a couple of papers at best, and not very good ones, apparently because it was hard to do the experiments and they required a P4 lab or so. Meanwhile the same researchers would probably encounter the virus daily at the grocer.
It's hard to get good data, yes, particularly in a politically charged environment. But, I would have liked to have seen some evidence that for a given mitigation, our leaders tried to get a best estimate (even if it is not a great estimate) that it will prevent X COVID deaths, at a cost of Y (dollars, QALYs, whatever), and had done some reasoning why utility(X) > cost(Y). We might disagree on the values of X and Y, and how to compare them, but at least we would have a starting point for discussion. Instead, we got either "Don't take away muh freedom!" or "We must stop anyone from dying of COVID at all costs!". And a lot of people died, and we inflicted tremendous damage on ourselves, while doing some things that were maybe beneficial, and a lot of things that were clearly stupid, and we're not in a position to do better next time.
I think the problem here is also forced choices, which were in themselves loaded on purpose. If I tell you the two choices are "let COVID spread unimpeded" or "lock down without any support mechanism so that the economy crashes so hard it kills more people than COVID would" (honestly I don't think we actually fared that bad in western countries though, pre-vaccine COVID really would have killed a fuckton of people if it got in full swing), then I'm already loading the choice. Many politicians did this because essentially they were so pissy about having to do something that ran counter to their ideological inclinations that they took a particular petty pleasure in doing it as badly as they could, just to drive home that it was bad. This is standard "we believe the State is bad, that is why we will get in charge of the State and then manage it like utter fuckwits to demonstrate that the State is bad" right wing libertarian-ish behaviour. Boris Johnson and the British Tories in particular are regularly culpable of this, and were so during the pandemic as well.
A third, saner option would have been "close schools, make it legally mandated for every employer who can allow work from home to make their people work from home, implement these and those security measures for those who otherwise can't, close businesses like restaurants and cinemas temporarily, then tax (still temporarily!) the increased earnings of those citizens and companies who are less affected by these measures to pay for supporting those businesses and people that are more affected so that the former don't go bankrupt, and the latter don't starve". You know, an actual coordinated action that aims at both minimizing and spreading fairly the (inevitable) suffering that comes with being in a pandemic. Do that on and off while developing testing and tracing capacity as well as all sorts of mitigation measures, and until a vaccine is ready. Then try to phase out to a less emergency mode, more sustained regime that however still manages infection rates and their human and economic costs seriously.
We... really didn't get that. But the original sin was IMO mainly in the way pandemic plans were already laden with ideology from the get go. The whole "let it rip" thing the UK tried before desperately backtracking? That WAS our official pandemic plan. Designed for flu rather than a coronavirus with twice the R0, admittedly, but still. The best idea they could come up with was "do nothing, but pretend it's on purpose to look more clever", essentially, because everything else felt inadmissible as it impinged on this or that interest or assumption that couldn't possibly be broken. As it turns out, the one thing that plan underestimated, for all its pretences of being a masterpiece of grounded realpolitik, was the pressure from people not wanting to get sick or die. Who could have guessed. As such, the backlash and following measures like lockdowns were implemented in a rush and thus very poorly and without real plans or coordination. Might have helped to see that coming first.
Light bulbs, phones and laptops consume ≈0 energy. Don't skimp on them.
Edit: more precisely- cost of 1 hour of working of:
A light bulbs≈ $0.01/hour and ten time less for an energy-saving one
A phone≈ $0.0017
A laptop≈ $0.01
1The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2024. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
Interesting post. As a counterpoint, a famous cycling coach in the UK spent a lot of time talking about "marginal gains". Essentially the exact opposite philosophy, chasing down all of the tiny improvements. (Random article I found on it: https://jamesclear.com/marginal-gains , although it kind of goes off course at the end into self help stuff.)
Aside, I always assumed the salt in pasta water was for some kind of osmosis thing. My vague reasoning was that water can diffuse in or out of the pasta and the concentration of non-water things (like salt or starch) on the inside vs. outside will control how much the water 'likes' one side of the barrier or not.
Something like your 3% improvement is another example of epsilon gains working.and perhaps your Realistic expectations for disagreement fit here.
Important Note: you have been misled about salted pasta water and what chefs claim it does (though home cooks do in fact usually get this wrong).
A sophisticated chef will say the salt is added to increase the boiling point of the water so that the noodles can be cooked hotter for a shorter period of time.
This is incorrect (for the reasons you noted in the post). The salt does not actually move the boiling point by enough to be useful. Instead, the salt itself helps change the pasta to have an "al dente" texture.
Conclusion:
The fallacy, I claim, is that 2.6s are nothing. Adding salt does not decrease cooking time. It doesn't increase it either, it just does nothing (wrt cooking time at least). [emphasis added]
This is the very first example of "The salt in pasta water fallacy" fallacy — a difference being ignored because it seemed irrelevant. In the original post's examples, people ignored small differences, imagining them irrelevant, but in the original post's text, someone ignored a difference because it seemed irrelevant.
Salt your pasta water! Don't salt it! Try both!
Nit: I think the energy savings from turning off your wifi will be higher, as your ISP also saves on not having to run some routers and so on
Another factor to consider when asking whether 'salt reduces cooking time': Presumably, if the boiling temperature is higher, there will be some extra amount of time needed to raise the water temp that much. So your 2.6 seconds becomes (2.6s - extraPreBoilingTime). It's feasible even that this turns your value negative. That, combined with the amount of time needed to grab the salt, and clean up any spilled salt (lets say 1 in 5 times) almost certainly ends up with you losing time, on average.
So your friend isn't even technically correct. Bob is wrong on both counts.
I'd advise dumping him as a friend. Save your starchy water though.
As you've described it, the fallacy is fairly harmless (it doesn't materially speed up cooking pasta, but it also doesn't slow it down). The only thing lost is a bit of time that could be more productively spent doing something else. I think there's often a side effect which goes along with this fallacy that's worth mentioning, and can turn it into something actively harmful.
With the example of trying to save energy by turning off the wifi router, a proportion of people will turn the wifi off but not turn the heating down because they think "I followed one of the recommendations, I'm making an effort and doing my part". Adding in the recommendation to turn off the wifi can be actively harmful because people don't even necessarily understand that some of the recommendations are more impactful than others, and they're working off a model of social status signalling to determine what actions they should take, rather than actually understanding the problem and how the proposed solutions are intended to help.
Recycling is a similar situation. Most waste which goes into recycling is not actually recycled, but the act of recycling makes people believe that they are fulfilling their civic duty to reduce single use plastics and wasteful use of resources. As a result they may shirk other much more effective and important green initiatives.
(as a sidenote, energy which is used by the wifi router is going to be disappated as heat, so turning off the wifi will just mean that your heating system will just work a little harder to reach the temperature set by the thermostat, offsetting any savings made by turning the wifi off.)
I wonder whether stuff like "turn off the wifi" is about costly signals? (My first-order opinion is still that it's dumb.)
Recent research has stated that the most effective way to save energy while cooking pasta is to simply turn off the stove once the pasta is in water. The rest heat will cook the pasta without a problem, cooking time is approximately the same, but you can save about 1/2 energy!
I am 60 yrs old and I have never heard it claimed that salt reduces the time it takes to cook pasta. However, I have observed that it does bring the water to a boil faster, which reduces overall cooking time.
I love this kind of post which gives a name to a specific behavior and also gives good examples for identifying it. They feel very validating for noticing the same fallacy that annoys me, but which I encounter so infrequently that it's hard to notice any pattern and articulate what feels wrong about it.
This is a good example of neglecting magnitudes of effects. I think in this case most people just don't know the magnitude, and wouldn't really defend their answer in this way. It's worth considering why people sometimes do continue to emphasize that an effect is not literally zero, even when it is effectively zero on the relevant scale.
I think it's particularly common with risks. And the reason is that when someone doesn't want you to do something, but doesn't think their real reason will convince you, they often tell you it's risky. Sometimes this gives them a motive to repeat superstitions. But sometimes, they report real but small risks.
For example, consider Matthew Yglesias on the harms of marijuana:
Inhaling smoke into your lungs is, pretty obviously, not a healthy activity. But beyond that, when Ally Memedovich, Laura E. Dowsett, Eldon Spackman, Tom Noseworthy, and Fiona Clement put together a meta-analysis to advise the Canadian government, they found evidence across studies of “increased risk of stroke and testicular cancer, brain changes that could affect learning and memory, and a particularly consistent link between cannabis use and mental illnesses involving psychosis.”
I'll ignore the associations with mental illness, which are known to be the result of confounding, although this is itself an interesting category of fake risks. For example a mother that doesn't want her child to get a tattoo, because poor people get tattoos, could likely find a correlation with poverty, or with any of the bad outcomes associated with poverty.
Let's focus on testicular cancer, and assume for the moment that this one is not some kind of confounding, but is actually caused by smoking marijuana. The magnitude of the association:
The strongest association was found for non-seminoma development – for example, those using cannabis on at least a weekly basis had two and a half times greater odds of developing a non-seminoma TGCT compared those who never used cannabis (OR: 2.59, 95 % CI 1.60–4.19). We found inconclusive evidence regarding the relationship between cannabis use and the development of seminoma tumours.
What we really want is a relative risk (how much more likely is testicular cancer among smokers?) but for a rare outcome like testicular cancer, the odds ratio should approximate that. And testicular cancer is rare:
Testicular cancer is not common: about 1 of every 250 males will develop testicular cancer at some point during their lifetime.
So while doubling your testicular cancer risk sounds bad, doubling a small risk results in a small risk. I have called this a "homeopathic" increase, which is perhaps unfair; I should probably reserve that for probabilities on the order of homeopathic concentrations.
But it does seem to me to be psychologically like homeopathy. All that matters is to establish that a risk is present, it doesn't particularly matter its size.
Although this risk is not nothing... it's small but perhaps not negligible.
This fallacy occurs when a claim is made (adding salt will reduce cooking time, turning off the wifi will save energy), that is both true, and negligible. The claim may convince one to do something (add salt, turn off the wifi), even though the advice is completely useless. This is a fallacy because the person making the claim can always argue that "The claim is true", in some logical sense, while the person receiving the advice is mislead to believe that is "The claim is relevant". It is difficult to fight the person making the claim, because they could always shift the debate toward the truth of the claim.
Why 'fight the person making the claim'?
Just saying "that's true but not relevant" seems fine enough to move on?
I think its not really related.
OP's point: "Turning off my router at night will make a positive difference, but one too miniscule to matter."
Wiki's point: "Saying that a typical household would save 27.03467 pence per year by turning off the router at night is silly. Just round to 25 or 30 pence."
Curated and popular this week